Introduction

Non-Hermitian (NH) Hamiltonians provide conceptually simple, intuitive, and powerful descriptions of a wide range of systems1, such as wave systems with loss/gain2,3,4, and open systems5,6,7. Diverse intriguing phenomena in NH systems, such as exceptional points (EPs)3,8,9,10, have spurred extensive research and found numerous applications across various fields11,12,13,14.

The bulk-boundary correspondence (BBC) that predicts, for example, the existence and the number of chiral edge modes by the bulk Chern number is at the core of the topological band theory15. The BBC implicitly assumes that the Hamiltonians with open boundary condition (OBC) share essentially the same bulk eigenvalue spectra with their counterparts with periodic boundary condition (PBC). The assumption no longer holds in some NH systems that exhibit non-Hermitian skin effect (NHSE)16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38, which manifests as the pileup of macroscopically many eigenstates at the system boundaries under OBC and the consequent difference between OBC and PBC systems in their spectra16. As a result, the conventional BBC needs to be rectified.

Some remedies have been proposed to resolve the problem, among which two approaches known as the non-Bloch approach16,39,40,41 and the biorthogonal approach42 are most popular and illuminating. The non-Bloch approach has been applied successfully in many systems16,40,41. By extending the concept of Brillouin zone (BZ) to generalized Brillouin zone (GBZ), a substitute Hamiltonian known as the non-Bloch Hamiltonian is constructed to serve as the bulk to define a topological invariant. The non-Bloch approach correctly predicts the existence of topological edge states and captures topological transitions. Its basic idea is to find a proper Hamiltonian that is devoid of NHSE and has identical OBC spectrum with the original system. The biorthogonal approach uses both the left and right eigenvectors to determine topological transitions and distinguish between edge states and bulk states, which are difficult to distinguish due to NHSE42.

Here we propose a different approach which is more physically intuitive, transparent, and notably less involved compared to the non-Bloch approach. For illustration, we consider the NH Su-Schrieffer-Heeger (SSH) model with asymmetric intracell hoppings16. We adopt a double-sized unit cell comprising two primitive unit cells and swap the asymmetric intracell hoppings in every second primitive unit cell. This arrangement, which we call doubling and swapping, counterbalances the asymmetry and removes NHSE in the modified system. Importantly, we find that the doubling and swapping does not change the OBC spectrum compared to the original NH SSH chain. Therefore the modified system can serve as the faithful bulk for defining topological invariants that correctly predicts edge states and topological phase transitions. The outcome is the same as that of the non-Bloch approach but our approach is more straightforward and physically transparent: There is no need to figure out the GBZ and the only cost is involving more bands. The doubling and swapping method relies on a parameter-swapping symmetry observed in some non-Hermitian systems, which ensures that the characteristic polynomial of the OBC Hamiltonian remains invariant even when these parameters are interchanged, for example, the two asymmetric intracell hopping parameters in the NH SSH model with nearest-neighbor hoppings exhibit this symmetry. This method is not applicable to all non-Hermitian systems with NHSE, however, it is highly effective in handling the most pertinent ones and can successfully capture the essential aspects of the problem. We point out that the approach is also applicable to many other systems such as the NH Creutz ladder with gain/loss43. Furthermore, we extend the study to disordered systems in which the asymmetric hoppings are randomly swapped. We find that two types of winding numbers can also be defined in the disordered systems to account for the presence of NHSE and topological edge states, respectively.

Results

BBC restored by doubling and swapping method

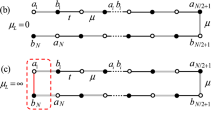
We consider the NH SSH model with asymmetric intracell hoppings t1, t2 and intercell hopping s shown in Fig. 1a. The dashed box marks a double-sized unit cell consisting of two primitive unit cells, which corresponds to the four-band Bloch Hamiltonian

$$H(k)=\left(\begin{array}{cccc}0&{t}_{1}&0&s{e}^{-ika}\\ {t}_{2}&0&s&0\\ 0&s&0&{t}_{1}\\ s{e}^{ika}&0&{t}_{2}&0\end{array}\right),$$
(1)

where a = 2a0 with a0 being the primitive lattice constant. It is well known that, due to NHSE, H(k) is not a faithful bulk to capture the topological edge states16.

Fig. 1: Topological transition captured by the swapped model.
figure 1

a The supercell structure of the non-Hermitian (NH) Su-Schrieffer-Heeger model (SSH) H(k). b The modified system \({H}^{{\prime} }(k)\) obtained from (a) by swapping the non-reciprocal hoppings t1, t2 in every second unit cell. c, d The band structures of (a) and (b). \({{{{{{\mathrm{Re}}}}}}}\,(E)\) and \({{{{{{\mathrm{Im}}}}}}}\,(E)\) bands are represented by solid and dashed lines, respectively. Parameters s = 1, t1,2 = t ± γ/2 with t = 1/2, γ = 4/3 are used. Four \({{{{{{\mathrm{Re}}}}}}}\,(E)\) bands pairwise coincide in (d), and for visual clarity they are intentionally drawn to be slightly separated. e The topological transitions occur at \(t=\pm {t}_{c}=\pm \sqrt{{s}^{2}+{(\gamma /2)}^{2}}\) as evidenced in the variation of winding number w as t changes. The blue dots and dashed line represent numerical and theoretical results, respectively. t = ± tEP = ± 2/3 denote transition points between regions with complex-valued bands (∣t∣ < tEP) and regions with real-valued bands (∣t∣ > tEP). f Bandgap of \({H}^{{\prime} }(k)\) closes at the topological transition point t = tc ≈ 1.2.

Full size image

To counterbalance the NHSE, we swap the non-reciprocal hoppings t1, t2 in every second primitive cell and get a modified chain configuration as shown in Fig. 1b, which corresponds to a modified four-band Bloch Hamiltonian,

$${H}^{{\prime} }(k)=\left(\begin{array}{cccc}0&{t}_{1}&0&s{e}^{-ika}\\ {t}_{2}&0&s&0\\ 0&s&0&{t}_{2}\\ s{e}^{ika}&0&{t}_{1}&0\end{array}\right).$$
(2)

It is obvious that the presence of inversion symmetry in Fig. 1b suppresses the NHSE44. We note that the doubling and swapping method differs in both construction methods and objectives from the Hermitianization procedure used in45 and46, which converts the NH SSH chain in Fig. 1a to two separate Hermitian chains (instead of a single NH chain) and treats the topology of a non-trivial point gap (instead of a line gap). Specifically, for a non-Hermitian system under OBC in the thermodynamic limit,45 and46 respectively relate the topological characterization of its skin modes and zero singular modes to the topological characterization of the zero eigenmodes in the enlarged Hermitian system.

For convenience, we refer to the OBC counterparts of H(k) and \({H}^{{\prime} }(k)\) as Hobc and \({H}_{obc}^{{\prime} }\), respectively. Just like Hermitian Hamiltonians, \({H}^{{\prime} }(k)\) can be used to establish the BBC to predict the topological edge states in \({H}_{obc}^{{\prime} }\), due to the absence of NHSE. As tridiagonal matrices representing chains with nearest-neighbor hoppings, Hobc and \({H}_{obc}^{{\prime} }\) have identical spectrum, since the spectrum depends solely on the product of t1 and t2 rather than on each value singly (see Methods). And they are generally equivalent under a similarity transformation, except in certain rare scenario where EPs are involved and Hobc and \({H}_{obc}^{{\prime} }\) have distinct Jordan normal forms (see Methods). This implies that the NHSE-free system \({H}^{{\prime} }(k)\) can serve as a valid bulk system for predicting edge states and topological transitions in Hobc as well.

While the systems depicted by Fig. 1a, b have the same eigenvalues under OBC, the band structures of H(k) and \({H}^{{\prime} }(k)\) under PBC exhibit a clear contrast, as shown in Fig. 1c, d, where solid and dashed curves denote \({{{{{{\mathrm{Re}}}}}}}\,E(k)\) and \({{{{{{\mathrm{Im}}}}}}}\,E(k)\) bands, respectively, for the specific set of parameters s = 1, t1,2 = t ± γ/2 with t = 1/2, γ = 4/3. The solid bands in Fig. 1d should actually coincide pairwise, and are intentionally slightly offset for better visibility. Unlike Hermitian scenarios, Fig. 1c exhibits an unexpected absence of BZ-folding-induced degeneracies (i.e., \({{{{{{\mathrm{Re}}}}}}}\,{E}_{i}={{{{{{\mathrm{Re}}}}}}}\,{E}_{j}\) accompanied by \({{{{{{\mathrm{Im}}}}}}}\,{E}_{i} \, \ne \, {{{{{{\mathrm{Im}}}}}}}\,{E}_{j}\) at k = ± π/a) due to NHSE (see Supplementary Note 1 for more details).

Due to the chiral symmetry, \({H}^{{\prime} }(k)\) can be flattened to an off-diagonal Q matrix, namely \(Q(k)={\mathbb{I}}-2P(k)=\left[\begin{array}{cc}0&q(k)\\ {q}^{-1}(k)&0\end{array}\right]\), where \(P(k)={\sum }_{n = 1,2}\left\vert {\psi }_{n}^{R}(k)\right\rangle \left\langle {\psi }_{n}^{L}(k)\right\vert\) with \({\psi }_{n}^{R/L}\) denoting right/left eigenvectors of \({H}^{{\prime} }(k)\)16. The two-band winding number16,47,48,

$$w=\frac{1}{2\pi i}{\int}_{BZ}Tr\left[{q}^{-1}(k){\partial }_{k}q(k)\right]dk,$$
(3)

can be employed to capture the existence of topological edge states in Hobc. Alternatively we can use the two-band Berry phase to characterize the topology utilizing the inversion symmetry in \({H}^{{\prime} }(k)\) (see Methods).

Figure 1e shows the variation of the winding number w with respect to t, with the numerical and theoretical results represented by blue dots and a dashed line, respectively. The topological transitions occur at \(t=\pm {t}_{c}=\pm \sqrt{{s}^{2}+{(\gamma /2)}^{2}}\), which is derived from s2 = t1t2 and agrees with the non-Bloch approach result16. \({H}^{{\prime} }(k)\) becomes gapless at t = tc, as is shown in Fig. 1f.

An EP transition occurs at t = ± tEP = ± γ/2, where the \({H}^{{\prime} }(k)\) bands transition from complex-valued to real-valued for ∣t∣ > tEP (i.e., t1t2 > 0). tEP is marked in Fig. 1e. When t = ± tEP, a pair of two-fold flat bands with E = ± s occur, with EPs for k ∈ (− π/a, π/a) and nondefective degeneracies at k = ± π/a (see Supplementary Note 2).

Following similar reasoning in obtaining \({H}^{{\prime} }(k)\), we can construct a two-band NHSE-free system,

$${h}^{{\prime} }(k)=\left(\begin{array}{cc}0&\tau +s{e}^{-ik{a}_{0}}\\ \tau +s{e}^{ik{a}_{0}}&0\end{array}\right),$$
(4)

by replacing the asymmetric hoppings t1 and t2 in the original two-band system h(k) (see Fig. 1a) with \(\tau =\sqrt{{t}_{1}{t}_{2}}\)16,44. Equation (4) can also serve as the bulk, since its OBC counterpart shares the same spectrum with Hobc, which only depends on the product of t1 and t2, and not on each value separately. We note that \(\tau =i\sqrt{| {t}_{1}{t}_{2}| }\) and \({h}^{{\prime} }(k)\) is NH when t1t2 < 0, and it is Hermitian when t1t2 > 0. It is evident from Eq. (4) that the nontrivial region ∣t∣ < tc depicted in Fig. 1e can be inferred from ∣τ∣ < s, meaning that the intracell hopping in \({h}^{{\prime} }(k)\) is weaker than the intercell hopping. We note that when t1 > t2 > 0, \({h}^{{\prime} }(k)\) has the same form as the non-Bloch Hamiltonian HnB(k) (see Methods). Moreover, by BZ-folding the \({h}^{{\prime} }(k)\) bands, we can obtain the \({H}^{{\prime} }(k)\) bands in Fig. 1d (see Supplementary Note 3).

Compared to the non-Bloch approach, the doubling and swapping method is more intuitive, transparent, and less involved. It has the advantage of enabling efficient computation of the continuous OBC spectrum of a large system, without the need for diagonalizing a large OBC Hamiltonian matrix which is especially challenging due to NHSE.

As for the presence of NHSE, a different winding number based on eigenvalues18,19,45,49

$$\nu ({E}_{b})=\frac{1}{2\pi i}\int\nolimits_{0}^{2\pi }\frac{d}{dk}\ln \det \left[H(k)-{E}_{b}\right]dk,$$
(5)

can be used to characterize it, where Eb denotes any point in the complex energy plane. Skin modes appear under OBC if and only if there exists \({E}_{b}\in {\mathbb{C}}\) with respect to which the PBC spectrum denoted as σ[H(k)] has nonzero winding, i.e., ν ≠ 0. In other words, a point gap in σ[H(k)] is associated with the NHSE18. To differentiate from Eq. (3), we call the eigenvalue-based ν(Eb) as the spectral winding number, and call the eigenvector-based w as the chiral winding number. Such spectral winding number will also be useful for describing random systems as we will see below.

Random swapping

A natural query arises: what happens if the swapping is conducted randomly? We randomly swap the asymmetric hoppings t1,  t2 in an SSH chain, assigning an equal probability of 1/2 for either swapping or taking no action, so that the NHSE should be eliminated on average; and investigate how topology, NHSE and disorder interplay. We connect a disordered chain \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) end-to-end to get its ring counterpart \({{{{{{{{\mathcal{H}}}}}}}}}_{r}\). We denote the spectra of \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) and \({{{{{{{{\mathcal{H}}}}}}}}}_{r}\) by \(\sigma [{{{{{{{{\mathcal{H}}}}}}}}}_{r}]\) and \(\sigma [{{{{{{{{\mathcal{H}}}}}}}}}_{c}]\).

We observe that, akin to σ[H(k)], \(\sigma [{{{{{{{{\mathcal{H}}}}}}}}}_{r}]\) typically manifest as loops in the complex energy plane, which wind around the arcs of \(\sigma [{{{{{{{{\mathcal{H}}}}}}}}}_{c}]\). An example is shown in Fig. 2a, where the spectra of three different L = 80\({{{{{{{{\mathcal{H}}}}}}}}}_{r}\) configurations (i.e., comprising 80 sites) we pick are denoted by orange, green and red dots, respectively. The three corresponding \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) systems share a common spectrum as denoted by blue crosses in Fig. 2a, which includes two edge states at E ≈ 0. The enclosing behavior in Fig. 2a implies remnant NHSE and the size of enclosed area signifies the strength of the NHSE which varies for different random configurations. For comparison, σ[H(k)] is shown by the dashed circle enclosing a much bigger area, indicating much stronger NHSE under OBC than the disordered rings. The results indicate that, for random configurations, the NHSE is predominantly eliminated. However, remnants of it still persist, and the intensity of these remnants varies depending on the configuration. We can view \({H}^{{\prime} }(k)\) as a special case of the random configurations that is NHSE-free, and its spectrum \(\sigma [{H}^{{\prime} }(k)]\) encloses exactly zero area.

Fig. 2: Topological characterization of skin effect in the presence of random swapping.
figure 2

a The spectra for three different L = 80 random ring configurations \({{{{{{{{\mathcal{H}}}}}}}}}_{r}\) (orange, green, red), common spectrum for three chain configurations \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) (blue crossings), and H(k)’s spectrum (gray dashed). Parameters \(s = 1, t_{1,2} = t \pm \gamma / 2 \, {{{\rm{with}}}} \, t = 1/2, \gamma = 4/3\) are used. b, c Three arbitrarily chosen wavefunctions ∣ψ(x)∣ of the 3rd configuration for \({{{{{{{{\mathcal{H}}}}}}}}}_{r}\) and \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\), respectively. d Depiction of winding number \({\nu }^{{\prime} }(E)\) in Eq. (6) regarding non-Hermitian skin effect: spectral winding (two loops) induced by increasing flux Φ from 0 to 2π in a L = 20 random ring configuration.

Full size image

For illustration, three arbitrarily chosen wavefunctions of \({{{{{{{{\mathcal{H}}}}}}}}}_{r}\) and its chain counterpart \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) are shown in Fig. 2b, c, respectively, for the third configuration corresponding to the red dots in Fig. 2a. With the ring cut open, wavefunctions accumulate to the right boundary as is shown in Fig. 2c, indicating the existence of NHSE under swapping disorder in a finite-size chain. Different random chains are related by similarity transformations (except in certain rare cases involving EPs), as is the case for Hobc and \({H}_{obc}^{{\prime} }\).

Similar to Eq. (5), a winding number associated with the winding of \(\sigma [{{{{{{{{\mathcal{H}}}}}}}}}_{r}]\) around \(\sigma [{{{{{{{{\mathcal{H}}}}}}}}}_{c}]\) as shown in Fig. 2a can be used to characterize the NHSE45,50:

$${\nu }^{{\prime} }({E}_{b})=\frac{1}{2\pi i}\int\nolimits_{0}^{2\pi }\frac{d}{d\Phi }\ln \det \left[{{{{{{{{\mathcal{H}}}}}}}}}_{r}(\Phi )-{E}_{b}\right]d\Phi ,$$
(6)

where Φ denotes the flux that threads the \({{{{{{{{\mathcal{H}}}}}}}}}_{r}\) ring. Equation (6) reduces to Eq. (5) when disorder is absent45. The flux Φ appears as phase factors e±iΦ/L multiplied to hoppings according to the Peierls substitution51. Taking a L = 20 random ring for example, the winding of \(\sigma [{{{{{{{{\mathcal{H}}}}}}}}}_{r}(\Phi )]\) with respect to Φ is shown in Fig. 2d, where five sets of spectra are displayed in different colors and the arrows indicate the directions of spectral winding. The random chain’s spectrum \(\sigma [{{{{{{{{\mathcal{H}}}}}}}}}_{c}]\) is shown by blue crossings, which is enclosed by \(\sigma [{{{{{{{{\mathcal{H}}}}}}}}}_{r}(\Phi )]\).

Different random chains have identical spectrum and their topological edge states all occur around E = 0 and are generally related by similarity transformations. Their common topological transitions and topological edge states can be captured by the winding number w in Eq. (3) defined based on \({H}^{{\prime} }(k)\). Alternatively, the winding number for the random chains can also be computed using the real-space formula52,53:

$${w}^{{\prime} }=\frac{1}{{L}^{{\prime} }}T{r}^{{\prime} }(SQ[Q,X]),$$
(7)

where S = diag{1, − 1, 1, − 1, … } is the chiral symmetry operator, X = diag{1, 1, 2, 2, … } denotes the coordinate operator, and Q is the flattened version of \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\), and \(T{r}^{{\prime} }\) denotes the trace over the middle interval x ∈ [ℓ + 1, L − ℓ] of the chain. In practice, a modest chain size is sufficient. The variation of \({w}^{{\prime} }\) with t is shown in Fig. 3a, which is the same as Fig. 1e except that the latter has the merit of being immune to finite-size errors. The value of \({w}^{{\prime} }\) remains unchanged when we alter the random configuration of \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\), which is a noteworthy result (see proof in Methods).

Fig. 3: Topological edge states in the presence of random swapping.
figure 3

a Winding number \({w}^{{\prime} }\) of a L = 80 random chain calculated using Eq. (7). The dots and dashed line represent numerical and theoretical results, respectively. b The two topologically protected E = 0 states (real part) are denoted by blue and orange lines. The inset shows their imaginary parts.

Full size image

\({w}^{{\prime} }\ne 0\) predicts the existence of a pair of E ≈ 0 states ψ1, ψ2 in a random chain \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\), which are generally edge states localized at the left or right edge (depending on the configuration), noting that NHSE-induced delocalization of edge states is a rare event54,55. For illustration, the edge states ψ1 and ψ2 for the third random \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) configuration are shown in Fig. 3b. They are related by chiral symmetry, i.e., ψ1 = Sψ2. The edge states of \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) are generally connected to those of \({H}_{obc}^{{\prime} }\) through a similarity transformation, which embodies the NHSE in \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\): It amplifies (attenuates) the right (left) side of the edge states of \({H}_{obc}^{{\prime} }\) that are localized at both edges and exhibit even/odd parity due to inversion symmetry, resulting in ψ1, ψ2 in Fig. 3b that are similar. When the size of Hobc goes to infinity, its two edge states tend to form an EP due to NHSE43 (see Supplementary Note 4).

Application to other systems

The doubling and swapping method to restore the BBC can be extended straightforwardly to other systems that exhibit NHSE including higher-dimensional ones. For example, the BBC in the NH Creutz ladder model shown in Fig. 4a can be restored by using a modified bulk obtained by swapping gain/loss in every second primitive cell43. This is anticipated since swapping gain/loss ± iγ/2 in Fig. 4a is equivalent to swapping the non-reciprocal hoppings t ± γ/2 in Fig. 1a (see Methods). We find that, for every randomly swapped NH Creutz ladder, there exists a randomly swapped SSH chain related to it by a similarity transformation (see Methods). Consequently, similar results as shown in Figs. 2 and 3 occur to the NH Creutz ladder in the presence of random swapping. In Fig. 4b, c, we present two NH SSH models with next-nearest-neighbor hoppings that can be treated using the swapping method to obtain their true bulk Hamiltonians. Although the models do not have chiral symmetry, the swapping method is still effective in determining the boundaries between different gapped phases under OBC. Our method is also applicable to two dimensional (2D) systems like 2D NH SSH shown in Fig. 4d and NH Benalcazar-Bernevig-Hughes (BBH) model56 in Fig. 4e, which contain asymmetric hoppings in both directions. We provide a detailed demonstration of the applicability of the swapping method to the NH BBH model in Supplementary Note 5.

Fig. 4: More examples.
figure 4

a Applying swapping method to non-Hermitian (NH) Creutz ladder model with magnetic flux represented by imaginary hoppings ± is/2. Gain and loss are denoted by onsite energies ± iγ/2. The system with swapped gain/loss in every second unit cell is displayed on the right side. b, c Applying swapping method to another two variants of NH SSH model. d, e Two dimensional (2D) examples that can be treated by the swapping method: (d) 2D NH SSH model and (e) NH Benalcazar-Bernevig-Hughes model. The swapping procedures are omitted in d and e.

Full size image

Conclusion

We introduced a simple and intuitive approach known as doubling and swapping to restore the BBC in systems exhibiting NHSE, at the expense of involving more bands. The basic principle is to counterbalance the NHSE by swapping the asymmetric hoppings (or gain/loss) in every second primitive unit cell, while keeping the OBC spectrum unchanged. This approach gives the same result as the non-Bloch approach that uses the concept of GBZ. The idea can be applied to a wide range of systems covered in the literature, including those in higher dimensions. Furthermore, we extended the study to disordered systems where asymmetric hoppings are randomly exchanged, causing NHSE strength to fluctuate. For each configuration, the NHSE strength is reflected in the area enclosed by the ring’s spectrum. Similar to the ordered case, two types of winding numbers can be defined to account for the NHSE and topological edge states, respectively.

Methods

Similarity between H obc and \({H}_{obc}^{{\prime} }\)

Below we show that for a general N × N tridiagonal matrix M that represents a chain with nearest-neighbor hoppings, the spectrum remains invariant when any pair of hoppings between two sites are swapped, i.e., Mi,i+1 ↔ Mi+1,i.

For illustration, we consider the following 3 × 3 tridiagonal matrix,

$$M=\left(\begin{array}{ccc}{\epsilon }_{a}&{M}_{12}&0\\ {M}_{21}&{\epsilon }_{b}&{M}_{23}\\ 0&{M}_{32}&{\epsilon }_{c}\end{array}\right).$$
(8)

Its characteristic polynomial has the following form

$$f(\lambda ) = \, \det (\lambda {\mathbb{I}}-M) \\ = \, {\lambda }^{3}-{\lambda }^{2}\left({\epsilon }_{a}+{\epsilon }_{b}+{\epsilon }_{c}\right) \\ -\lambda \left({M}_{12}{M}_{21}+{M}_{23}{M}_{32}-{\epsilon }_{a}{\epsilon }_{b}-{\epsilon }_{a}{\epsilon }_{c}-{\epsilon }_{b}{\epsilon }_{c}\right) \\ -{\epsilon }_{a}{\epsilon }_{b}{\epsilon }_{c}+{M}_{23}{M}_{32}{\epsilon }_{a}+{M}_{12}{M}_{21}{\epsilon }_{c}$$
(9)

Just like Eq. (9), the characteristic polynomial of a general tridiagonal matrix consist of many terms in the form of Mi+1,iMi,i+1, i.e., Mi+1,i and Mi,i+1 always appear together. Swapping the values of Mi+1,i and Mi,i+1 in a general tridiagonal matrix M does not change f(λ) and therefore the eigenvalues of M.

Immediately we can conclude that Hobc and \({H}_{obc}^{{\prime} }\) share the same spectrum, and they are generally equivalent under a similarity transformation except in the rare scenario where EPs are involved and Hobc and \({H}_{obc}^{{\prime} }\) correspond to distinct Jordan normal forms. For example, as we increase t, we encounter such a rare scenario at t = γ/2 when the intracell coupling becomes unidirectional, i.e., t2 = 0. In this case, Hobc and \({H}_{obc}^{{\prime} }\) have distinct Jordan normal forms due to occurrence of EPs, and cannot be related by a similarity transformation.

In a similar vein, we can show that \({H}_{obc}^{{\prime} }\) and a random chain \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) have identical spectrum and are similar in general cases.

Characterization by quantized Berry phase

The topological edges states of Hobc can also be captured by quantized Berry phase, noting that there is inversion symmetry in \({H}^{{\prime} }(k)\).

Since \({H}^{{\prime} }(k)\) is a four-band system, we need to consider the two-band Berry phase. The overlap matrix has the form

$${M}_{mn}^{{k}_{i},{k}_{i+1}}=\left\langle {u}_{m,{k}_{i}}^{L}| {u}_{n,{k}_{i+1}}^{R}\right\rangle ,$$
(10)

where m, n = 1, 2, L and R indicate the left and right eigenvectors, respectively. The two-band Berry phase is then obtained by57

$${\phi }_{B}=-{{{{{{\mathrm{Im}}}}}}}\,\ln \det {\prod }_{i=0}^{N-1}{M}^{{k}_{i},{k}_{i+1}},$$
(11)

A dense enough mesh in calculating Eq. (11) gives us the quantized Berry phase, without the need to involve the singular value decomposition. In our numerical computation, we can skip the k = π point where the band degeneracy occurs. We can also include the k = π point, but it is important to remember the constraint 〈um,k=π∣un,k=π〉 = δmn in order to address the degeneracy-induced ambiguity in the eigenvectors.

Derivation of non-Bloch Hamiltonian H nB(k)

In the text we claimed that \({h}^{{\prime} }(k)\) in Eq. (4) is just the non-Bloch Hamiltonian HnB(k). Below we provide the derivation of HnB(k). The Bloch Hamiltonian for the system in Fig. 1a is

$$h(k)=\left(\begin{array}{cc}0&{t}_{1}+s{e}^{-ik{a}_{0}}\\ {t}_{2}+s{e}^{ik{a}_{0}}&0\end{array}\right).$$
(12)

With the substitution \({e}^{ik{a}_{0}}\to \beta\) in h(k), Eq. (12) becomes

$$h(\beta )=\left(\begin{array}{cc}0&{t}_{1}+s{\beta }^{-1}\\ {t}_{2}+s\beta &0\end{array}\right).$$
(13)

The characteristic polynomial of \(h(\beta )=\det [E-h(\beta )]\) is

$$f(\beta ,E)={E}^{2}-{t}_{1}{t}_{2}-{s}^{2}-{t}_{1}s\beta -{t}_{2}s{\beta }^{-1}.$$
(14)

Following ref. 41, we can solve for the auxiliary generalized Brillouin zone from

$$f(\beta ,E)=f(\beta {e}^{i\Xi },E)=0,$$
(15)

where Ξ is real. Equation (15) contains four real equations if we write the real and imaginary parts separately, and five real variables: \({{{{{{\mathrm{Re}}}}}}}\,(E)\), \({{{{{{\mathrm{Im}}}}}}}\,(E)\), Ξ, \({{{{{{\mathrm{Re}}}}}}}\,(\beta )\) and \({{{{{{\mathrm{Im}}}}}}}\,(\beta )\). By eliminating E in Eq. (15), we get two equations for the three variables Ξ, \({{{{{{\mathrm{Re}}}}}}}\,{{{{{{\mathrm{Re}}}}}}}\,(\beta )\) and \({{{{{{\mathrm{Im}}}}}}}\,(\beta )\):

$${{{{{{\mathrm{Re}}}}}}}\,[G(\beta ,\Xi )]=0,\quad \,{{\mbox{and}}}\,\quad {{{{{{\mathrm{Im}}}}}}}\,[G(\beta ,\Xi )]=0,$$
(16)

where \(G(\beta ,\Xi )={{{{{{{{\mathcal{R}}}}}}}}}_{E}[f(\beta ,E),f(\beta {e}^{i\Xi },E)]\) denotes the resultant58 of f(β, E) and f (βeiΞ, E) with respect to E.

By the Weierstrass substitution \(\cos \Xi =(1-{\tau }^{2})/(1+{\tau }^{2})\) and \(\sin \Xi =2\tau /(1+{\tau }^{2})\), Eq. (16) becomes two algebraic equations of τ, \({{{{{{\mathrm{Re}}}}}}}\,(\beta )\) and \({{{{{{\mathrm{Im}}}}}}}\,(\beta )\), which we rewrite as

$${G}_{r}({\beta }_{r},{\beta }_{i},\tau )=0,\quad \,{{\mbox{and}}}\,\quad {G}_{i}({\beta }_{r},{\beta }_{i},\tau )=0$$
(17)

where we use \({\beta }_{r}\equiv {{{{{{\mathrm{Re}}}}}}}\,(\beta )\), \({\beta }_{i}\equiv {{{{{{\mathrm{Im}}}}}}}\,(\beta )\), \({G}_{r}({\beta }_{r},{\beta }_{i},\tau )\equiv {{{{{{\mathrm{Re}}}}}}}\,[G(\beta ,\tau )]\) and \({G}_{i}({\beta }_{r},{\beta }_{i},\tau )\equiv {{{{{{\mathrm{Im}}}}}}}\,[G(\beta ,\tau )]\).

Using \({{{{{{{{\mathcal{R}}}}}}}}}_{\tau }[{G}_{r}({\beta }_{r},{\beta }_{i},\tau ),{G}_{i}({\beta }_{r},{\beta }_{i},\tau )]=0\), we eliminate τ in Eq. (17) and obtain the equation for the auxiliary GBZ,

$${\left[{t}_{1}({\beta }_{r}^{2}+{\beta }_{i}^{2})-{t}_{2}\right]}^{4}\times {\left[{t}_{1}({\beta }_{r}^{2}+{\beta }_{i}^{2})+{t}_{2}\right]}^{4}=0,$$
(18)

which involves t1 and t2. From Eq. (18), we obtain the arcs of the auxiliary GBZ,

$${t}_{1}({\beta }_{r}^{2}+{\beta }_{i}^{2})=\pm {t}_{2}.$$
(19)

From Eq. (19), we then get the GBZ modulus

$$| \beta | =\sqrt{\left\vert {t}_{2}/{t}_{1}\right\vert }.$$
(20)

With the GBZ parameterized as \(\beta =| \beta | {e}^{ik{a}_{0}}\) substituted into Eq. (13), we get the non-Bloch Hamiltonian

$${\tilde{H}}_{nB}(k)=\left(\begin{array}{cc}0&{t}_{1}+s| \beta {| }^{-1}{e}^{-ik{a}_{0}}\\ {t}_{2}+s| \beta | {e}^{ik{a}_{0}}&0\end{array}\right).$$
(21)

By a similarity transformation \({H}_{nB}(k)={X}^{-1}{\tilde{H}}_{nB}(k)X\) with X = diag(∣β∣−1/2, ∣β∣1/2), we obtain a different form of non-Bloch Hamiltonian

$${H}_{nB}(k)=\left(\begin{array}{ll}0&{t}_{1}| \beta | +s{e}^{-ik{a}_{0}}\\ {t}_{2}| \beta {| }^{-1}+s{e}^{ik{a}_{0}}&0\end{array}\right).$$
(22)

Compared to Eq. (12), the asymmetric intracell hoppings t1,t2 are scaled to t1∣β∣, t2∣β∣−1 in HnB(k) such that t1∣β∣ = ± t2∣β∣−1 and the system HnB(k) is NHSE-free. Obviously the OBC counterpart of HnB(k) shares the same spectrum with that of h(k), H(k), \({H}^{{\prime} }(k)\) or \({h}^{{\prime} }(k)\), noting t1∣β∣ × t2∣β∣−1 = t1t2.

In comparison with HnB(k) in Eq. (22), \({h}^{{\prime} }(k)\) in Eq. (4) of the text comes from a different scaling of the asymmetric intracell hoppings t1,t2 to \(\sqrt{{t}_{1}{t}_{2}}\) such that the system \({h}^{{\prime} }(k)\) is NHSE-free. They are identical when t1 > t2 > 0.

Same \({w}^{{\prime} }\) value for different random SSH chain configurations

Below we show that different random configurations of \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) not only share the common spectrum, but also lead to the same value of winding number \({w}^{{\prime} }\).

We rewrite the real-space formula for the winding number associated with chiral symmetry,

$${w}^{{\prime} }=\frac{1}{{L}^{{\prime} }}{{{{{{{{\rm{Tr}}}}}}}}}^{{\prime} }(SQ[Q,X]),$$
(23)

where \(T{r}^{{\prime} }\) denotes the trace over the middle interval x ∈ [ℓ + 1, L − ℓ] of the chain, and

$$S=diag[1,-1,1,-1,1,-1,\cdots \,],\quad X=diag\{1,1,2,2,\ldots \,\},$$
(24)

and Q represent the chiral symmetry operator, the coordinate operator, and the flattened Hamiltonian. Q is given by

$$Q={\mathbb{I}}-2P$$
(25)

with \(P={\sum}_{i = 1}^{\ell /2} | {\phi }_{i}^{R}\rangle \langle {\phi }_{i}^{L}|\) being the projection operator of the eigenstates with lower energy E (or \({{{{{{\mathrm{Re}}}}}}}\,E\)).

Without loss of generality, for any two different random chain configurations, e.g., \({{{{{{{{\mathcal{H}}}}}}}}}_{c}\) and \(\bar{{{{{{{{{\mathcal{H}}}}}}}}}_{c}}\), we assume that they are related by a similarity transformation,

$$\bar{{{{{{{{{\mathcal{H}}}}}}}}}_{c}}=U{{{{{{{{\mathcal{H}}}}}}}}}_{c}{U}^{-1}.$$
(26)

Correspondingly, their projection operators and flatten Hamiltonians are related by

$$\bar{P}=UP{U}^{-1},\quad \bar{Q}=UQ{U}^{-1}.$$
(27)

It is important to note that S, X and U are all diagonal matrices, and \({\bar{Q}}^{2}={({\mathbb{I}}-2\bar{P})}^{2}=4{\bar{P}}^{2}-4\bar{P}+{\mathbb{I}}={\mathbb{I}}\) using \({\bar{P}}^{2}=\bar{P}\).

We have

$${(\bar{Q}X\bar{Q})}_{ii} = \,{(UQ{U}^{-1}XUQ{U}^{-1})}_{ii}={\sum}_{j}{U}_{ii}{Q}_{ij}{U}_{jj}^{-1}{X}_{jj}{U}_{jj}{Q}_{ji}{U}_{ii}^{-1}\\ = {\sum}_{j}{U}_{ii}{Q}_{ij}{X}_{jj}{Q}_{ji}{U}_{ii}^{-1}={\sum}_{j}{Q}_{ij}{X}_{jj}{Q}_{ji}={(QXQ)}_{ii},$$
(28)

where \({U}_{jj}^{-1}\equiv {({U}^{-1})}_{jj}\). Then we have

$${{{\mbox{Tr}}}}^{{\prime} }(S\bar{Q}X\bar{Q}) = {\sum }_{i={\ell }_{0}+1}^{L-{\ell }_{0}}{\sum}_{j}{S}_{ii}{\bar{Q}}_{ij}{X}_{jj}{\bar{Q}}_{ji}={\sum }_{i={\ell }_{0}+1}^{L-{\ell }_{0}}{S}_{ii}{\sum}_{j}{\bar{Q}}_{ij}{X}_{jj}{\bar{Q}}_{ji}\\ = {\sum }_{i={\ell }_{0}+1}^{L-{\ell }_{0}}{S}_{ii}{(\bar{Q}X\bar{Q})}_{ii}={\sum }_{i={\ell }_{0}+1}^{L-{\ell }_{0}}{S}_{ii}{(QXQ)}_{ii}={{{\mbox{Tr}}}}^{{\prime} }(SQXQ),$$
(29)

where the fourth equality used Eq. (28).

Finally we find the relation

$$\bar{{w}^{{\prime} }} = \, \frac{1}{{L}^{{\prime} }}{{{\mbox{Tr}}}}^{{\prime} }(S\bar{Q}[\bar{Q},X])= \, \frac{1}{{L}^{{\prime} }}{{{\mbox{Tr}}}}^{{\prime} }(S{\bar{Q}}^{2}X-S\bar{Q}X\bar{Q})= \, \frac{1}{{L}^{{\prime} }}{{{\mbox{Tr}}}}^{{\prime} }(SX-S\bar{Q}X\bar{Q})\\ = \frac{1}{{L}^{{\prime} }}[{{{\mbox{Tr}}}}^{{\prime} }(SX)-{{{\mbox{Tr}}}}^{{\prime} }(S\bar{Q}X\bar{Q})]= \, \frac{1}{{L}^{{\prime} }}[{{{\mbox{Tr}}}}^{{\prime} }(SX)-{{{\mbox{Tr}}}}^{{\prime} }(SQXQ)] \\ = \, \frac{1}{{L}^{{\prime} }}{{{\mbox{Tr}}}}^{{\prime} }(SQ[Q,X]) ={w}^{{\prime} },$$
(30)

where \({\bar{Q}}^{2}={\mathbb{I}}\) is used in the third equality, and Eq. (29) is used in the fifth equality. Equation (30) shows that the winding number is exactly equal for any two different random chain configurations, i.e., the random swapping itself does not change the value of the winding number as long as the same L, ℓ are taken.

Similarity between SSH model and Creutz ladder model in the presence of disorder

The Bloch Hamiltonians of the SSH model and Creutz ladder model, which we denote as h(k) and \({{{{{{{{\mathcal{H}}}}}}}}}_{l}(k)\), are related by the following similarity transformation:

$${R}^{-1}h(k)R={{{{{{{{\mathcal{H}}}}}}}}}_{l}(k),$$
(31)

where

$$h(k) = \, (t+s\cos k){\sigma }_{x}+(s\sin k+i\gamma /2){\sigma }_{y} \\ = \, \left(\begin{array}{rc}0&{t}_{1}+s{e}^{-ik} \\ {t}_{2}+s{e}^{ik}&0\end{array}\right), \\ {{{{{{{{\mathcal{H}}}}}}}}}_{l}(k) = \, (t+s\cos k){\sigma }_{x}+(s\sin k+i\gamma /2){\sigma }_{z} \\ = \, \left(\begin{array}{rc}s\sin k+i\gamma /2&t+s\cos k\\ t+s\cos k&-s\sin k-i\gamma /2\end{array}\right),$$
(32)

and

$$R={e}^{i{\sigma }_{x}\pi /4}=\frac{1}{\sqrt{2}}\left(\begin{array}{rc}1&i\\ i&1\end{array}\right).$$
(33)

In the presence of random swapping, the Hamiltonians of the SSH chains (rings) and Creutz ladder chains (rings) are related by the following similarity transformation,

$${X}^{-1}{h}^{{\prime} }X={{{{{{{{\mathcal{H}}}}}}}}}_{l}^{{\prime} },$$
(34)

where

$$X=R\oplus R\oplus \cdots \oplus R$$
(35)

is a block diagonal matrix, as long as the indices of swapped unit cells in the two systems coincide. It is obvious that Eq. (34) also applies to the finite unswapped and the orderly swapped chains (rings).

For any given t, s, γ values, all the random SSH chains and random Creutz ladder chains share the same spectrum, and a similarity transformation generally exists between any two of them.