Introduction

Schrödinger’s gedanken experiment involving a cat in a superposition of dead and alive states vividly demonstrates the magical picture of quantum superposition on a macro scale1. In modern physics, this cat state (CS) is usually represented by the superposition of two distinct coherent states |±α〉, which can generally be considered orthogonal when |α| ≥ 2. With the increase of amplitude |α|, CS gets closer to the macroscopic superposition, making it an important resource for the study of macroscopic quantum phenomena. CS is not only attractive from a fundamental point of view2,3, but also valuable for applications including quantum teleportation4,5,6, quantum computing7,8,9,10,11, quantum error correction12,13,14,15,16,17 and quantum metrology18,19,20,21,22,23,24. After decades of efforts, CS is now being generated on various platforms3,25,26,27,28. However, even for the best experimental results in the optical domain so far |α| remains less than 229,30,31,32,33,34,35,36,37, and it remains a challenge to increase the value of |α| based on existing methods. For example, the widely studied photon subtraction method29,30,31,32,33,38,39, which is a probabilistic method based on post-selection, has low probability of success for generating large-amplitude CS. Another approach that has attracted a lot of attention is the synthesis method36,40,41, which uses a pre-prepared CS as a seed to grow large-amplitude CS. However, this method is still limited by the amplitude of the pre-prepared CS. Furthermore, a deterministic method that based on light-matter interaction42 has recently been demonstrated experimentally37. In this method, CS is generated by direct interaction between an incident coherent light pulse and a single-side cavity containing a three-level atom37,42,43,44,45. Its basic idea is to use normal-mode splitting43 to control the phase of the reflected coherent light field. In the experiment, the amplitude of the output CS is |α| ≈ 1.437. Unfortunately, this method is limited in preparing an arbitrarily large |α| CS for a given optical pulse length, due to the fragility of the atom-cavity coupling system when interacting with a strong light field. As the external field strengthens, a single atom ultimately cannot prevent the optical field from entering the cavity, resulting in the reflected field carrying a π phase shift regardless of the atomic state, similar to what occurs with empty cavity reflection.

Needless to say, optical field is an excellent medium for information transmission. Considering the practical application requirements that involve integrating diverse quantum systems, as well as for advanced sensing and imaging techniques, the generation of optical CS with large amplitudes and customizable propagation properties becomes not only necessary but also of significant value. This endeavor represents a pioneering frontier in the realm of quantum optics, bearing profound implications for both the theoretical understanding and the advancement of practical quantum technology46.

In this article, we propose a deterministic method to generate flying optical CS whose amplitude can be arbitrarily large, provided that optical losses from classical optical devices remain low. The key step of our scheme is to entangle a strong coherent light field with a microscopic quantum system prepared in a superposition state initially. After the entanglement, the optical CS is obtained by performing projection measurement on the quantum microsystem. In response to the situation that a quantum microsystem is typically very fragile when facing strong light fields, our solution is to utilize interaction-free measurement based on quantum Zeno effect47,48,49, which is considered a powerful non-invasive measurement method that can protect vulnerable samples. In this work, we further apply it to protect the quantum properties of the microscopic system from destruction by strong fields. We replace the direct interaction between the strong light field and the microsystem with a sequence of interactions, each with only a small fraction of photons actually interacting with the microsystem. This ensures that the quantum microsystem always works in a weak field environment, making one of the main advantages of this work. Eliminating the negative influence of strong fields gives liberty of applying this method in a wide variety of systems and provides the potential for future applications. More importantly, this indicates that our scheme allows quantum microscopic systems to manipulate macroscopic counterparts that are challenging to control directly. In addition, our method has another important advantage—it can reduce the requirements of quantum microscopic systems. For illustration, we employ the single-side cavity-atom coupling model37 as our specific quantum microscopic system. Our simulation shows that our scheme becomes less and less sensitive to both atomic spontaneous emission and detuning between the atom and the cavity as the number of interactions increases, when other classical optical devices are ideal. This enables our method to reduce the impact of optical losses originating from quantum device (referred to as Type I light loss), with the main limitation of our method arising from the optical losses introduced by classical optical devices (referred to as Type II light loss). Finally, it is also worth mentioning that here we mainly focus on the optical platform, but our approach can also be extended to other platforms such as superconducting microwave resonator50,51.

Results and discussion

General multiple reflection scheme

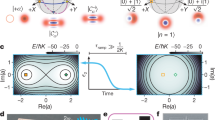
First, we focus on explaining the principle of our method. More detailed experimental protocols will be discussed later. We start with the chain Mach-Zehnder interferometer shown in Fig. 1a, which is a commonly used optical structure for interaction-free measurement52,53,54,55,56,57. Compared to conventional interaction-free measurement studies, our scheme has two distinct features, although these are commonly used and even necessary for CS preparation. Firstly, we use a coherent light source (S) instead of a single photon source. Secondly, conventional interaction-free measurement typically assume that an object has two functions: absorbing photons or allowing them to pass through. However, our method introduces an additional function for the object, which is to apply a π phase shift to the light field passing through it. In details, as shown in Fig. 1a, MR stands for normal mirror, and BS stands for beam-splitter. The interference occurs between the light fields in Zones 0 and 1, which are located on the lower and upper sides of BS, respectively, separated by a dotted line. Assuming that \({a}_{z}^{{{\dagger}} }\) (z = 0, 1) represents the creation operator of the light field in Zone z, the function of BS can be described by \({a}_{0}^{{{\dagger}} }\to {a}_{0}^{{{\dagger}} }\cos \theta +{a}_{1}^{{{\dagger}} }\sin \theta\) and \({a}_{1}^{{{\dagger}} }\to {a}_{1}^{{{\dagger}} }\cos \theta -{a}_{0}^{{{\dagger}} }\sin \theta\)49\(,\) where cos2 θ represents the reflectivity of BS. As for the object, it has three states, |pass〉, |block〉, and |phase〉. Firstly, we discuss the state |pass〉, where the object is transparent, thereby causing optical interference to occur continuously in Zones 0 and 1. Assuming the initial state of the light field is such that the field in Zone 0 is in the coherent state |α〉 and the field in Zone 1 is in the vacuum state |0〉, it is represented as \(\left|\alpha,0\right\rangle =\exp \left(\alpha {a}_{0}^{{{\dagger}} }-{\alpha }^{* }{a}_{0}\right){{|}}0,0{{\rangle }}\). After passing through N number of BSs, it becomes |α cos Nθ, α sin Nθ 〉58. Apparently, when θ = π/2N, we have |0, α〉. While when θ = π/N, we have |−α, 0〉. Secondly, we discuss the state |block〉. In this case, any photon passing through the object is absorbed. Notice that the object and the light field interact many times. To take into account all absorbed photons, we write the state of the light field as |C0, C1〉|l1, l2,…lN−1〉, where |Cz=0,1〉 represents photon state in Zone z and |l1, l2,…lN−1〉 represents the photon absorbed each time. After the light pulse passing through the first BS, the initial state |α, 0〉|0, 0,…0〉 evolves to |αcosθ, αsinθ 〉|0, 0,…0〉, and it further becomes |αcosθ, 0〉|αsinθ, 0,…0〉 due to the absorption of the object. Subsequently, the photons remaining inside the interferometers pass through the next BS and interact with the object again. Such process repeats N times. After N numbers of BSs, the photon state is \(\left|\alpha {\cos }^{N}\theta ,\alpha {\cos }^{N-1}\theta \sin \theta \right\rangle {\prod }_{n=1}^{N-1}{{|}}\alpha {\cos }^{n-1}\theta \sin \theta {{\rangle }}\). Note that when θ = π/N, as N → ∞, we have cosN θ → 1 and sin θ → 0. Therefore, as long as |α|2 is finite, the light field can be frozen in its initial state |α, 0〉|0, 0,…0〉. This also means that the actual number of photons absorbed by the object during the entire process is close to zero. The object is spared from being directly exposed to light field due to the interruption of the interference process, which can be considered the quantum Zeno effect caused by photon loss. Besides the state |block〉, the state |phase〉 can also maintain the light field in its initial state by applying a π phase shift (\({a}_{1}^{{{\dagger}} }\to -{a}_{1}^{{{\dagger}} }\)) to the photons passing through it. When the photons encounter an odd number of BS, the state becomes |αcosθ, αsinθ〉, while after passing through an even number of BS, it becomes |α, 0〉. It’s important to note that the maximum intensity of photons actually passing through the object during each interaction is |αsinθ|2. When θ = π/N, this value tends to zero as N increases, suggesting the freezing of the light field. Consequently, for both states |block〉 and |phase〉, the object works in a weak field environment.

Fig. 1: Schematic for cat state preparation.
figure 1

S represents the coherent light source, BS the beam-splitter, MR the normal mirror, SM the switchable mirror, PS the phase shifter, and C the optical circulator. a Principle model based on a chain interferometer. b Multiple reflection scheme based on a Michelson interferometer. When the switchable mirrors (SM) are turned on, the coherent light pulse bounces inside the interferometer and interacts with the single-side cavity (SSC) M times. The SSC consists of two mirrors, CMT and CMR, with CMT assumed to have perfect reflectivity under ideal conditions. Only SSC1 contains a three-level atom. c The energy level structure of the atom, where the cavity mode couples only with the transition between levels |↑〉 and |e〉. The atom is prepared in superposition state \((|\downarrow \rangle + |\uparrow \rangle ) / \sqrt{2}\)).

Full size image

Above, we have introduced the three states of the object and the corresponding dynamic evolution behavior of the light field. It is easy to see that if an object is initially in a superposition state of \(\left(\left|{{{{{\rm{pass}}}}}}\right\rangle +\left|{{{{{\rm{block}}}}}}\right\rangle \right)/\sqrt{2}\) or \(\left(\left|{{{{{\rm{pass}}}}}}\right\rangle +\left|{{{{{\rm{phase}}}}}}\right\rangle \right)/\sqrt{2}\), the object can be entangled with the coherent light field when θ = π/N, i.e., \(\left(|-\alpha ,0\rangle \left|{{{{{\rm{pass}}}}}}\right\rangle +|\alpha ,0\rangle \left|{{{{{\rm{block}}}}}}/{{{{{\rm{phase}}}}}}\right\rangle \right)/\sqrt{2}\). After measuring the object with \(\left(\left|{{{{{\rm{pass}}}}}}\right\rangle \pm \left|{{{{{\rm{block}}}}}}/{{{{{\rm{phase}}}}}}\right\rangle \right)/\sqrt{2}\), CS can be deterministically created. However, whether it turns out to be an odd or even CS is random, each with a 50% probability of occurrence. The even CS occurs when the measurement result is \(\left(\left|{{{{{\rm{pass}}}}}}\right\rangle +\left|{{{{{\rm{block}}}}}}/{{{{{\rm{phase}}}}}}\right\rangle \right)/\sqrt{2}\). As for the other measurement result, the odd CS is obtained. In addition, it is worth mentioning that our method can also realize the entangled coherent state \(\left(\left|\alpha ,0\right\rangle +\left|0,\alpha \right\rangle \right)/\sqrt{2}\)20,21\(.\) To do so, we just need to set θ = π/2N. Given that the optical field is reflected and interacts with the quantum object many times, we refer to the above method as the multiple reflection scheme in the following discussion.

Multiple reflection scheme using single-side cavity-atom coupling system

The above is the basic idea of our method. The next important issue is what kind of real quantum microscopic system can be used as an object for our scheme. We have shown that it is optional whether the object absorbs photons or provides a π phase. The difference is that the latter way does not introduce any photon loss. In theory, it has better fidelity. Nevertheless, given that photon loss due to device imperfection is inevitable in real systems, the former mechanism is also critical. In fact, our later numerical calculations will show that such mechanism can even mitigate the impact of optical losses caused by the quantum system, indicating that the optical loss of the quantum microsystem no longer serves as the decisive factor when choosing a microsystem for our multiple reflection scheme. Microsystems capable of implementing optical path blocking, such as Rydberg blockade59,60,61, photon blockade62, and so on58,63, remain viable candidates for applying our method. Regardless of the system type, our scheme allows the microsystem to function properly within a weak field environment. This represents the primary contribution of our work, enabling our scheme to be utilized in any given experimental environment and offering potential for future practical application. In the following, we will analyze a detailed experimental scheme based on a specific microscopic system in order to study the performance of our method under realistic conditions.

For illustrative purposes only, we adopt the atom-single side cavity system37 as our quantum microsystem. As shown in Fig. 1b, a single atom is embedded in a single-side cavity SSC1, which is constituted by two facing mirrors CMR and CMT. Ideally, CMT is assumed to have perfect reflection, but CMR is allowed for in- and outcoupling of light. The energy level configuration of the atom is shown in Fig. 1c. The transition between levels |↑〉 and |e〉 is coupled by the cavity mode. When the atom is in |↑〉, the weak coherent light pulse, resonant with the cavity, is prevented from entering the cavity due to normal-mode splitting, which results in reflection without a π phase shift. As for the transition between |↓〉 and |↑〉, it is decoupled from the cavity mode due to large detuning. Therefore, when the atom is in |↓〉, the cavity can be treated as an empty cavity. The incident pulse enters the cavity and reflects back but with a π phase. This atom-cavity coupling model has been directly used to generate CS37,42. After a single reflection (Hereinafter we call it the single reflection scheme), the atom-field entanglement \((\left|\alpha \right\rangle \left|\uparrow \right\rangle +\left|-\alpha \right\rangle \left|\downarrow \right\rangle )/\sqrt{2}\) can be generated. Unfortunately, we will later explain why the method becomes ineffective when the incident light field is strong, but our solution can address this problem.

Based on the atom-cavity system, our detailed experimental scheme is presented in Fig. 1b. In order to implement multiple interactions between the atom and light field, we do not directly use the chain interferometer structure in Fig. 1a, but rather its equivalent Michelson interferometer. In the figure, SM stands for switchable mirror (In the experiment, it can be realized by a fiber switch64 or Pockels cell65,66,67,68), which is transparent only at the beginning and end of preparation. At all other times, it is just a normal mirror, forcing the light pulse to bounce back and forth inside the interferometer for M cycles. One cycle is defined by a pulse starting at SM, going through BS twice, and returning to SM. Because the optical field passes through the BS twice during each interaction with the atom, we adjust the parameter of BS to θ = π/2M. In addition, SSC0 is an empty single-side cavity. Except for the absence of atom, everything else is the same as SSC1. C stands for optical circulator. PS stands for phase shifter. Unlike other components, the use of PS is only for the convenience of calculation and discussion. Its removal does not have a substantial impact on our method. We assume that PS adds a π phase shift to the light field only as it propagates from BS to SSC. Its function can be described as \({a}_{z}^{{{\dagger}} }\to -{a}_{z}^{{{\dagger}} }\), where we still set \({a}_{z}^{{{\dagger}} }\) (z = 0, 1) as the creation operator of the light field in Zone z.

Initially, the light source emits a coherent pulse into the interferometer, while the light field in Zone 1 is in a vacuum state. As for the atom, it is prepared in a superposition state. Accordingly, the initial state of the entire system is \(\left|\alpha ,0\right\rangle \left(\left|\uparrow \right\rangle +\left|\downarrow \right\rangle \right)/\sqrt{2}\). After m number of cycles, the wave-function of the whole system becomes (See the “System wave-function calculation” subsection in the Methods)

$$\left|{\psi }^{\left(2m\right)}\right\rangle =\frac{1}{\sqrt{2}}\left(\left|\alpha ,0\right\rangle \left|\uparrow \right\rangle +\left|\alpha \cos 2m{\theta }_{M},\alpha \sin 2m{\theta }_{M}\right\rangle \left|\downarrow \right\rangle \right)$$
(1)

The dynamic evolution process of the system can be briefly described as follows. Due to the presence of the empty cavity SSC0, when the atom is in |↓〉, light field has no phase difference in Zones 0 and 1. Interference continues to occur, thereby generating |−α〉. On the contrary, when the atom is in |↑〉, the light field is frozen in |α〉 due to the phase difference between the two Zones. Consequently, after M cycles, we have the light-atom entangled state \(\left(\left|\alpha ,0\right\rangle \left|\uparrow \right\rangle +\left|-\alpha ,0\right\rangle \left|\downarrow \right\rangle \right)/\sqrt{2}\). We note that the light field is output from the SM0 end and no photons appear at SM1 side. After measuring the atom, the optical CS is deterministically prepared.

So far, we have only focused on the ideal case. In the following, we analyze the performance of our multiple reflection scheme for non-ideal situation. We show that our scheme is highly durable when it comes to parameters such as atomic spontaneous emission decay and atom-cavity detuning. The reason for this is the quantum Zeno effect caused by light absorption.

Experimental parameter analysis of multiple reflection scheme based on single-side cavity-atom coupling system

In the upcoming discussion, we utilize numerical simulations to analyze the impact of various practical parameters, including atomic, cavity parameters, the number of cycles, and the light loss rates of classical optical devices. We employ fidelity and cattiness69,70,71 as metrics to assess the quality of the CS generated by our method. Additionally, recognizing the critical role of light loss in CS preparation71, the two types of optical losses categorized in the introduction are the focus of our discussion. The first type is caused by the quantum system, specifically the atom-cavity interaction, while the second type solely originates from classical optical devices.

To begin with, we briefly outline the definitions of each parameter. Regarding the practical atom-cavity system (SSC1), the incident light field is not only reflected, but also transmitted and scattered. To evaluate these effects, we set that 2γ and ωa as the spontaneous emission decay rate and transition frequency of the atomic transition between |e〉 and |↑〉, respectively. The coupling constant between the cavity mode of frequency ωc and the atomic transition is g. The atom-cavity detuning is Δ = ωa − ωc. Moreover, we set κR(T) as the cavity field decay rate into the external light field on the CMR(T) side. Given that the atom is hardly excited in our scheme, as long as the condition of slowly varying light intensities is satisfied37,45,72, SSC1 can be well described by the input-output theory73,74. Suppose that |αi,1↑〉 is the incident coherent light field from CMR1 side when the atom is in |↑〉. The cavity reflection |αR,1↑〉 satisfies (See the “Input-output theory for the atom-cavity coupling system” subsection in the Methods)

$${\alpha }_{{{{{{\rm{R}}}}}},1\uparrow }=\left[1-\frac{2{\kappa }_{{{{{{\rm{R}}}}}}}\left({{{{{\rm{i}}}}}}\Delta +\gamma \right)}{\kappa \left({{{{{\rm{i}}}}}}\Delta +\gamma \right)+{g}^{2}}\right]{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }={{|}}{\eta }_{{{{{{\rm{R}}}}}},1\uparrow }{{|}}{e}^{{{{{{\rm{i}}}}}}{\beta }_{{{{{{\rm{R}}}}}},1\uparrow }}{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }$$
(2)

where κ = κR + κT, |ηR,1↑|2 is the reflectivity and βR,1↑ describes the phase of the reflection. Similarly, for the transmission of the cavity |αT,1↑〉, we have

$${\alpha }_{{{{{{\rm{T}}}}}},1\uparrow }=-\frac{2\left({{{{{\rm{i}}}}}}\Delta +\gamma \right)\sqrt{{\kappa }_{{{{{{\rm{T}}}}}}}{\kappa }_{{{{{{\rm{R}}}}}}}}}{\kappa \left({{{{{\rm{i}}}}}}\Delta +\gamma \right)+{g}^{2}}{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }$$
(3)

Regarding the scattering field |αS,1↑〉 due to the atomic spontaneous emission, we have

$${\alpha }_{{{{{{\rm{S}}}}}},1\uparrow }=\frac{2g\sqrt{{\kappa }_{{{{{{\rm{R}}}}}}}\gamma }}{\kappa \left({{{{{\rm{i}}}}}}\Delta +\gamma \right)+{g}^{2}}{\alpha}_{{{{{{\rm{i}}}}}},1\uparrow }$$
(4)

As for the situation that the atom is in |↓〉, we still assume that the atom is completely unaffected by the cavity mode due to the large detuning. Therefore, SSC1 in such case can be treated the same as the empty cavity SSC0. By setting g = 0 in Eqs. (2)–(4), we can immediately obtain the corresponding reflection and transmission. As for the scattering light field, it is 0.

Before we continue our parameter analysis, let us make some necessary discussions about Eqs. (2)–(4). They constitute the mathematical foundation of the single reflection model, and seem unrelated to the intensity of the input light |α|2. It is true that the single reflection model allows for a certain degree of flexibility in |α|2. However, to derive Eqs. (2)–(4), the weak excitation approximation is required (see Eq. (15) in Methods), meaning that the light field inside the cavity cannot be too strong. This leads to the requirement that the cavity parameter κR not be too large, and similarly, the intensity of the incident field or the peak value of the incident pulse must also be constrained. In fact, when parameters such as κR, κT, γ, Δ, g and pulse length are fixed, increasing the intensity of the incident light always invalidates Eqs. (2)–(4). Consequently, to guarantee the single reflection model functions properly, further improvement of the system parameters is necessary. Overcoming these limitations is one of the objectives of our work. Our scheme ensures that the single-side cavity-atom coupling system can always work under the appropriate external field intensity. This effectively leads to avoid the difficulties brought about by improvement of the quantum system. From this perspective, our method is not a negation of the single reflection method. The core principle of our approach is to enhance and broaden the operational range of the atom-cavity coupling system. The two methods are complementing each other.

Based on Eqs. (2)–(4), we can numerically simulate the dynamic evolution of the input coherent pulse, and the fidelity of the output in the multiple reflection scheme. We suppose that the target state is \(|{\psi }_{{{{{{\rm{T}}}}}}}\rangle =(|\alpha \rangle |\!\!\uparrow \rangle +|-\alpha \rangle |\!\!\downarrow \rangle )/\sqrt{2}\), and the final state of the whole system after M cycles is \(|{\psi }_{{{{{{\rm{f}}}}}}}\rangle =(|{C}_{0\uparrow }\rangle |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow }\rangle |\!\!\uparrow \rangle +|{C}_{0\downarrow }\rangle |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\downarrow }\rangle |\!\!\downarrow \rangle )/\sqrt{2}\) with \(|{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow (\downarrow )}\rangle =|{C}_{1\uparrow (\downarrow )}\rangle \otimes {\prod }_{m=1}^{M}|{\alpha }_{{{{{{\rm{T}}}}}},0\uparrow (\downarrow )}^{(m)}\rangle |{\alpha }_{{{{{{\rm{S}}}}}},0\uparrow (\downarrow )}^{(m)}\rangle |{\alpha }_{{{{{{\rm{T}}}}}},1\uparrow (\downarrow )}^{(m)}\rangle |{\alpha }_{{{{{{\rm{S}}}}}},1\uparrow (\downarrow )}^{(m)}\rangle\). Here state |Cz↑(↓)〉 (z = 0, 1) denotes the outputs appearing at SMz side when the atom is in state |↑(↓)〉. \(|{\alpha }_{{{{{{\rm{T}}}}}},z\uparrow (\downarrow )}^{(m)}\rangle\) denotes the transmission field generated by SSCz in the m-th cycle, while \(|{\alpha }_{{{{{{\rm{S}}}}}},z\uparrow (\downarrow )}^{(m)}\rangle\) denotes the scattering field. Given that |loss↑(↓)〉 includes all optical losses caused by the atom-cavity coupling system, the fidelity is calculated by taking the trace of |loss↑(↓)〉, i.e., \(F=T{r}_{{{{{{\rm{loss}}}}}}}\{\langle {\psi }_{{{{{{\rm{T}}}}}}}|{\psi }_{{{{{{\rm{f}}}}}}}\rangle \langle {\psi }_{{{{{{\rm{f}}}}}}}|{\psi }_{{{{{{\rm{T}}}}}}}\rangle \}=\{{\langle \alpha |{C}_{0\uparrow }\rangle |}^{2}+{|\langle -\alpha |{C}_{0\downarrow }\rangle |}^{2}+2{{{{\mathrm{Re}}}}}[\langle \alpha |{C}_{0\uparrow }\rangle \langle {C}_{0\downarrow }|-\alpha \rangle \langle {{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\downarrow }|{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow }\rangle ]\}/4.\) In addition to fidelity F, we also investigate cattiness69,70,71, Ca = (|〈loss↑|loss↓〉|2 − |〈C0↑|C0↓〉|2)|C0↑ − C0↓|2/4. Detailed calculations can be found in the “Cattiness calculation” subsection in the Methods. This physical quantity characterizes the purity of the prepared CS. Its maximum value is equal to |α|2. Apparently, Ca is more sensitive to light loss compared to F, since its value is related to |〈loss↓|loss↑〉|2, while F is solely related to |〈loss↓|loss↑〉|.

As a comparison, we simulate the single reflection model37 as well. More specifically, the input |α〉 is directly reflected by SSC1, and the corresponding output state is \((|{\alpha }_{{{{{{\rm{R}}}}}},1\uparrow }\rangle |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow }\rangle |\!\!\uparrow \rangle +|{\alpha }_{{{{{{\rm{R}}}}}},1\downarrow }\rangle |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\downarrow }\rangle |\!\!\downarrow \rangle )/\sqrt{2}\) with |loss↑(↓)〉 = |αT,1↑(↓)〉|αS,1↑(↓)〉. In this model, the constraints on the atomic parameters γ and Δ can be directly obtained from Eq. (2). For the empty cavity case (atom is in |↓〉), as long as κT = 0, the ideal reflection αR = −αi can be obtained. As for the case where the atom is in |↑〉, the condition for ideal reflection αR = αi is Δ = γ = κT = 0. If only γ is non-zero, we can see that the ideal reflection can be approximately achieved only when γ ≪ g2/κR. As γ increases, the cavity reflectivity |ηR,1↑|2 decreases monotonically until it drops to 0 when γ = g2/κR. In other words, γ causes of the first type of light loss. If we focus on Δ, however, it only affects βR,1↑ when γ = κT = 0, since |ηR,1↑|2 = 1. As Δ varies from −∞ to ∞, βR,1↑ decreases monotonically from π to −π. In order to ensure that βR,1↑ is close to 0, the constraint Δ ≪ g2/κR is required. Our subsequent numerical simulations will demonstrate that satisfying the constraints γ ≪ g2/κR and Δ ≪ g2/κR is necessary for the single reflection model to function properly. In our multiple reflection scheme, however, the above constraints are relaxed.

Effect of atomic spontaneous emission decay rate γ

The atomic parameter γ is the primary source of the first type of light loss. To analyze its effect, we plot the fidelity F and cattiness Ca against \(\widetilde{\gamma }={\kappa }_{{{{{{\rm{R}}}}}}}\gamma /{g}^{2}\) with g = 2π × 7.8 MHz, κR = κ = 2π × 2.3MHz and Δ = 0 in Fig. 2, where \(1/\widetilde{\gamma }\) is the cooperativity. In this simulation, we assume that all classical optical devices such as SM are ideal. The yellow dotted-dashed curve is plotted for the single reflection model with |α|2 = 4, which has almost reached the upper limit of such model37. The remaining curves illustrate the multiple reflection model. Red curves correspond to |α|2 = 4, black to |α|2 = 10, and blue to |α|2 = 16. Dotted curves are used for M = 5, dashed curves for M = 20, solid curves for M = 100, and double-dotted-dashed curves for M = 1000. In addition, vmax is plotted in Fig. 2c for M = 20, where \({v}_{\max }=\max \left\{{\left|{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }^{\left(1\right)}\right|}^{2},{\left|{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }^{\left(2\right)}\right|}^{2},\ldots ,{\left|{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }^{\left(m\right)}\right|}^{2}\ldots \right\}\) is the maximum value of the average photon number reaching SSC1 in each single cycle across all cycles when the atom is in |↑〉. As shown in the figure, vmax is always less than 1 (For other M, the situation is similar), which validates the low atomic excitation probability condition, hence Eqs. (2)–(4) are valid for simulations.

Fig. 2: Influence of atomic spontaneous emission decay.
figure 2

a Fidelity F and (b) cattiness Ca versus dimensionless \(\widetilde{\gamma }={\kappa }_{{{{{{\rm{R}}}}}}}\gamma /{g}^{2}\) with g = 2π × 7.8 MHz, κR = κ = 2π × 2.3 MHz and Δ = 0. The yellow dotted-dashed curve represents the single reflection case. Other curves represent the multiple reflection case with different colors indicating different |α|2 and different styles indicating different M. c We plot vmax versus \(\widetilde{\gamma }\) when M = 20, where vmax is the maximum value of the average photon number reaching SSC1 in each single cycle across all cycles when the atom is in |↑〉.

Full size image

By comparison, we can see that the multiple reflection scheme outperforms the single reflection scheme. In our scheme, it is evident that fidelity increases as M increases. Whereas for larger |α|2, larger M is required to achieve the same fidelity. More importantly, for γ much larger than 2π × 3.0 MHz (This value is taken from the experiment37. It corresponds to \(\widetilde{\gamma }\approx 0.11\) and has been marked in the figure), our scheme can still provide large F. To better explain the result, we consider the extreme case when \(\widetilde{\gamma }=1\), which means all photons reaching SSC1 in a single cycle are lost when the atom is in |↑〉. Under such conditions, the interference between Zone 0 and Zone 1 is continuously interrupted, resulting in the output light field state in Zone 0 becomes |αcos2(π/2M)cosM−1 2(π/2M)〉 ≈ |α(1 − π2/2M)〉48,49, where the approximation is valid when M is sufficiently large. It is evident that when M ≫ |α|, the output photon state approaches |α〉, signifying that the total light loss induced by the atom-cavity coupling system over the entire preparation process (M cycles) is actually significantly suppressed. This phenomenon is a manifestation of the quantum Zeno effect, which is caused by photon loss in the individual atom-cavity coupling system. We note that the cumulative loss is directly proportional to |α|2 and inversely proportional to M, which explains why in Fig. 2a, the larger M and the smaller |α|2, the better the fidelity. So far, our discussion is about \(\widetilde{\gamma }=1\). As for the case of \(0\, < \,\widetilde{\gamma }\, < \,1\), the situation is similar. There is a mixture of two physical mechanisms. The first is to maintain the initial state by phase modulation, which does not cause any photon loss. The second is the quantum Zeno effect, which brings photon loss to the entire system. As \(\widetilde{\gamma }\) increases, the role of the second mechanism becomes increasingly important. Fortunately, by increasing M, the total loss can be greatly suppressed, which indicates that the quantum Zeno effect determines the lower bound of fidelity of our scheme. Together, the above two mechanisms ensure that our scheme has higher fidelity and higher tolerance to γ than the single reflection scheme as M increases. In addition, since the condition γ ≪ g2/κR is relaxed, it implies that our scheme does not require strong coupling between atom and cavity when the value of γ is fixed.

Regarding cattiness, due to its greater sensitivity to light loss, achieving high cattiness requires much smaller light loss than the fidelity case. This necessitates a larger value of M. Consequently, we have plotted the blue double-dotted dashed curve for |α|2 = 16, M = 1000 in Fig. 2b. It is evident that even when the light loss in an individual atom-cavity coupling system is 100%, the cattiness can still exceed 10. In conjunction with our discussion on fidelity, even for significantly large values of |α|2, our scheme can ensure high fidelity and cattiness, provided the condition M ≫ |α| is satisfied. This means that Type I loss does not limit the size of CS that our scheme can produce.

Effect of atom-cavity detuning Δ

Following the analysis of γ, we discuss the impact of Δ. We have shown that by interrupting the interference, the transmission of the light field from Zone 0 to Zone 1 can be suppressed. Note that the phase mismatch between the two Zones also interrupts the interference, we expect that our scheme can have high tolerance of Δ as well. In Fig. 3, we plot fidelity F and cattiness Ca against \(\widetilde{\Delta }={\kappa }_{{{{{{\rm{R}}}}}}}\Delta /{g}^{2}\). Solid curves are plotted for γ = 0. Dashed curves are for γ = 2π × 3.0 MHz. The values of g, κR and κT are the same as in Fig. 2. In addition, the yellow curves are plotted for the single reflection model with |α|2 = 4. As for the multiple reflection model, the red curves are for |α|2 = 4, M = 5, the black curves are for |α|2 = 10, M = 20 and the blue curves are for |α|2 = 16, M = 100, respectively. As shown in Fig. 3, even for large |α|, as long as M is large, our scheme can be less sensitive to Δ. Moreover, since Δ does not induce optical losses, the responses of F and Ca to different M are consistent.

Fig. 3: Influence of atom-cavity detuning.
figure 3

a Fidelity F and (b) cattiness Ca versus dimensionless \(\widetilde{\Delta }={\kappa }_{{{{{{\rm{R}}}}}}}\Delta /{g}^{2}\) with g = 2π × 7.8 MHz and κR = κ = 2π × 2.3 MHz. The solid curves are plotted for γ = 0, and dashed curves are for γ = 2π × 3.0 MHz. The yellow curves represent the single reflection model with |α|2 = 4, while other curves are for the multiple reflection scheme.

Full size image

Effect of the atomic decoherence

Besides the atomic parameters γ and Δ, next we provide a discussion about the influence of the decoherence between the atomic states |↓〉 and |↑〉. Obviously, our scheme requires the atom to remain in superposition at least until the end of M cycles. Nevertheless, we need to mention that the multiple reflection processes hardly affect the atomic decoherence. In our scheme, when the atom is in |↑〉, the low atomic excitation probability can be satisfied. As for the atom in |↓〉, it is not coupled to the light field. We note that the atomic superposition state has been reported to last about 400 μs75,76, whereas the full-width at half-maximum of the light pulse that is employed in the experiment of single reflection model is 2.3 μs37. Therefore, it is possible for our scheme to be completed before the decoherence.

Effect of light loss caused by classical optical devices ε

So far, we have primarily discussed atomic parameters and optical losses due to atom (Type I loss). Next, we explore the impact of Type II loss, caused by classical optical devices, while keeping Type I light loss constant. We postulate that the loss rate per cycle outside the cavity is denoted by ε. Accordingly, the cumulative loss rate over the entire preparation process can be approximated as Mε, given that (1 − ε)M ≈ 1− Mε under the assumption of a small ε. Furthermore, considering the symmetrical of the optical devices on both arms of the interferometer, it is reasonable to assume that Type II loss is identical for each arm. Consequently, ε can be expressed as the sum of the light losses from each optical device located on a single arm of the interferometer. To facilitate our discussion, we assume that all optical devices are ideal, except for the switchable mirror SM (We also assume that irrespective of whether SM is turned on or off, its light loss rate remains constant). When coherent light |βz〉 incident upon SMz (z = 0,1), the reflected field is denoted as \(|\sqrt{1-\varepsilon }{\beta }_{z}\rangle\), and the lost light field can be represented as \(|\sqrt{\varepsilon }{\beta }_{z}\rangle\). In our simulation, the effect of these loss terms \(|\sqrt{\varepsilon }{\beta }_{z}\rangle\) from different cycles is accounted for by taking the trace, similar to our treatment of the cavity mentioned earlier.

In Fig. 4, we plot ε against effective fidelity Fef = Trloss{〈ψef|ψf〉}, cattiness Ca, and output intensity |αef|2 for different |α|2 and M. Here, Fef differs from F in that the target state is set as \(\left|{\psi }_{{{{{{\rm{ef}}}}}}}\right\rangle =\left(\left|{\alpha }_{{{{{{\rm{ef}}}}}}}\right\rangle \left|\uparrow \right\rangle +\left|-{\alpha }_{{{{{{\rm{ef}}}}}}}\right\rangle \left|\downarrow \right\rangle \right)/\sqrt{2}\) with αef = −C0↓ = α[(κR − κT)/(κT + κR)]M. Note that |C0↓〉 is the output when the atom is in |↓〉, where interference occurs between the two empty cavities. If the optical parameters of these two cavities are the same, only intensity of the output is affected and reduced from |α|2 to |αef|2. For the cavity-atom system, the parameters are set as g = 2π × 7.8 MHz, κR = 2π × 2.3 MHz, and γ = 2π × 3.0 MHz, aligning with actual cavity characteristics. However, for κT, we set it to zero. Based on the above parameters, the corresponding Type I loss is about 36.6%. Before we begin analyzing the impact of Type II light loss, it is important to note that the role of κT can be simulated with ε, since the main impact of κT is on the empty cavity light loss. This loss can be added to other Type II losses. Therefore, here we simply treat it as 0. Detailed explanations regarding κT are provided later.

Fig. 4: Influence of light loss caused by classical optical devices.
figure 4

a Effective fidelity Fef, (b) cattiness Ca, and (c) the output intensity |αef|2 versus ε with g = 2π × 7.8 MHz, γ = 2π × 3.0 MHz, κR = κ = 2π × 2.3 MHz, and Δ = 0. The yellow dotted-dashed curves represent the single reflection model with |α|2 = 4, and other curves represent the multiple reflection scheme with different |α|2 and M. The target state is \(\left(\left|{\alpha }_{{{{{{\rm{ef}}}}}}}\right\rangle \left|\uparrow \right\rangle +\left|-{\alpha }_{{{{{{\rm{ef}}}}}}}\right\rangle \left|\downarrow \right\rangle \right)/\sqrt{2}\).

Full size image

For comparison, we have also plotted the curves corresponding to the single reflection model with |α|2 = 4 (the yellow dotted-dashed curves). In this scenario, both Fef and Ca demonstrate minimal impact from ε, indicating that the key factor affecting the single reflection model here primarily stems from the optical losses in the individual atom-cavity system (Type I light loss). In this context, we utilize the yellow curve as a baseline to assess the quality of CS preparation in the multiple reflection model. From Fig. 4a, b, it can be observed that when ε is large, the multiple reflection model suffers from Type II light loss, with both Fef and Ca falling below that of the single reflection model. As M increases, the situation deteriorates further. However, as ε decreases, a dramatic shift occurs. Both Fef and Ca begin to outperform the single reflection case and rapidly increase. Smaller values of |α|2 and M exhibit a higher tolerance to Type II light loss, but larger M values can achieve greater maximal values of Fef and Ca (at ε = 0). As a result, there are observable intersections of curves for different M values for a given |α|2, which implies that it’s possible to obtain better fidelity using higher M. For larger values of |α|2, such improvements due to M are only noticeable when ε is closer to zero. All these observed effects are because that the impact of Type I losses gradually becomes dominant as ε approaches zero, and our method effectively suppresses the influence of Type I light loss. It’s important to recognize that in the single reflection model, Type I light losses can only be reduced through improvements in the atom-cavity system. In contrast, our multiple reflection approach, while not immune to light losses from classical optical devices, offers a method to reduce the stringent requirements on quantum microscopic system. This is the central and distinctive feature of our work.

To pave the way for the initiation of proof-of-concept experiments, we also provide two tables specifying the loss tolerances for classical optical devices in a single cycle. These loss tolerances are required to achieve certain levels of effective fidelity and cattiness under varying conditions of |α|2 and M. The tables reveal that, to achieve over 70% effective fidelity in conditions with |α|2 ≤ 4 and M ≤ 10, our scheme’s tolerance for Type II loss can be close to or even exceed 2%. For larger |α|2, however, our scheme requires much smaller ε. Hence, for our scheme, the constraint on preparing large-sized CS is tied to the quality of classical optical devices.

Discussion on the cavity parameter κ T and potential approaches to reduce light loss in empty cavity

Next, we provide additional explanation and clarification on the role of κT. We note that κT causes light loss when the atom is in either |↑〉 or |↓〉, thus affecting both the first and second types of light loss. However, when the atom is in |↑〉, according to Eqs. (3)–(4), and the fact that g > γ ≫ κT37, the loss caused by light field passing through the atom-cavity coupling system (Eq. (3)) is much smaller than the light loss caused by atomic scattering (Eq. (4)). As for Eq. (4), since κT ≪ κR, the influence of κT can be neglected. Hence, the Type I light loss due to κT is not our primary concern. In the scenario where the atom is in |↓〉 and does not participate in the interaction, the light transmission through the empty cavity falls under Type II light loss. In other words, the effect of κT can be accounted for in ε. According to Eq. (2), the light loss rate of the empty cavity after a single reflection is 1 − |(κT − κR)/(κT + κR)|2. In the experiment37, the cavity parameters are κT = 2π × 0.2 MHz and κR = 2π × 2.3 MHz, which results in ε ≈ 29% even if other optical devices are ideal, while after a few reflections, almost all photons are lost. Therefore, this cavity is unfortunately not suitable for our scheme. To reduce the optical losses, one needs either decrease κT or increase κR. The latter is simpler in practice. However, although increasing κR can reduce photon loss during the interference of two empty cavities (The atom is in state |↓〉), it also increases photon loss in the presence of atom-cavity coupling (The atom is in state |↑〉). To verify this, we plot Fig. 5 with |α|2 = 8, γ = 2π × 3.0 MHz, and Δ = 0. In Fig. 5a (for M = 10) and 5b (for M = 50), we plot the effective fidelity Fef against κR. Solid curves represent κT = 2π × 0.02 MHz, while dashed curves represent κT = 2π × 0.002 MHz. The corresponding light loss rate of the empty cavity is approximately 3.4% for κT = 2π × 0.02 MHz and 0.35% for κT = 2π × 0.002 MHz when κR = 2π × 2.3 MHz. Black curves are for g = 2π × 7.8 MHz, red for g = 2π × 15 MHz, and blue for g = 2π × 30 MHz. As for Fig. 5c, d, the green curves are plotted for |αef|2, while curves of other colors represent Ca. It is observed that Fef can be significantly improved as κT decreases. Regarding κR, as it initially increases, |αef|2 rapidly rises to its maximum value 8, which causes Fef to increase. Subsequently, photon loss due to atom-cavity coupling plays a major role, resulting in the decrease of Fef. Particularly, it’s noteworthy that for the black solid curve, when Fef starts to decrease, its corresponding |αef|2 is not close to 8. The reason is that κR is approaching the limit g2/γ. Under such limit, the photon loss of a single reflection on SSC1 when the atom is in |↑〉 is almost 100%. Therefore, we choose larger values of g to raise the limit so that the corresponding |αef|2 of maximum Fef can get closer to the maximum value 8, thereby increasing Fef. This phenomenon is verified in Fig. 5. Moreover, in the blue curves, κR maintains a wide range of high fidelity. This is due to relaxed constraint of g2 ≫ κRγ in our scheme. However, we must emphasize that achieving high fidelity does not necessarily require increasing g. By decreasing κT, we can achieve the same purpose. In fact, the motivation of this work is to reduce the influence of the atom, and to show that the performance of our protocol can be improved by just upgrading the classical optical system, such as the parameters κT and ε.

Fig. 5: Influence of cavity parameters.
figure 5

a, b Effective fidelity Fef, (c, d) cattiness Ca, and the output intensity |αef|2 versus κR with varying g, M, and κT in the multiple reflection model, where other parameters are set as |α|2 = 8, γ = 2π × 3.0 MHz, and Δ = 0. The target state is \(\left(\left|{\alpha }_{{{{{{\rm{ef}}}}}}}\right\rangle \left|\uparrow \right\rangle +\left|-{\alpha }_{{{{{{\rm{ef}}}}}}}\right\rangle \left|\downarrow \right\rangle \right)/\sqrt{2}\). Solid curves represent κT = 2π × 0.02 MHz, and dashed curves represent κT = 2π × 0.002 MHz. The green curves are plotted for |αef|2 only, while curves in other colors represent Fef and Ca. Black corresponds to g = 2π × 7.8 MHz, red to g = 2π × 15 MHz, and blue to g = 2π × 30 MHz.

Full size image

Regarding the impact of M, we provide a brief explanation here. When κR is small, significant Type II light loss leads to a decrease in our scheme’s performance with larger M values, as depicted in Fig. 5. However, as κR increases, leading to a decrease in Type II light loss, larger M values can ultimately offer improved Fef and Ca.

Discussion on pulse length and interferometer size

Based on the above analysis of various experimental parameters, we now discuss the requirements of our scheme for the duration of the incident pulse. It is noteworthy that the influence of the atom-cavity coupling system on the wave packet waveshape during a single reflection process has been discussed42. The results indicate that to shorten the pulse length by half, while maintaining the reflected waveshape unchanged is necessary to double κR. For the single reflection model, an increase in κR amplifies Type I losses, resulting in reduced fidelity, hence is not a favorable option. In our scheme, however, since Type I losses can be mitigated, increasing κR is feasible. For example, in the experiment37, the pulse duration is Tp = 2.3 μs, and the cavity parameter κR is 2π × 2.3 MHz. According to our simulations in Fig. 5, when |α|2 = 8, M = 50, κT = 2π × 0.002 MHz, and κR = 2π × 10 MHz, the effective fidelity of the output CS in our scheme is about 0.75. With κR increased by approximately 5 times, the pulse length used in our scheme can be shortened 5 times under the condition of keeping waveshape unchanged, i.e., to Tp ≈ 0.5 μs.

We, so far, stipulated that the waveshape of the reflected pulse remains unchanged. This is a requirement from the single reflection model, but not a necessity in our scheme. This is due to the fact that when the atom is in |↓〉, interference occurs between the two empty cavities, and even if the reflected waveshape distorts, it does not affect the interference process. Conversely, when the atom is in |↑〉, the role of the atom is merely to disrupt the interference. In this case, the light field is primarily concentrated on the empty cavity side, and the waveshape of the reflected pulse is still determined by the empty cavity reflection. Consequently, variations in the waveshape of the output pulse do not affect the generation of CS. This facilitates further compression of the pulse length in our scheme.

Next, we briefly discuss the size of the interferometer. If we define the size of the interferometer by the distance L between SM0 and SSC0, to ensure that the light-matter interaction in two cycles does not interfere with each other, it implies that L needs to be greater than the half pulse length, i.e., L ≥ (Tpc)/2, where c is the speed of light. Hence, the total flight distance of the pulse in the entire CS preparation process is MTpc. For a pulse duration Tp = 2.3 μs, L needs to be at least 350 m, and the total flight distance falls within the kilometer scale. Given such distances, employing optical fibers to construct the interferometer is a reasonable choice. Regarding the requirements for light loss from classical optical devices, one can refer to Tables 1 and 2 we provided. We note that the parameter κR in these tables is specified as 2π × 2.3 MHz. Increasing it allows us to further compress the pulse duration. For instance, setting κR to 2π × 10 MHz results in a pulse duration Tp of 0.5 μs, with minimum L adjusted to 75 m. By fixing other parameters at (g,γ) = 2π × (7.8, 3.0) MHz and κT = Δ = 0, along with using M = 20 and the best-reported optical fiber, which has an average attenuation of less than 0.157 dB km−177 (the corresponding Type II loss is about 0.53%), the effective fidelity of the output CS is about 0.77 for an input light field of |α|2 = 3. In this estimate, we have not yet accounted for other classical optical losses, such as those from SM and fiber-cavity coupling. If we set these additional losses to 2%, the effective fidelity reduces to 0.63. While our scheme can shift the source of errors from the atomic system to classical optical systems, it also demands higher manufacturing technology standards for existing optical devices.

Table 1 Impact of classical optical devices on fidelity
Full size table
Table 2 Impact of classical optical devices on cattiness
Full size table

Lastly, we address the requirements for the SM. In addition to light loss restrictions, there are also requirements for its response time Ts. One promising candidate of SM is Pockels cell65,66,67,68. Applying high voltage, it can rotate the polarization of the light field by 90 degrees, facilitating the extraction of the light field from the interferometer. Its response time is in the nanosecond range. Hence, Ts can be significantly shorter than the duration of the pulse Tp. Strictly speaking, to ensure that the transmission of the pulse is uninterrupted, the length of L should be (Tp + Ts)c/2, which means there needs to be a sufficient time window allowed for the change of state in the Pockels Cell. However, since Ts ≪ Tp, L is primarily determined by Tp.

Conclusions

We propose a method for generating macro-micro entanglement based on the interaction-free measurement and the quantum Zeno effect. Our method allows for the deterministic preparation of optical CS with arbitrarily large average photon numbers. Because only a small fraction of photons actually interacts with the quantum microsystem during multiple interactions, our method avoids directly exposing the quantum microsystem to a strong light field. This indirect control mechanism is a key feature of our work. Another significant feature of our work is the tolerance it shows for photon loss within the quantum microsystem. We show that the state |−α〉 is generated through multiple optical interferences, independent of the quantum microsystem. Conversely, the state |α〉 results from the disruption of the interference process, which remains feasible even if the quantum microsystem experiences substantial photon loss or other imperfections. This fact enables our scheme to improve the fidelity of the output CS through enhancements to the classical optical system.

Methods

System wave-function calculation

We have mentioned that a0 and a1 represent the annihilation operators of the light field in Zone 0 and Zone 1, respectively. Based on this, the function of BS can be described as \({a}_{0}^{{{\dagger}} }\to {a}_{0}^{{{\dagger}} }\cos \theta +{a}_{1}^{{{\dagger}} }\sin \theta\) and \({a}_{1}^{{{\dagger}} }\to {a}_{1}^{{{\dagger}} }\cos \theta -{a}_{0}^{{{\dagger}} }\sin \theta\) where θ = π/2M. Now, we consider an arbitrary initial photon state

$$\left|{{{{{\rm{Initial}}}}}}\right\rangle =\left|u,v\right\rangle =\exp \left(u{a}_{0}^{{{\dagger}} }-{u}^{* }{a}_{0}\right)\exp \left(v{a}_{1}^{{{\dagger}} }-{v}^{* }{a}_{1}\right)\left|0,0\right\rangle$$
(5)

which represents that a coherent state |u〉 is in Zone 0 and a coherent state |v〉 is in Zone 1. After passing through the BS, we have the final state

$$\left|{{{{{\rm{Final}}}}}}\right\rangle = \exp \left[u\left({a}_{0}^{{{\dagger}} }\cos \theta +{a}_{1}^{{{\dagger}} }\sin \theta \right)-{u}^{* }\left({a}_{0}\cos \theta +{a}_{1}\sin \theta \right)\right],\\ \times \exp \left[v\left({a}_{1}^{{{\dagger}} }\cos \theta -{a}_{0}^{{{\dagger}} }\sin \theta \right)-{v}^{* }\left({a}_{1}\cos \theta -{a}_{0}\sin \theta \right)\right]\left|{{{{\mathrm{0,0}}}}}\right\rangle \\ = \left|u\cos \theta -v\sin \theta ,u\sin \theta +v\cos \theta \right\rangle$$
(6)

Similarly, consider an arbitrary phase operation a† → eiφa†. For the initial state |Initial〉 = |u〉, after the operation, the final state is

$$\left|{{{{{\rm{Final}}}}}}\right\rangle =\exp \left(-\frac{1}{2}{|u}{|}^{2}\right){\sum }_{n=0}^{\infty }\frac{{u}^{n}}{\sqrt{n!}}\frac{1}{\sqrt{n!}}{\left({e}^{i\varphi }{a}^{{{\dagger}} }\right)}^{n}\left|0\right\rangle \\ =\exp \left(-\frac{1}{2}{{|}}u{{{|}}}^{2}\right)\mathop{\sum }_{n=0}^{{{\infty }}}\frac{1}{\sqrt{n!}}{\left(u{e}^{i\varphi }\right)}^{n}\left|n\right\rangle ={{|}}u{e}^{i\varphi }{{\rangle }}$$
(7)

Based on Eqs. (6) and (7), we provide the calculation of Eq. (1).

At the beginning of the preparation, the wave-function of the whole system is

$$\left|{\psi }^{\left(0\right)}\right\rangle =\frac{\sqrt{2}}{2}\left|\alpha ,0\right\rangle \left(\left|\uparrow \right\rangle +\left|\downarrow \right\rangle \right)$$
(8)

In the first cycle, after the photons pass through BS for the first time, the system state is

$$\left|{\psi }^{(1)}\right\rangle =\frac{\sqrt{2}}{2}\left|\alpha \cos \theta ,\alpha \sin \theta \right\rangle \left(\left|\uparrow \right\rangle +\left|\downarrow \right\rangle \right)$$
(9)

Before the photons are reflected by SSC, the system state becomes \(\frac{\sqrt{2}}{2}\left|-\alpha \cos \theta ,-\alpha \sin \theta \right\rangle \left(\left|\uparrow \right\rangle +\left|\downarrow \right\rangle \right)\) due to PS. Regarding the reflection, we emphasize that only when the atom is in |↑〉, SSC1 does not change the phase of the reflected field. As a result, the wave function of the whole system becomes \(\frac{\sqrt{2}}{2}\left|\alpha \cos \theta ,-\alpha \sin \theta \right\rangle \left|\uparrow \right\rangle +\frac{\sqrt{2}}{2}\left|\alpha \cos \theta , \alpha \sin \theta \right\rangle \left|\downarrow \right\rangle\). Subsequently, after the second time that the photons pass through BS, we have

$$\left|{\psi }^{(2)}\right\rangle =\frac{\sqrt{2}}{2}\left|\alpha ,0\right\rangle \left|\uparrow \right\rangle +\frac{\sqrt{2}}{2}\left|\alpha \cos 2\theta ,\alpha \sin 2\theta \right\rangle \left|\downarrow \right\rangle$$
(10)

This state becomes the initial state of the second cycle, and the process is repeated. It is not difficult to obtain that after m cycles, the wave-function of the whole system is

$$\left|{\psi }^{\left(2m\right)}\right\rangle =\frac{\sqrt{2}}{2}\left|\alpha ,0\right\rangle \left|\uparrow \right\rangle +\frac{\sqrt{2}}{2}\left|\alpha \cos 2m\theta ,\alpha \sin 2m\theta \right\rangle \left|\downarrow \right\rangle$$
(11)

Here the superscript of |ψ(2m)〉 represents the photons pass through BS 2m times.

Input-output theory for the atom-cavity coupling system

The Hamiltonian of cavity-atom system (SSC1) can be described as

$$H= \;{\hslash \omega }_{{{{{{\rm{e}}}}}}}{\sigma }_{{{{{{\rm{ee}}}}}}}+\hslash {\omega }_{\uparrow }{\sigma }_{\uparrow \uparrow }+\hslash {\omega }_{{{{{{\rm{c}}}}}}}{a}^{{{\dagger}} }a+\hslash {\sum }_{J={{{{{\rm{R}}}}}},{{{{{\rm{T}}}}}},{{{{{\rm{S}}}}}}}{\int }_{-\infty }^{\infty }{\omega }_{J}{b}_{J}^{{{\dagger}} }({\omega }_{J}){b}_{J}({\omega }_{J})d{\omega }_{J} \\ +\hslash g\left({\sigma }_{\uparrow {{{{{\rm{e}}}}}}}{a}^{{{\dagger}} }+{\sigma }_{{{{{{\rm{e}}}}}}\uparrow }a\right)+\hslash \sqrt{\frac{\gamma }{{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }\left[{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}{b}_{{{{{{\rm{S}}}}}}}^{{{\dagger}} }({\omega }_{{{{{{\rm{S}}}}}}})+{\sigma }_{{{{{{\rm{e}}}}}}\uparrow }{b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}})\right]d{\omega }_{{{{{{\rm{S}}}}}}}\\ +{{{{{\rm{i}}}}}}\hslash \sqrt{\frac{{\kappa }_{R}}{{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }\left[a{b}_{{{{{{\rm{R}}}}}}}^{{{\dagger}} }\left({\omega }_{{{{{{\rm{R}}}}}}}\right)-{a}^{{{\dagger}} }{b}_{{{{{{\rm{R}}}}}}}({\omega }_{{{{{{\rm{R}}}}}}})\right]d{\omega }_{{{{{{\rm{R}}}}}}}\\ +{{{{{\rm{i}}}}}}\hslash \sqrt{\frac{{\kappa }_{T}}{{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }\left[a{b}_{{{{{{\rm{T}}}}}}}^{{{\dagger}} }\left({\omega }_{{{{{{\rm{T}}}}}}}\right)-{a}^{{{\dagger}} }{b}_{{{{{{\rm{T}}}}}}}({\omega }_{{{{{{\rm{T}}}}}}})\right]d{\omega }_{{{{{{\rm{T}}}}}}}$$
(12)

where ℏωe is the energy of excited atomic state |e〉, ℏω↑ is the energy of the atomic state |↑〉, ωc is the frequency of the cavity mode described by annihilation operator \(a\), ωJ is the frequency of external field described by annihilation operator b(ωJ = R,T,S) with \(\left[{b}_{J}({\omega }_{J}),{b}_{J}^{{{\dagger}} }({\omega }_{J}^{{\prime} })\right]=\delta ({\omega }_{J}-{\omega }_{J}^{{\prime} })\), and the subscript \({{{{{\rm{R}}}}}}\) represents the external multi-mode field on CMR side, \({{{{{\rm{T}}}}}}\) represents the external field on CMT side, S represents the scattering field due to the atomic spontaneous emission. In addition, \(g\) is coupling constant between the cavity and the atomic transition between |e〉 and |↑〉, 2γ is the spontaneous atomic decay rate on the same transition, κR and κT are cavity field decay rates. We also set that σ↑e = |↑〉〈e|, σee = |e〉〈e| and σ↑↑ = |↑〉〈↑|.

Based on the above Hamiltonian, it is not difficult to obtain the following Heisenberg equations

$$\frac{{da}(t)}{{dt}}=-{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{c}}}}}}}a(t)-{{{{{\rm{i}}}}}}g{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}(t)-{\sum }_{J={{{{{\rm{R}}}}}},{{{{{\rm{T}}}}}}}\sqrt{\frac{{\kappa }_{J}}{{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }{b}_{J}({\omega }_{J},t)d{\omega }_{J}$$
(13)
$$\frac{d}{{dt}}{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}(t)=-{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }\right){\sigma }_{\uparrow {{{{{\rm{e}}}}}}}(t)+{{{{{\rm{i}}}}}}g\left[{\sigma }_{{{{{{\rm{ee}}}}}}}\left(t\right)-{\sigma }_{\uparrow \uparrow }\left(t\right)\right]a(t)$$
$$+{{{{{\rm{i}}}}}}\sqrt{\frac{\gamma }{{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }\left[{\sigma }_{{{{{{\rm{ee}}}}}}}(t)-{\sigma }_{\uparrow \uparrow }(t)\right]{b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}},t)d{\omega }_{{{{{{\rm{S}}}}}}}$$
$$\approx -{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }\right){\sigma }_{\uparrow {{{{{\rm{e}}}}}}}(t)-{{{{{\rm{i}}}}}}{ga}(t)-{{{{{\rm{i}}}}}}\sqrt{\frac{\gamma }{{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }{b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}},t)d{\omega }_{{{{{{\rm{S}}}}}}}$$
(14)

In the approximation, we have assumed that37,45,72

$$\left\langle \left({\sigma }_{{{{{{\rm{ee}}}}}}}-{\sigma }_{\uparrow \uparrow }\right)a\right\rangle =-\left\langle a\right\rangle$$
(15)

which indicates that the atom stays in the state |↑〉 most of the time. This can be satisfied when the input is weak.

In addition, we can also obtain Heisenberg equations for \(b(\omega )\). They are

$$\frac{d{b}_{J}({\omega }_{J},t)}{{dt}}=-{{{{{\rm{i}}}}}}{\omega }_{J}{b}_{J}\left({\omega }_{J},t\right)+\sqrt{\frac{{\kappa }_{R}}{{{{{{\rm{\pi }}}}}}}}a\left(t\right),J={{{{{\rm{R}}}}}},{{{{{\rm{T}}}}}}$$
(16)
$$\frac{d{b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}},t)}{{dt}}=-{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{S}}}}}}}{b}_{{{{{{\rm{S}}}}}}}\left({\omega }_{{{{{{\rm{S}}}}}}},t\right)-{{{{{\rm{i}}}}}}\sqrt{\frac{\gamma }{{{{{{\rm{\pi }}}}}}}}{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)$$
(17)

Equations (16) and (17) can be rewritten in integral form. If we assume that the atom-light interaction begins at time Tin < t, we have

$${b}_{J}({\omega }_{J},t)={b}_{J}({\omega }_{J},{T}_{{{{{{\rm{in}}}}}}}){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{J}({T}_{{{{{{\rm{in}}}}}}}-t)}+\sqrt{\frac{{\kappa }_{J}}{{{{{{\rm{\pi }}}}}}}}{\int }_{{T}_{{{{{{\rm{in}}}}}}}}^{t}a({t}^{{\prime} }){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{J}({t}^{{\prime} }-t)}d{t}^{{\prime} }$$
(18)
$${b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}},t)={b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}},{T}_{{{{{{\rm{in}}}}}}}){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{S}}}}}}}({T}_{{{{{{\rm{in}}}}}}}-t)}-{{{{{\rm{i}}}}}}\sqrt{\frac{\gamma }{{{{{{\rm{\pi }}}}}}}}{\int }_{{T}_{{{{{{\rm{in}}}}}}}}^{t}{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}({t}^{{\prime} }){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{S}}}}}}}({t}^{{\prime} }-t)}d{t}^{{\prime} }$$
(19)

If we assume that the atom-light interaction ends at time Tout > t, we have

$${b}_{J}({\omega }_{J},t)={b}_{J}({\omega }_{J},{T}_{{{{{{\rm{out}}}}}}}){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{J}({T}_{{{{{{\rm{out}}}}}}}-t)}-\sqrt{\frac{{\kappa }_{J}}{{{{{{\rm{\pi }}}}}}}}{\int }_{t}^{{T}_{{{{{{\rm{out}}}}}}}}a({t}^{{\prime} }){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{J}({t}^{{\prime} }-t)}d{t}^{{\prime} }$$
(20)
$${b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}},t)={b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}},{T}_{{{{{{\rm{out}}}}}}}){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{S}}}}}}}({T}_{{{{{{\rm{out}}}}}}}-t)}+{{{{{\rm{i}}}}}}\sqrt{\frac{\gamma }{{{{{{\rm{\pi }}}}}}}}{\int }_{t}^{{T}_{{{{{{\rm{out}}}}}}}}{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}({t}^{{\prime} }){e}^{i{\omega }_{{{{{{\rm{S}}}}}}}({t}^{{\prime} }-t)}d{t}^{{\prime} }$$
(21)

By integrating Eq. (18) with frequency, it is not difficult to obtain that

$$\sqrt{\frac{{\kappa }_{J}}{\pi }}\int\nolimits_{-\infty }^{\infty }{b}_{J}({\omega }_{J},t)d{\omega }_{J}$$
$$= \sqrt{\frac{{\kappa }_{J}}{\pi }}\int\nolimits_{-\infty }^{\infty }{b}_{J}({\omega }_{J},{T}_{{{{{{\rm{in}}}}}}}){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{J}({T}_{{{{{{\rm{in}}}}}}}-t)}d{\omega }_{J}\\ +2{\kappa }_{J}\underset{{T}_{{{{{{\rm{in}}}}}}}}{\overset{t}{\int }}a({t}^{{\prime} })d{t}^{{\prime} }\frac{1}{2{{{{{\rm{\pi }}}}}}}\int\nolimits_{-\infty }^{\infty }{{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{J}({t}^{{\prime} }-t)}d{\omega }_{J}$$
$$=\sqrt{2{\kappa }_{J}}{a}_{J,{{{{{\rm{in}}}}}}}\left(t\right)+{\kappa }_{J}a\left(t\right)$$
(22)

where we have used the relation74

$${\int }_{{t}_{0}}^{t}f({t}^{{\prime} })\delta (t-{t}^{{\prime} })d{t}^{{\prime} }={\int }_{t}^{{t}_{1}}f({t}^{{\prime} })\delta (t-{t}^{{\prime} })d{t}^{{\prime} }=\frac{1}{2}f\left(t\right),({t}_{0}\, < \, t\, < \, {t}_{1}),$$
(23)

and the assumptions (J = R,T)

$${a}_{J,{{{{{\rm{in}}}}}}}\left(t\right)=\frac{1}{\sqrt{2{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }{b}_{J}\left({\omega }_{J},{T}_{{{{{{\rm{in}}}}}}}\right){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{J}\left({T}_{{{{{{\rm{in}}}}}}}-t\right)}d{\omega }_{J}$$
(24)
$${a}_{J,{out}}\left(t\right)=\frac{1}{\sqrt{2{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }{b}_{J}\left({\omega }_{J},{T}_{{{{{{\rm{out}}}}}}}\right){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{J}\left({T}_{{{{{{\rm{out}}}}}}}-t\right)}d{\omega }_{J}$$
(25)
$${a}_{{{{{{\rm{S}}}}}},{{{{{\rm{in}}}}}}}\left(t\right)=\frac{1}{\sqrt{2{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }{b}_{{{{{{\rm{S}}}}}}}\left({\omega }_{{{{{{\rm{S}}}}}}},{T}_{{{{{{\rm{in}}}}}}}\right){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{S}}}}}}}\left({T}_{{{{{{\rm{in}}}}}}}-t\right)}d{\omega }_{{{{{{\rm{S}}}}}}}$$
(26)
$${a}_{{{{{{\rm{S}}}}}},{{{{{\rm{out}}}}}}}\left(t\right)=\frac{1}{\sqrt{2{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }{b}_{{{{{{\rm{S}}}}}}}\left({\omega }_{{{{{{\rm{S}}}}}}},{T}_{{{{{{\rm{out}}}}}}}\right){{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{S}}}}}}}\left({T}_{{{{{{\rm{out}}}}}}}-t\right)}d{\omega }_{{{{{{\rm{S}}}}}}}$$
(27)

Similarly, from Eqs. (19)–(21), we have

$$\sqrt{\frac{\gamma }{{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }{b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}},t)d{\omega }_{{{{{{\rm{S}}}}}}}=\sqrt{2\gamma }{a}_{{{{{{\rm{S}}}}}},{{{{{\rm{in}}}}}}}\left(t\right)-{{{{{\rm{i}}}}}}\gamma {\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)$$
(28)
$$\sqrt{\frac{{\kappa }_{J}}{\pi }}{\int }_{-\infty }^{\infty }{b}_{J}({\omega }_{J},t)d{\omega }_{J}=\sqrt{2{\kappa }_{J}}{a}_{J,{{{{{\rm{out}}}}}}}\left(t\right)-{\kappa }_{J}a\left(t\right)$$
(29)
$$\sqrt{\frac{\gamma }{{{{{{\rm{\pi }}}}}}}}{\int }_{-\infty }^{\infty }{b}_{{{{{{\rm{S}}}}}}}({\omega }_{{{{{{\rm{S}}}}}}},t)d{\omega }_{{{{{{\rm{S}}}}}}}=\sqrt{2\gamma }{a}_{{{{{{\rm{S}}}}}},{{{{{\rm{out}}}}}}}\left(t\right)+{{{{{\rm{i}}}}}}\gamma {\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)$$
(30)

Then, by substituting Eq. (22) and (29) into (13), we can obtain the dynamic equations

$$\frac{{da}(t)}{{dt}}=-{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{c}}}}}}}a\left(t\right)-{{{{{\rm{i}}}}}}g{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)-\sqrt{2{\kappa }_{{{{{{\rm{R}}}}}}}}{a}_{{{{{{\rm{R}}}}}},{{{{{\rm{in}}}}}}}\left(t\right)-{\kappa }_{{{{{{\rm{R}}}}}}}a\left(t\right)-\sqrt{2{\kappa }_{{{{{{\rm{T}}}}}}}}{a}_{{{{{{\rm{T}}}}}},{{{{{\rm{in}}}}}}}\left(t\right)-{\kappa }_{{{{{{\rm{T}}}}}}}a\left(t\right)$$
(31)
$$\frac{{da}(t)}{{dt}}=-{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{c}}}}}}}a\left(t\right)-{{{{{\rm{i}}}}}}g{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)-\sqrt{2{\kappa }_{{{{{{\rm{R}}}}}}}}{a}_{{{{{{\rm{R}}}}}},{{{{{\rm{out}}}}}}}\left(t\right)+{\kappa }_{{{{{{\rm{R}}}}}}}a\left(t\right)-\sqrt{2{\kappa }_{{{{{{\rm{T}}}}}}}}{a}_{{{{{{\rm{T}}}}}},{{{{{\rm{in}}}}}}}\left(t\right)-{\kappa }_{{{{{{\rm{T}}}}}}}a\left(t\right)$$
(32)
$$\frac{{da}(t)}{{dt}}=-{{{{{\rm{i}}}}}}{\omega }_{{{{{{\rm{c}}}}}}}a\left(t\right)-{{{{{\rm{i}}}}}}g{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)-\sqrt{2{\kappa }_{{{{{{\rm{R}}}}}}}}{a}_{{{{{{\rm{R}}}}}},{{{{{\rm{in}}}}}}}\left(t\right)-{\kappa }_{{{{{{\rm{R}}}}}}}a\left(t\right)-\sqrt{2{\kappa }_{{{{{{\rm{T}}}}}}}}{a}_{{{{{{\rm{T}}}}}},{{{{{\rm{out}}}}}}}\left(t\right)+{\kappa }_{{{{{{\rm{T}}}}}}}a\left(t\right)$$
(33)

By substituting Eq. (28, 30) into (14), we have

$$\frac{d}{{dt}}{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)=-{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }\right){\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)-{{{{{\rm{i}}}}}}{ga}\left(t\right)-{{{{{\rm{i}}}}}}\sqrt{2\gamma }{a}_{{{{{{\rm{S}}}}}},{{{{{\rm{in}}}}}}}\left(t\right)-\gamma {\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)$$
(34)
$$\frac{d}{{dt}}{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)=-{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }\right){\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)-{{{{{\rm{i}}}}}}{ga}\left(t\right)-{{{{{\rm{i}}}}}}\sqrt{2\gamma }{a}_{{{{{{\rm{S}}}}}},{{{{{\rm{out}}}}}}}\left(t\right)+\gamma {\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)$$
(35)

In the following, we assume that only the input on CMR side is none-zero, i.e., \({a}_{{{{{{\rm{T}}}}}},{{{{{\rm{in}}}}}}}(t)={a}_{{{{{{\rm{S}}}}}},{{{{{\rm{in}}}}}}}(t)=0\). Then, by subtracting (31) and (32), we can get the relation between the input \({a}_{{{{{{\rm{R}}}}}},{{{{{\rm{in}}}}}}}(t)\) and output \({a}_{{{{{{\rm{R}}}}}},{{{{{\rm{out}}}}}}}(t)\),

$${a}_{{{{{{\rm{R}}}}}},{{{{{\rm{in}}}}}}}\left(t\right)+\sqrt{2{\kappa }_{{{{{{\rm{R}}}}}}}}a\left(t\right)={a}_{{{{{{\rm{R}}}}}},{{{{{\rm{out}}}}}}}\left(t\right)$$
(36)

By subtracting (31) and (33), we have

$${a}_{{{{{{\rm{T}}}}}},{{{{{\rm{out}}}}}}}\left(t\right)=\sqrt{2{\kappa }_{{{{{{\rm{T}}}}}}}}a\left(t\right)$$
(37)

By subtracting (34) and (35), we have

$${a}_{{{{{{\rm{S}}}}}},{{{{{\rm{out}}}}}}}\left(t\right)=-{{{{{\rm{i}}}}}}\sqrt{2\gamma }{\sigma }_{\uparrow {{{{{\rm{e}}}}}}}\left(t\right)$$
(38)

In addition to the above relations, we next calculate the steady-state solution of the dynamic Eq. (31, 32, 34) by assuming that the cavity-atom system is driven by the input light field with frequency ω. We suppose that

$${a}_{{{{{{\rm{R}}}}}},{{{{{\rm{in}}}}}}}(t)={\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }{{{{{{\rm{e}}}}}}}^{-{{{{{\rm{i}}}}}}\omega t},$$
$$a(t)=\alpha {{{{{{\rm{e}}}}}}}^{-{{{{{\rm{i}}}}}}\omega t},$$
$${\sigma }_{\uparrow {{{{{\rm{e}}}}}}}(t)=\widetilde{\sigma }{{{{{{\rm{e}}}}}}}^{-{{{{{\rm{i}}}}}}\omega t},$$
$${a}_{{{{{{\rm{R}}}}}},{{{{{\rm{out}}}}}}}(t)={\alpha }_{{{{{{\rm{R}}}}}},1\uparrow }{{{{{{\rm{e}}}}}}}^{-{{{{{\rm{i}}}}}}\omega t},$$
$${a}_{{{{{{\rm{T}}}}}},{{{{{\rm{out}}}}}}}(t)={\alpha }_{{{{{{\rm{T}}}}}},1\uparrow }{{{{{{\rm{e}}}}}}}^{-{{{{{\rm{i}}}}}}\omega t},$$
$${a}_{{{{{{\rm{S}}}}}},{{{{{\rm{out}}}}}}}\left(t\right)={\alpha }_{{{{{{\rm{S}}}}}},1\uparrow }{{{{{{\rm{e}}}}}}}^{-{{{{{\rm{i}}}}}}\omega t}$$
(39)

Then, we can obtain that

$$\left[-{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{c}}}}}}}-\omega \right)-{\kappa }_{{{{{{\rm{R}}}}}}}-{\kappa }_{{{{{{\rm{T}}}}}}}\right]\alpha -{{{{{\rm{i}}}}}}g\widetilde{\sigma }-\sqrt{2{\kappa }_{{{{{{\rm{R}}}}}}}}{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }=0$$
(40)
$$\left[-{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{c}}}}}}}-\omega \right)+{\kappa }_{{{{{{\rm{R}}}}}}}-{\kappa }_{{{{{{\rm{T}}}}}}}\right]\alpha -{{{{{\rm{i}}}}}}g\widetilde{\sigma }-\sqrt{2{\kappa }_{{{{{{\rm{R}}}}}}}}{\alpha }_{{{{{{\rm{R}}}}}},1\uparrow }=0$$
(41)
$$\left[-{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }-\omega \right)-\gamma \right]\widetilde{\sigma }-{{{{{\rm{i}}}}}}g\alpha =0$$
(42)

It is not difficult to get that

$${\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }=-\frac{\left[{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{c}}}}}}}-\omega \right)+{\kappa }_{{{{{{\rm{R}}}}}}}+{\kappa }_{{{{{{\rm{T}}}}}}}\right]\left[{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }-\omega \right)+\gamma \right]+{g}^{2}}{\sqrt{2{\kappa }_{{{{{{\rm{R}}}}}}}}\left[{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }-\omega \right)+\gamma \right]}\alpha$$
(43)
$${\alpha }_{{{{{{\rm{R}}}}}},1\uparrow }=-\frac{\left[{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{c}}}}}}}-\omega \right)-{\kappa }_{{{{{{\rm{R}}}}}}}+{\kappa }_{{{{{{\rm{T}}}}}}}\right]\left[{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }-\omega \right)+\gamma \right]+{g}^{2}}{\sqrt{2{\kappa }_{{{{{{\rm{R}}}}}}}}\left[{{{{{\rm{i}}}}}}\left({\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }-\omega \right)+\gamma \right]}\alpha$$
(44)

Equation (43) shows that when the input increases, the intensity of the cavity field also increase, resulting in the condition Eq. (15) not being satisfied.

With Eqs. (43) and (44), we can calculate Eq. (2). Suppose that the cavity and the external field are resonant, i.e., \(\omega ={\omega }_{{{{{{\rm{c}}}}}}}\), and \(\Delta ={\omega }_{{{{{{\rm{e}}}}}}}-{\omega }_{\uparrow }-{\omega }_{{{{{{\rm{c}}}}}}}\equiv {\omega }_{{{{{{\rm{a}}}}}}}-{\omega }_{{{{{{\rm{c}}}}}}}\), we obtain

$$\frac{{\alpha }_{{{{{{\rm{R}}}}}},1\uparrow }}{{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }}=1-\frac{2{\kappa }_{{{{{{\rm{R}}}}}}}\left({{{{{\rm{i}}}}}}\Delta +\gamma \right)}{\left({\kappa }_{{{{{{\rm{R}}}}}}}+{\kappa }_{{{{{{\rm{T}}}}}}}\right)\left({{{{{\rm{i}}}}}}\Delta +\gamma \right)+{g}^{2}}$$
(45)

By using Eqs. (37) and (38), we can also have Eqs. (3) and (4), which are

$$\frac{{\alpha }_{{{{{{\rm{T}}}}}},1\uparrow }}{{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }}=-\frac{2\sqrt{{\kappa }_{{{{{{\rm{R}}}}}}}{\kappa }_{{{{{{\rm{T}}}}}}}}\left({{{{{\rm{i}}}}}}\Delta +\gamma \right)}{\left({\kappa }_{{{{{{\rm{R}}}}}}}+{\kappa }_{{{{{{\rm{T}}}}}}}\right)\left({{{{{\rm{i}}}}}}\Delta +\gamma \right)+{g}^{2}}$$
(46)
$$\frac{{\alpha }_{{{{{{\rm{S}}}}}},1\uparrow }}{{\alpha }_{{{{{{\rm{i}}}}}},1\uparrow }}=\frac{2\sqrt{{\kappa }_{{{{{{\rm{R}}}}}}}\gamma }g}{\left({\kappa }_{{{{{{\rm{R}}}}}}}+{\kappa }_{{{{{{\rm{T}}}}}}}\right)\left({{{{{\rm{i}}}}}}\Delta +\gamma \right)+{g}^{2}}$$
(47)

Cattiness calculation

Taking into account all possible light losses, the final state of the system after M cycles can be expressed as \(|{\psi }_{{{{{{\rm{f}}}}}}}\rangle =\frac{1}{\sqrt{2}}(|{C}_{0\uparrow }\rangle |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow }\rangle |\uparrow \rangle +|{C}_{0\downarrow }\rangle |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\downarrow }\rangle |\downarrow \rangle )=\frac{1}{\sqrt{2}}[\frac{1}{\sqrt{2}}(|\uparrow \rangle +|\downarrow \rangle )|{\psi }_{0}\rangle +\frac{1}{\sqrt{2}}(|\uparrow \rangle -|\downarrow \rangle )|{\psi }_{1}\rangle ]\). After measuring the atom, the light field collapses to state \(|{\psi }_{c=0,1}\rangle =\frac{1}{\sqrt{2}}(|{C}_{0\uparrow }\rangle |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow }\rangle +{(-1)}^{c}|{C}_{0\downarrow }\rangle |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\downarrow }\rangle )\) with equal probability. Its corresponding density matrix is denoted as \(\left|{\psi }_{c}\right\rangle \left\langle {\psi }_{c}\right|\). By tracing over the loss terms, the resulting reduced dsensity matrix is obtained, represented as

$$\rho =T{r}_{{{{{{\rm{loss}}}}}}}\big\{\big|{\psi }_{c}\big \rangle \big \langle {\psi }_{c}\big |\big\}=\frac{1}{2}\big|{C}_{0\uparrow }\big \rangle \big \langle {C}_{0\uparrow }\big |+\frac{1}{2}\big |{C}_{0\downarrow }\big \rangle \big \langle {C}_{0\downarrow }\big |$$
$$+{(-1)}^{c}\frac{1}{2}\big \langle {{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\downarrow }\big |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow }{{\big\rangle }}\big |{C}_{0\uparrow }\big \rangle \big \langle {C}_{0\downarrow }\big |+{(-1)}^{c}\frac{1}{2}\big \langle {{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow }\big |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\downarrow }{{\big \rangle }}\big |{C}_{0\downarrow }\big \rangle \big \langle {C}_{0\uparrow }\big |$$
(48)

By substituting \(\rho\) into the definition of cattiness69,70,71

$${C}_{{{{{{\rm{a}}}}}}}=-{Tr}\left[\rho \cdot L\left(\rho \right)\right]$$
(49)

with \(L(\rho )=a\rho {a}^{+}-\frac{1}{2}\rho {a}^{+}a-\frac{1}{2}{a}^{+}a\rho\), we can obtain that

$${C}_{{{{{{\rm{a}}}}}}}=-\mathop{\sum }_{\nu =0}^{\infty }\left\langle \nu \right|\rho a\rho {a}^{+}\left|\nu \right\rangle +\mathop{\sum }_{\nu =0}^{\infty }\nu \left\langle \nu \right|{\rho }^{2}\left|\nu \right\rangle$$
(50)

where \(\left|v\right\rangle\) represents Fock state. Utilizing the following expressions (\(j=\uparrow ,\downarrow\)),

$$\left\langle v\right|{C}_{0j}{{\rangle }}=\left\langle v\right|{{{{{{\rm{e}}}}}}}^{-\frac{{{|}}{C}_{0j}{{{|}}}^{2}}{2}}\mathop{\sum }_{u=0}^{\infty }\frac{{C}_{0j}^{u}}{\sqrt{u!}}\left|u\right\rangle ={{{{{{\rm{e}}}}}}}^{-\frac{{{|}}{C}_{0j}{{{|}}}^{2}}{2}}\frac{{C}_{0j}^{v}}{\sqrt{v!}}$$
(51)

we have

$${C}_{{{{{{\rm{a}}}}}}}=\frac{1}{4}\left({{{\big |}}\big\langle {{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow }\big |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\downarrow }{{\big \rangle }}{{\big |}}}^{2}-{{{\big |}}\big \langle {C}_{0\uparrow }\big|{C}_{0\downarrow }{{\big\rangle }}{{\big |}}}^{2}\right){{{\big |}}{C}_{0\uparrow }-{C}_{0\downarrow }{{\big |}}}^{2}$$
(52)

For comparison, we also give the expression for fidelity here, which is

$$F=\frac{1}{4}\left\{{{{\big |}}\big\langle \alpha \big|{C}_{0\uparrow }{{\big \rangle }}{{\big |}}}^{2}+{{{\big |}}\big \langle -\alpha \big |{C}_{0\downarrow }{{\big \rangle }}{{\big |}}}^{2}+2{{{{\mathrm{Re}}}}}\left[\big \langle \alpha \big |{C}_{0\uparrow }{{\big \rangle }}\big \langle {C}_{0\downarrow }\big |-\alpha \big \rangle \big \langle {{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\downarrow }\big |{{{{{\rm{los}}}}}}{{{{{{\rm{s}}}}}}}_{\uparrow }{{\big \rangle }}\right]\right\}$$
(53)

It can be easily seen that the fidelity is related to |〈loss↑|loss↓〉|, while the cattiness is related to |〈loss↑|loss↓〉|2, and thus is more sensitive to light loss.