Introduction

In the event of an emerging disease, public health officials are tasked with identifying the geographic spread and time course of the outbreak and identifying the most effective utilization of available health interventions and resources to mitigate disease outcomes. In addition to the natural history and biology of the disease, the demographic characteristics of the population at risk play an important role in determining the pattern of epidemic spread and identifying the type and intensity of public health intervention measures required for disease control1,2,3. Furthermore, the differential prevalence of predisposing health conditions and other types of health disparities increases uncertainty about how a novel disease would affect different populations with distinctly different mobility patterns, social interactions and health characteristics4. The importance of these factors in influencing disease burden was highlighted during outbreaks of the 2009 H1N1 pandemic in several Canadian population settings, including First Nation reserves in northern Manitoba, remote and isolated communities in Nunavut and Aboriginal communities on Vancouver Island5,6,7.

Understanding the interplay between demographic, health, infection and control parameters requires the development of a modeling framework that can identify individuals with their assigned information and describe disease spread in the population in silico (i.e., via computer simulations). Agent-based models, which specifically encapsulate individual-level characteristics, behaviors and population profiles, provide such a framework that is capable of reproducing observed scenarios in epidemics and exploring plausible contingency plans and control measures for curtailing an emerging disease8,9. Agent based modeling typically uses a bottom-up approach in which complex phenomena emerge from interactions between autonomous entities (i.e., agents) that perceive, make decisions and act within an environment.

Here we develop an agent-based model to investigate the role of demographic variables on disease dynamics. Specifically, we wish to qualitatively study the extent to which population age structure and household composition influence disease propagation. For the purpose of this investigation, the spread of influenza in a remote and isolated community is modeled and the effects of changes in three important variables are explored: (i) age distribution; (ii) household size; and (iii) the level of pre-existing immunity in the population. Furthermore, we investigate the effect of reactive short-duration school closures on reducing in the epidemic size and attack rates in different age groups in the population.

Results

We simulated the model to investigate the effect of shifting age distributions and household compositions on the clinical attack rates (the proportion of population infected clinically throughout the epidemic) as a function of pre-existing immunity levels p1 and p2 for individuals above and below 50 years of age, respectively. These pre-existing immunity levels remain constant throughout each simulation scenario in their respective ranges. The results presented here are based on averaging 1000 simulation runs in each scenario. Simulations with no secondary cases following the introduction of a primary infection were rejected and re-run with a different random number seed.

Demographic profiles of a remote and isolated community (RC) in northern Manitoba and Winnipeg as the largest urban center in Manitoba, are used and referred to for comparison. Age distributions used for the experiments either resemble RC (Figure 1a) or are Winnipeg-like (Figure 1c). Although not the focus of this work, employment characteristics of Winnipeg were also considered for adding more realism when using the Winnipeg-like age distribution. We explored three scenarios for household composition: RC (Figure 1b); Winnipeg-like (Figure 1d); and households of size 4 and 5. The latter was considered for redistributing individuals amongst existing number of private dwellings to minimize the maximum household size. Since the average number of persons per household in RC is 4.35, this strategy will result in households of size 4 and 5. The population of RC was fixed in all scenarios, but the number of dwellings, originally 436, changed to 795 to simulate Winnipeg-like household composition. Furthermore, using the original demographics of RC, we simulated a 4-week and an 8-week school closure scenario following identification of an infectious case in the school-age group. For each simulation scenario, the ranges of immunity levels p1 and p2 are switched to explore, by analogy, the prioritization of protective measures for younger individuals as a public health policy. Experiments are summarized in Table 1 and further details of each simulated scenario are provided in the Supplementary Information.

Table 1 Summary of experiments.
Full size table
Figure 1
figure 1

Population age distributions (dark grey) and number of persons per household (light grey) for RC (a,b) and Winnipeg (c,d)10,11,25.

Full size image

Age distribution shift

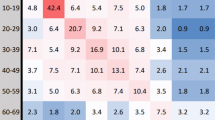
Using the 2006 census data for RC from Statistics Canada10,11, Figure 2a illustrates the clinical attack rate when pre-existing immunity levels are varied in the ranges 0.5 − 0.7 and 0.1 − 0.3 for p1 and p2, respectively. This figure indicates that the attack rate is largely influenced by the pre-existing immunity level of individuals below 50 years of age (p2) and the increase in pre-existing immunity of elderly (p1) has no considerable effect on the incidence of infection. However, with the same total population, as the age profiles (and their employment ratios) shift to resemble those of Winnipeg, the protection of individuals older than 50 years of age becomes more pronounced in reducing the attack rate as p1 increases (Figure 2b).

Figure 2
figure 2

Clinical attack rate with the original household composition of RC as reported in census data with: (a) the original age distribution of RC; (b) a shift to Winnipeg-like age distribution; (c) the original age distribution of RC with switched levels of pre-existing immunity; and (d) a shift to Winnipeg-like age distribution with switched levels of pre-existing immunity.

Full size image

For comparison purposes, we simulated the original and age-shifted scenarios when the levels of pre-existing immunity p1 and p2 are switched. As illustrated in Figure 2c-d, the protection of young adults and children is the main factor in reducing the attack rate, with somewhat more pronounced effects of p1 and p2 when Winnipeg-like age distribution is used (Figure 2d) compared to the original RC age distribution (Figure 2c). All scenarios represented in Figure 2 were simulated without any change in the household composition of RC reported in census data.

Household composition shift

To investigate the effect of shifts in household composition, we first considered the ranges 0.5 − 0.7 and 0.1 − 0.3 for p1 and p2, respectively and simulated the model for a scenario (different from census data) in which the number of persons per household is either 4 or 5, with an average of 4.35. This scenario was considered to evaluate the effect of reduction in the household crowding condition without increasing the number of private dwellings in the community. The distribution procedure for this scenario is described in the Supplementary Information. Figure 3a shows a qualitatively similar pattern as Figure 2a, indicating the importance of increasing p1 in reducing the attack rate. These patterns remain also qualitatively the same when the household composition is shifted to resemble that of Winnipeg (Figure 3b). Since this shift is associated with lower average number of persons per household, the number of dwellings in the community was increased to 795. When the ranges of p1 and p2 are switched (Figures 3c-d), we observed similar effects consistent with simulations in Figures 2c-d, indicating that the protection of individuals below age of 50 remains the key factor for decreasing disease incidence. All scenarios represented in Figures 3 were simulated without any shift in the reported age distribution of RC in census data.

Figure 3
figure 3

Clinical attack rate with the original age profiles of RC as reported in census data and a shift in household size to have: (a) 4 and 5 persons per household; (b) Winnipeg-like composition; (c) 4 and 5 persons per household with switched levels of pre-existing immunity; and (d) Winnipeg-like composition and switched levels of pre-existing immunity.

Full size image

Age and household shifts

We combined shifts in age profile and household composition to simulate the demographic characteristics of Winnipeg with the total population in RC (Figure 4a-b). This combination effectively considers scenarios simulated in Figures 2 and 3 simultaneously. While the protection of young adults and children (p2) remains an important parameter determining the attack rate (Figure 4a), the level of pre-existing immunity in individuals above 50 years of age (p1) has no considerable effect, contrasting the scenario in Figure 2b. Similar results are inferred by switching the ranges of p1 and p2 (Figure 4b), which simultaneously simulates the shifts considered in Figures 2d and 3d.

Figure 4
figure 4

Clinical attack rate for a shift to have: (a) Winnipeg-like age distribution and household composition; (b) Winnipeg-like age distribution and household composition with switched levels of pre-existing immunity.

Full size image

School closures

Using the original demographics of RC we investigated the effect of school closures (upon diagnosis of the first school-aged infectious cases), as a means of transmission reduction. Two scenarios were simulated in which schools were closed for either 4 or 8 weeks and re-opened after each closure period. Compared to the original scenario (Figure 2a), a 4-week school closure has the potential to significantly reduce the attack rate (Figure 5a). When the level of pre-existing immunity is relatively low, the reduction in the overall attack rate is considerably more pronounced for a longer period (e.g., 8-week) of school closure (Figure 5b). We observed similar results with greater reduction in the overall attack rate when the ranges of p1 and p2 are switched (Figures 5c,d). However, due to high levels of pre-existing immunity in the young population, the outcomes of 4-week and 8-week closures are virtually the same, indicating that reactive school closure periods could be shorter when levels of protection (p2) are high in young adults and children.

Figure 5
figure 5

Clinical attack rate with the original demographics of RC as reported in census data for: (a) 4 week school closure; (b) 8 week school closure; (c) 4 week school closure with switched levels of pre-existing immunity; and (d) 8 week school closure with switched levels of pre-existing immunity.

Full size image

Discussion

Using a discrete-time, agent-based simulation model for a remote community in the province of Manitoba, Canada, we have demonstrated that both age profiles and household compositions play an important role in the transmission of influenza within a remote and isolated community. Our findings, in the context of public health, can be summarized as follows:

  • In population settings with crowded living conditions (i.e., many individuals per household), the age distribution of the population can significantly influence the outcome of disease spread and the impact of interventions. If the population is relatively young (with low average age) as observed in many Aboriginal communities10, then protection of young individuals is a primary factor in reducing the overall attack rate (Figure 2a) and protection of the elderly has little impact. This is primarily because even if the proportion of older individuals with pre-existing immunity is high, there are so few individuals in these age groups that it is not sufficient to have any significant effect on reducing disease incidence. However, it is important to note that protection in the elderly remains important for decreasing the risk of developing serious complications as a result of influenza infection, which can lead to costly healthcare interventions (e.g. hospitalization and ICU admission).

  • When the population is relatively young or household sizes are small, the pre-existing immunity in the over-50s age group appears insignificant in reducing the overall attack rate. However, as the average age of the population increases, the protection of older individuals becomes more pronounced in decreasing disease incidence (Figure 2b).

  • In a non-crowded setting where there are a low average number of persons per household, the protection of young people remains an important and dominating factor in reducing disease transmission over time, regardless of the age distribution of the population (Figures 2, 3).

  • When school closure is implemented, significant reductions in the overall attack rate can be achieved and the period of closure can be shortened as the protection of young adults and children increases (Figure 5).

This study has important implications for projecting the potential success of different intervention strategies based on the demographic characteristics of the community (e.g., age distribution and household size). Clearly, what might be optimal interventions for an urban city like Winnipeg may not be as optimal for a remote and isolated community. Our results indicate that target groups for interventions in small population settings with a large number of people per household (crowding) may be different from those in urban centers. An important public health message is that preventing young individuals from infection should not be disregarded due to limited preventive resources or other community factors. However, optimal ways to control infection in young people need to be carefully considered. For instance, school closure might appear to be a useful social distancing measure to employ in small communities in order to prevent transmission between children and reduce the overall attack rate. However, in a setting where households are large and often multigenerational, such a measure may overlook the fact that exposed older family members are at increased risk of suffering serious complications that may require costly healthcare resources, such as hospitalization and intensive care which are not readily available in remote and isolated communities. As discussed in the Supplementary Information, limitations in current health data and contact network data do not lend themselves to analysis of healthcare costs of particular demographic groups. Future work will need to address the variable healthcare costs of particular demographic groups. However, it is clear that understanding the contextual implications of public health measures in communities with low mean age and large household size is of critical importance.

All models make simplifications and rely on assumptions12. We have attempted to develop our model using the best available evidence at this time in order to examine the effect of age and household size on disease transmission. However, there are limitations that are important to consider for future investigation. Interventions such as vaccination have not been explicitly included in the model and this is currently the subject of ongoing research to evaluate the impact of within-community factors on disease intervention strategies. In addition, it is unlikely that public health measures are treated independently. More realistically, multiple intervention strategies are employed that often overlap in time resulting in synergistic effects (e.g. vaccination, antiviral drug therapy and social distancing measures)13. All of these will have significant impacts on epidemic outcomes. In addition, we simplified the model to consider the clinical course of influenza infection; yet we understand that a sizable fraction of infection is transmitted through asymptomatic infection, in which infectious individuals spread the disease without obvious symptoms14. We also assume that some proportion of symptomatic individuals will practice self-isolation; however it is unclear to what extent self-isolation may be adopted by community members as a variety of external factors will likely influence this decision. Furthermore, in the absence of specific data for mobility patterns and time use of individuals in remote and isolated communities, we have structured the model with assumptions consistent with previous work15,16,17.

Our results generated in this study using an agent-based model of a small community in rural Manitoba support the hypothesis that both age structure and household size play an important role in the transmissibility of influenza throughout a remote and isolated community. Identifying novel intervention strategies that address the additional complexities of disease transmission within large households that are often crowded and multigenerational poses a significant challenge for public health professionals. The use of an agent-based model such as the one described here can provide an opportunity to begin to examine optimal intervention strategies for these communities that have specific social and demographic complexities.

Methods

The agent based approach taken here is a discrete-time simulation model15,18, based on the movement of individuals (i.e., agents) that are distributed in a scaled lattice representation of a community (i.e., environment). As described below, a Markov chain compartmental disease state is maintained for each agent in the model. For the inclusion of parameters central to this study, the model was built on compartments representing agents and their epidemiological health status and agent movements and interactions between the compartments in the community. We considered the same 5-year age groupings as provided by the Canadian census data (Figure 1) for determining agent age distribution. Further details of the model and simulator can be found in the Supplementary Information.

Model structure

The underlying structure of the model describes the dynamics of the clinical course of influenza infection and includes health state compartments of susceptible (S), exposed but not yet infectious (E), pre-symptomatic infectious without symptoms (P); infectious with symptoms (I), hospitalized (H) and recovered (R) individuals (Figure 6). We do not explicitly consider asymptomatic infection beyond the pre-symptomatic stage. We further subdivided symptomatic infectious compartment into four classes that are more compatible with observed data: diagnosed (Id ) and undiagnosed (Iu ) compartments that are transient and considered only to generate a count of diagnosed cases and hospitalizations; and the behaviorally distinct compartments of Is (individuals who practice self-isolation and stay home) and Ik (individuals who follow their normal schedule, which also subsume the role of asymptomatic individuals spreading infection). Movements of individuals between these classes occur as a result of a change in epidemiological status or hospitalization of infectious cases over time. Assuming a relatively simple agent schedule for individuals’ mobility, the model captures work, school and household contacts with random mixing for between-agent interactions as detailed in the supplementary Information.

Figure 6
figure 6

Model structure for population compartments for simulation scenarios.

Infectious compartment is divided into four classes of individuals: diagnosed (Id ), undiagnosed (Iu ), self-isolated (Is ) and those who continue with their normal schedule (Ik ).

Full size image

Disease transmission occurs as a result of contact between susceptible and infectious agents. We assumed a standard Markov chain for disease progression in the model compartments. At any time during the epidemic simulation, agents will be in one of these compartments according to their epidemiological status. In our model, each time-step in the simulation is associated with an independent Bernoulli trial for disease transmission. Once exposed, the individual will remain in this compartment for an average duration of TE . After time TE has elapsed, the epidemiological status will change to pre-symptomatic, with an average duration of TP . Following this stage of disease, the infected individual will develop symptoms and will be diagnosed with some probability. A fraction of diagnosed cases will be hospitalized and therefore effectively removed from the simulation scenarios without contributing to infection spread. We assumed that a fraction of infectious individuals who are not hospitalized will self-isolate for an average infectious period TI , sampled from the log-normal distribution19. We also assumed that recovery upon infection will confer immunity against re-infection in the same epidemic episode.

Model parameters

Parameter values used to simulate the model are taken from the estimated ranges published in the literature. The probability of transmission between each susceptible-infectious pair of agents is given by:

where βbase is the baseline transmission rate per unit time (t), pi is the “Age Protection Factor” that models the amount of pre-existing immunity (as a result of prior exposure to an antigenically similar pathogen, for example) in each age group. We assumed two different ranges of pre-existing immunity associated with groups below and above 50 years of age. The effect of this protection was captured by a reduction in transmissibility. The exposed (pre-symptomatic) period was sampled from a uniform distribution with a minimum of 24 (12) and a maximum of 48 (24) hours for TE (PE )19,20. The infectious period TI was sampled from a log-normal distribution with a mean of 74 hours (3.1 days) and standard deviation of 12 hours. Within the published estimates21, we assumed a probability of 0.02 for an infectious case to be diagnosed with laboratory testing following symptoms onset. The age-specific probability of hospitalization was estimated from pandemic data collected for the Burntwood health region in the province of Manitoba, Canada, where the majority of remote and isolated communities are located (see Supplementary Information). The probability of self-isolation was assumed to be 0.8 for children below 18; 0.3 for adults between 19 and 49 years of age; and 0.8 for individuals above age of 5016,17,22.

A key parameter in understanding the nature of an epidemic is the basic reproduction number (R0), defined as the number of secondary cases caused by a single infected case in an entirely susceptible population23. In our model, the level of pre-existing immunity reduces the overall susceptibility of the population and therefore R0 may be higher than the number of secondary cases generated in simulation scenarios. The base transmission probability βbase (in the absence of any pre-existing immunity or limitation to disease spread) was tuned such that the average number of secondary infections over the entire sample of realizations was 1.924.

Population study

The model is based on the demographic characteristics of a remote community (RC) in northern Manitoba with a total population of 1895. The community has no road access to any urban center and air travel is a major conduit. The choice of a remote community for this study was mainly due to recent experience of a disproportionate incidence of infection in that region during the 2009 H1N1 pandemic5. Baseline parameters pertinent to RC demographics, including age and sex profiles and household compositions were obtained from the 2006 census community profiles (catalogue no. 92-591-XWE, 97-554-XCB2006016) of the Statistics Canada databases10,11. Compared to the Winnipeg health region which is the largest urban centre in the province of Manitoba25, remote communities differ significantly in both age distribution and household composition. These demographic variables are illustrated in Figure 1 for occupied private dwellings in RC and Winnipeg.