A universal graph deep learning interatomic potential for the periodic table

Abstract

Interatomic potentials (IAPs), which describe the potential energy surface of atoms, are a fundamental input for atomistic simulations. However, existing IAPs are either fitted to narrow chemistries or too inaccurate for general applications. Here we report a universal IAP for materials based on graph neural networks with three-body interactions (M3GNet). The M3GNet IAP was trained on the massive database of structural relaxations performed by the Materials Project over the past ten years and has broad applications in structural relaxation, dynamic simulations and property prediction of materials across diverse chemical spaces. About 1.8 million materials from a screening of 31 million hypothetical crystal structures were identified to be potentially stable against existing Materials Project crystals based on M3GNet energies. Of the top 2,000 materials with the lowest energies above the convex hull, 1,578 were verified to be stable using density functional theory calculations. These results demonstrate a machine learning-accelerated pathway to the discovery of synthesizable materials with exceptional properties.

Main

Atomistic simulations are the bedrock of in silico materials design. The first step in most computational studies of materials is to obtain an equilibrium structure, which involves navigating the potential energy surface (PES) across all independent lattices and atomic degrees of freedom in search of a minimum. Atomistic simulations are also used to probe the dynamical evolution of materials systems, and to obtain thermodynamic averages and kinetic properties (for example, diffusion constants). Although electronic structure methods such as density functional theory (DFT) provide the most accurate description of the PES, they are computationally expensive and scale poorly with system size.

For large-scale materials studies, efficient, linear-scaling interatomic potentials (IAPs) that describe the PES in terms of many-body interactions between atoms are often necessary. However, most IAPs today are custom-fitted for a very narrow range of chemistries: often for a single element or up to no more than four to five elements. The most popular general purpose IAPs are the AMBER family of force fields^1,2 and the universal force field (UFF)³. However, both were formulated primarily for molecular/organic systems and have limited support and accuracy in modeling crystal structures. More recently, machine learning of the PES has emerged as a particularly promising approach to IAP development^4,5,6,7,8. These so-called ML-IAPs typically express the PES as a function of local environment descriptors such as the interatomic distances and angles, or atomic densities, and have been demonstrated to substantially outperform classical IAPs across a broad range of chemistries⁹. Message-passing and graph deep learning models^10,11,12 have also been shown to yield highly accurate predictions of the energies and/or forces of molecules, as well as a limited number of crystals such as Li₇P₃S₁₁ (ref. ¹³) and Li_xSi_y (ref. ¹⁴) for lithium-ion batteries. Nevertheless, no work has demonstrated a universally applicable IAP across the periodic table and for all crystal types.

In the past decade, the advent of efficient and reliable electronic structure codes¹⁵ with high-throughput automation frameworks^16,17,18,19 has led to the development of large federated databases of computed materials data, including the Materials Project²⁰, AFLOW²¹, Open Quantum Mechanical Database (OQMD)²², NOMAD²³ and so on. Most of the focus has been on making use of the final outputs from the electronic structure computations performed by these databases—namely, the equilibrium structures, energies, band structures and other derivative material properties—for the purposes of materials screening and design. Less attention has been paid to the huge quantities of PES data—that is, intermediate structures and their corresponding energies, forces and stresses—amassed in the process of performing structural relaxations.

In this work we develop the formalism for a graph-based deep learning IAP by combining many-body features of traditional IAPs with those of flexible graph material representations. Using the largely untapped dataset of more than 187,000 energies, 16,000,000 forces and 1,600,000 stresses from structural relaxations performed by the Materials Project since its inception in 2011, we trained a universal IAP for materials based on graph neural networks (GNN) with three-body interactions (M3GNet) for 89 elements of the periodic table with low energy, force and stress errors. We demonstrate the applications of M3GNet in phonon and elasticity calculations, structural relaxations and so on. We further relaxed ~30 million hypothetical structures for new materials discovery.

Results

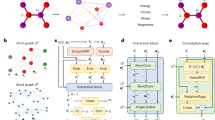
Materials graphs with many-body interactions

Mathematical graphs are a natural representation for crystals and molecules, with nodes and edges representing the atoms and the bonds between them, respectively. Traditional graph neural network models for materials^24,25,26,27 have proven to be exceptionally effective for general materials property predictions^24,25,26,27, but are not suitable as IAPs due to the lack of physical constraints such as a continuity of energies and forces with the changes to the length and number of bonds.

Here we develop a materials graph architecture that explicitly incorporates many-body interactions (Fig. 1). The materials graph is represented as ${{{\mathcal{G}}}}=({{{\mathcal{V}}}},{{{\mathcal{E}}}},{{{\mathcal{X}}}},\left.[{{{\textbf{M}}}},{{{\textbf{u}}}}]\right])$, where ${{{{\textbf{v}}}}}_{i}\in {{{\mathcal{V}}}}$ is atom information for atom i; ${{{{\textbf{e}}}}}_{ij}\in {{{\mathcal{E}}}}$ is the bond information for a bond connecting atoms i and j; and u is the optional global state information. A key difference with past materials graph implementations is the addition of ${{{{\textbf{x}}}}}_{i}\in {{{\mathcal{X}}}}$ (the coordinates for atom i) and M (the optional 3 × 3 lattice matrix in crystals). The graph structure is passed to a graph featurizer that embeds the pair atom distance r_ij—up to a certain cut-off r_c—to basis functions, and the atomic number Z_i to element feature spaces.

Fig. 1: Schematic of the many-body graph potential and the major computational blocks.

The model architecture starts from a position-included graph and then goes through a featurization process, followed by the main block and then the readout module with energy, force and stress outputs. The featurization process consists of the graph featurizer and the many-body computation module. In the graph featurizer, the atomic numbers of elements are embedded into a learnable continuous feature space and the pair bond distances are expanded into a basis set with values and derivatives of up to second order, going to zero at the boundary. The many-body computation module calculates the three- and many-body interaction atom indices and the associated angles. The main block consists of two main steps, namely, the many-body to bond module and the standard graph convolution. The many-body to bond step calculates the new bond information e_ij by considering the full bonding environment ${{{{\mathcal{N}}}}}_{i}$ of atom i via many-body angles such as θ_jik, τ_kijl and so on, and the bond lengths r_ik, r_ij, r_il and so on. The standard graph convolution updates the bond, atom and optional state information iteratively. During the readout stage, the atom information in the graph is passed to a gated multilayer perceptron (MLP) for obtaining the atomic energy, which sums to the total energy. The derivatives of the total energy give force and stress outputs.

The model development takes inspiration from traditional IAPs such as the Tersoff bond-order potential²⁸, where the bond interaction e_ij incorporates n-body interactions using all distinct combinations of n − 2 neighbors in the neighborhood ${{{{\mathcal{N}}}}}_{i}$ of atom i, excluding i and j. We will denote this materials graph with an n-body interactions neural network as MnGNet for brevity. The many-body computations of the graph produce high-order interactions such as angles θ and dihedrals τ and their interactions. The many-body interactions are then aggregated to bonds. Standard graph convolution steps subsequently update the bond, atom and state information. Such many-body calculations and graph convolutions can be repeated N times to construct models of arbitrary complexity, similar to previous materials graph network architectures²⁵. In this work we will focus on incorporation of three-body interactions only (M3GNet).

In the case of IAP fitting, the atom information maps to atom-wise energy E_i and is summed to the total energy E, which is then used to calculate forces f and stresses σ via auto-differentiation.

M3GNet IAP

To develop an IAP using the M3GNet architecture, we used crystal structures with corresponding E, f and σ as targets as training data. The model generates trainable targets via auto-differentiation with f = − ∂E/∂x and σ = V⁻¹∂E/∂ϵ, where x are the atomic coordinates, V is the volume and ϵ is the strain.

Benchmark on IAP datasets

As an initial benchmark, we selected a diverse DFT dataset of elemental energies and forces previously generated by Zuo and co-workers⁹ for face-centered cubic (fcc) nickel, fcc copper, body-centered cubic (bcc) lithium, bcc molybdenum, diamond silicon and diamond germanium. From Table 1, the M3GNet IAPs substantially outperform classical many-body potentials such as the embedded atom method (EAM) and modified EAM (MEAM); they also perform comparably with local environment-based ML-IAPs such as the Behler–Parinello neural network potential (NNP)⁴ and moment tensor potential (MTP)⁷. It should be noted that although ML-IAPs can achieve slightly smaller energy and force errors than M3GNet IAPs, it comes with a substantial loss in flexibility in handling multi-element chemistries because incorporating multiple elements in ML-IAPs usually results in a combinatorial explosion in the number of regression coefficients and the corresponding data requirements. By contrast, the M3GNet architecture represents the elemental information for each atom (node) as a learnable embedding vector. Such a framework is readily extendable to multicomponent chemistries. For instance, the M3GNet-all IAP trained on all six elements performed similarly to the M3GNet IAPs trained on individual elements. The M3GNet framework—like other GNNs—is able to capture long-range interactions without the need to increase the cut-off radius for bond construction (Supplementary Fig. 1). At the same time, unlike the previous GNN models, the M3GNet architecture still maintains a continuous variation of energy, force and stress with changes of the number of bonds (Supplementary Fig. 2), a crucial requirement for IAPs.

Table 1 M3GNet model’s errors compared to the existing models EAM, MEAM, NNP and MTP on the single-element dataset from Zuo and colleagues⁹

Universal IAP for the periodic table

To develop an IAP for the entire periodic table, we leveraged on one of the largest open databases of DFT crystal structure relaxations in the world, that is, the Materials Project²⁰. In total, this dataset, named MPF.2021.2.8, contains 187,687 ionic steps of 62,783 compounds, with 187,687 energies, 16,875,138 force components and 1,689,183 stress components. The dataset covers an energy, force and stress range of [–28.731, 49.575] eV per atom, [–2,570.567, 2,552.991] eV Å⁻¹ and [–5,474.488, 1,397.567] GPa, respectively (Fig. 2a,b). The majority of structures have formation energies between –5 and 3 eV per atom, as shown in Supplementary Fig. 3. Although the distribution of forces is relatively symmetric, the stress data contain a slightly higher proportion of negative (compressive) stresses than positive stresses due to the well-known tendency of the Perdew–Burke–Ernzerhof (PBE) functional to underbind. The radial distribution function g(r) (Fig. 2c) shows that the dataset also spans a broad range of interatomic distances, including small distances of less than 0.6 Å that are essential for the M3GNet model to learn the repulsive interactions at close distances. The dataset encompasses 89 elements of the periodic table with their counts shown in Fig. 2d (see the Methods and Supplementary Table 1 for more information on the MPF.2021.2.8 data).

Fig. 2: The distribution of the MPF.2021.2.8 dataset.

a,b, Structural energy per atom (E) versus distributions of force (a) and stress (b) components. c, The radial distribution function g(r) (dark blue line) and pair atom distance distribution density (light blue histogram). The short distance (<1.1 Å) density is made of mostly hydrogen bonded with oxygen, carbon and nitrogen, as illustrated in the inset. d, Element counts for all atoms in the dataset, covering 89 elements across the periodic table.

Source data

In principle, an IAP can be trained on only energies, or a combination of energies and forces. In practice, the M3GNet IAP trained only on energies (M3GNet-E) was unable to achieve reasonable accuracies for predicting either forces or stresses, with mean absolute errors (MAEs) that are larger than even the mean absolute deviation of the data (Supplementary Table 2). The M3GNet models trained with energies + forces (M3GNet-EF) and energies + forces + stresses (M3GNet-EFS) achieved relatively similar energy and force MAEs, but the MAE in the stresses of the M3GNet-EFS was about half that of the M3GNet-EF model. Accurate stress predictions are necessary for applications that involve lattice changes, for example, structural relaxations or NpT molecular dynamics simulations. Our results suggest that it is critical to include all three properties (energy, force and stress) in model training to obtain a practical IAP. The final M3GNet-EFS IAP (henceforth referred to as the M3GNet model for brevity) achieved an average value of 0.035 eV per atom, 0.072 eV Å⁻¹ and 0.41 GPa for the energy, force and stress test MAE, respectively.

On the test data, the model predictions and the DFT ground truth match well, as revealed by the high linearity and the R² values for the linear fitting between DFT and model predictions (Fig. 3a–c). The cumulative distribution of the model errors indicate that 50% of the data have energy, force and stress errors that are smaller than 0.01 eV per atom, 0.033 eV Å⁻¹ and 0.042 GPa, respectively (Fig. 3d–f). More stringent tests were performed using phonon and elasticity calculations, which were not part of the original training data. The M3GNet model can reproduce accurate phonon dispersion curves and density of states (DOS) of β-cristobalite, stishovite and α-quartz SiO₂ (Supplementary Fig. 4) to quantitative agreements with expensive DFT computations²⁹. The M3GNet phonon DOS centers ($\bar{\omega }$) from phonon calculations using predicted forces and the frozen phonon approach are also in good agreement with density functional perturbation theory-computed values with a MAE of 44.2 cm⁻¹ (Fig. 3g)²⁹. The systematic underestimation by the M3GNet model relative to DFT is probably due to the different choices of pseudopotentials; the DFT phonon calculations were performed using the PBEsol³⁰ functional whereas the M3GNet training data comprised PBE/PBE + U calculations^31,32. This systematic underestimation can be corrected with a constant shift of 31.6 cm⁻¹ and the MAE reduces to 28.8 cm⁻¹. Such errors are even smaller than a state-of-the-art phonon DOS peak position prediction model which reported MAE of 36.9 cm⁻¹ (ref. ³³). We note that the DOS peak prediction model does not exhibit a systematic shift as it was directly fitted on the data by minimizing a mean squared error. Similar to DFT, the relationship $\bar{\omega }\propto 1/{(\overline{m})}^{2}$ (where $\bar{\omega }$ is the average frequency and $\overline{m}$ is the average atomic mass) is obtained (Supplementary Fig. 5). The M3GNet-calculated Debye temperatures are less accurate (Fig. 3h), which can be attributed to relatively poor M3GNet predictions of the shear moduli (R² = 0.134; Supplementary Fig. 6); the bulk moduli predictions (R² = 0.757), however, are reasonable.

Fig. 3: The model predictions on the test dataset compared to DFT calculations.

a–c, The parity plots for the energy (a), force (b) and stress (c). The model predicted results are $\hat{E}$, $\hat{f}$ and $\hat{\sigma }$. The dashed lines (y = x) are guides for the eye. d–f, The cumulative distribution of errors for the energy (d), force (e) and stress (f). The horizontal dashed lines indicate the model errors at 50%, 80% and 95% (from the bottom to the top, respectively). g, Comparisons between the model-calculated 1,521 phonon DOS centers data ($\hat{\omega }$) and the PBEsol DFT calculations ($\bar{\omega }$) by Petretto and co-workers²⁹. h, Comparisons between the 11,848 Debye temperatures (excluding negative moduli) calculated from the M3GNet model (${\hat{T}}_{{{{\rm{Debye}}}}}$) and the PBE DFT elastic tensors from de Jong et al.⁶⁴.

Source data

The M3GNet IAP was then applied in a simulated materials discovery workflow where the final DFT structures are not known a priori. M3GNet relaxations were performed on the initial structures from the test dataset of 3,140 materials. M3GNet relaxation yields crystals with volumes that are much closer to the DFT reference volumes (Fig. 4a). Although 50% and 5% of the initial input structures have volumes that differ from the final DFT-relaxed crystals by more than 2.4% and 22.2%, respectively, these errors are reduced to 0.6% and 6.6%, respectively, via M3GNet relaxation. Correspondingly, the errors in the predicted energies $\hat{E}$ are also much smaller (Fig. 4b). Using the initial structures for direct model predictions, the energy differences distribute broadly, with a considerable number of structures having errors that are larger than 0.1 eV per atom. All errors here were calculated relative to the DFT energies of the final DFT-relaxed structures for each material. The overall MAE is 0.169 eV per atom with ~20% of the structures having errors that are larger than 0.071 eV per atom (Fig. 4b). These errors are far too large for reliable estimations of materials stability, given that about 90% of all inorganic crystals in the Inorganic Crystal Structure Database (ICSD) have an energy above the convex hull smaller than 0.067 eV per atom (ref. ³⁴). By contrast, energy calculations on the M3GNet-relaxed structures yield an MAE of 0.035 eV per atom, and 80% of the materials have errors smaller than 0.028 eV per atom. The error distributions using M3GNet-relaxed structures are close to the case in which we know the DFT final structures (Fig. 4b) which suggests that the M3GNet potential can be accurate in helping obtain the correct structures. In general, relaxations with M3GNet converge rapidly, as shown in Supplementary Fig. 7. An example of M3GNet relaxation is shown in Supplementary Fig. 8 for K₅₇Se₃₄ (Materials Project ID mp-685089), a material with one of the largest energy changes during relaxation. Convergence is achieved after about 100 steps when the forces fall below 0.1 eV Å⁻¹. The X-ray diffraction pattern of the M3GNet-relaxed structure also resembles the counterpart from DFT relaxation (Supplementary Fig. 8g). This relaxation can be performed on a laptop in about 22 s on a single Intel(R) Xeon(R) CPU E5-2620 v.4 2.10 GHz core, whereas the corresponding DFT relaxation took 15 h on 32 cores in the original Materials Project calculations.

Fig. 4: Relaxation of crystal structures with M3GNet.

a, Distribution of the absolute percentage error in volumes of M3GNet-relaxed structures relative to DFT-relaxed structures. b, The differences between M3GNet-predicted energies ($\hat{E}$) and ground-state energies (E_gs) using the initial M3GNet- and DFT-relaxed structures; E_gs is defined as the DFT energy of the DFT-relaxed crystal. The horizontal dashed lines mark the 50th, 80th and 95th percentiles of the distributions (from the bottom to the top, respectively), and the corresponding x-axis values are annotated.

Source data

New materials discovery

The ability of M3GNet to accurately and rapidly relax arbitrary crystal structures, and predict their energies, makes it ideal for large-scale materials discovery. We generated 31,664,858 candidate structures as starting points (see Methods for details), used M3GNet IAP to relax the structures and calculated the signed energy distance to the Materials Project convex hull (E_hull-m); 1,849,096 materials have a E_hull-m of less than 0.01 eV per atom.

A formation energy model based on the Matbench³³ Materials Project data was developed using the same architecture as the M3GNet IAP model (see Supplementary Table 3). Materials with a difference in the signed energy distance to the Materials Project convex hull from this model (E_hull-f) and a E_hull-m of greater than 0.2 eV per atom were discarded in the subsequent DFT analysis. This extra step removes materials with higher energy prediction uncertainties, which account for 13.2% (243,820) of the predicted materials. It should be noted that this step can also be omitted to simplify the discovery workflow, although potentially with an impact on the hit rate of stable materials discovery. The top-1,000 lowest E_hull-m materials from any chemistry, and the top-1,000 metal oxides with elements from the first five rows (excluding technetium due to radioactivity and rubidium due to high dominance), were then selected for validation via DFT relaxation and energy calculations. Only the most stable polymorphs were selected for each composition. It was found that the distribution in the DFT-calculated E_hull−dft matches well with the distributions of E_hull-m (Fig. 5a). For most computational materials discovery efforts, a positive threshold—typically around 0.05–0.1 eV per atom—is applied to identify synthesizable materials. This positive threshold accounts for both errors in DFT-calculated energies and the fact that some thermodynamically meta-stable materials can be realized experimentally. Of the top-1,000 materials from any chemistry, 999 were found to have a E_hull−dft of less than 0.001 eV per atom (Fig. 5b), and none of them were in the Materials Project database. For the top-1,000 oxides, 579, 826 and 935 were found to be synthesizable on the basis of E_hull−dft thresholds of 0.001, 0.05 and 0.1 eV per atom, respectively (Fig. 5b). Out of the 579 DFT-stable oxides, only five (namely, Mg₄Nb₂O₉, Sr₃V₂O₈, K₂SnO₂, Cd(RhO₂)₂ and CoMnO₄) were previously known and matched with the Materials Project structures. The effectiveness of the M3GNet IAP relaxations can be seen in Supplementary Fig. 9, which shows that the energy changes during subsequent DFT relaxations (of the MEG3Net-relaxed structures) are at least one order of magnitude smaller than the energy changes during M3GNet relaxation. The final M3GNet-relaxed energies are in excellent agreement with the final DFT-relaxed energies, with MAEs of 0.112 and 0.045 eV per atom for the top-1,000 materials in the any-chemistry and oxide-chemistry categories, respectively (Fig. 5c,d). Using the M3GNet IAP, we have also assessed the dynamic stability of the 1,578 materials with a E_hull−dft of less than 0.001 eV per atom using phonon calculations. A total of 328 materials do not exhibit imaginary frequencies in their M3GNet phonon dispersion curves. Four phonon dispersion curves are shown in Extended Data Fig. 1; the others are provided in ‘Data availability’ section.

Fig. 5: Discovery of stable materials using M3GNet.

a, The signed E_hull distribution for the top-1,000 lowest E_hull-m materials from any chemistry and oxides only. b, Fraction of materials below E_hull−dft among top-1,000 materials in the all and oxides categories. c,d, Plot of the final M3GNet-predicted energy against final DFT energy for the all (c) and oxides (d) categories.

Source data

As a further evaluation of the performance of M3GNet for materials discovery, we computed the discovery rate, that is, the fraction of DFT-stable materials (E_hull−dft ≤ 0) for 1,000 structures uniformly sampled from the ~1.8 million materials with a E_hull-m of less than 0.001 eV per atom. The discovery rate remains close to 1.0 up to a E_hull-m threshold of around 0.5 eV per atom, and remains at a reasonably high value of 0.31 at the strictest threshold of 0.001 eV per atom, as shown in Supplementary Fig. 10. For this material set, we also compared the DFT relaxation time cost with and without M3GNet pre-relaxation. The results show that without M3GNet pre-relaxation, the DFT relaxation time cost is about three times of that with the M3GNet relaxation, as shown in Supplementary Fig. 11.

Discussion

A universal IAP such as M3GNet has applications beyond crystal structure relaxation and stability predictions. For instance, a common application of IAPs is in molecular dynamics simulations to obtain transport properties such as diffusivity and ionic conductivity. An example of a M3GNet application is in Supplementary Fig. 12 for Li₃YCl₆. Training an IAP for complex multicomponent systems such as Li₃YCl₆ is typically a highly involved process³⁵, whereas the M3GNet IAP can be universally applied to any material without further retraining. For example, M3GNet molecular dynamics calculations could be applied to a wide range of lithium-containing compounds to identify potential lithium superionic conductors (Supplementary Fig. 13). Furthermore, the M3GNet IAP could also serve as a surrogate model in lieu of DFT with other structural exploration techniques (for example, evolutionary algorithms such as USPEX³⁶ and CALYPSO³⁷, or generative models such as CDVAE³⁸) to generate more diverse and unconstrained candidates.

It should be noted that the current M3GNet IAP reported in this work is the best that can be obtained at present with the available data. Further improvements in accuracy can be achieved through several efforts. First, the training data for the M3GNet IAP come from DFT-relaxation calculations in the Materials Project, which were performed with less stringent convergence criteria such as a lower energy cut-off and sparser k-point grids. For IAP development, the best practice is to obtain accurate energies, forces and stresses via single-point, well-converged DFT calculations for training data. Building such a database is an extensive effort that is planned for future developments in the Materials Project. Second, active learning strategies (for instance, by using the DFT relaxation data from the M3GNet-predicted stable crystals in a feedback loop) can be used to systematically improve the M3GNet IAP, especially in underexplored chemical spaces with the greatest potential for materials discoveries. Nevertheless, about 1.8 million of the 31 million candidates were predicted to be potentially stable or meta-stable by M3GNet against materials in the Materials Project, which already expands the potential exploration pool by an order of magnitude over the ~140,000 crystals in the Materials Project database today. We shall note that the potentially stable materials will need to be further verified with DFT calculations and experimental syntheses. The model uncertainty will also play a role in further decreasing the number of true discoveries. Systematic methods for quantifying uncertainty are likely to further increase model fidelity.

Finally, the M3GNet framework is not limited to crystalline IAPs or even IAPs in general. The M3GNet formalism without lattice inputs and stress outputs is naturally suited for molecular force fields. When benchmarked on MD17 and MD17-CCSD(T) molecular force-field data (Supplementary Tables 4 and 5)^39,40,41, the M3GNet models were found to be more accurate than the embedded atom neural network force field⁴², and to perform comparably with the state-of-the-art message-passing networks and equivariant neural network models. Moreover, by changing the readout section from summed atomic energy as in Fig. 1 to intensive property readout, the M3GNet framework can be used to develop surrogate models for property prediction. We trained M3GNet models on the Matbench materials data covering nine general crystal materials properties (Supplementary Table 3)³³. In all cases, the M3GNet models achieved excellent accuracies.

Methods

Data source

The Materials Project performs a sequence of two relaxation calculations¹⁹ with the PBE⁴³ generalized gradient approximation (GGA) functional or the GGA + U method⁴⁴ for every unique input crystal, typically obtained from an experimental database such as the Inorganic Crystal Structure Database⁴⁵. Our initial dataset comprises a sampling of the energies, forces and stresses from the first and middle ionic steps of the first relaxation and the last step of the second relaxation for calculations in the Materials Project database that contains GGA Structure Optimization or GGA + U Structure Optimization task types as of 8 February 2021. The snapshots that have a final energy per atom greater than 50 eV per atom or atom distance less than 0.5 Å were excluded as those tend to be the result of errors in the initial input structure.

This dataset is then split into the training, validation and test data in the ratio of 90%, 5% and 5%, respectively, according to materials not data points. Three independent data splits were performed.

Materials discovery methods

To generate initial materials candidates, combinatorial isovalent ionic substitutions based on the common oxidation states of non-noble-gas element were performed on 5,283 binary, ternary and quaternary structural prototypes in the 2019 version of the ICSD⁴⁵ database. Only prototypes with less than 51 atoms were selected for computational speed considerations. Further filtering was performed to exclude structures with non-integer or zero-charged atoms. A total of 31,664,858 hypothetical materials candidates were generated, more than 200 times the total number of unique crystals in the Materials Project today. The candidate space contains 294,643 chemical systems, whereas the Materials Project has only about 47,000 chemical systems. This represents a quantity and chemical diversity of materials that is inaccessible using current DFT or other IAP implementations.

All structures were relaxed using the M3GNet model and their signed energy distance to the Materials Project convex hull were calculated using the M3GNet IAP-predicted energy (E_hull-m). We acknowledge that some of the generated structures may compete with each other for stability; however, to avoid introducing additional uncertainties into the E_hull-m predictions, we have elected to compute E_hull-m relative to ground-truth DFT energies in the Materials Project as opposed to the higher uncertainty M3GNet-computed energies. A zero or negative E_hull means that the material is predicted to be potentially stable compared to known materials in MP. In total, 1,849,096 materials have E_hull-m less than 0.001 eV per atom. We then excluded materials that have non-metal ions in multiple valence states, for example, materials containing Br⁺ and Br⁻ at the same time and so on. It is well-known that PBE overbinds single-element molecules such as O₂, S₈, Cl₂ and so on, and negative anion energy corrections are applied to ionic compounds in Materials Project to offset such errors.⁴⁶ However the corrections are based mostly on composition, which may artificially overstabilize materials with multivalence non-metal ions. We have developed a searchable database for the generated hypothetical structures and their corresponding M3GNet-predicted properties at http://matterverse.ai.

Model construction

Neural network definition

If we denote one layer of the perceptron model as

$${{{{\mathcal{L}}}}}_{g}^{k}:x\mapsto g({{{{\textbf{W}}}}}_{k}x+{{{{\textbf{b}}}}}_{k})$$

(1)

then the K-layer MLP can be expressed as

$${\xi }_{K}(x)=({{{{\mathcal{L}}}}}_{g}^{K}\circ {{{{\mathcal{L}}}}}_{g}^{K-1}\circ ...{{{{\mathcal{L}}}}}_{g}^{1})(x)$$

(2)

The K-layer gated MLP becomes

$${\phi }_{K}(x)=(({{{{\mathcal{L}}}}}_{g}^{K}\circ {{{{\mathcal{L}}}}}_{g}^{K-1}\circ ...{{{{\mathcal{L}}}}}_{g}^{1})(x))\odot (({{{{\mathcal{L}}}}}_{\sigma }^{K}\circ {{{{\mathcal{L}}}}}_{g}^{K-1}\circ ...{{{{\mathcal{L}}}}}_{g}^{1})(x))$$

(3)

where ${{{{\mathcal{L}}}}}_{\sigma }^{K}(x)$ replaces the activation function g(x) of ${{{{\mathcal{L}}}}}_{g}^{K}(x)$ to sigmoid function σ(x), and ⊙ denotes the element-wise product. The gated MLP comprises the normal MLP before ⊙ and the gate network after ⊙.

Model architecture

The neighborhood of atom i is denoted as ${{{{\mathcal{N}}}}}_{i}$. We consider all other bonds emanating from atom i when calculating the bond interaction of e_ij. To incorporate n-body interactions, each e_ij is updated using all distinct combinations of n − 2 neighbors in ${{{{\mathcal{N}}}}}_{i}$ excluding atom j (that is, ${{{{\mathcal{N}}}}}_{i}/j$), denoted generally as follows:

$${\tilde{{{{\boldsymbol{e}}}}}}_{ij}=\mathop{\sum}\limits_{\genfrac{}{}{0ex}{}{{k}_{1},{k}_{2},...,{k}_{n-2}\in {{{{\mathcal{N}}}}}_{i}/j}{{k}_{1}!={k}_{2}!=...{k}_{n-2}}}{\phi }_{n}({{{{\boldsymbol{e}}}}}_{ij},{{{{\boldsymbol{r}}}}}_{ij},{{{{\boldsymbol{v}}}}}_{j},{{{{\boldsymbol{r}}}}}_{i{k}_{1}},{{{{\boldsymbol{r}}}}}_{i{k}_{2}},...,{{{{\boldsymbol{r}}}}}_{i{k}_{n-2}},{{{{\boldsymbol{v}}}}}_{{k}_{1}},{{{{\boldsymbol{v}}}}}_{{k}_{2}},...,{{{{\boldsymbol{v}}}}}_{{k}_{n-2}})$$

(4)

where ϕ_n is the update function and r_ik is the vector pointing from atoms i to k. In practice, this n-body information exchange involves the calculation of distances, angles, dihedral angles, improper angles and so on, which escalates combinatorially with the order n as (M_i − 1)!/(M_i − n + 1)!, where M_i is the number of neighbors in ${{{{\mathcal{N}}}}}_{i}$. We will denote this materials graph with an n-body interactions neural network as MnGNet. In this work, we will focus on the incorporation of three-body interactions only (M3GNet).

Let θ_jik denote the angle between bonds e_ij and e_ik. Here we expand the three-body angular interactions using an efficient complete and orthogonal spherical Bessel function and spherical harmonics basis set, as proposed by Klicpera and colleagues¹¹. The bond update equation can then be rewritten as:

$${\tilde{{{{\textbf{e}}}}}}_{ij}=\mathop{\sum}\limits_{k}{j}_{l}({z}_{{ln}}\frac{{r}_{ik}}{{r}_{\mathrm{c}}}){Y}_{l}^{0}({\theta }_{jik})\odot \sigma ({{{{\textbf{W}}}}}_{v}{{{{\textbf{v}}}}}_{k}+{{{{\textbf{b}}}}}_{v}){f}_{\mathrm{c}}({r}_{ij}){f}_{\mathrm{c}}({r}_{ik})$$

(5)

$${{{{\textbf{e}}}}}_{ij}^{\prime}={{{{\textbf{e}}}}}_{ij}+g(\tilde{{{{{\textbf{W}}}}}_{2}}{\tilde{{{{\textbf{e}}}}}}_{ij}+{\tilde{{{{\textbf{b}}}}}}_{2})\odot \sigma (\tilde{{{{{\textbf{W}}}}}_{1}}{\tilde{{{{\textbf{e}}}}}}_{ij}+{\tilde{{{{\textbf{b}}}}}}_{1})$$

(6)

where W and b are learnable weights from the network; j_l is the spherical Bessel function with the roots at z_ln, i.e., j_l(z_ln) = 0; ${Y}_{l}^{0}$ is the spherical harmonics function; σ is the sigmoid activation function; ${f}_{\mathrm{c}}(r)=1-6{(r/{r}_{\mathrm{c}})}^{5}+15{(r/{r}_{\mathrm{c}})}^{4}-10{(r/{r}_{\mathrm{c}})}^{3}$ is the cut-off function ensuring that the functions vanished smoothly at the neighbor boundary⁴⁷; g(x) = xσ(x) is the nonlinear activation function⁴⁸; and ${\tilde{{{{\textbf{e}}}}}}_{ij}$ is a vector of length n_maxl_max, expanded by indices l = 0, 1, ... , l_max − 1 and n = 0, 1, ... , n_max − 1.

Following the n-body interaction update, several graph convolution steps are carried out sequentially to update the bond, atom and—optionally—the state information, as follows:

$${{{{\textbf{e}}}}}_{ij}^{\prime}={{{{\textbf{e}}}}}_{ij}+{\phi }_{e}({{{{\textbf{v}}}}}_{i}\oplus {{{{\textbf{v}}}}}_{j}\oplus {{{{\textbf{e}}}}}_{ij}\oplus {{{\textbf{u}}}}){{{{\textbf{W}}}}}_{e}^{0}{{{{\textbf{e}}}}}_{ij}^{0}$$

(7)

$${{{{\textbf{v}}}}}_{i}^{\prime}={{{{\textbf{v}}}}}_{i}+\mathop{\sum}\limits_{j}{\phi }_{e}^{\prime}({{{{\textbf{v}}}}}_{i}\oplus {{{{\textbf{v}}}}}_{j}\oplus {{{{\textbf{e}}}}}_{ij}^{\prime}\oplus {{{\textbf{u}}}}){{{{\textbf{W}}}}}_{e}^{0^{\prime} }{{{{\textbf{e}}}}}_{ij}^{0}$$

(8)

$${{{{\textbf{u}}}}}^{\prime}=g({{{{\textbf{W}}}}}_{2}^{u}g({{{{\textbf{W}}}}}_{1}^{u}(\frac{1}{{N}_{v}}\mathop{\sum }\limits_{i}^{{N}_{v}}{{{{\textbf{v}}}}}_{i}\oplus {{{\textbf{u}}}})+{{{{\textbf{b}}}}}_{1}^{u})+{{{{\textbf{b}}}}}_{2}^{u})$$

(9)

where ϕ_e(x) and ${\phi }_{e}^{\prime}(x)$ are gated MLPs, as in equation (3); ⊕ is the concatenation operator; N_v is the number of atoms; and ${{{{\boldsymbol{e}}}}}_{ij}^{0}$ represents the distance-expanded basis functions with the target values, and the first and second derivatives smoothly going towards zero at the cut-off boundary (see Methods). Such a design ensures that the target values and their derivatives up to second order change smoothly with changes in the number of bonds; u inputs and updates are optional to the models as not all structures or models have state attributes.

Materials graphs were constructed using a radial cut-off of 5 Å. For computational efficiency considerations, the three-body interactions were limited to within a cut-off of 4 Å. The graph featurizer converts the atomic number into embeddings of dimension 64. The bond distances were expanded using the continuous and smooth basis function proposed by Kocer et al.⁴⁹, which ensures that the first and second derivatives vanish at the cut-off radius.

$${h}_{m}(r)=\frac{1}{\sqrt{{d}_{m}}}\left[{f}_{m}(r)+\sqrt{\frac{{e}_{m}}{{d}_{m-1}}}{h}_{m-1}(r)\right]$$

(10)

where

$${d}_{m}=1-\frac{{e}_{m}}{{d}_{m-1}}$$

(11)

$${e}_{m}=\frac{{m}^{2}{(m+2)}^{2}}{4{(m+1)}^{4}+1}$$

(12)

$$\begin{array}{l}{f}_{m}(r)={(-1)}^{m}\frac{\sqrt{2}\uppi }{{r}_{c}^{3/2}}\frac{(m+1)(m+2)}{\sqrt{{(m+1)}^{2}+{(m+2)}^{2}}}\\\left({\mathrm{sin c}}\left(r\frac{(m+1)\uppi }{{r}_{c}}\right)+{\mathrm{sin c}}\left(r\frac{(m+2)\uppi }{{r}_{c}}\right)\right)\end{array}$$

(13)

$${\mathrm{sin c}}(x)=\frac{\sin x}{x}$$

(14)

${{{{\textbf{e}}}}}_{ij}^{0}$ is a vector formed by m basis functions of h(r).

$${{{{\textbf{e}}}}}_{ij}^{0}({r}_{ij})=[{h}_{1}({r}_{ij}),{h}_{2}({r}_{ij}),...,{h}_{m}({r}_{ij})]$$

(15)

In this work, we used three basis functions for the pair distance expansion.

The main blocks consist of three three-body information exchange and graph convolutions (N = 3 in Fig. 1). By default, the values of W and b in equations (5–9) give output dimensions of 64. Each gated MLP (ϕ_e(x) and ${\phi }_{e}^{\prime}(x)$ in equations (7) and (8)) have two layers with 64 neurons in each layer.

For the prediction of extensive properties such as total energies, a three-layer gated MLP (equation (3)) was used on the atom attributes after the graph convolution and sum the outputs as the final prediction, that is,

$${p}_{{{{\rm{ext}}}}}=\mathop{\sum}\limits_{i}{\phi }_{3}({{{{\boldsymbol{v}}}}}_{i})$$

(16)

The gated MLP ϕ₃(x) operating on node attributes v_i has a layer neuron configuration of [64, 64, 1] and no activation in the last layer of the normal MLP part.

For the prediction of intensive properties, the readout step was performed as follows by including optional state information u after the main blocks.

$${p}_{{{{\rm{int}}}}}={\xi }_{3}(\mathop{\sum}\limits_{i}{w}_{i}{\xi }_{2}({{{{\textbf{v}}}}}_{i})\oplus {{{\textbf{u}}}})$$

(17)

with weights w_i summing to 1 and defined as

$${w}_{i}=\frac{{\xi }_{3}^{\prime}({{{{\textbf{v}}}}}_{i})}{\mathop{\sum}\limits_{i}{\xi }_{3}^{\prime}({{{{\textbf{v}}}}}_{i})}$$

(18)

ξ₃ and ${\xi }_{3}^{\prime}$ have neuron configurations of [64, 64, 1] to ensure the output is scalar. There is no activation in the final layer of the MLP for regression targets, whereas, for classification targets, the last layer activation is chosen as the sigmoid function.

In the training of MPF.2021.2.8 data, the M3GNet model comprises three main blocks with 227,549 learnable weights.

Model training

The Adam optimizer⁵⁰ was used with an initial learning rate of 0.001, with a cosine decay to 1% of the original value in 100 epochs. During optimization, the validation metric values were used to monitor the model convergence, and training was stopped if the validation metric did not improve for 200 epochs. For the elemental IAP training, the loss function was the mean squared error. For other properties, we used the Huber loss function⁵¹ with δ set to 0.01. For universal IAP training, the total loss function includes the loss for energy, forces and—in inorganic compounds—the stresses. A batch size of 32 was used in model training.

$$L=\ell (e,{e}_{\mathrm{DFT}})+{w}_{f}\ell ({{{\textbf{f}}}},{{{\textbf{f}}_{\mathrm{DFT}}}})+{w}_{\sigma }\ell ({{{{\upsigma }}}},{{{{{\upsigma }}}_{\mathrm{DFT}}}})$$

(19)

where ℓ is the Huber loss function, e is energy per atom and w are the scalar weights. The DFT subscripts indicate data from DFT.

Before M3GNet IAP fitting, we fit the elemental reference energies using linear regression of the total energies. We first featurize a composition into a vector c = [c₁, c₂, c₃, ... , c₈₉] where c_i is the number of atoms in the composition with the atomic number i. The composition feature vector c is mapped to the total energy of the material E via E = ∑_ic_iE_i, where E_i is the reference energy for an element with atomic number i that can be obtained by linear regression of the training data. The elemental reference energies were then subtracted from the total energies to improve M3GNet model training stability. We set w_f = 1 and w_σ = 0.1 during training the MPF.2021.2.8 data.

Software implementation

The M3GNet framework was implemented using the TensorFlow⁵² package and currently runs on TensorFlow v.2.9.1. All crystal and molecular structure processing were performed using the Python Materials Genomics (pymatgen)¹⁶ v.2020.12.31. The structural optimization was performed using the FIRE⁵³ algorithm implemented in the atomic simulation environment (ASE) v.3.22.0 (ref. ⁵⁴). The molecular dynamics simulations were performed in the NVT ensemble using ASE (ref. ⁵⁴). Phonon calculations were performed using the Phonopy package v.2.10.0 (ref. ⁵⁵). Data analysis and visualization were performed using scikit-learn v.0.24.2 (ref. ⁵⁶), statsmodels v.0.12.2 (ref. ⁵⁷), matplotlib v.3.3.0 (ref. ⁵⁸), seaborn v.0.11.2 (ref. ⁵⁹) and pandas v.1.3.1 (ref. ⁶⁰).