Introduction

Extreme sea levels intensely impact infrastructure and socio-environmental systems in the coastal regions, including pronounced property and environmental damage and loss of life. Although ordinary people are often focused on the chronic effects of the mean sea level rise, the major devastating threats (e.g., flooding and erosion) to the coastal regions originated from episodes of extreme storm surges. In the United States, 40% of the population lives in low-lying coastal areas, and ~48% of the national Gross Domestic Product (GDP) is generated from the coastal counties1. Therefore, extreme sea levels are critical for the coastal regions because they can cause costly disaster events in the U.S.2 and many other regions worldwide3. Hurricane Katrina in New Orleans displaced more than a million people and caused economic damage of about $100 billion. Likewise, Hurricane Sandy struck the New York region in 2012 and caused $50 billion in economic losses. Besides, climate model projections indicate notable increases in the frequency and magnitude of extreme sea levels, along with future increases in income, may cause more devastating situations and economic losses in the future4,5,6,7,8. Coastal planners quantify the risks of extreme sea levels by estimating the exceeding probability of a certain extreme event (i.e., return period), to design and plan the coastal protection measures. Extreme value analysis is employed for risk computation, which usually requires longer data records. An ongoing challenge in coastal flood risk assessment and risk reduction exercise is the limited sea level data in space and time. Long records of sea level data from tide gauges (TGs) are sparse, and many coastal areas lack in situ information.

In coastal flood risk assessment, extreme value theory provides the most useful statistical framework for estimating the exceedance probability of extreme events9,10,11. The most used approach in analyzing extreme sea levels is the site-by-site analysis, where typically generalized extreme value (GEV) or Generalized Pareto (GP) distribution is fitted to extreme sea levels defined by either block-maxima (considered the maximum value within a time window, i.e., year) or peak-over threshold (consider all values above a certain threshold) method, respectively11. Numerous studies investigated storm surge extremes at global and regional scales employing the site-by-site approach by fitting extreme value models to extreme sea levels identified by block maxima or peak-over-threshold method7,12,13,14,15,16,17,18,19,20,21. The site-by-site analysis is sensitive to record length and outliers, leading to higher uncertainty bands, and estimates at ungauged locations are not apparent. To eliminate the limitations, several studies proposed pooling storm surge information from the nearby tide gauges over a region with similar storm surge statistical characteristics (i.e., Regional Frequency Analysis, RFA)22,23,24. The RFA method identifies homogeneous areas and fits an extreme value distribution to extreme data pooled from the homogeneous area. Though the approach may provide a more accurate estimation of event probabilities, identifying homogeneous areas may be challenging and it can lead to discontinuous and unsmooth spatial extreme fields having artificial boundaries without reasonable physical explanations. Besides, RFA does not account for inter-site dependence in the regional pooling, which may lead to incorrect event probabilities and artificially reduce uncertainty though a methodological modification has recently been proposed to address this issue25. An alternative to the RFA is to model extremes employing a spatial Bayesian hierarchical model where latent Gaussian processes are specified on the distributional parameters to pool spatial information. However, this approach assumes that the data at different sites are conditionally independent, and the spatial dependence included in the model only through the latent processes.

The max-stable process can overcome these limitations by incorporating a max-stable dependence structure to produce a more realistic spatial surface of extremes than the standard latent variable framework. It allows sharing information across sites, estimating GEV parameters at ungauged locations, and reducing uncertainty26. The max-stable process can be regarded as the spatial variant of univariate GEV distribution (i.e., spatial GEV); however, the earlier one differs from the typical “spatial GEV”, in which univariate GEV parameters are modeled as a function of spatial locations and possibly other covariates. The spatial GEV spatially interpolates GEV parameters, assuming spatial independence between neighboring stations, which may lead to unrealistic spatial inference and prediction27,28. Despite its fidelity in modeling spatial extremes, the max-stable process (i.e., asymptotic model) may be limited to adequately capture the more localized extreme events due to rigid dependence structures29. The max-stable process is always asymptotically dependent unless they are fully independent, which indicates that the strength of spatial dependence does not vanish as events become more extreme. Fitting the max-stable process to data requires a pairwise likelihood function instead of the typical likelihood function. While pairwise likelihood approach generally provides valid inference, it might be less efficient than the likelihood approach due to loss of information30.

The application of the max-stable process in analyzing storm surge extremes has not been adequately explored, though it has been widely applied for analyzing other hydrologic extremes (e.g., rainfall)31,32. Calafat and Marta33 employ max-stable process models under a Bayesian hierarchical framework to develop a probabilistic reanalysis of storm surge extremes for the European coasts. In contrast to the statistical methods, hydrodynamic models have been employed to generate global reanalysis of storm surges and extreme sea levels34,35 and explicitly modified and tested for the US east and Gulf of Mexico (GOM) coasts36. Hydrodynamic models require extensive computation, while statistical models can provide comparable performance in generating extreme surge probabilities and their spatial fields at a significantly lower cost33,37.

Despite the limitations of accurate and reliable estimates of storm surge extreme probabilities at a gauged or ungauged location because of sparse records in space and time, very few researchers have explicitly derive the spatial fields of the probabilities of storm surge extremes. Besides, almost no studies simulate storm surge extremes stochastically by exploiting dependence and sharing the extreme surge information across TGs for the US coasts. In this research, we develop models employing the max-stable process to compute GEV distribution parameters at grid locations along the contiguous United States (CONUS) coastlines using the annual maximum (AM) surges from 1950 to 2017 at 41 long-record TGs. We then stochastically generate synthetic AM surge time series and incorporate the spatial-temporal variability using rank ordering (i.e., reorder them to match the observed ranks).

Results

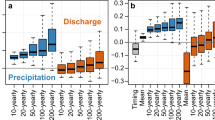
Max-stable model is fitted to the AM surges to compute the GEV distribution parameters at each TG following the leave-one-out validation approach. We evaluate the model efficiency by estimating the relative differences of the computed GEV parameters (1) compared to those estimated by the max-stable model using AM surges from all the 41 TGs instead of leave-one-out and (2) compared to the GEV parameters estimated by fitting univariate GEV distribution to AM surges at each TG, separately. The former one shows little/no difference, indicating that the max-stable model is highly efficient. For the latter one (compared to the at-site GEV parameters), the relative differences for the location and scale parameters vary from 0.001 to 0.8 and 0.02 to 3.4, respectively (Fig. 1). The medians of RD (across all TGs) of the location and scale parameters are 0.15 and 0.32, respectively, suggesting the errors, on average, within ~15% and 32% of the observations. The average errors in the computed GEV parameters are mainly influenced by the errors at the Key West TG, which are significantly higher than the other TGs. The reason behind this behavior is not apparent, however, being located at a relatively long distance from the nearby TGs and having significantly lower variability in the AM surges (variance at Key West is 80% and 54% lower than the nearby selected TGs Fernandina Beach and St. Petersburg, respectively) may limit the max-stable model’s ability at this site33. There are TGs where simulated AM surges are over/under-estimated (Fig. 2 and Supplementary Fig. 2). The maximum, mean, and minimum errors (root mean square errors, RMSE) between observed and median simulated AM surges of 40 TGs (except Key west) are 0.03, 0.13, and 0.25 m, respectively (Supplementary Figs. 2 and 3). The error for the Key west is 0.52 m, significantly higher than the other TGs. The model-simulated AM surges represent the observed spatial dependence of AM surges expressed by the pairwise madogram38 and extremal dependence coefficient39 (Supplementary Fig. 4).

Fig. 1: Performance of the max-stable model at the gauged locations.
figure 1

Relative differences (RD) of the max-stable model derived GEV location (a) and scale (b) parameters under leave-one-out validation compared to that of the univariate GEV distribution separately fitted to the AM surges at each TG.

Full size image
Fig. 2: Validation of the max-stable model.
figure 2

a–h Observed (black lines) and simulated (pink color) AM surges at the TGs not included in the model building identified in (i). i Locations of TGs not included in the model building indicated by the red stars markers and numbers, and the locations of the TGs (blue circles) used in max-stable model building.

Full size image

Assessing GEV parameters (i.e., return levels) prediction efficiency of the max-stable model is only possible at the gauged locations because ungauged locations do not have observation data. However, a surge reanalysis allows us to assess model efficiency at ungauged locations, though they are only an approximation of the real world and may perform poorly compared to the observations37. We sample the AM surges from the GTSR reanalysis at the TG locations, then fit the max-stable model to sample data and predict the GEV parameters at the ungauged location where GTSR provides data. We compare the predicted location and scale parameters with those computed by fitting individual GEV distributions to the GTSR data at all locations. Results (presented in Supplementary Fig. 5) indicate that the location and scale parameters are well reproduced at most locations, with median RDs of 0.27 and 0.48, respectively. Relatively higher errors in predicting location and scale parameters occur at locations where a sharp gradient exists in the GEV parameters of the GTSR data. For example, sharp gradients in the location parameter on the Atlantic coast of Florida and the North Pacific coast are reflected in the higher values of RDs in those regions. Similar regions with relatively higher RDs for the scale parameter exist in the North Atlantic, Atlantic coast of Florida, western GOM, and the North Pacific coast. For a more rigorous validation of the max-stable model, we have arbitrarily selected multiple TGs from different regions of the U.S. coastlines, which are not included in the model development due to limited records. We compare the observed AM surges at the selected TGs to the simulated AM surges of the corresponding closest grid locations (Fig. 2). The simulated time series of AM surges captures the overall temporal variability of the observed AM surges but shows an underestimation tendency for some cases. Results indicate the model’s ability to predict AM surges at ungauged locations.

Estimated GEV parameters from the max-stable model are used to compute the spatial surface of the return levels along the CONUS coastlines. Figure 3 illustrates the spatial distribution of 50-year and 100-year return levels estimated by the max-stable model along the CONUS coastlines and the return levels (c and d) computed by the single-site univariate GEV distribution. In accordance with the single-site return level estimates, the return levels calculated by the max-stable model are relatively lower along the west coast and the highest return levels occurred along the east coast. Spatial variations of return level magnitudes along the east coast, GOM, and west coast are apparent. The U.S. Atlantic and Gulf coasts are characterized by shallow bathymetry and wide continental shelf, provide favorable conditions for higher surges when strike by tropical cyclones (TCs). The tracks of TCs across the region often stretch along the entire southeast Atlantic coast from Florida to New Jersey due to the alignment of the coast, causing high storm surges40. In contrast, extra-tropical cyclones (ETCs) dominate the northeast Atlantic coast, causing relatively lower surges, while the high tidal ranges largely drives total water levels16,36. The model provides reasonable clusters of lower and higher storm surge return levels in the southwestern and southeastern Gulf coasts, respectively. This is intuitive given that the major hurricanes within the GOM mostly hit the southeastern coastlines of the GOM. Also, the model captures the north-south variation of the return level magnitudes along the west coast, i.e., the magnitudes decrease from north Pacific to south Pacific coast41.

Fig. 3: Spatial distribution of the storm surge return levels.
figure 3

50-year (a) and 100-year (b) return levels of storm surges (in meters) estimated from the max-stable model. 50-year (c) and 100-year (d) return levels of storm surges (in meters) estimated from the at-site GEV model.

Full size image

The median standard errors of the scale and location parameters for the max-stable model are 8 cm and 6 cm, respectively, indicating that the uncertainty associated with the estimated return levels is low relative to the return levels. In contrast, they are 19 cm and 15 cm for the single-site GEV model. We investigate the return level curves along with 95% confidence intervals for each tide gauge (Supplementary Fig. 6), indicating that the uncertainty bands of return level curves derived from the max-stable model are significantly lower than those derived from the single-site GEV model. Accurate estimation of distribution parameters in the classical single-site extreme value analysis is difficult because the short record length of sea level data measured at the tide gauges provides insufficient samples of extreme surge events (i.e., AM surges). This may lead to high uncertainty in distribution parameter estimates. In contrast, the max-stable model allows sharing information across sites by pooling extreme surge events from all selected tide gauges. Such data pooling drastically reduces uncertainty in distribution parameter estimates. The epistemic uncertainty associated with the classical site-by-site analysis is reduced by the model that employed max-stable process. The model reasonably captures the regional variability (east coast, GOM, and west coast) in the return levels as observed in the single-site GEV estimates while producing smooth return level surfaces by filling the spatial gaps and eliminating the limitations of data scarcity in coastal flood risk assessment. The model allows us to investigate coastal flood hazards at any location along the coastlines even though no tide gauge data is available.

Stochastic simulations provide 10,000 synthetic storm surge time series at each grid location42, allowing us to investigate the magnitudes and spatial extents of extreme events. Figure 4 illustrates the 2.5th, 50th, and 97.5th percentiles of simulated surge magnitudes and spatial extents of Hurricane Matthew in 2005 (left column), Hurricane Sandy in 2012 (middle panel), and Hurricane Katrina, Dennis, and Wilma in 2005 (right column). Time series plots (Fig. 4) represent the observed and simulated AM surges at the closest available TGs from the landfall locations of the corresponding hurricanes.

Fig. 4: Spatial extents of simulated AM surges for selected Hurricane events.
figure 4

Spatial extents of simulated AM surges (2.5th, 50th, and 97.5th percentiles) (in meters) for the selected extreme events: Hurricane Matthew (a–c), Hurricane Sandy (d–f), and Hurricane Katrina (g–i). Blue color lines present hurricane tracks. j–l Time series plots of observed (black lines) and simulated bands (2.5th and 97.5th) of AM surges for available TGs (black stars) at/near the hurricane landfall locations.

Full size image

Hurricane Matthew made landfall in October 2005 along the central coast of South Carolina after its first landfall as a major hurricane along the coasts of Haiti, Cuba, and the Bahamas. The spatial pattern of simulated AM surges follows the storm track extended from South Florida to South Carolina coasts. The corresponding time series plot at Charleston TG illustrates that the simulations well capture the observed AM surge in 2016 (1.64 m). The median simulated surge at the event is 1.41 m (2.5th and 97.5th percentiles are 1.11 m and 1.95 m, respectively). The simulated AM times series also capture similar extreme events with high efficiency and low uncertainty.

Hurricane Sandy struck New Jersey and New York coasts in October 2012. Hurricane Sandy was a special one due to its tremendously big size, which caused catastrophic storm surges in New York. It was reported that the surges were spatially distributed from Virginia to Maine, while relatively higher surges are evident from New Jersey to New York to Connecticut43. The simulated surges exhibit the spatial extents of surges from Hurricane Sandy. The highest surge observed at The Battery TG is 2.62 m. The 2.5th, 50th, and 97.5th surges in 2012 at The Battery TG are 1.57 m, 2.1 m, and 3.3 m, respectively. While the simulated AM surges capture extreme events, systematic underestimations are found for relatively lower surges.

In 2005, three hurricanes, i.e., Katrina, Dennis, and Wilma (among others), hit the northern Gulf of Mexico (GOM) and the South Florida region. Dennis (July 2005) landed on Santa Rosa Island, Florida, near Navarre Beach. Hurricane Wilma (October 2005) was identified as a category 3 hurricane when it made landfall in southwestern Florida near Cape Romano and crossed the southern Florida peninsula in 4.5 hr. Katrina (August 2005) was an extraordinary and one of the most devastating hurricanes first caused damage in South Florida as a category 1 hurricane and then made landfall on the northern Gulf coasts as a category 3 hurricane. The track of Katrina and favorable atmospheric and bathymetric conditions made Katrina extremely intense and exceptionally large resulted in longer extent of surges along the GOM and South Florida Coasts. Northeasterly middle to upper-level tropospheric flows forced Katrina to turn west-southwestward and made its first landfall in South Florida before it moved to southeastern GOM. Once in the water again after the first landfall, Katrina regained its energy and emerged to hurricane status. A huge upper-level anticyclone over the GOM resulted in weak wind shear and well-formed upper-level outflow favored Katrina’s rapid intensification. Katrina’s massive size of hurricane-force winds (peak intensity of 150 kt) extended up to about 90 nautical miles, caused widespread and devastating storm surges. Additionally, numerical experiment suggest that the unprecedented storm surge of Katrina was influenced by the extremely shallow continental shelf and ancient deltaic lobe of the Mississippi river, however, if would had taken a different track (i.e., the track of Hurricane Frederic), it might resulted in a much smaller surges than the observed in coastal Mississippi and Luisiana44,45. The simulated AM surges generate reasonable spatial patterns and extents for 2005 along the northern GOM and southwestern Florida coasts. Among the selected TGs, Pensacola is the closest to the landfall location of Katrina in the northern GOM. Though Dennis made landfall around this area in the same year, the Pensacola TG still experienced a higher surge during Katrina than Dennis (Supplementary Fig. 7); hence it is the best possible TG for analyzing Katrina’s surges. The time series of observed and simulated surges at the Pensacola TG are illustrated in Fig. 4, which depicts that the observed surge height in 2005 at this TG is 1.43 m while the median (50th percentile) simulated surge height is 1.79 m (2.5th and 97.5th percentiles are 1.36 m and 2.61 m, respectively).

Overall, the simulated surge magnitudes and their spatial extents are comparable to the observations and are consistent with the tracks and landfall locations of the hurricanes. As expected, the surges are relatively higher near the landfall locations and gradually get lowered as they are away from the landfall locations.

Conclusion

Quantifying coastal flood risks from extreme sea levels is critical for the sustainable management of infrastructure and socio-environmental systems in the coastal regions. Risk estimation requires accurately computing extreme event probabilities, which is often challenging due to the temporal and spatial sparseness of sea-level records. Hence, typically used site-by-site analysis of extreme event probabilities holds high uncertainty and does not provide information for ungauged locations. Storm surge reconstructions and regional frequency analysis may partially address the limitations but introduce new weaknesses (e.g., discontinuous, and unsmooth surfaces of extreme event probabilities). In contrast, we have used max-stable models, which leverage extreme sea level records (AM surges) from all selected tide gauges, leading to a more accurate and reliable estimation of distribution parameters and continuous spatial field of extreme event probabilities. Our modeling framework enables us to compute return level magnitudes of extreme events and simulate synthetic AM surge time series at any location along the CONUS coastlines. The model substantially reduces the uncertainty (i.e., standard errors) in distribution parameter estimates, thereby in return levels.

Despite the promising results, the simulation of AM surges computed in this study employing the max-stable model has multiple limitations and challenges. First, there is no true data to validate the model estimates at the ungauged locations; however, the leave-one-out validation and investigating model performance at ungauged locations using reanalysis surge data ensure that the model performs reasonably well in predicting GEV parameters. Besides, the model results at the ungauged locations are validated against the observed of AM surges of the closest TGs, which are not included in the model development due to short records. We investigate the spatial extent and magnitude of AM surges and return levels (50- and 100-year) at gauged locations obtained from the tide gauge observations, max-stable model, and storm surge reanalysis data (i.e., GTSR and CoDEC data). Results illustrate differences in storm surge results between the max-stable model, GTSR, and CoDEC data, yet the max-stable model performs better in capturing the observations (please check the Supplementary Discussion and Supplementary Figs. 8 and 9 for details). However, our model did not capture wind-localized variability of surges to some extent because the max-stable process is designed to generate smooth spatial fields of extremes, and the model is not equipped to explicitly analyze the wind-driven part of the extreme surges. The max-stable model shows a limited ability to predict the location and scale parameters of the GEV distribution for the TGs (e.g., Key West) located at a longer distance from the nearby TGs and having significantly different variances in the AM surges compared to that of the nearby TGs. The spatial structure of GEV parameters is driven by the climatological dependence, whereas the coherence between AM surges of nearby TGs and their gradual reduction from the landfall location of storms (e.g., tropical and extra-tropical cyclones and atmospheric rivers) depends on the spatial extent of individual events. Therefore, reordering the stochastically simulated storm surges to the observed ranks at gauged locations, and the weighted average ranks (of adjacent TGs) at ungauged locations are valid approaches. The model can generate synthetic AM surges at ungauged grid locations to help investigate the temporal variability of AM surges and the spatial extent of any event. The current form of the model cannot forecast AM surges; however, it can be extended to a forecast model by including a rank forecast model employing the learning-to-rank techniques46. Instead, the study focuses on simulating the synthetic series of AM surges.

The study provides spatial fields of return levels and synthetic time series of AM surges at the gauged and ungauged locations along the CONUS coastlines. Most notably, the study generates more meaningful estimates for the areas with no or minimum sea level data available. The results will help coastal planners, engineers, and stakeholders to make the most precise and confident decisions. Other scientists will also use the study outputs (return levels and synthetic series of AM surges) to investigate the spatiotemporal variability of extreme surges, quantify flood risks and economic losses, and select suitable and appropriate flood reduction measures.

Methods

Data

Hourly sea level data are collected from the Global Extreme Sea Level Analysis—version 3 (GESLA-3; https://gesla787883612.wordpress.com/) and the National Oceanic and Atmospheric Administration (NOAA; https://tidesandcurrents.noaa.gov/) database. The NOAA database provides the most rigorous spatial and temporal coverage for the US coastlines, hence considered the primary source of the data. We filter out the tide gauges with no data beyond 1950 and more than 20% missing over the entire record. This deduces 41 tide gauges along the contiguous US coastlines, finally used in the analysis. The sea level data used in this study are provided in meters relative to the station datum (STND). First, we detrend the hourly sea level time series by removing the annual mean sea levels (MSL). Next, we remove tides from the hourly time series by predicting the tide by performing a classical harmonic analysis year-by-year with 67 tidal constituents using the T-tide Matlab package47. From the non-tidal residual (i.e., after removing annual MSL and tides), we employ the block maxima approach to prepare the annual maximum storm surge time series at each selected tide gauge. Two storm surge reanalysis datasets, produced by the physics-based hydrodynamic models, namely the Global Tide and Storm Surges (GTSR)34 and the Coastal Dataset for the Evaluation of Climate Impact (CoDEC)35 are used to validate our model. The National Hurricane Center’s Hurricane Database (HURDAT2)48 for the Atlantic Basin is used to identify the tracks of the selected tropical cyclones and investigate how the model simulate storm surges at and around the landfall locations.

Modeling of extreme surges

This study develops a framework to support estimating the exceeding probabilities of extreme surge events at any location along the CONUS coastlines by filling the spatial gaps between tide gauges with the stochastically generating storm surge extremes. The max-stable model is used to derive the spatial field of GEV distribution parameters, which are then used to stochastically generate AM surges at gridded locations along the CONUS coastlines. Finally, the synthetic AM surge series are temporally reordered following the observed ranks to incorporate the spatiotemporal variability. Our model allows us to estimate both the GEV parameters and simulate the AM surges at any arbitrary locations, either gauged or ungauged. The details of the methods are discussed in the following sections.

Classical and max-stable process models for extremes

Univariate extreme observations (e.g., AM surges) of \({Y}_{t}=\max \{{Y}_{1},{Y}_{2},\ldots ,{Y}_{t}\}\), where \({Y}_{1},\ldots ,{Y}_{t}\) is a sequence of independent observations having a common statistical distribution function can be defined by the GEV with the following distribution function:

$$G\left(Z\right)=\exp \left\{-\left[1+\xi {\left(\frac{z-\mu }{\sigma }\right)}^{-1/\xi }\right]\right\}$$
(1)

Where \(\mu\) and \(\sigma\) are the location and scale parameters of GEV distribution, respectively. The shape parameter is represented by \(\xi\), which determines the tail of the distribution. Based on the shape parameter values, the distribution can correspond to Weibull \((\xi \, < \, 0)\), Gumbel \((\xi =0)\), and Fréchet \((\xi \, > \, 0)\) sub-family of distributions. The values corresponding to any probabilities can be predicted via inversion of the distribution function. GEV distribution is commonly used for extreme storm surge analysis, while Generalized Pareto distribution has also been used in many studies7,11,16.

In order to extend the classical univariate GEV to a multivariate domain (i.e., spatial GEV), earlier research proposed modeling spatial dependence employing hierarchical models49; however, they generally do not account for data-level dependence. In contrast, the max-stable process extends the univariate GEV model to the multivariate spatial domain, which resolves the limitations of the classical spatial GEV model. The max-stable process holds a framework for modeling multivariate extremes considering spatial and temporal dependence. Let \({Y}_{t}\left(S\right),{t}=1,\ldots ..,t\), be the independent realizations of a continuous process (i.e., AM surges) for year \(t\) and at location \(S\), where \(S={s}_{1},{s}_{2},\ldots .{s}_{n}\) represents the locations of the TGs existing in a spatial domain is a max-stable process with GEV marginals if the following limit exists jointly for all TGs:

$${Y}_{t}\left(S\right)=\mathop{{{{{\mathrm{lim}}}}}}\limits_{t\to +{\infty }}\frac{{\max }_{t=1}^{t}{Y}_{t}\left(s\right)-{b}_{m}(s)}{{a}_{m}(s)}$$
(2)

Where \({a}_{m}\left(s\right) \, > \, 0\) and \({b}_{m}(s)\) are normalizing constants. Observed pairwise extremal coefficients are used to calibrate the max-stable process. The observed pairwise extremal coefficient is computed using the modified madogram, the F-madogram50:

$${\nu }_{F}\left({s}_{1}-{s}_{2}\right)=\frac{1}{2t}\mathop{\sum }\limits_{i=1}^{t}\left|F\left({z}_{i}\left({s}_{1}\right)\right)-F\left({z}_{i}\left({s}_{2}\right)\right)\right|$$
(3)

Where \({z}_{i}\left({s}_{1}\right)\) and \({z}_{i}\left({s}_{2}\right)\) are the ith observations (the AM surges in the ith year) of the random field at location \({s}_{1}\) and \({s}_{2}\) and \(t\) is the total number of observations (i.e., years). The observed pairwise extremal coefficient \(\hat{\theta }\) is then estimated by:

$$\hat{\theta }\left({s}_{1}-{s}_{1}\right)=\frac{1+{2\nu }_{F}\left({s}_{1}-{s}_{2}\right)}{1-{2\nu }_{F}\left({s}_{1}-{s}_{2}\right)}$$
(4)

Finally, the max-stable process is fitted by minimizing the sum of squared errors between the theoretical and modeled pairwise extremal coefficients. We fit a max-stable process to the 68 years of AM surge time series of the selected 41 TGs from 1950 to 2017 along the CONUS coastlines. We tested different model settings in fitting the max-stable process and identified the best model using the Takeuchi Information Criterion (TIC) which is analogous to Akaike Information Criteria (AIC) but employs maximum pairwise likelihood estimators instead of maximum likelihood estimators51. Let, \({L}_{i,j}\left({x}_{i,j},\theta \right)\) the likelihood for TG \(i\) and \(j\), where \(i={{{{\mathrm{1,2}}}}},\ldots ,N-1{;\; j}=i+1,i+2,\ldots ,N\). \(N\) is the number of TGs within the region and \({x}_{i,j}\) are the joint observations for TG \(i\) and \(j\). The pairwise likelihood \({PL}\left(\theta \right)\) is defined by.

$${L}_{P}=\log {PL}\left(\theta \right)=\mathop{\sum }\limits_{i=1}^{N-1}\mathop{\sum }\limits_{j=i+1}^{N}\log {L}_{i,j}\left({x}_{i,j},\theta \right)$$
(5)

The pairwise likelihood is an approximation of the “full likelihood”; hence the standard errors are estimated using a sandwich estimates as:

$$\hat{\theta } \sim N\left(\theta ,{H}^{-1}\,J{H}^{-1}\right)$$
(6)

Where \(H\) is the Fisher information matrix and \(J\) is the variance of the score function30. The parameters (\(\theta\)) included in model are the GEV distribution parameters (i.e., location, scale, and shape) and the spatial dependence parameters (e.g., sill, nugget, and range). The model optimizes the parameters and provides associated standard errors, which in turn are used to quantify return levels and associated uncertainty. The location and scale parameters are modeled spatially in different model settings as linear/non-linear/semiparametric functions of longitude, latitude, and bathymetry. This is based on the fact that the storm surge is a spatially continuous process, which varies smoothly along the coastlines depending on the scales of surge generating weather regimes15,52. On the other hand, surges may be spatially discrete due to local bathymetric features and shelf geometry53,54. The shape parameter is assumed to be constant over the entire spatial domain, an assumption often considered in extreme value analysis because of its strong sensitivity to GEV fit13,16. The best-fitted max-stable process model estimates GEV parameters at the gauged and ungauged locations. The ungauged grid locations for the CONUS coastlines are extracted from the high-resolution grid locations provided by the Global Self-consistent, Hierarchical, High-resolution Geography Database (GSHHG)55. Spatial distances between subsequent GSHHG grid locations vary depending on the shape of the coastlines and Euclidean distances vary from 0.05° to 0.75° (average is 0.31°) (Supplementary Fig. 1).

Simulation of annual maximum (AM) surges

We stochastically simulate AM surges (10,000 synthetic time series) at each grid location along the CONUS coastlines using the max-stable model predicted GEV parameters. Spatiotemporal variability of the observed AM surges is incorporated by temporal reordering of the simulated AM surges to match the rank of the observed AM surges (i.e., rank-ordering) at each TG. This resampling in rank space has been successfully implemented in various hydrological applications (e.g., time series generation, flood forecasts, ensemble forecasts, and ensemble postprocessing) where spatiotemporal variability is important56,57,58,59,60,61,62.

For the ungauged grid locations, we first apply the weighted distance average of the observed AM surge ranks of the two adjacent TGs to compute the ranks at the ungauged grid locations and then use the computed ranks to reorder the simulated AM surges at those locations. We assume that the statistical characteristics (e.g., interannual variability) of AM storm surges at an ungauged location are more likely to be that of the nearest TG. The closer the grid location is to the TG, the more similar the statistical characteristics. This assumption is supported by the fact that an extreme surge event during a storm (tropical cyclone, extra-tropical cyclone, or atmospheric river) covers a long stretch of coastline and the surge magnitude reduces with the distance away from the landfall location36,52,63.

Validation of the max-stable model and AM surge simulations

To validate the model performance in quantifying the GEV parameters at each tide gauge, we exclude one TG at a time (i.e., leave-one-out), calibrate the max-stable model using the AM surges of the rest of the TGs, then predict the GEV parameters of the omitted TG. We repeat this procedure and predict GEV parameters for each of the selected 41 tide gauges. The max-stable model predicted GEV parameters (location and scale) obtained from the leave-one-out validation are compared with those obtained from the max-stable models fitted to all TGs data. Though the site-specific location and scale parameters estimated by univariate GEV are not exactly the true values, comparing model predictions at those locations provides an opportunity to assess max-stable model efficiency in estimating marginal behavior64,65. Hence, the predicted GEV parameters (from the leave-one-out experiment) are also compared to the location and scale parameters of each TG estimated by univariate GEV distribution. To evaluate the model performance in estimating GEV parameters, a skill statistic called relative difference (RD) is defined as \({{{{{{\rm{RD}}}}}}}=\left|\frac{{Y}_{{{{{{{\rm{actual}}}}}}}}-{Y}_{{{{{{{\rm{model}}}}}}}}}{{Y}_{{{{{{{\rm{actual}}}}}}}}}\right|,\) where \({Y}_{{{{{{{\rm{actual}}}}}}}}\) and \({Y}_{{{{{{{\rm{model}}}}}}}}\) are the true and estimated values of the parameters, respectively. The estimated GEV parameters are used to quantify the return levels of extreme surges. Return levels are often used in the engineering design of coastal flood protection infrastructure (e.g., sea walls, dikes, and sand dunes). An N-year return level can be estimated using the quantile function of GEV distribution as \({F}^{-1}=\left(1-\frac{1}{N};\mu ,\sigma ,\xi \right)\), where F−1 is the inverse cumulative distribution function for the fitted GEV distribution. We further assess our proposed model’s performance against observational data for select years with extreme tropical cyclone activity (Katrina 2005, Sandy 2012, and Matthew 2016). For this purpose, we compare the surge heights at (near) the landfall locations and the spatial extents of surges around the landfall locations with the model simulations. Furthermore, the model’s ability to reproduce the temporal variability of AM surges at ungauged locations is assessed. To do so, we consider the tide gauges that are not included in the model calibration due to short record length and compare the model simulated and observed AM surges at those tide gauges over the (recent) years for which data are available. If the selected tide gauge and the model grid location do not coincide, we select the model grid location close to the corresponding tide gauge location.