Topological pumping in Aharonov–Bohm rings

Abstract

Topological Thouless pumping and Aharonov–Bohm effect are both fundamental effects enabled by the topological properties of the system. Here, we study both effects together: topological pumping of interacting particles through Aharonov–Bohm rings. This system can prepare highly entangled many-particle states, transport them via topological pumping and interfere with them, revealing a fractional flux quantum. The type of the generated state is revealed by non-trivial Aharonov–Bohm interference patterns that could be used for quantum sensing. The reflections induced by the interference result from transitions between topological bands. Specific bands allow transport with a band gap scaling as the square-root of the particle number. Our system paves a new way for a combined system of state preparation and topological protected transport.

Introduction

Topological matter defines an important field in fundamental physics with far reaching implications for quantum technology: the correlations encoded in the topological matter are a precious resource for quantum technology; at the same time, quantum technology can be exploited to study topological matter with unprecedented precision and control ^1,2,3,4. Among the several important contributions given by David Thouless in this field, the idea of topological pumping is particularly relevant for quantum technology: charge is transported through a one dimensional system using the topological band structure of an extended (many-body) system^5,6. This is realized by driving the system periodically in time while protecting the band gaps.

Topological pumping has been studied experimentally in various systems, including cold atoms^7,8,9, photonic waveguides¹⁰ and superconducting circuits¹¹. Due to interference effects, topological pumping displays very interesting features in ring-shaped networks^12,13. Here, we couple topological bands in interacting Aharonov–Bohm (AB) rings attached to leads. The lead-ring interfaces act as non-linear beam-splitters. We demonstrate how interaction in such beam splitters can generate highly entangled states, that can be revealed through interference patterns characterized by a fractional flux quantum.

Among other quantum technology implementations, we want to highlight Atomtronics: cold atoms matter-wave circuits^14,15,16,17 guided by laser generated fields to realize arbitrary potential configurations. These systems have reduced decoherence rate due to charge neutrality, and allow one to manipulate carrier statistics and inter-atom interaction. Rectilinear circuits have been used to study quantum transport^18,19,20,21. More complex networks can be fabricated, trapping Bose–Einstein condensates in versatile potentials. Such potentials can be changed in shape and intensity at time scales of tens to hundreds microseconds, and therefore opening the way to modify the features of the circuit in the course of the same experiment (typically involving tens of milliseconds)^{22,23,24,25,26,27,28,29,30,31,32,33,34,35}. Such remarkable advances on the flexibility and control of cold-atoms quantum technology, in turn, has been opening up exciting possibilities for atomtronics to study transport. Previous studies on bosonic AB attached to leads have demonstrated that fundamentally new effects emerge^36,37. We shall see that, accordingly, topological pumping in these networks displays peculiar features as well.

We now summarize our results. The system is characterized by topologically distinct bands that can be controlled by changing the parameter of the driving (its phase ${\phi }_{0}$). We investigate the limit where the lattice potential is sufficiently large so that particles are confined to each site during the transport.

Our device works as a non-linear interferometer, in which the source-ring and the ring-drain interfaces act as “beam-splitters". We identify the mechanism behind the AB effect in topological pumped systems with interaction: AB interference affects particle reflections by inducing specific transitions between the topological bands. Interaction adjusts the transmission and the reflection coefficients. In addition, it can create NOON-type entanglement comprising of particles being in upper and lower arm of the ring.

The speed of state preparation in our protocol is limited by the band gap and Landau–Zener transitions between bands. The topological pumping through the two branches forming the anti-crossing is bound to be characterized by two different mechanisms: Pumping through the upper (lower) branch occurs via off-resonant (resonant) tunneling. Our result shows that the transport of $N$ particles is best done in the lowest band since the band gap here scales as $\Delta E\propto \sqrt{N}$ (the band gap in the upper band decreases exponentially with $N$ instead).

The states are transported through the ring, and interfere at the ring-drain interface; this results in a partial transmission of the particles, which is modified by the applied AB flux. We observe that the periodicity of the flux is reduced compared to its single particle value depending on the type of (entangled) state and particle number. This suggest that the flux quantum ${\Phi }_{0}$ becomes a fraction of its single-particle value³⁸. Specifically: in the lowest topological band, even number of particles are transmitted independently of the flux while odd number of particles show AB oscillations; in the highest topological band, AB flux periodicity changes with particle number due to the formation of NOON-like entangled states; in the central band, different types of partial transmission and (entangled) states occur depending on the initial phase shift of the driving and the length of the ring. Entangled states of NOON-type of several particles can be created with nearly unit fidelity.

Results

The setup

A sketch of the ring-lead system is presented in Fig. 1a. It is composed of a lattice ring attached to two leads (source and drain) symmetrically at two opposite sites of the ring loaded with $N$ particles.

Fig. 1

Description of setup. a Sketch of the ring-lead system. The dots indicate lattice sites $j$ with a space and time-dependent potential ${V}_{j}(t)={P}_{0}\cos (2\pi /3j-\Omega t)$ with a period of three lattice sites (${\text{A}}:\, j=0$, ${\text{B}}:\, j=1$, ${\text{C}}:\, j=2$). Particles tunnel between different sites along the black lines with strength $J$. $U$ denotes the on-site interaction and $\Phi$ the flux of the ring. With topological pumping, particles can be transported from the initial position through the ring to the target drain position. The circled lead-ring junctions act as effective beam-splitters of incoming particles. b Topological pumping of particles on lattice sites by adiabatic modulation of the periodic potential ${V}_{j}(t)$ with Chern number ${\mathcal{C}}=-1$. The cosine potential (black line) is varied adiabatically in time $t$ with a frequency $\Omega =2\pi /T$, where $T$ is the time of one driving period. Particles are initialized at $\text{A}$. At time $t=0$ no tunneling occurs due to a large potential difference to neighboring sites. At time $t=1/6T$, potential at $\text{A}$ and $\text{B}$ becomes degenerate, and particles are adiabatically transferred to $\text{B}$. This process continues and after one period $T$ the particles have moved by $3{\mathcal{C}}$ sites

One particular experimental realization is possible using a combination of experimentally demonstrated technologies for cold atom systems. Spatial light modulators and digital mirror devices (DMD) can be employed to generate arbitrary light fields in a 2D plane^32,39,40. With DMD, the potential can also be dynamically varied with a refresh rate of tens of $\mu$s. Similar structures can also be achieved by painting these geometries with a focused laser beam³⁴. A confinement in a 2D plane is realized by an additional blue detuned standing wave lattice²⁵. These technologies would enable the experimental realization of the proposed confining structures with feature sizes limited by the optical resolution. With these technologies, a ring lattice of tens of atoms, with a typical lattice spacing of few $\mu$m has been realized²⁵. The phase of the confined atoms for artificial gauge fields can be manipulated by direct phase imprinting⁴¹ or transferred with a two-photon Raman transition⁴².

Superconducting cavities with microwave photons can realize Bose–Hubbard Hamiltonian, while allowing full control of the cavity potentials and even couplings in time^11,43. Ring structures and synthetic magnetic fields have been realized⁴⁴.

Our model lead-ring Hamiltonian is ${\mathcal{H}}={{\mathcal{H}}}_{\text{R}}+{{\mathcal{H}}}_{\text{S}}+{{\mathcal{H}}}_{\text{D}}+{{\mathcal{H}}}_{\text{I}}+{{\mathcal{H}}}_{\text{P}}$. The ring Hamiltonian is

$${{\mathcal{H}}}_{\text{R}}=-{\sum }_{j=1}^{{L}_{\text{R}}}\left(J{e}^{i2\pi \Phi /L}{\hat{a}}_{j}^{\dagger }{\hat{a}}_{j+1}+\,\text{H.C.}\right)+\frac{U}{2}{\sum }_{j=1}^{{L}_{\text{R}}}{\hat{n}}_{j}^{\,\text{a}\,}({\hat{n}}_{j}^{\,\text{a}\,}-1),$$

(1)

where ${\hat{a}}_{j}\,({\hat{a}}_{j}^{\dagger})$ are the annihilation (creation) operator at site $j$ in the ring, ${L}_{\text{R}}$ the number of ring sites, ${\hat{n}}_{j}^{a}={\hat{a}}_{j}^{\dagger }{\hat{a}}_{j}$ is the particle number operator of the ring, $J$ is the inter-site hopping, $U$ is the on-site interaction between particles and $\Phi$ is the total flux through the ring. Periodic boundary conditions are applied for the ring with ${\hat{a}}_{{L}_{\text{R}}}^{\dagger }={\hat{a}}_{0}^{\dagger }$. In the following, we set $J=1$ and all values of $U$, $\Omega$ are given in units of $J$. The Hamiltonian for the source (similar for drain ${{\mathcal{H}}}_{\text{D}}$) is given by

$${{\mathcal{H}}}_{\text{S}}=-{\sum }_{j=1}^{{L}_{\text{S}}}\left(J{\hat{s}}_{j}^{\dagger }{\hat{s}}_{j+1}+\,\text{H.C.}\right)+\frac{U}{2}{\sum }_{j=1}^{{L}_{\text{S}}}{\hat{n}}_{j}^{\,\text{s}\,}({\hat{n}}_{j}^{\,\text{s}\,}-1),$$

(2)

where ${L}_{\text{S}}$ (${L}_{\text{D}}$) is the length of the source (drain) and ${\hat{s}}_{j}$ (${\hat{d}}_{j}$) the source (drain) annihilation operator. We set ${L}_{\text{S}}={L}_{\text{D}}=1$ in the following. The coupling Hamiltonian between leads and ring is ${{\mathcal{H}}}_{\text{I}}=-J\left({\hat{a}}_{0}^{\dagger }{\hat{s}}_{0}+{\hat{a}}_{{L}_{\text{R}}/2}^{\dagger }{\hat{d}}_{0}+\,\text{H.C.}\,\right)$. We modulate the potential landscape adiabatically to pump particles

$${{\mathcal{H}}}_{\text{p}}(t)={P}_{0}{\sum }_{j}\cos \left(\frac{2\pi j}{3}-{\phi }_{0}-\Omega t\right){\hat{n}}_{j}^{},$$

(3)

with the driving frequency $\Omega$, the particle number operator ${\hat{n}}_{j}^{}$ and phase shift ${\phi }_{0}$. The potential has a period of three sites and its arrangement in the ring-lead system is shown in Fig. 1a. In the case of zero interaction and no flux, the Hamiltonian is known to be topological nontrivial. The system has three bands and non-zero Chern numbers⁶ (top band +1 and bottom band −1 with Chern number ${\mathcal{C}}=-1$ and central band 0${}^{\pm }$ with ${\mathcal{C}}=2$). The pumping is induced by breaking time-translational symmetry via driving. The topological properties hold true even in the interacting case^11,45. Similar systems have been studied in refs. ^11,46. After one period of adiabatic time evolution $T=2\pi /\Omega$, particles move by $3{\mathcal{C}}$ sites (see Fig. 1b). The protocol is as follows: Initially, a Fock state with $N$ particles at a single site in the source lead is prepared. Here, we initialize the particles at the first source lead site that directly neighbors the ring and tune ${\phi }_{0}$ to select the band (see Fig. 1a).

In the following, we investigate positive interaction ${U}\, {> }\, 0$ without loosing generality. For U < 0, simply switch the results of band +1 with −1, and 0⁺ with 0⁻. We operate in the limit of ${P}_{0}\gg J,U$, such that the eigenstates are strongly localized within single sites. Thus, tunneling between neighboring sites is suppressed unless close to a resonance (since they have in general a widely different local potential energy), as well as effective tunneling across three sites (to the nearest site with the same potential). The effective tunneling dynamics can be understood in this limit by including the nearest neighboring site only. We define the transmitted density as the expectation value of the number of particles in the drain at the time the particles arrive in the drain (see final position in Fig. 1a).

Non-interacting topological pumping

First, we discuss the single-particle dynamics for the ring-lead system. The particles are prepared in the source at a single site as shown in Fig. 1a. The dynamics of the non-interacting case is plotted in Fig. 2. We investigate two cases: For bands $\pm 1$ with Chern number ${\mathcal{C}}=-1$, and band 0 with ${\mathcal{C}}=2$. We highlight that the dynamics both bands $\pm {\!}1$ are identical. We now evolve the system under the time-dependent Hamiltonian. The particles are transported towards the ring via adiabatic driving. The speed depends on the Chern number of the respective band. At the ring, the path splits into two ways: The upper and lower part of the ring. Here, the particles split into a superposition state, going along both paths at the same time. At the end of the ring, the two paths merge and interfere. We can control this interference using the artificial magnetic flux $\Phi$. Depending on $\Phi$, we observe constructive or destructive interference. For constructive interference, particles leave the ring and move into the drain. For destructive interference at $\Phi =1/2$, particles are reflected. In this case, we observe that the particles move back the way they came at a different speed. If the particles are initially in a band with Chern number ${\mathcal{C}}=-1$, the reflection occurs via the band with ${\mathcal{C}}=2$, and vice versa. From this, we can understand the mechanism how reflections in topological pumped AB rings arise: Reflections caused by destructive AB interference arise by transferring particles to bands with a Chern number of opposite sign. However, we find that these AB reflections occur independently of the driving frequency, indicating that they are distinct from Landau–Zener transitions. We can understand the reflection and transmission by looking at the dynamics at a reduced lead-ring junction consisting only of three sites: two sites of the ring ($\left|{C}_{1}\right\rangle$ and $\left|{C}_{2}\right\rangle$) connected via hopping to a single drain site ($\left|B\right\rangle$). This reduced three site system is a three level system for zero interaction, akin to the well known $\Lambda$-system. One of its eigenstates is a dark eigenstate $\left|D\right\rangle =\frac{1}{\sqrt{2}}(\left|{C}_{1}\right\rangle -\left|{C}_{2}\right\rangle )$, that always has zero amplitude at the drain site for any value of the driving parameter $\phi (t)$. Conversely, there is also a bright eigenstate that will adiabatically tunnel from the two input sites over to the drain site. Particles can only tunnel over if they are in a bright eigenstate, and are prohibited from tunneling if they are in the dark state. We calculate the dynamics of an incoming superposition state $\left|{\Psi }_{\text{in}}\right\rangle =1/\sqrt{2}(\left|{C}_{1}\right\rangle +{e}^{i2\pi \Phi }\left|{C}_{2}\right\rangle )$, which is initialized in the two input sites and then adiabatically pumped. The transmission probability is given by the overlap with the bright state, and the reflection probability (the probability of not reaching the drain site) is the overlap of the incoming superposition state with dark eigenstate $R={\left|\langle {\Psi }_{\text{in}}(\Phi )| {\Psi }_{\text{dark}}\rangle \right|}^{2}$. The overlap depends on the phase of the superposition state, which is controlled by flux $\Phi$. The reflection probability of this three level system is $R={\sin }^{2}(\pi \Phi )$ and the transmission probability $T=1-R={\cos }^{2}(\pi \Phi )$. For a single particle or $U=0$ the flux dependence and smallest energy gap $\Delta E=2J$ is the same for all bands. The speed of pumped particles solely depends on the Chern number of its band.

Fig. 2

Pumping for non-interacting ring. Time evolution of topological pumping of non-interacting particles in the ring-lead system with ring length ${L}_{\text{R}}=6$, $N=1$ particles and potential strength ${P}_{0}=60J$. Initial band has a, b Chern number ${\mathcal{C}}=-1$ (driving frequency $\Omega =0.01J$, phase shift ${\phi }_{0}=0$) and c, d Chern number ${\mathcal{C}}=2$ ($\Omega =-0.01J$, ${\phi }_{0}=\pi /2$). a, c Show flux $\Phi =0$, b, d show flux $\Phi =1/2$. Flux $\Phi =1/2$ causes total reflections; the particles are transferred to a band with Chern number of opposite sign and different velocity (b) initially in ${\mathcal{C}}=-1$, reflected particle in ${\mathcal{C}}=2$). Y-axis depicts ring-lead system sites, with site 0: source, site 1–6: ring, site 7: drain. Sketch of ring is shown on the top left. e, f Density in source and drain against time for different values of flux and Chern number e ${\mathcal{C}}=-1$ and f ${\mathcal{C}}=2$

Interacting topological pumping

We now turn to the case of non-zero interaction. While topological pumping was defined above for non-interacting systems, we find the same Chern numbers (how many sites particles travel in a band per period) even for the interacting system in our configuration. We believe our approach does work because our protocol can pump bound states of $N$ particles (instead of bare particles), which retain the topological properties of the non-interacting particles. For increasing interaction $\left|U\right|$, many-body effects come gradually into play. Once the interaction ${U}\, {> }\, \Omega$ is larger than the driving speed $\Omega$, the energy splitting between different many-body states is large enough such that it is not washed out by the driving. In this regime, we observe a many-body AB effect.

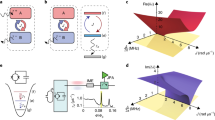
Then, the transmission and reflection through the ring substantially depends on the band and the sign of $U$. The pumping mechanism with interaction is described in Fig. 3. Pumping for a non-interacting system is described in Fig. 3a. Particles tunnel from one site to the next at the anti-crossings of the band (see Fig. 3b). With interaction, there is an asymmetry in the pumping mechanism for top and bottom level of the anti-crossing. Interaction pushes most of the uncoupled many-body levels downwards and closer together in energy, while the top two levels are further detached from the other levels. Thus, with nearest-neighbor coupling, the bottom level of the anti-crossing transports states resonantly via intermediate states, while the top level transport occurs off-resonantly without occupying those intermediate states. The top band has an exponentially suppressed gap with particle number, while for bottom band it increases with particle number. Transmission and reflection for interacting particles are governed by this asymmetry at the ring-lead interface (see Fig. 3c). The many-body AB effect changes transmission and reflection by at most one particle, e.g. for band +1 in between $N$ to $N-1$ particles are transmitted depending on flux. The functional dependence is similar to the non-interaction AB effect, e.g. for band +1 it is $T=N-1+{\cos }^{2}(\pi \Phi N)$, where $N$ is the particle number. Note that in this case the interaction reduces the periodicity with flux compared to the non-interacting case, with a flux quantum of ${\Phi }_{0}=1/N$. A full list is shown in Table 1. Additionally, the energy gap becomes dependent on band, interaction and particle number. In particular, the symmetry of bands $\pm 1$ is broken, and they behave differently. Additionally, band $0$ changes its behavior depending on the initial phase ${\phi }_{0}$.

Fig. 3

Pumping mechanism. a Energy spectrum of three bands for topological pumping in a lattice, with potential ${V}_{j}(t)={P}_{0}\cos (2\pi /3j-\phi (t))$, $\phi (t)={\phi }_{0}+\Omega t$ with a period of three sites ($\,\text{A:}\,\ j=0$, $\,\text{B:}\,\ j=1$, $\,\text{C:}\,\ j=2$). Particles are initialized at site $\text{A}$. By adiabatically changing phase $\phi (t)$ particles follow the band, moving along $A$-$B$-$C$ across the system. The energy gap for interaction $U=0$ is $\Delta {E}_{0}=2J$ for all bands. b Close-up of the interacting many-body eigenlevel structure (for repulsive interaction $U\,\, > \,\,0$) of any band anti-crossing (at exemplary circled area in a). We show the eigenlevel structure of two neighboring sites $j$ and $j+1$ as solid lines (decoupled system $J=0$ as dashed lines). $\left|30\right\rangle$ denotes a state with 3 particles at site $j$ and 0 particles at site $j+1$. Band +1 follows top curve of the anti-crossing, while band −1 follows bottom curve. Band 0 switches at every anti-crossing between top or bottom curve (see a). For the top curve of anti-crossing, the energy gap to the next eigenstate is scaling as $\Delta {E}_{1}\propto {J}^{N}/{U}^{N-1}$ for $U\gg J$. The transport occurs due to off-resonant coupling of the final states ($\left|30\right\rangle$ and $\left|03\right\rangle$ for $N=3$) via off-resonant intermediate states ($\left|21\right\rangle ,\left|12\right\rangle$) which are barely occupied. For the bottom curve, the energy gap is $\Delta {E}_{2}=2\sqrt{N}J$ for $U\gg J$. Transport occurs via resonant transitions to intermediate states ($\left|21\right\rangle ,\left|12\right\rangle$) which are significantly occupied. c Pumping through the lead-ring junction (consisting of a site $\,\text{B}\,$ connected to two sites ${\text{C}}_{1}$ and ${\text{C}}_{2}$). This three site system effectively acts as a non-linear beam-splitter. Adiabatic driving of the two types of transitions will produce different final states. Phase of resulting state depends on the complex tunneling strength $J{e}^{i\alpha }$ due to the flux $\Phi$. The top curve of the anti-crossing gives entangled states, which pick up a phase $\propto N$ due to the NOON-type entanglement. Bottom curve yields states that depend on the parity of the particle number $N$, which either pick up a phase factor (odd $N$) or none (even $N$)

Table 1 Overview of results

Lower band −1

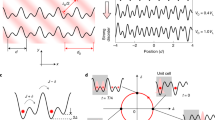
Here, we choose initial phase shift ${\phi }_{0}=\pi$. In this case, the avoided crossing is approached from below. The particle transfer from one site to the next is found to happen via resonant transitions to intermediate many-body states when these states become resonant. For $U\gg J$, the energy gap is independent of $U$: $\Delta E=2\sqrt{N}J$. This shows that the pumping can be driven at higher frequency with increasing particle number $N$ (see Supplementary Note 1). In this regime, we find that the pumping is dependent on the parity of the particle number $N$. The dynamics for different particles numbers is plotted in Fig. 4. For $N=2n+1$ we find a fractional transmission with flux: For zero flux, all particles are transported to the drain (uppermost site) (Fig. 4a). However, for half-flux, one particle is reflected and the rest is transmitted (Fig. 4b). The back-reflection occurs at twice the speed via the central band with Chern number ${\mathcal{C}}=2$. The density in the drain for odd $N$ is plotted in Fig. 4c. In contrast, for even $N=2n$ all the particles reach the drain independently of the flux (Fig. 4d). To understand the parity effect, we investigate the type of Fock states generated at the ring-lead junction. We denote the wavefunction of a single particle localized in the upper half of the ring as $\left|\cap \right\rangle$, and $\left|\cup \right\rangle$ in the lower half of the ring. The Fock states are generated by the resonant tunneling process at the ring-lead junction, where the path splits into two directions. Here, particles tunnel one after the other. The process favours the state with the lowest interaction energy; thus, the system tries to achieve a state with an equal number of particles in each arm. For $N=2n$, such a ’balanced’ state can be reached; the ring state is $\left|{\Psi }_{2n}\right\rangle ={(\left|\cap \right\rangle \otimes \left|\cup \right\rangle )}^{n}$, which does not pick up any AB phase and thus causes no interference. For $N=2n+1$, the state is always un-balanced, and therefore the extra-particle can sustain AB effect. In this case, the state of the ring has the form $\left|{\Psi }_{2n+1}\right\rangle ={(\left|\cap \right\rangle \otimes \left|\cup \right\rangle )}^{n}\otimes (\left|\cap \right\rangle +{e}^{i2\pi \Phi }\left|\cup \right\rangle )$; the last part of the wavefunction reacts to flux $\Phi$ and can interfere. The resulting density pumped into the drain is shown in Fig. 5a. Incidentally, we note that a setup with two independent particle species (e.g., two internal states) can provide entangled Bell states (see the Supplementary Note 4).

Fig. 4

Pumping for interacting ring. Time evolution of topological pumping of interacting particles with ring length ${L}_{\text{R}}=6$, interaction $U/J=1$, driving frequency $\Omega =0.01J$ and potential strength ${P}_{0}=40{J}$ in band −1. a, b Density against time and sites for $N=3$ particles, a flux $\Phi =0$ and b $\Phi =1/2$. Site 0: source, site 1–6: ring, site 7: drain c, d density in source and drain for particle numbers c $N=3$, d $N=4$. In interacting system, partial transmission and reflection occurs: For this band −1 and $\Phi =1/2$, $N-1$ particles are transmitted and 1 reflected

Fig. 5

Transmission for top and bottom band. Density pumped into the drain against flux $\Phi$ for a band −1, ${U}={0.5}$, b band +1 $U = 0.1.$ a Band −1: $\Phi$ dependence changes with even/odd parity of particle number $N$. b Band +1: pumped entangled states show flux periodicity ${\Phi }_{0}\propto 1/N$ in the transmitted density. Drain density measured at time $tJ=1260$. Pumping with driving frequency $\Omega =0.01J$, ring length ${L}_{\text{R}}=8$, and potential strength ${P}_{0}=60J$

Upper band +1

This band can create highly entangled states. We choose ${\phi }_{0}=0$ so that the avoided crossing is approached from above. The density transmitted to the drain is shown in Fig. 5b. In this case, we find that tunneling between neighboring sites occurs via effective tunneling between nearly resonant states that are not connected directly via the hopping term. Here, the transitions happens via intermediate off-resonant processes. (e.g., for $N=3$ and $\left|{N}_{j}{N}_{j+1}\right\rangle$ denoting particles at neighboring sites $j$: when states $\left|30\right\rangle$ and $\left|03\right\rangle$ become resonant, they are off-resonantly coupled via the weakly occupied states $\left|21\right\rangle$ and $\left|12\right\rangle$). The effective coupling between the final states can be calculated with the Schrieffer-Wolff transformation using above reasoning¹¹. Then, the energy gap between the bands is $\Delta E\propto {J}^{N}/{U}^{N-1}$ (ref. ⁴⁷, also see Supplementary Note 1). The gap decreases sharply with increasing interaction $U$. Thus, the pumping is most efficient in the regime ${\vert} {U} {\vert} < {J}$, however the interaction should large enough $|{U}|\, {> } \, \Omega$ such that the many-body effects appear. The off-resonant tunneling process at the ring-lead interface generates NOON-like states, with a superposition state of $N$ particles being in either upper or lower part of the ring. Well defined AB oscillations are found: the AB flux quantum decreases with particle number $N$ as ${\Phi }_{0}=\frac{1}{N}$. A NOON state is a factor $N$ more sensitive to phase differences⁴⁸. Thus, the fractional flux quantum in the interference pattern is the signature for the NOON-like state in the ring. At the AB minimum, one particle is reflected, while the rest is transmitted. The dependence on driving frequency is discussed in Supplementary Note 2. The nature of the process and the fidelity of creating entangled state at the ring-lead junction is further discussed in the subsection Creating entangled states.

Central band 0^±

The dynamics for the central band depends on the choice of initial phase: We define the initial conditions ${0}^{+}$ with ${\phi }_{0}=\pi /2$ and ${0}^{-}$ with ${\phi }_{0}=-\pi /2$. The transmission depends on the ring length ${L}_{\text{R}}$ as well. For ${L}_{\text{R}}=4n+2$ and ${U}\, {> } \, 0$, band ${0}^{+}$ has the same flux dependence as the upper band +1. For ${0}^{-}$ the flux dependence is the same as the lower band −1. However, because of the different Chern number ${\mathcal{C}}=2$, in those two cases the particles move at twice the speed and in opposite direction (thus exchange $\Omega \to -\Omega$). The anti-crossing type alternates between top and bottom and the smallest energy gap that limits the dynamics scales as in band +1 ($\Delta E\propto {J}^{N}/{U}^{N-1}$).

For ${L}_{\text{R}}=4n$, the dynamics is quite different. While in the previous case, nearly all particles were transmitted, now for ${L}_{\text{R}}=4n$ the system is highly reflective and we find that maximally one of $N$ incoming particles is transmitted. For the band ${0}^{+}$ (Fig. 6a) the AB flux quantum is ${\Phi }_{0}=1/N$, revealing the NOON-like state in the ring. The transmission is much lower and parity dependent: for even $N$ and zero flux, zero particles are transmitted, while for half flux quantum one particle is transmitted. For odd $N$, we find the opposite behavior: one particle transmitted at zero flux, and zero transmitted at half flux-quantum. For band ${0}^{-}$ (Fig. 6b), the flux quantum is ${\Phi }_{0}=1$. For even $N$, the transmission is zero, while for odd $N$ it changes from one to zero with flux. The dependence on ${L}_{\text{R}}$ comes from the switch between top and bottom approaches through anti-crossings at every other site: For ${L}_{\text{R}}=4n$, the transitions at source-ring and ring-drain approach the avoided crossing from opposite ways; as the type of transition (resonant or off resonant) depends on the path in the anti-crossing, this feature implies the change in transmission behavior. For ${L}_{\text{R}}=4n+2$, instead, the transitions at source-ring and ring-drain approach the avoided crossing the same way; this features implies that the transmission is similar to what found for the band $\pm \!1$. The dependence on ${\phi }_{0}$ results also from switch between top and bottom approaches through anti-crossings: For ${\phi }_{0}=\pi /2$, the lead-ring junction is approached via the top path (off-resonant, NOON states), while for ${\phi }_{0}=-\pi /2$ via the bottom path (resonant). In our numerical simulation, we see a finite probability of reaching the drain for even number of particles due to non-adiabatic transitions. The dependence on interaction is discussed in Supplementary Note 3.

Fig. 6

Transmission for central band. Density pumped into the drain for central band $0$ against flux for $U\,\,> \,\,0$. a Band ${0}^{+}$ (${\phi }_{0}=\pi /2$): entangled state created by pumping results in fractional flux quantum ${\Phi }_{0}\propto 1/N$. b Band ${0}^{-}$ (${\phi }_{0}=-\pi /2$). Drain density measured at time $tJ=630$. Pumping with driving frequency $\Omega =-0.01J$, ring length ${L}_{\text{R}}=8$ and potential strength ${P}_{0}=60J$

Creating entangled states

In this section we highlight how to create highly entangled states of NOON-type with our proposed setup. The crucial part to create entanglement is the source-ring junction, where one input site is connected to two output sites via tunneling. This part represents a non-linear beam-splitter. To further understand the mechanism, we first look at a reduced system, where we remove all other sites of the ring-lead setup except this junction. We initialize the particles at the input site, and evolve the system. Depending on ${\phi }_{0}$ of the potential, the state after the pumping can be highly entangled. To create entangled states, we set the initial potential phase ${\phi }_{0}=0$ so that the system follows top curve of anti-crossing. The dynamics of this level is characterized by off-resonant coupling: the tunneling to the two neighboring sites is mediated by off-resonant energy levels as we explained in the subsection Upper band. Starting from the initial many-body state (for $N$ particles $\left|{\Psi }_{\text{ini}}\right\rangle =\left|N\right\rangle \otimes \left|00\right\rangle$) the state is transformed directly to the final entangled state ($\left|{\Psi }_{\text{NOON}}\right\rangle =\frac{1}{\sqrt{2}}\left|0\right\rangle \otimes (\left|N0\right\rangle +\left|0N\right\rangle )$). We plot the fidelity $F={\left|\langle {\Psi }_{\text{NOON}}| \Psi \rangle \right|}^{2}$ of the creation of the NOON like entangled state by adiabatically changing the potential in the ring-lead junction in Fig. 7. We observe that for our parameters a NOON state of up to 6 particles with nearly unit fidelity can be created. For more particles or higher interaction the fidelity decreases due to the exponential suppression of the energy gap.

Fig. 7

Fidelity for NOON-state generation. Fidelity of creating a NOON-like entangled state after pumping through a simplified ring-lead junction. It consists of three lattice sites, with one site connected to the other two sites. All particles are initialized on the first site, the NOON state is measured between the other two sites. Fidelity is plotted against interaction $U$ in units of inter-site hopping $J$. Pumping with driving frequency $\Omega =0.01J$ and potential strength ${P}_{0}=40J$

In the other case, where the particles follow the lower band of the anti-crossing with ${\phi }_{0}=\pi$, different types of states can be created. The tunneling from one site to the next occurs via resonant tunneling between the intermediate many-body states. Particles tunnel one after the other over to the neighboring sites when the states are brought into resonance by the driving. For $N=2$, the initial state $\left|2\right\rangle \otimes \left|00\right\rangle$ transforms to final state $\left|0\right\rangle \otimes \left|11\right\rangle$ via resonantly occupying the intermediate states $\left|1\right\rangle \otimes (\left|10\right\rangle +\left|01\right\rangle )$.] Driving this setup with two species of interacting particles (e.g. spin up and down) with an initial state $\left|{\Psi }_{0}\right\rangle=\left|\uparrow \downarrow \right\rangle \otimes \left|00\right\rangle$, a Bell state can be created: $\left|{\Psi }_{\text{Bell}}\right\rangle \propto \left|0\right\rangle \otimes (\left|\uparrow \right\rangle \left| \downarrow \right\rangle +\left|\downarrow \right\rangle\left| \uparrow \right\rangle )$ (see also Supplementary Note 4).

Discussion

We studied topological pumping in an interacting ring-lead system pierced by a synthetic magnetic field. Due to the interplay between topological bands and AB phase we find that the transport is substantially affected by entanglement and interaction.

Interaction fundamentally influences the topological pumping, giving each band distinct dynamics and characteristics: The lowest band has the largest energy gap. The central band either transmits or reflects nearly all incoming particles depending on the parity of the ring length. The top band creates highly entangled states.

Entanglement is generated because the ring-lead interface effectively acts as a nonlinear (Bose–Hubbard interaction) beam splitter. The oscillations of the particle transmission then occurs with a specific periodicity due to the AB interferometer. Such phenomenon traces back to the entangled nature (NOON-type) of the states involved in the transport, thus forming a fractional flux quantum. This effect may be used for quantum-enhanced interferometers with a sensitivity $\propto 1/N$. We note that the state is prepared adiabatically. Adiabatic shortcuts could reduce their preparation time⁴⁹. In addition, these entangled states are limited by an energy gap that scales exponentially with the number of particles $N$. This process is distinct from the Hong-Ou-Mandel effect which is based on two-photon interference⁵⁰. We note that in the lowest band, the energy gap scales as $\Delta E\propto \sqrt{N}$, but the state involved in the transport is not of NOON-type.

Disorder at the ring-lead interface can create a (random) particle imbalance as well as a phase shift between particles in the upper and lower part of the ring. When disorder is applied away from the ring-lead interface small disorder (compared with the energy gap) is expected not to harm the pumping protocol. We believe that a separate study should be carried out to analyse this problem.

Our setup is of direct experimental interest for various platforms of quantum technologies. For cold atom systems, specifically, decoherence is well controlled as well as smooth traps can be engineered to limit disorder^25,51,52. Interacting photons in non-linear superconducting resonators can realize topological pumping of interacting photons¹¹ and synthetic magnetic fields⁴⁴. Photonic waveguides could realize flexible designs of topological pumping¹⁰ and artificial magnetic fields⁵³, while interaction between photons can be engineered via strong coupling⁵⁴.

Methods

The equations of motions of the system are solved with exact diagonalization, by evolving the Schrödinger equation in time $\left|\Psi (t)\right\rangle ={e}^{-i{\mathcal{H}}t}\left|\Psi (0)\right\rangle$.

Transmission and reflection coefficients are derived by evaluating the dynamics of the pumped eigenstates of the reduced system: We consider only the bare junction, consisting only of three sites: one input site, and two output sites. To get the transmission and reflections coefficients, the dynamics of source and drain junction are considered.