Studying belief systems

A reinvigorated interest in attitudes and the need for adequate methodologies

Researching attitudes is a central goal of the social sciences as it can inform a wide range of pressing social phenomena (Lüders et al. 2023). Not only do attitudes reflect internal representations of the outer world; but they also permit individuals to strategically interact with their social environment as they often convey information about latent concepts such as worldviews and identities (Quayle, 2020; Klein et al. 2007). For instance, when navigating social contexts that are less explicit or clearly defined, such as social media, individuals rely on meaningful cues to evaluate and categorize their social environment (Postmes et al. 2005), and there is good reason to believe that attitude expressions in the form of tweets, likes, hashtags, user-bios, and other available affordances serve exactly such functions (Lüders et al. 2022; McGarty et al. 2014). Hence, by engaging with other users through attitude expressions, individuals strategically locate themselves within their wider social environment. Conversely, by using attitudes as social cues, individuals can infer information and make judgements about others (Lüders et al. 2022).

Network-based methods provide novel opportunities to study the structural basis of complex attitude systems, therefore helping researchers reassessing their meaning for abstract concepts like worldviews, identities, and ideologies. Furthermore, by operationalizing attitudes at the system level, attitude networks can foster the understanding of social influence and attitude change (Carpentras et al. 2022). These advantages hold theoretical as well as practical value. For instance, the research found that shared attitude (dis)agreement lies at the core of group constructions among climate change advocates and sceptics (Bliuc et al. 2015) and that newly emerging belief networks in the wake of the Covid-19 pandemic successfully predicted health measure compliance (Maher et al. 2020).

Belief Network Analysis for studying attitude systems

Belief network analysis (BNA) is a relatively young approach for exploring concepts such as attitudes, goals, or values as well as their mutual interplay. In this paper, we loosely use the term to refer to the family of approaches that treat beliefs (or attitudes, opinions, etc.) as nodes and build links between them using linear correlation (e.g. Converse, 1964; Boutyline and Vaisey, 2017). Belief networks thus differ from network methods that represent people as nodes (e.g. retweet networks, follower networks). While social network methods usually try to provide a structure of the social connections among the studied population, belief networks provide information about the structural organization of belief systems (Boutyline and Vaisey, 2017; DellaPosta, 2020; Brandt et al. 2019; Kertzer et al. 2019). Since BNA are network-based methods, they allow for quick visual inspections of belief systems, as well as precise and quantitative analysis of their underlying attitudinal architecture.

Even though some BNA techniques can be applied to diverse types of data (e.g. unstructured data from social media), they are usually used to process survey data, modelling items as nodes while edges are derived from some form of inter-item correlation (Boutyline and Vaisey, 2017; DellaPosta, 2020; Brandt et al. 2019; Kertzer et al. 2019). The process for producing a network is typically simpler than the steps required for many other techniques extracting structural features of multidimensional relationships between items. For example, common techniques such as factor analysis aim to summarize a larger set of items into a smaller set of factors. In contrast, BNA outlines a “map” of relationships between items, however, without changing their qualitative interpretationFootnote 1. To achieve this, BNA methods simply calculate the strength of between-item relationships for each pair of items and incorporate this information in the network as each link’s weight. This weight is usually calculated as a correlation (Boutyline and Vaisey, 2017), although many alternatives are possible, such as the Kullback-Leibler distance (Kertzer et al. 2019).

Belief networks that are obtained in such ways can be visually inspected based on standard visualization techniques from network analysis (Krempel, 2011). This initial step offers a quick and intuitive (but imprecise) way to explore the structures of belief networks. Visual inspection can be used to identify clusters (DellaPosta, 2020), peripheral nodes, and positive or negative relationships between items (Boutyline and Vaisey, 2017; Brandt et al. 2019), or used to (roughly) estimate the number of factors in the dataset and their relationship to each other (Kan et al. 2020).

A more precise analysis of belief networks can be realized based on quantitative techniques developed in network analysis (Serrat, 2017). For example, it is possible to estimate the size of a cluster (i.e. how many nodes compose it), how separate it is from the rest of the network, which are the most central nodes, etc. (Boutyline and Vaisey, 2017; DellaPosta, 2020; Serrat, 2017). Indeed, it is common practice to start with a visual and qualitative inspection of a network and then analyze its properties more deeply based on quantitative techniques.

Another major advantage of BNA is that despite being a network-based method, BNA is computationally fast, hence allowing the analysis of large datasets. Indeed, in many network-based methods the time required for the calculation grows non-linearly with the number of nodes (Wakita and Tsurumi, 2007). This means that several techniques that model people as nodes cannot be applied on big datasets, as they will require excessive computational time. Conversely, modelling items as nodes allows for a more parsimonious network structure and hence more computational resources.

Limitations of belief network analysis

While BNA has been proven to be a very powerful and promising tool, like any other method, it also suffers from various limitations. The first stems from the techniques that are used for calculating the weights of links that connect two nodes. As previously mentioned, link weights are typically calculated based on linear correlation (Boutyline and Vaisey, 2017). However, these methods can only reflect monotonic (i.e. only increasing or only decreasing) relationships (De Winter et al. 2016). Let us consider a practical example in which survey participants from both extremes of the political spectrum (i.e. left, right) score high on a fictitious “item 1.” Let us also suppose that moderates (i.e. people falling between the two poles) score lower on that same item. The data resulting from this example would follow a U-shaped curve (Fig. 1a). Despite the fact that this relation is characterized by very low random fluctuations (i.e. based on one variable one can precisely predict the other), the calculated correlation coefficient would be zero. Thus, by looking only at the correlation value, most people will erroneously conclude that no relationship exists between item 1 and the left-right spectrum.

Fig. 1: Simulations of possible different response patterns.
figure 1

a Despite having no random variations in the relationship, the correlation between the two variables is zero. b–d Three very different relationships producing the same correlation (r = 0.45).

Full size image

The simulated relationships depicted in Fig. 1b–d reveal a different problem as very different relationships produce the same correlation value (r = 0.45). Figure 1b, c show the case in which all people score the same value except for people on the extreme left (1b) or the extreme right (1c). Therefore, these two items characterize very precisely those people who are falling at the extremes of the spectrum. Instead, Fig. 1d shows a more classical linear relationship between variables but with much higher uncertainty (i.e. we cannot precisely infer one variable’s value from the other, due to random fluctuations). Unfortunately, just by looking at the link between two nodes (i.e. the information provided by BNA), we will not be able to understand which of these three patterns is producing the calculated correlation value.

Some alternative methods have been suggested to address such problems. For example, instead of using correlation to estimate link weights, some authors used the Kullback-Leiber distance (Kertzer et al. 2019). However, this does not solve the problem that different curves will result in the same coefficient (thus, being indistinguishable during the network analysis phase). Indeed, this ambiguity does not stem from the use of a specific correlation or distance, but from the fact that we are trying to summarize the relationship between two variables with a single number. Furthermore, the use of less known measurements may increase the difficulty of interpreting results, as many researchers would not be familiar with their meaning.

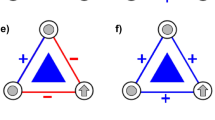
The use of these metrics to summarize relationships also has some important consequences for the interpretation of latent constructs such as group identities. For example, let us suppose we run our analysis on 4 political items, including one item that assessed peoples’ self-placement on a left-right continuum. Let us further assume that these procedures would provide a network like the “original network” shown in Fig. 2a. The results would lead us to the following conclusion: as we move towards the left side of the spectrum, respondents tend to answer more positively to both item B and item C (we infer this from the positive correlation between B and C with the left-right self-placement item “LR”). Conversely, as we move towards the political right, people become more and more negative towards items B and C. We would further conclude that item D has no connection to political self-identification (i.e. item D has negligible correlations with the other items).

Fig. 2: Exploration of response patterns using BNA.
figure 2

a Interpretation of a network from BNA. b Example of an asymmetric relationship. People on the extreme right have a clear attitude stance, whereas people on the extreme left do not.

Full size image

As the reader may notice, this interpretation implicitly assumes that the attitudes held by people on the extreme left and right are symmetric: the more positive left-wingers are towards an item (e.g. a certain policy) the more negative are right-wingers, and vice versa. However, the relationship may be more complex, and some links may exist for only one ideological side but not the other. Indeed, right-wingers may be positive towards a particular topic (e.g. country music), whereas left-wingers may have no defined opinion on the topic (i.e. some left-wingers may like it, some may dislike it and some others may be neutral). An extreme case of this is represented as an example in Fig. 2b. While the interpretation of the correlation would be technically true that “the prototypical right-winger, on average, likes country music more than the prototypical left-winger,” it would still hide the information that “right-wingers, in general, tend to have a clear liking for country music, while left-wingers, in general, do not have a clear preference.”

Of course, many of these problems could be solved by manually inspecting the relationship between pairs of items (i.e. their scatterplot). However, the number of relationships to explore is roughly \({N}^{2}/2\) where \(N\) is the number of items. This results in a very long and complex task, particularly when considering that normal relationships are usually more complex than the extreme cases that we have simulated so far. Furthermore, inspecting each inter-item relationship in isolation would still not provide a good understanding of the overall attitude system. Indeed, the promise of BNA is to show key properties of an entire attitude system within a single network (ideally, at a single glance), while putting immediate attention on similarities and differences between groups.

A belief network with a latent space

In a recent publication (Carpentras et al. 2022), we used a modified version of BNA and other methods to outline attitude dynamics in the context of vaccination. The employed BNA modifications not only offer more detailed information about participants’ vaccine-related belief system, but one parameter extracted from it allowed us to make predictions of opinion change and behavior. This parameter was also strongly connected with spatial distance in the visualization, suggesting the idea of an underlying “opinion space.” Comparably, in another manuscript (Lüders et al. 2024) we used the information about spatial locations in the visualization to predict political party identification. In the current work, we explain and validate this variation of BNA as a spatial network of attitudes (Barthélemy, 2011; O’Sullivan, 2014). In other words, the output of this new method can be thought of as a network in which each node holds a spatial coordinate in what we might call an attitude or identity space. Spatial networks have already been used in situations such as networks of airports, where it is not only important if two airports are connected by some flights, but also their position and distance in the physical space. However, as we will discuss, in our case the x-coordinate will correspond to positions in a latent space. To validate this procedure, we will develop a mathematical model to have a better understanding of how nodes are spatially located by the algorithm. Furthermore, we will compare the results that we obtain with our new method, called ResIN, with results from Item Response Theory (IRT) using both simulated and empirical data from political surveys. Furthermore, we will show how ResIN can provide “in a glance,” interesting results which are either hard or impossible to identify with the other methods. In doing so, we will demonstrate the value of ResIN for studying belief systems as well as psychological concepts like group identities.

In the next section, we will clarify how ResIN works and how it can be used to explore multiple belief systems within a single attitude space. Subsequently, we will develop a mathematical model to show how ResIN relates to IRT. Finally, we will validate ResIN using simulated and real-world data.

Introducing ResIN

As previously discussed, BNA usually considers items as nodes and their correlation as the link’s weight. ResIN instead, similarly to item-response theory, focuses on item-responses, and consequently models item responses as nodes. For instance, if an item “vaccines are useful” has five levels, ranging from “Strongly agree” to “Strongly disagree,” ResIN will produce 5 different nodes, each reflecting a different response option (e.g. “Vaccines are useful: Strongly agree”, “Vaccines are useful: Somewhat agree”, etc.). When dealing with a dataset, this approach can be done through a process called “dummy coding.” This operation can be described as producing multiple binary variables from a single variable (Jose, 2013). Keeping the previous example, we would obtain a binary variable for each response option (e.g. “Vaccines are useful: Strongly agree”) whose values would be 1 for every person selecting this item-response and 0 for every person selecting a different item-response. While some readers may think of dummy coding as a redundant process, we will see that it will allow us to have a much more detailed description of the relationship between items and, consequently, allow more flexibility in the attitude system. More specifically, ResIN abandons the assumption that survey responses have interval (or even ordinal) measurement properties at the individual level, and instead, it reconstructs spatial relations at social levels.

Having defined what the nodes are, the next step is to identify how to properly weight the links. Following the common approach of BNA we calculate the weights as the correlation between the corresponding node variables. Conveniently, as we are dealing with binary variables, we do not even have to choose between Pearson’s correlation, Spearman’s correlation, or Phi correlation (which was developed for calculating the correlation of binary variables) (Guilford, 1941). Indeed, when dealing with binary variables, all of these metrics produce exactly the same result (Ekström, 2011). This is also very useful as many researchers might be familiar with one (e.g. Pearson), but struggle to interpret values from different coefficients. Note that correlations between responses of the same item (e.g. “Gun control:agree” and “Gun control:neutral”) will not be calculated. This will be further justified later while discussing negative correlations, but we can immediately notice how these responses are mutually exclusive, thus not adding information to the system. Also notice that, for two 5-levels items, ResIN will produce 25 edge-weights (the correlations between all possible between-item response pairs) while BNA will produce only one (i.e. the correlation between the two items). This will be at the core of why ResIN can analyze more complex situations such as asymmetric opinion spaces without losing information.

Up to this point, ResIN has produced an attitude network in which nodes reflect dummy coded item-responses and links reflect the correlations between different nodes. However, as we will see in the next step, ResIN also produces spatial information. Spatial networks are specific types of networks in which nodes have spatial coordinates in a (usually bi-dimensional) space. To obtain the spatial coordinates, ResIN uses a force-directed algorithm (Fruchterman and Reingold, 1991). This algorithm models every node similarly to an electrically charged particle (e.g. an electron) resulting in a repulsive force between them. This means that nodes will try to maximize their distance with respect to each other. At the same time, links act as springs pulling the connected nodes together. Specifically, the bigger the link weights, the stronger the force pulling two nodes together. As a result, groups of nodes that are strongly correlated will be positioned close to each other, while nodes that are weakly correlated with the rest will appear further apart.

One may critically notice that the force-directed algorithm allows ResIN to work only with positive edges, therefore forcing us to neglect the negative correlations for this specific step. However, as we will see when exploring the mathematical model, this will not result in a loss of precision, as negative correlations contain mostly redundant information about the attitude system. Notice also that this does not mean that the information from the negative edges is lost, but only that it is not used for determining the spatial location, while it can still be used for any other type of analysis.

An example of our method is provided in Fig. 3a, where we run the method on a simulated (i.e. “toy”) dataset. As we can see, we produced 5 items (labeled with letters from “a” to “e”), each with 5 levels (identified by different colors), for a total of 25 item-responses. Clusters (i.e. groups of nodes that appear close to each other) in this figure represent patterns of item-responses which are frequently selected together by (simulated) participants. For example, participants who selected one of the red responses are also very likely to select the other red responses (we see this from their spatial proximity). We can also tell that a participant selecting a red response will probably select a yellow response (from the high number of red-yellow links and their spatial proximity) but not a grey or blue response (from the relative lack of links and further distance to the red cluster).

Fig. 3: ResIN and BNA visualization of a simulated dataset.
figure 3

a Pattern of simulated data obtained with the ResIN method and b pattern obtained from the same data with classical BNA. Letters represent different items, while colors in a represent different levels (e.g. “strongly agree”, “weakly agree”, etc).

Full size image

Notice also that all clusters have 5 nodes, besides the grey one. This means that while all five responses are important for characterizing the other clusters, only four responses characterize the grey one. For example, this might represent Democrats (blue) having a strong correlation with “liking latte” and Republicans (red) characterized by “disliking latte” (DellaPosta et al. 2015). Therefore, we might expect independents (grey) then to be characterized by a neutral item-response (e.g. they will usually select: “neither like nor dislike”). However, we decided to simulate a more realistic scenario in which some independents may like latte, others may dislike it, and others may be neutral on the topic. Therefore, we observe no strong association between independents and being neutral about latte.

The same can be understood as the possibility of guessing the coffee preference of a person just by knowing their political affiliation. While our guess would be remarkably precise for Republicans and Democrats, this would not be the case for independents. This can be easily visualized by ResIN as the cluster of independent attitudes will not include any response about coffee.

Figure 3b also depicts the pattern one would obtain using classical BNA with the same data. In contrast to the results obtained via ResIN, with classical BNA the information of independents having no clear positioning on coffee would be lost. The reason is that classical BNA produces only five nodes and 10 links, compared to the 25 nodes and roughly 100 links displayed in ResIN.

Connection to item-response theory

One of the most important concepts in item-response theory (IRT) is the so-called item characteristic curves (IC curves) (Van der Linden and Hambleton, 1997). Given a certain latent construct (e.g. left-right spectrum) and an item-response R, an IC curve \({f}_{R}(\theta )\) represents the probability that a person with value \(\theta\) of the latent construct will select R as an answer (Van der Linden and Hambleton, 1997; Thomas, 2011; Drasgow and Hulin, 1990). These curves are often characterized by several parameters such as the pseudo-guess value, the discrimination, and the difficulty value. This represents both the strength of IRT, as it allows us to finely tune items and scales, but also one of the main obstacles, resulting in a potentially overwhelming amount of information. As we demonstrated before, ResIN represents each item-response as a single node \({n}_{R}\). ResIN therefore contains less information than IRT which makes it a poor candidate for precise scale tuning, but, as we will see, dramatically improves its applicability as a network tool.

As we will show in the following, the x-coordinate of each node obtained through ResIN corresponds to the mean of the IC curve in IRT. To be able to perform calculations, we will have to make some stringent assumptions. However, in later sections, we will re-test the equivalence of ResIN and IRT using simulations that are based on more relaxed assumptions. Finally, we will validate the relationship between the two methods using empirical data.

Phi correlation and overlap

In this section, we will show that the correlation between two item-responses (i.e. the weight of the link) provides information on “how close” two IC curves are (we will formally define the concept of “closeness” in a few lines). Firstly, we can start by using the formula of the \(\phi\) correlation coefficient for two columns \({x}_{1}\) and \({x}_{2}\) in a dataset as (Guilford, 1941):

$$\phi \left({x}_{1},{x}_{2}\right)=\frac{{n}_{11}{n}_{00}-{n}_{10}{n}_{01}}{\sqrt{{n}_{1{{\bullet }}}{n}_{0{{\bullet }}}{n}_{{{\bullet }}1}{n}_{{{\bullet }}0}}}$$
(1)

Where \({n}_{{yz}}\) is the number of rows in which column \({x}_{1}=y\) and column \({x}_{2}=z\). When one of the two entries is labeled with a dot, as in \({n}_{y\bullet }\) it means that that variable may be either 1 or 0. So \({n}_{1\bullet }\) is counting only the number of rows in which \({x}_{1}=1\) independently of the value of \({x}_{2}\).

To connect this formula to IRT, we can rewrite each one of the \({n}_{{yz}}\) variables as function of the IC curves. For example, for a uniform population \({n}_{1\bullet }\) can be written as:

$${n}_{1{\bullet }}=\int {f}_{1}\left(\theta \right)d\theta$$
(2)

Because of this, we rewrite ϕ as:

$$\phi =\frac{I-{b}_{1}{b}_{2}}{\sqrt{{b}_{1}{b}_{2}(1-{b}_{1})(1-{b}_{2})}}$$
(3)

Where I is the overlap of the two functions, defined as:

$$I=\int {f}_{1}\left(\theta \right){f}_{2}\left(\theta \right)d\theta$$
(4)

And bi is the area of the IC curve i, written as:

$${b}_{i}=\int {f}_{i}\left(\theta \right)d\theta$$
(5)

Something that can be noticed from Eq. (3) is that \(\phi\) is linearly dependent on the overlap \(I\). Therefore, the bigger the overlap between the two curves, the bigger the correlation value \(\phi\) will be.

Until now, we have not specified anything about the IC curves. Indeed, different theories from IRT use a different family of curves, even if, in many cases, they are similar to Gaussian-like functions. Therefore, for now, we will consider the curves to be Gaussian, obtaining the following overlap (Bromiley, 2003):

$$I={K}_{1}{e}^{-\frac{{\Delta }^{2}}{{K}_{2}}}$$
(6)

Where \(\Delta\) is the distance between the two curves calculated as the difference between their mean (i.e. \({\mu }_{1}-{\mu }_{2}\)) and \({K}_{1}\) and \({K}_{2}\) depends only on \({\sigma }_{1}\) and \({\sigma }_{2}\).

To make this clearer, in Fig. 4 we plotted the correlation values (using Eq. 3) depending on the overlap \(I\) and the distance \(\Delta\) of two gaussian IC curves. As expected from the formulas, as the overlap between the curves increases, the correlation increases linearly (Fig. 4a). Furthermore, the relationship between the correlation and the distance between the curves (Fig. 4b) is monotonic though not linear. Meaning that the slope becomes smaller with increasing distance (i.e. flattening of the curve). The practical consequence of this is, that for positive correlations, \(\phi\) is a good measurement of the curves’ distance (being roughly linear). However, for negative correlations, it progressively loses sensitivity (i.e. the derivative becomes smaller). Therefore, by dropping the negative correlations (as discussed in section 2) we are losing very little information about the distance of the curves.

Fig. 4: Correlation between items as function of item’s overlap and distance.
figure 4

a Relationship between correlation and the overlap of two curves. b Correlation vs curves’ distance for Gaussian curves. Blue (dark grey) points represent correlation values below zero, while red (light grey) points represent positive correlation.

Full size image

Alternatively, this could be also understood by imaging varying the distance \(\Delta\) between two curves and observing how this affects the correlation value. For positive correlations, this relationship will be linear. For instance, moving from \(\Delta =1\) to \(\Delta =1.5\) the correlation will decrease by 0.2, and similarly if we move from 1.5 to 2.0. Thus, a shift of 0.5 will roughly decrease the correlation by 0.2. However, when the correlation is below 0, especially for \(\Delta\) bigger than 3, the relationship between the two variables changes. Indeed, moving from 3 to 5, which is 4 times bigger than previous shifts, will cause a decrease in correlation slightly bigger than 0.1. Indeed, we can observe that close to 5 the curve is extremely flat.

Practically this means that when curves are “close” (i.e. having positive correlation) we can “observe” differences in position by observing differences in the correlation value. However, this information is progressively lost as the correlation becomes more negative. Indeed, a correlation of −0.35 may represent a distance of 5 as well as 7. This means that for negative correlations the process of estimating the spatial positioning from the correlation value becomes rather unreliable.

Forced-directed method and position

As previously outlined, to obtain the final attitude space, we use a force-directed method to estimate the position of each node. In such a configuration, each node experiences an attractive and a repulsive force following the formulas (Fruchterman and Reingold, 1991):

$$\begin{array}{c}{F}_{a}\left(d\right)=w\frac{{d}^{2}}{{k}_{1}}\\ {F}_{r}\left(d\right)=-\frac{{k}_{2}^{2}}{d}\end{array}$$
(7)

Where \({k}_{1}\) and \({k}_{2}\) are two constants, \(w\) is the link’s weight and \(d\) is the distance between the two nodes. In order to find the position of an item response, we need to find the equilibrium of the dynamic system as:

$$\sum {F}_{i}\left(\theta \right)=0$$
(8)

A non-approximated solution will be provided in the next section, where we will run ResIN with simulated data. Here, to provide more insight, we consider the special case in which all nodes but one are fixed at the coordinate of the mean of the corresponding IC curve (i.e. \({\theta }_{i}={\mu }_{i}\)). Then, by supposing only attractive forces, and approximating the correlation as proportional to the curve’s mean distance (as in Fig. 4b), we will test whether the last node j will also be placed at the “correct” x-coordinate (i.e. \({\mu }_{j}\)).

Therefore, to find the position \({\theta }_{j,{fin}}\) of the node at the equilibrium, we must solve the system:

$$F\left({\theta }_{j,{fin}}\right)={\mathop{\sum}\limits_{i}\frac{{\phi }_{{ij}}}{{k}_{1}}}{\left({\theta }_{j,{fin}}-{\mu }_{i}\right)}^{2}=\frac{{k}_{3}}{{k}_{1}}{\mathop{\sum}\limits _{i}}{\left|{\mu }_{j}-{\mu }_{i}\right|\left({\theta }_{j,{fin}}-{\mu }_{i}\right)}^{2}=0$$
(9)

Where \({k}_{3}\) is the constant of proportionality between \(\phi\) and the difference of the means \(|{\mu }_{j}-{\mu }_{i}|\).

We solved this equation numerically for different positions of the means. We randomly assigned all the \(\mu\) values (including \({\mu }_{j}\)) using a uniform distribution. Then we numerically found the \({\theta }_{j,{fin}}\) which minimizes the absolute value of the force calculated using Eq. 9. We repeated this process for 1,000 configurations (every time randomizing all the μ values). As depicted in Fig. 5, \({\theta }_{j,{fin}}\) is proportional to \({\mu }_{j}\) for all the tested points. Indeed, we can also calculate the correlation coefficient between the two, finding r = 0.994. This suggests that by using \(\phi\) as the link’s weight, the force-directed algorithm should place the nodes close to the mean value of the corresponding IC curve; at least, in this very simplified condition.

Fig. 5: IC curves’ mean versus position estimated by the force-directed method.
figure 5

We can notice how the relationship between the two variables is monotonic and almost linear, besides the extremes where some compression is present.

Full size image

Something that we can notice is that Fig. 5 presents some form of “compression”, where the interval [0,1] is mapped into the interval [0.2, 0.8]. This is due to the fact that we have neglected the repulsive forces. Indeed, this approximation works particularly well for nodes that are close to the center, as their position is mainly determined by how they are “pulled” by the surrounding nodes. However, the position of the nodes at the periphery is determined by the attractive and the repulsive forces as they will experience no pull on one side. Notice, however, that this will not be true for the full method, as it will include both attractive and repulsive forces.

Simulations

In the previous sections, we have showed (using very stringent assumptions) that the position of the nodes in ResIN is proportional to the position of the IC curves in item response theory (IRT). Here, we will strongly relax the previous assumptions and test the entire system all at once using simulated data, showing an even more robust relationship between the two. We hereby follow the below procedure:

  1. 1.

    We generated a series of curves using the graded model from IRT (Samejima, 1969; Samejima, 2010).

  2. 2.

    We calculated the correlation among item-responses by using Eq. 3 (i.e. from their IC curves) for a normally distributed population, thus obtaining the network.

  3. 3.

    We use the force-directed method from the Python Networkx package to estimate the position of the nodes in the opinion space.

  4. 4.

    We use principal component analysis (Jollife and Cadima, 2016) to rotate the opinion space in such a way that the main axis along which nodes are distributed will coincide with the x-axis.

  5. 5.

    We compare the x-coordinate of each node with the mean of the corresponding IC curve from IRT.

Notice that, while many models in IRT suppose quite simple curves (e.g. all the same amplitude) (Van der Linden and Hambleton, 1997), the graded model allows for a lot of variation between curves. For example, in Fig. 6a we can see the 5 curves for the 5 response-options of a single simulated item. It is possible to see that IC curves vary in terms of amplitude, standard deviation, and even shape. This completely relaxes the stringent requirements we imposed in previous steps to be able to mathematically explore the relationship between the two methods. Therefore, the graded model allows for a test in much more complex (and realistic) situations.

Fig. 6: Correspondance between ResIN and IRT for simulated data.
figure 6

a An example of the IC curves used for simulating one of the items. Notice how curves have different amplitudes, standard deviations, and even shapes. b Position estimated by the ResIN method versus the mean of the corresponding IC curve for the case of 8 items and 5 levels.

Full size image

In Table 1 we reported different values of Pearson’s correlation between the position estimated by the ResIN method and the mean value of the corresponding IC curve. For each configuration, we obtained a correlation coefficient of r ~ 0.95, meaning that the position obtained from the ResIN method approximates very well the position of the curves from IRT.

Table 1 Correlation between the nodes and the mean of the corresponding IC curve.
Full size table

Analysis of empirical data

In the previous section, we tested our method against simulated data which were obtained from item-response theory. This was instructive, as it allowed us to have a ground truth for checking if the results were consistent with what we expected under different conditions. For a final validation, we will test whether we can replicate this relationship with empirical data. In doing so, we will also show that the ResIN method can produce interesting insights that would not be visible by inspecting the data with classical belief network analysis (BNA) and IRT.

Data collection and pre-processing

To perform this analysis, we collected data from N = 402 Americans (Age: 18–81, M = 34.0, SD = 11.6 Gender: male 203, female 196, non-binary 3) through the crowd working platform Prolific Academic. Participants answered 8 items on political issues (Malka et al. 2014). Each item had 5 levels ranging from 1 = Strongly agree to 5 = Strongly disagree. We then used these data to produce 8*5 = 40 item-responses, calculated their correlations, and, finally, we used the force-directed method to produce the attitude network shown in Fig. 7. The items were as follows:

  1. 1.

    Abortion should be illegal.

  2. 2.

    The government should take steps to make incomes more equal.

  3. 3.

    All unauthorized immigrants should be sent back to their home country.

  4. 4.

    The federal budget for welfare programs should be increased.

  5. 5.

    Lesbian, gay, and trans couples should be allowed to legally marry.

  6. 6.

    The government should regulate businesses to protect the environment.

  7. 7.

    The federal government should make it more difficult to buy a gun.

  8. 8.

    The federal government should make a concerted effort to improve social and economic conditions for African Americans

Fig. 7: Comparison between ResIN, IRT and BNA on empirical data.
figure 7

a Attitude network obtained by running the ResIN method on the data. Color has been used to identify different levels. b Relationship between nodes position and the mean of the equivalent IC curve from IRT analysis. c Network obtained using classical BNA on the same dataset.

Full size image

Of these 8 items, 6 were written in such a way that the answer “Strongly agree” was more associated with a Democrat position and “Strongly disagree” with a Republican position. The remaining 2 items instead were inversely coded to prevent respondents from simply providing the same answer to all 8 items. After data collection, we inverted those two items, to obtain consistent patterns. i.e. level 1 is the most conventionally Republican response and level 5 is the most Democrat response for every item. Notice that this is not needed for the main algorithm, but it is done only to make visualization 7a clearer, as we use colors to visualize levels of agreement as follows: dark blue is used for dominantly Democrat-associated item-responses (level 1; strongly agree) and red for dominantly Republican-associated item-responses (level 5; strongly disagree). Pale blue, grey, and orange are respectively levels 2 (weakly agree), 3 (neutral), and 4 (weakly disagree). If we did not reverse code the two items, their positions would still be the same, but the colors would be inverted (e.g. red for level 1).

We also collected information about self-identification as Republican or Democrat. Also in this case, we did not use this information to obtain Fig. 7a, but only to confirm that its division into Republican and Democrat was consistent with self-identification, as we will explain in the next section.

Data analysis and insights

To confirm the relationship between ResIN and IRT we extracted the position of nodes using the ResIN method in Python. To calculate the mean values of the IC curves, we followed a completely independent approach. This was done to guarantee the independence of the two results that we intend to compare. For the IRT analysis, we fed the data into the graded model (Samejima, 1969; Samejima, 2010) from the ltm package in R (Baker and Kim, 2004; Rizopoulos, 2007), from which we extracted the IC curve parameters and means. Finally, we correlated the means of the curves with the nodes’ positions. This resulted in a correlation value of r = 0.97 (p < 10−27). The relationship between the two results can be observed in Fig. 7b. This confirms that the x-axis position of nodes in the ResIN network maps very well to the mean of the corresponding IC curves in the used dataset. This observation confirms our assumptions that the understanding of spatial distance in ResIN (on the x-axis) can be interpreted as a distance on a latent variable.

Now that the connection with a well-established theory (i.e. IRT) has been demonstrated, we can analyze Fig. 7a to see if it provides some useful insights. From visual exploration, we can already notice that nodes of the same color (i.e. same levels on the left-right spectrum) are placed close to each other within the network. This observation is another confirmation that ResIN is “behaving” as expected, namely, that a person who selects a specific item response (e.g. the most prototypical Republican response to item x) would select related responses across other items as well.

Another confirmation that ResIN is working as expected is the fact that the blue cluster and the red cluster (i.e. the two most ideologically extreme) are placed at the two extremes of the attitude space. Indeed, since ResIN produces results comparable to IRT, we expect the pattern to be based on the left-right spectrum.

A surprising result comes from the fragmentation that can be observed in the middle of Fig. 7a, where the system seems to be split into two major clusters: one including the dark blue and part of the pale blue, and another bigger cluster including all the rest. This visual cue can be confirmed by running Gephi’s modularity algorithm (Lambiotte et al. 2008), based on the Louvain method (Blondel et al. 2008) which also identifies two main clusters. Nodes from the two clusters are colored respectively in orange and violet in Fig. 8a.

Fig. 8: Analysis of the clusters obtained from empirical data.
figure 8

Coloring of the graph based on a clusters identified by Gephi’s modularity algorithm and b self-identification (blue=democrats, red=republican).

Full size image

Since the links in our algorithm represent positive correlations, we can interpret each cluster as a response pattern which is common in the population. For example, people selecting one of the responses of the left cluster are also very likely to select their other responses from the same cluster. Furthermore, they are not very likely to select responses from the other cluster.

As this cluster contains either strongly or weakly Democrat-associated responses, it is easy to classify it as a Democrat cluster. By exclusion, the other cluster should be the one containing Republican responses. Yet, it is important to notice that the extracted Republican cluster contains also all the “neutral” responses and even three responses that could have been associated with Democrats (if one would naively follow an interval continuum in which “neutral” responses represent the qualitative midpoint, dividing Republican and Democrat opinions). Namely three of the pale blue nodes:

  • Abortion should be illegal: somewhat disagree

  • Lesbian, gay and trans couples should be allowed to legally marry: somewhat agree

  • The government should regulate businesses to protect the environment: somewhat agree

To make sure that this result is a real feature of the system and not an artifact we correlated each response with the self-identification variable (Fig. 8b). Here nodes’ color represents the self-reported political identity of participants who most often selected that node as a response. For example, nodes colored in blue are more likely to be selected by (self-identified) Democrats, while nodes in red are more likely to be selected by (self-identified) Republicans. This division replicates almost perfectly the split in the responses provided by ResIN, confirming that the split produced by our method is not an artifact, but rather, it reflects the fact that neutral as well as some moderate responses tend to be more frequently selected by Republicans than by Democrats.

In the next section, we will offer a brief explanation of why we may observe such an asymmetrical pattern. Before doing so, however, we will focus on the fact that ResIN was able to recognize this unexpected split in the data without having access to participants’ self-identification scores. Note that this information is undetectable in a network obtained from classical BNA (Fig. 7c). As depicted in Fig. 9, even if the split between the two clusters is embedded in the curves from IRT, the information density in this figure is so high that recognizing this split simply by looking at the curves is extremely challenging, if not impossible.

Fig. 9: IC curves obtained by using the analysis with the ltm package in R.
figure 9

IRT allows for a better exploration of the detail of each response-option. However, the overall amount of information does not really allow to easily identify overall patterns as done in ResIN.

Full size image

Further explanation of response-items’ positions in the attitude space

In our previous analysis we showed how responses that might naively be thought to be associated with Democrat identity, such as “Lesbian, gay and trans couples should be allowed to legally marry: somewhat agree,” are in fact more associated with Republican identity (i.e. the “somewhat agree” option was more often selected by Republicans than by Democrats). A possible explanation for this anomaly could be that having clear (i.e. extreme) stances on abortion, gay rights, and environmental protection is essential for the self-understanding (i.e. identity) of what it means to be a Democrat. The same topics might be less important for the average Republican voter which is why Republicans can hold a wider spectrum of beliefs (note however, that also for Republicans extreme responses seem to be the most prototypical).

We can understand this better by considering an example from a different context, such as the flat-Earth conspiracy theory. In this case, when presented with an attitude measure such as “the Earth is not flat”, most people will select the most extreme option (e.g. Strongly agree). Instead, people who are more connected to “alternative truths” (e.g. the Earth is flat, the Earth is a hologram, etc.) would be much more likely to select options such as “neutral” or “somewhat agree.” Put differently, showing any doubt at all would position you outside the mainstream. Therefore, on a 5-level item, the pattern of answers will not be “2 levels which are selected by flat-earthers, 1 level selected by neutrals, and 2 levels selected by non-flat-earthers.” Instead, it would be: “4 levels selected by flat-earthers and 1 level selected by the non-flat-Earthers.” A similar pattern is also observed in vaccine hesitancy (see Carpentras et al. 2022 for an extended analysis).

Further validation

Despite the robust relationship between ResIN and IRT, skepticism may result from relying on the force-directed algorithm as, in the literature, it is mainly used for visualization purposes. However, it is crucial to notice that even if a tool has been mostly used for a specific purpose, it may still produce excellent results also in other contexts. A famous example is the telescope, which was initially developed for terrestrial purposes (i.e. looking at far objects, like ships) but then it became a fundamental tool for the study of celestial objects. More recently, Ising’s models of atomic magnetic interaction have been applied to the study of social influence (Ising, 1925) and even as a basis for network psychometrics (Dalege et al. 2017). In a similar fashion, it is not impossible for an algorithm mimicking physical forces (i.e. the force-directed algorithm) to produce results comparable to an established psychometric theory (IRT).

In previous sections, we have already shown how the force-directed model can produce high-quality results which are extremely close to the ones from IRT (i.e. via mathematical modelling, simulations, and real data). Here we want to compare this methodology with another popular approach: multidimensional scaling (MDS).

In Fig. 10a, b we compare the 2D visualization of multidimensional scaling and ResIN for the same data simulated from the graded model (following the same procedure as section “Simulations”) having 8 items, each with 5 levels. MDS was calculated using the function MDS from sklearn.manifold in python.

Fig. 10: Comparison between ResIN and MDS.
figure 10

a Placing the nodes in the 2-dimensional space according to MDS. Notice how the structure is curved, suggesting a second dimension even if IRT has used only 1. b The same data visualized with ResIN showing no curvature. c Scatterplot of the relationship between ResIN (blue) and MDS (orange) compared to IRT. d Scatterplot showing the position of the nodes in ResIN when re-running the force-directed algorithm. Closeness to the diagonal shows very minimal variations.

Full size image

The first thing we can notice is that, obviously, classical MDS is missing the network structure, even if this could be solved by simply combining the information from the two methods. The second noticeable result is that, even if the simulated data are unidimensional, the visualization of MDS is curved, almost introducing an artificial second dimension. While this effect may be surprising to some, it can be explained by the fact that IRT and MDS are different methods operationalizing dimensions in different ways. Therefore, what is unidimensional in IRT can correspond to multiple dimensions in other methodologies. Despite this, it is interesting to notice how in ResIN the network mainly follows a unidimensional structure.

Another interesting comparison is which of the two methods (ResIN and MDS) produces results on the main axis which are closer to IRT. Figure 10c shows the scatterplot that we produced in Fig. 7a where we compared the position of the nodes in ResIN with the mean of the IC curves when using real data. However, in this case, we also added the scatterplot for MDS (orange) as well as the dashed red line representing where points should be for having a perfect agreement with IRT. By the naked eye we can see that the blue points deviate less from the ideal curve. However, to avoid relying only on visualization, we also calculated the respective correlations between each method and IRT. ResIN produces a correlation of 0.976**** while MDS produces a correlation of 0.941****. Thus, both MDS and ResIN produce results extremely close to IRT in this application. One may even notice that ResIN’s correlation is larger than MDS’s one, but a single test is not sufficient to conclude that ResIN’s results are closer to IRT.

To test if really ResIN can outperform MDS, we produced 100 simulations using the graded model. Each time we produced a new set of items and responses by randomizing the parameters of the model. Even the total number of items was randomized each time between 5 and 10, and a number of levels was randomized between 3 and 6. For each simulation we compared the correlation between the x-coordinate of node’s position in each method and the mean of the equivalent IC curve. In 98% of cases ResIN produced results closer to IRT than MDS did, confirming the results previously observed with real data.

The final validation we run confirms whether the force-directed method is reproducible. This is an obvious concern, since this type of algorithm randomizes the initial position of the nodes, possibly obtaining different results each time it is run. Although all the analyses presented so far have shown great agreement between ResIN and IRT, which would not be possible if the node’s positions were subject to extensive fluctuations, here we want to better quantify the effect of the force-directed method by keeping the network constant and re-running only the force-directed algorithm. For each run, we collect the x-coordinates of the nodes and finally calculate the average correlations between them. For 50 simulations (which give us 1250 correlations) we obtain an average correlation of 0.99985 with a standard deviation of 2e-16. Three of these relationships are shown in Fig. 10a. This shows that while the force-directed algorithm is stochastic, and can introduce some minor random fluctuations, its effect is very minimal. Furthermore, as previously discussed, despite these fluctuations ResIN still produces closer results to IRT than MDS.

One may even ask if it would be possible to achieve such levels of correlation using a chaotic method. While the intuitive answer would be that this is impossible, here we want to confirm such results using some additional simulations. To confirm this point, we have produced a method that places nodes in completely random positions and correlates such positions with the mean of the equivalent IC curve from IRT. Repeating this process 100 times we obtain an average r-squared of 0.03 and an average p-value of 0.44. This clearly confirms that a chaotic method would not be able to produce correlation values close to the one observed in ResIN (i.e. above 0.95).

To see this even better we re-run the chaotic algorithm one million times to see how often the algorithm would produce correlations above 0.95. We found that in one million trials this case never happened. This is in perfect agreement with the p values of the different validations of ResIN. Indeed, a p-value of 10−28 (as we have found in previous sections) means that the probability of getting such a result by pure chance is 1 in 10 octillions. These what-if scenarios show that if ResIN was chaotic, it would be impossible to obtain any of the results we have shown in this article.

Conclusion

In this paper, we validate ResIN as a robust methodological approach for researchers who are studying attitude-related phenomena, particularly if they are interested in how specific response options relate to each other in an identity-laden opinion space. We developed ResIN to combine strengths from classical BNA and item-response theory. While BNA offers researchers a simple tool to extract and depict connections between items, item-response theory offers deeper insights into the ordinal (and possibly non-symmetric) structure of items by considering the difference between different item responses. Our main aim with ResIN was to provide researchers with a new tool that allows for the exploration of complex phenomena while still producing relatively simple and intuitive outputs.

By testing ResIN on empirical data from the US electoral context, we show that ResIN offers insight that neither BNA nor IRT could offer with similar ease. Indeed, ResIN allows inspection of the responses separately for different groups (e.g. Republicans and Democrats). While exposing less information than IRT, ResIN allows for the quick identification of structural response patterns (such as the split between Republicans and Democrats) which was not equally visible in either of the two other methods, and shows intuitively the non-linear and asymmetric relationships between identities and responses.

Since ResIN produces a spatial network, it offers both network-like information as well as (latent) space information. The latter is related to IRT and reflects latent constructs. Specifically, a node’s position on the x-axis is representative of different values of the main latent construct (e.g. left-right spectrum). Thus, we can quantify how extreme each attitude is within our society.

The more network-based interpretation, instead, does not assume any latent construct and it relies simply on the idea of correlation. Attitudes which are strongly correlated (i.e. are usually selected together) will also appear close to each other and be connected by a strong link. Instead, weakly related attitudes will appear further from each other. Using this interpretation, we can see which attitudes cluster together, so forming a shared set of attitudes in the population. Similarly, we can see which attitudes act as a bridge between two clusters, thus, eventually allowing dialogue between different social groups.

Notice also how the algorithm does not require the data to be ordinal, and the same method could be used, in principle, for studying also combinations of different data types, such as nominal and ordinal together. Future studies may also explore if such methodology could be reliably applied to multiple-choice items (i.e. having non-mutually exclusive responses) and if the force-directed algorithm could be adapted to include information from the negative correlations.

In sum, we believe that ResIN can be a useful and powerful tool for social scientists interested in identity structures and mechanisms underlying attitudes. Of course, we do not claim nor believe that this method should replace existing BNA methods, or IRT. Instead, these three methods allow the exploration of the attitude system at three different levels, just as a microscope, telescope, and normal vision allow us to see the world at three different levels; and each tool quickly reveals phenomena at a level of analysis that would be invisible or extremely complex to find using only the other tools.