Introduction

Shear instability arises between two materials when there is a discontinuity of the tangential velocity at the perturbation interface. The stability problem for this configuration was first noticed by Lord Kelvin1 and Helmholtz2, and is popularly known as Kelvin–Helmholtz instability (KHI). The simplest form of the configuration treats two incompressible ideal fluid layers of constant densities ρ1 and ρ2 and constant tangential velocities u1 and u2. Linearization of the governing equations shows that the amplitude ξ of the interface develops exponentially, i.e. ξ ~ ξ0 exp(σt), in which the growth rate σ has the expression of {ρ1ρ2k2 [(u1 − u2)/(ρ1 + ρ2)]2}1/23 where k is the wave number. The perturbation will grow if u1 ≠ u2. KHI in liquid or gas materials has been extensively treated in the literatures1,2,3,4,5,6,7,8,9,10,11,12,13,14. However, in contrast to the cases of fluids, KHI involving solids is historically less studied and far from deeply understood, despite the fact that KHI is a ubiquitous phenomenon in many engineering applications.

When a sliding detonation in high explosive spreads over a spherical steel capsule, the high-rate sliding motion of the explosive product induces a tangential velocity jump at the steel surface. The perturbation of 0.22 mm amplitude and 2.5 mm wavelength with plastic deformation was found in the surface fragment of the capsule because of the development of KHI along the steel surface15. The phenomenon of KHI was also detected at the interface between two closely packed metal plates (Al–Al and Al–Cu) when an oblique shock wave passed through. Bucking of the interface with periodic wavy morphology was formed16. Besides, KHI in solids is also of relevance to High Velocity Impact Welding (HVIW) which is a remarkable technique of joining a wide variety of both similar and dissimilar metals17,18,19,20,21,22. The principle of weld is by accelerating a flier workpiece with different energy sources (such as chemical explosive, repulsive magnetic field, laser-generated optical energy or electrically-driven rapid vaporization of a metallic conductor23,24,25) to a high velocity to obliquely impact a stationary workpiece. A successful weld is taken to be the emergence of wavy morphology at temperatures below the metal melting point with plastic deformation26,27. Many researchers have investigated the physical mechanism of formation of wavy interface28,29,30,31,32,33,34. Recently, the wavy pattern is considered to be the signature of a shear driven instability of a plastic material34. In addition, KHI is also a significant phenomenon in Inertial Confinement Fusion (ICF). Due to the impulsive nature of the laser-drivers in the experiments, KHI is less studied until an indirectly driven shock tube targets have been developed35,36. Both sides of an aluminum tracer foil are shocked by sustained counter-propagating shear flow to generate large velocities in the high-energy–density (HED) shear experiments on the National Ignition Facility (NIF). The formation of the wavy morphology induced by the development of KHI at metallic interface is a critical issue concerned by researchers. The wavy pattern performs the dynamic behaviors of metals which are obliquely impacted. The study of the physics of the evolution of the interface amplitude of KHI in solids is essentially valuable in practical engineering applications.

Differing from hydrodynamic instability in fluids, the physics of KHI in solids are primarily determined by the constitutive relations of the materials which present complex non-linear characteristics between the stress and the strain during deformations37. A representative feature of the non-linear behavior is the elastic–plastic (EP) transition which results in enhancing the difficulties of constructing the theory even in the linear growth stage of the instability. Drennov38 deduced the analytical theory by the classical normal mode methodology with the assumption of incompressible materials when an ideal fluid of finite thickness at a constant tangential velocity flowed over a half-space metallic medium with perfectly elastic properties. This case resembles the situation that one surface layer of metals has suffered the thermal softening. An analytical expression of a compatibility condition of the growth rate for the system was achieved after linearizing the governing equations. By considering the incapability of deriving analytical solution for elastoplastic medium, the stability boundary was coarsely estimated. Nassiri34 accomplished a more careful analysis of a system which was much closer to reality that two materials were treated as perfectly plastic behaviors. After applying the normal mode analysis to the linearized governing equations in the form of vorticity and stream function, the growth rates under different impact velocities were got by numerical solutions because of the impossibility to practice an analytical settlement. The normal mode analysis can describe the asymptotic behavior of the instability and the growth rates can be obtained. However, the characteristics of the development of the amplitude which may be affected by the properties of EP properties have not been mentioned, as well as extraordinarily complex mathematical problems are sufficiently involved in the normal mode analysis which lead to difficulties of achieving analytical formulas to deal with complex physical problems. Besides, previous theories were mainly restricted to KHI between two identical materials, though KHI usually emerges at the interface of materials with different densities. The effects of Atwood number (AT = (ρsolid − ρfluid)/(ρsolid + ρfluid)) on the development of the amplitude have not been considered in the linear analysis.

The characteristic time of the velocity jump lasted for a short pulse of about 0.15 μs to adequately activate the increment of amplitude, after the metallic interface was loaded by an oblique shock wave39. The development of amplitude in the linear stage plays a significant role in such a short time, and it is advantageous to derive approximate analytical formulas for KHI in strength mediums to detect the physical insight of the development of the perturbed interface. The system of KHI between fluid and solid corresponds to the situations of explosive product sliding over metal surface15 or one of metals undergoing thermal softening after impact38,39. In present article, an approximate theoretical model for KHI between perfectly EP solid and ideal fluid with arbitrary densities is developed to achieve explicit analytical solutions to describe the evolution of the perturbation amplitude. The analytical expressions of growth rates and amplitude motions are theoretically deduced. The verification of the model is executed by numerical simulations and then, the effects of Atwood number on the development of KHI in the linear stage is studied by the model.

Theoretical model formulation

Fundamental equations

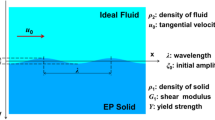
To develop the model, several assumptions are reasonably made. First, it is assumed that the main characteristics of the perturbation can be described in the two-dimensional (2D) and planar coordinates if the spanwise direction lengths of the plates perpendicular to the 2D section are long enough16,38,39. Second, on the condition that the scale of the wavelength λ is much smaller than that of material thickness h25,39, i.e. kh ≫ 1 where k = 2π/λ, it is reasonable to consider each material occupies infinite half space. Third, the plastic deformation is essentially an incompressible phenomenon with little change in densities and elastic strains are assumed to be far smaller than plastic ones. The assumption of constant densities is adopted. Forth, both of the materials are treated as uniform material properties. Fifth, the flow field is assumed to be irrotational. During the evolution of the interface, the perturbed velocity field is determined by conservation equations of the momentum with conservative or/and nonconservative forces acting on the perturbation interface. Although the nonconservative force arouses the rotation of the velocity field, the vorticity only affects a very small distance away from the interface39. With the assumption of irrotational flow field, not only the mathematical complexity is largely reduced to obtain some analytical formulas from physics insight, but also the relatively good accuracy of the model is guaranteed as shown by simulations as described in a later section.

Figure 1 shows the schematic of the KHI system in 2D Cartesian coordinates. The x-axis separates the two materials as an interface and the y-axis is oriented normal to the x-axis. Material 1 and 2 with constant density ρ1 and ρ2 occupy the upper (y > 0) and lower (y < 0) half-space respectively. Both solid and fluid have constant velocities with the values of u0,1 and u0,2 respectively in x direction. After disturbance, the interface deviates a infinitesimal distance from y = 0 to y = η (x, t) as a first-order term. The outward normal of the disturbed interface to the first-order term is

$$ {\varvec{n}} = - \frac{\partial \eta }{{\partial x}}{\varvec{i}} + {\varvec{j}}. $$
(1)
Figure 1
figure 1

The schematic of the physical model.

Full size image

For an incompressible flow, the continuity equation is

$$ \nabla \cdot {\varvec{u}}_{i} = 0, $$
(2)

where i = 1 and i = 2 represents two materials respectively, ui characterizes the irrotational perturbed velocity of material i. If the materials are irrotational at the initial moment, the irrotational properties of the flow will be maintained. ui can be expressed by the perturbed velocity potential ϕi

$$ {\varvec{u}}_{i} = \nabla \phi_{i} . $$
(3)

By combining Eq. (2), ϕi satisfies the Laplace equation. Considering each medium has a tangential velocity, a velocity potential can be written as

$$ \Phi_{i} = u_{0,i} x + \phi_{i} , $$
(4)

which still satisfies the Laplace equation.

Without conservative and nonconservative forces acting on the interface, the flow is governed by the momentum equation

$$ \rho_{i} \left[ {\frac{{\partial {\varvec{u}}_{i} }}{\partial t} + \left( {u_{0,i} \cdot \nabla } \right){\varvec{u}}_{i} } \right] = - \nabla p_{i} , $$
(5)

where pi is pressure. Integrating Eq. (5) from y = 0 to the instantaneous interface y = η (x, t) in y direction and substituting Eq. (3), it has

$$ \begin{aligned} p_{i} & = \left. {p_{i} } \right|_{y = 0} - \rho_{i} \int_{0}^{\eta } {\frac{{\partial u_{i,y} }}{\partial t}} dy - \rho_{i} u_{0,i} \int_{0}^{\eta } {\frac{{\partial u_{i,y} }}{\partial x}dy} \\ & = \left. {p_{i} } \right|_{y = 0} - \rho_{i} \int_{0}^{\eta } {\frac{{\partial^{2} \phi_{i} }}{\partial t\partial y}dy} - \rho_{i} u_{0,i} \int_{0}^{\eta } {\frac{{\partial^{2} \phi_{i} }}{\partial x\partial y}dy} \\ & = \left. {p_{i} } \right|_{y = 0} - \rho_{i} \frac{{\partial \phi_{i} }}{\partial t} + \rho_{i} \left. {\frac{{\partial \phi_{i} }}{\partial t}} \right|_{y = 0} - \rho_{i} u_{0,i} \frac{{\partial \phi_{i} }}{\partial x} + \rho_{i} u_{0,i} \left. {\frac{{\partial \phi_{i} }}{\partial x}} \right|_{y = 0} \\ & = - \left( {\rho_{i} \frac{{\partial \phi_{i} }}{\partial t} + \rho_{i} u_{0,i} \frac{{\partial \phi_{i} }}{\partial x} + C_{i} } \right), \\ \end{aligned} $$
(6)

where ui,y is the y component of the perturbed velocity. Before the interface is perturbed, we have y = η (x, t) = 0 in equilibrium, then C1 = C2.

After the interface quasi-statically departs an infinitesimal distance from y = 0 at a certain time named t = 0, the interface has the cosinusoidal form of ξ0coskx where ξ0 is the perturbation amplitude at t = 0. Because of the velocity potential in Eq. (4) depending upon x, the interface can be expressed by

$$ \eta (x,t) = \xi \left( t \right)e^{ikx} , $$
(7)

for the mathematical convenience where ξ(t) is the perturbation amplitude and the potential of the perturbed velocity is

$$ \phi_{i} = A_{i} \left( t \right)e^{ \mp ky} e^{ikx} . $$
(8)

The negative and positive signs correspond to the conditions which the velocities vanish when the distance from the interface goes to positive and negative infinity respectively.

In the process of evolution, the continuity of the normal components of the velocities at the interface is required. The kinematic conditions with the velocity potential in Eq. (4) and the interface normal in Eq. (1) are

$$ \frac{\partial \eta }{{\partial t}} = \nabla \Phi_{1} \cdot {\varvec{n}} = \nabla \Phi_{2} \cdot {\varvec{n}}. $$
(9)

After neglecting the high-order terms, the velocity continuity in the normal direction is

$$ \frac{\partial \eta }{{\partial t}} = - u_{0,1} \frac{\partial \eta }{{\partial x}} + \frac{{\partial \phi_{1} }}{\partial y} = - u_{0,2} \frac{\partial \eta }{{\partial x}} + \frac{{\partial \phi_{2} }}{\partial y}. $$
(10)

Substituting Eq. (8) into Eq. (10), we can express Ai(t) in terms of ξ(t)

$$ \dot{\xi }(t) = - kA_{1} (t) = kA_{2} (t) - iku_{0} \xi \left( t \right), $$
(11)

where the dot above ξ(t) means taking the derivative of ξ(t). It needs to be explained that the 2D coordinates system is fixed to the material 1 while deriving Eq. (11), i.e. u0,1 = 0 and u0,2 = u0. The reason is that the key of producing KHI is the relative discrepancy between the tangential velocities at perturbation interface but not the absolute values of tangential velocities. Therefore, u0 is the velocity jump in x direction at the interface.

Furthermore, the force equilibrium at the interface to the first order approximation is also required

$$ p_{1} - p_{2} + \sum\limits_{j} {F_{y}^{\left( j \right)} } = 0, $$
(12)

where Fy(j) denotes forces per unitary surface acting on both sides of the interface in the vertical direction. Fy(j) can be surface tension, viscosity, elasticity, plasticity or nonconservative force. In the system of KHI, the EP solid and ideal fluid are placed beyond and beneath the x-axis respectively, and the force due to EP properties of the solid acts on the perturbed interface. Thus, Eq. (12) becomes

$$ p_{1} - p_{2} - S_{1,yy}^{{\left( {ep} \right)}} = 0\;, $$
(13)

where S1,yy(ep) represents the vertical component of the deviatoric stress for solid in elastic or plastic state.

The force equilibrium is first applied to the perfectly elastic solid whose constitutive relation has the linear form, i.e. Hookean solid40

$$ \dot{S}_{1,ij} = 2G_{1} D_{1,ij} , $$
(14a)
$$ D_{1,ij} = \frac{1}{2}\left( {\frac{{\partial u_{1,i} }}{{\partial x_{j} }} + \frac{{\partial u_{1,j} }}{{\partial x_{i} }}} \right), $$
(14b)

where G1 is the shear modulus and D1,ij is the strain rate tensor. By combining Eqs. (3) and (8), the strain rate tensor becomes

$$ D_{1,ij} = A_{1} \left( t \right)e^{ikx - ky} k^{2} \left[ {\begin{array}{*{20}c} { - 1} & { - i} \\ { - i} & 1 \\ \end{array} } \right]. $$
(15)

Then, combining Eq. (11) and integrating Eq. (14a) from the initial perturbed interface η(x, 0) = ξ0eikx, the stress tensor S1,ij can be obtained

$$ S_{1,ij} = - 2G_{1} k\left( {\xi - \xi_{0} } \right)e^{ikx - ky} \left[ {\begin{array}{*{20}c} { - 1} & { - i} \\ { - i} & 1 \\ \end{array} } \right]. $$
(16)

Thus, the vertical component of the deviatoric stress in the elastic regime is

$$ S_{1,yy}^{{\left( {ep} \right)}} = - 2G_{1} k\left( {\xi - \xi_{0} } \right)e^{ikx - ky} . $$
(17)

Substituting Eqs. (6) and (17) into Eq. (13), we have the motion equation of the perturbation amplitude in perfectly elastic solid

$$ \ddot{\xi } + \frac{{2\rho_{2} u_{0} ki}}{{\rho_{1} + \rho_{2} }}\dot{\xi } - \frac{{\rho_{2} u_{0}^{2} k^{2} }}{{\rho_{1} + \rho_{2} }}\xi = - \frac{{2G_{1} k^{2} }}{{\rho_{1} + \rho_{2} }}\left( {\xi - \xi_{0} } \right). $$
(18)

If the effective stress

$$ \overline{\sigma } = \sqrt {\tfrac{3}{2}S_{1,ij} S_{1,ij} } , $$
(19)

arrives at Y which is the yield stress of the solid, the solid will mechanically transit from the elastic regime into the plastic regime. By substituting Eq. (16), it has

$$ \overline{\sigma }^{2} = \frac{3}{2}S_{1,ij} S_{1,ij} = 12e^{ - 2ky} G_{1}^{2} k^{2} \left( {\xi - \xi_{0} } \right)^{2} . $$
(20)

Here, only the real components of the stress tensor are kept during deriving the effective stress due to express the cosinusoidal form of the interface as Eq. (7) for the mathematical convenience. Considering the plastic deformation only occurs at a small layer from the interface39, we take y = k-1 in Eq. (20) to get a better fit with numerical simulation results and find the perturbation amplitude ξp at when the elastic–plastic transition takes place

$$ \xi_{p} - \xi_{0} \approx \frac{eY}{{2\sqrt 3 G_{1} k}}. $$
(21)

Then, the vertical component of the deviatoric stress in the plastic regime becomes

$$ S_{1,yy}^{{\left( {ep} \right)}} = - \frac{eY}{{\sqrt 3 }}\;e^{ikx - ky} . $$
(22)

Combining Eq. (18), the motion equation of the amplitude of the perturbation interface in KHI between EP solid and ideal fluid can be achieved

$$ \ddot{\xi } + \frac{{2\rho_{2} u_{0} ki}}{{\rho_{1} + \rho_{2} }}\dot{\xi } - \frac{{\rho_{2} u_{0}^{2} k^{2} }}{{\rho_{1} + \rho_{2} }}\xi = - \left\{ \begin{gathered} \frac{{2G_{1} k^{2} }}{{\rho_{1} + \rho_{2} }}\left( {\xi - \xi_{0} } \right)\;,\quad \xi \le \xi_{p} \hfill \\ \frac{e}{\sqrt 3 }\frac{kY}{{\rho_{1} + \rho_{2} }}\;.\quad \quad \;\;\xi > \xi_{p} \hfill \\ \end{gathered} \right. $$
(23)

For two ideal fluids, the above equation degrades into

$$ \ddot{\xi } + \frac{{2\rho_{2} u_{0} ki}}{{\rho_{1} + \rho_{2} }}\dot{\xi } - \frac{{\rho_{2} u_{0}^{2} k^{2} }}{{\rho_{1} + \rho_{2} }}\xi = 0, $$
(24)

which is the same as previous result6.

It is convenient to write Eq. (23) as

$$ \ddot{\xi } + 2M_{1} i\;\dot{\xi } = \left\{ \begin{gathered} \Lambda \xi_{0} - \left( {\Lambda - M_{2} } \right)\xi \;,\quad \xi \le \xi_{p} \hfill \\ M_{2} \xi - {\rm X}\;,\quad \quad \quad \quad \;\,\xi > \xi_{p} \hfill \\ \end{gathered} \right. $$
(25)

with the definitions of

$$ M_{1} = \frac{{\rho_{2} u_{0} k}}{{\rho_{1} + \rho_{2} }},M_{2} = \frac{{\rho_{2} u_{0}^{2} k^{2} }}{{\rho_{1} + \rho_{2} }},\Lambda = \frac{{2G_{1} k^{2} }}{{\rho_{1} + \rho_{2} }},{\rm X} = \frac{e}{\sqrt 3 }\frac{kY}{{\rho_{1} + \rho_{2} }}. $$
(26)

The corresponding initial conditions are

$$ \xi \left( 0 \right) = \xi_{0} ,\quad \quad \dot{\xi }\left( 0 \right) = 0. $$
(27)

Growth rate

The eigenvalue function of Eq. (25) is the dispersion relation

$$ n^{2} + 2M_{1} i\;n = \left\{ \begin{gathered} - \left( {\Lambda - M_{2} } \right),\quad \xi \le \xi_{p} \hfill \\ M_{2} ,\quad \quad \quad \quad \xi > \xi_{p} \hfill \\ \end{gathered} \right. $$
(28)

where n is the eigenvalue. Equation (28) is a quadratic polynomial formula that has complex solutions. In the elastic branch, the solutions are

$$ \begin{aligned} n_{e} & = - M_{1} i \pm \sqrt { - M_{1}^{2} - \left( {\Lambda - M_{2} } \right)} \\ & = - \frac{{\rho_{2} ku_{0} }}{{\rho_{1} + \rho_{2} }}i \pm \frac{{k\sqrt {\rho_{1} \rho_{2} u_{0}^{2} - 2G_{1} \left( {\rho_{1} + \rho_{2} } \right)} }}{{\rho_{1} + \rho_{2} }}, \\ \end{aligned} $$
(29)

where the index e denotes the elastic state of the solid. Equation (29) can be degenerated to the case of two ideal fluids which is the same as Ref.6. ne may contain real and imaginary parts. If the following condition in Eq. (30) is satisfied

$$ u_{0} > u_{0,cr} = \sqrt {2G_{1} \frac{{\rho_{1} + \rho_{2} }}{{\rho_{1} \rho_{2} }}} = \sqrt {\frac{{4G_{1} }}{{\rho_{1} \left( {1 - A_{T} } \right)}}} , $$
(30)

where u0,cr is the critical value of the tangential velocity jump, the formula in the radical sign in Eq. (29) is positive and ne possesses positive real part which is the growth rate determining the increment of the amplitude. Equation (30) is the condition of the presence of the growth rate and u0,cr is related to shear modulus and Atwood number. Due to normally positive G1 and Atwood number in the range of (− 1, 1), the part in the radical sign of Eq. (30) is always greater than zero which means that a critical tangential velocity is always found to obtain a growth rate. Equation (30) indicates that fluid with smaller density needs to have a larger velocity in the tangential direction to overcome the effect of the mechanical property of solid to arouse the growth of the interface. If Eq. (30) is not satisfied, only imaginary part will be left in ne which stands for the vibration frequency and the suppression of the growth.

In the plastic branch, the eigenvalue is

$$ \begin{aligned} n_{p} & = - M_{1} i \pm \sqrt { - M_{1}^{2} + M_{2} } \\ & = - \frac{{\rho_{2} ku_{0} }}{{\rho_{1} + \rho_{2} }}i \pm \frac{{k\sqrt {\rho_{1} \rho_{2} u_{0}^{2} } }}{{\rho_{1} + \rho_{2} }}, \\ \end{aligned} $$
(31)

where the index p denotes the plastic state of the solid. According to the form of Eq. (31), ρ1ρ2u02 is always positive and np always has positive real part. The growth rate constantly exits in the plastic regime which leads to the possibility of amplitude growth, however, the growth is restrained in some situations. It is noticed that the growth rate is not regarding any information of the mechanical properties of solid and has the same form as the case of two ideal fluids with different densities. The model adopts the constitutive relation of perfect plasticity, of which the yield stress is constant and independent of the strain during deformation. So, the yield stress appears in the nonhomogeneous term in Eq. (23) and does not affect the growth rate but the solution of the amplitude. The suppression effects of the yield stress on amplitude growth will be shown in the analytical solutions.

Analytical solutions for the perturbation amplitude

In order to solve Eq. (25) analytically, the following transformations are introduced

$$ x_{1} = \left[ {\Lambda \xi_{0} - \left( {\Lambda - M_{2} } \right)\xi } \right]e^{{iM_{1} t}} ,\quad \quad \xi \le \xi_{p} $$
(32a)
$$ x_{2} = \left( {M_{2} \xi - {\rm X}} \right)e^{{iM_{1} t}} \;,\quad \quad \,\xi > \xi_{p} $$
(32b)

and the two branches of Eq. (25) become

$$ \ddot{x}_{1} = \left[ { - M_{1}^{2} - \left( {\Lambda - M_{2} } \right)} \right]x_{1} \;,\quad \quad \xi \le \xi_{p} $$
(33a)
$$ \ddot{x}_{2} = \left( { - M_{1}^{2} + M_{2} } \right)x_{2} ,\quad \quad \xi > \xi_{p} $$
(33b)

which must follow the conditions of

$$ x_{1} \left( 0 \right) = M_{2} \xi_{0} \;,\quad \dot{x}_{1} \left( 0 \right) = iM_{1} M_{2} \xi_{0} \;, $$
(34a)
$$ x_{1} \left( {t_{p} } \right) = x_{2} \left( {t_{p} } \right) = x_{p} \;, $$
(34b)
$$ \dot{x}_{1} \left( {t_{p} } \right) = \dot{x}_{1p} ,\quad \dot{x}_{2} \left( {t_{p} } \right) = \dot{x}_{2p} , $$
(34c)

where tp is the time when the solid transients from elasticity to plasticity.

The solution of the amplitude can be derived by integrating the transformed motion equations. For the elastic branch, integration is conducted twice starting from Eq. (33a) with the initial conditions of Eq. (34a). Then, the transformation is inverted by substituting Eq. (32a) to get ξ(t) in the elastic state. Next, the same method is proceeded on Eq. (33b) for the plastic branch with the conditions of Eqs. (34b) and (34c) to derive ξ(t). Consequently, the solutions with complete analytical expressions for stable and unstable states are achieved.

Two stable solutions are

$$ \xi \left( t \right) = \frac{{\xi_{0} }}{{\Lambda - M_{2} }}\left\{ {\Lambda - \frac{1}{2}M_{2} e^{{ - iM_{1} t}} \left[ {\left( {1 + \frac{{M_{1} }}{{\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{i\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} t}} + \left( {1 - \frac{{M_{1} }}{{\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{ - i\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} t}} } \right]} \right\}\;\;, $$
(35)

for the purely elastic case below the transition point and

$$ \xi \left( t \right) = \left\{ \begin{gathered} \frac{{\xi_{0} }}{{\Lambda - M_{2} }}\left\{ {\Lambda - \frac{1}{2}M_{2} e^{{ - iM_{1} t}} \left[ {\left( {1 + \frac{{M_{1} }}{{\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{i\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} t}} + \left( {1 - \frac{{M_{1} }}{{\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{ - i\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} t}} } \right]} \right\}\;,\quad t \le t_{p} \hfill \\ \frac{1}{{M_{2} }}\left\{ {X + \frac{1}{2}e^{{ - iM_{1} t}} \left[ {\left( {x_{p} + \frac{{\dot{x}_{2p} }}{{\sqrt { - M_{1}^{2} + M_{2} } }}} \right)e^{{\left( {t - t_{p} } \right)\sqrt { - M_{1}^{2} + M_{2} } }} + \left( {x_{p} - \frac{{\dot{x}_{2p} }}{{\sqrt { - M_{1}^{2} + M_{2} } }}} \right)e^{{ - \left( {t - t_{p} } \right)\sqrt { - M_{1}^{2} + M_{2} } }} } \right]} \right\}\;,\quad t_{p} \le t \le t_{m} \hfill \\ \xi_{m} - \frac{{X - M_{2} \xi_{m} }}{{\Lambda - M_{2} }}\left\{ {1 - \frac{1}{2}e^{{ - iM_{1} \left( {t - t_{m} } \right)}} \left[ {\left( {1 + \frac{{M_{1} }}{{\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{i\left( {t - t_{m} } \right)\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }} + \left( {1 - \frac{{M_{1} }}{{\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{ - i\left( {t - t_{m} } \right)\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }} } \right]} \right\}\;,t \ge t_{m} \hfill \\ \end{gathered} \right. $$
(36)

for − M12 − (Λ − M2) < 0 with EP transition. tp is got by an implicit form by evaluating the first branch of Eq. (36) with ξp, and xp is given by evaluating Eq. (32a) at t = tp

$$ x_{p} = \left[ {\Lambda \xi_{0} - \left( {\Lambda - M_{2} } \right)\xi_{p} } \right]e^{{iM_{1} t_{p} }} .\quad \quad \xi \le \xi_{p} \; $$
(37)

Besides, it has

$$ \dot{x}_{2p} = \frac{1}{{\Lambda - M_{2} }}\left\{ {x_{p} M_{1} \Lambda i + M_{2} \sqrt {\left[ { - M_{1}^{2} - \left( {\Lambda - M_{2} } \right)} \right]x_{p}^{2} + \left( {\Lambda - M_{2} } \right)\left( {M_{2} \xi_{0} } \right)^{2} } } \right\}, $$
(38)

which is obtained by taking derivatives of Eqs. (32a) and (32b), then eliminating \(\dot{\xi }\) from those two expressions and evaluating them at t = tp with xp and \({\dot{\text{x}}}_{1p}\) which is derived by integrating Eq. (33a) once and evaluating it at t = tp. tm in Eq. (36) is the time of achieving the maximum amplitude ξm after plastic transition (tp ≤ t ≤ tm) and the amplitude evolution goes back to perfectly elastic state after tm.

Two unstable solutions are, respectively,

$$ \xi \left( t \right) = \left\{ \begin{gathered} \frac{{\xi_{0} }}{{\Lambda - M_{2} }}\left\{ {\Lambda - \frac{1}{2}M_{2} e^{{ - iM_{1} t}} \left[ {\left( {1 + \frac{{M_{1} }}{{\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{i\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} t}} + \left( {1 - \frac{{M_{1} }}{{\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{ - i\sqrt {M_{1}^{2} + \left( {\Lambda - M_{2} } \right)} t}} } \right]} \right\}\;,\quad t \le t_{p} \hfill \\ \frac{1}{{M_{2} }}\left\{ {X + \frac{1}{2}e^{{ - iM_{1} t}} \left[ {\left( {x_{p} + \frac{{\dot{x}_{2p} }}{{\sqrt { - M_{1}^{2} + M_{2} } }}} \right)e^{{\left( {t - t_{p} } \right)\sqrt { - M_{1}^{2} + M_{2} } }} + \left( {x_{p} - \frac{{\dot{x}_{2p} }}{{\sqrt { - M_{1}^{2} + M_{2} } }}} \right)e^{{ - \left( {t - t_{p} } \right)\sqrt { - M_{1}^{2} + M_{2} } }} } \right]} \right\}\;,\quad t \ge t_{p} \hfill \\ \end{gathered} \right. $$
(39)

for the case of − M12 − (Λ − M2) < 0, and

$$ \xi \left( t \right) = \left\{ \begin{gathered} \frac{{\xi_{0} }}{{\Lambda - M_{2} }}\left\{ {\Lambda - \frac{1}{2}M_{2} e^{{ - iM_{1} t}} \left[ {\left( {1 + \frac{{iM_{1} }}{{\sqrt { - M_{1}^{2} - \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{t\sqrt { - M_{1}^{2} - \left( {\Lambda - M_{2} } \right)} }} + \left( {1 - \frac{{iM_{1} }}{{\sqrt { - M_{1}^{2} - \left( {\Lambda - M_{2} } \right)} }}} \right)e^{{ - t\sqrt { - M_{1}^{2} - \left( {\Lambda - M_{2} } \right)} }} } \right]} \right\}\;,\quad t \le t_{p} \hfill \\ \frac{1}{{M_{2} }}\left\{ {X + \frac{1}{2}e^{{ - iM_{1} t}} \left[ {\left( {x_{p} + \frac{{\dot{x}_{2p} }}{{\sqrt { - M_{1}^{2} + M_{2} } }}} \right)e^{{\left( {t - t_{p} } \right)\sqrt { - M_{1}^{2} + M_{2} } }} + \left( {x_{p} - \frac{{\dot{x}_{2p} }}{{\sqrt { - M_{1}^{2} + M_{2} } }}} \right)e^{{ - \left( {t - t_{p} } \right)\sqrt { - M_{1}^{2} + M_{2} } }} } \right]} \right\}\;,\quad t \ge t_{p} \hfill \\ \end{gathered} \right. $$
(40)

for the case of − M12 − (Λ − M2) > 0.

Numerical simulations

Numerical simulations of KHI are inserted to state the reliability of the theoretical model. The perturbation growth factor which is the ratio of the amplitude history to the initial amplitude (i.e. ξ(t)/ξ0) is defined. The verification is implemented by comparing the growth factors obtained by model and simulations.

The numerical scheme is taken to be a 2D Lagrange method which has been adopted to simulate oblique shock wave impact problems and other hydrodynamic instability phenomena frequently38,39. Meshes are fixed to the material geometries at the initial moment and transform with the motion of the materials in the Lagrange method which can capture the material interface clearly. The framework of the Lagrange method is illustrated in the Ref.41 in details and the finite element method will be not presented specifically here.

Two plates are considered in Cartesian planar coordinates in the simulations. The initial conditions are shown in Fig. 2. The initial amplitude (2ξ0) which is the distance from wave crest to trough in the y direction is 20 μm and the wavelength is 250 μm which are representative characteristic scales in oblique impact25,39. Both of the thicknesses of two plates are set to be 2 mm to guarantee kh1 ≫ 1 and kh2 ≫ 1, where h1 and h2 are the thicknesses for solid and fluid respectively, to ensure the developments of the instabilities behave like half mediums. The lengths of two plates in the x direction contain twenty wavelengths to diminish the effect of lateral extents. Square meshes with the size of 2.5 μm are distributed near the interface at the initial moment. The solid plate is quiescent and the tangential velocity of the fluid plate is set to be u0 at the initial time.

Figure 2
figure 2

The material interface at initial moment.

Full size image

The properties of solid and fluid are simulated with a Mie-Grüneisen EOS with a coefficient Г = ρ0Г0/ρ, where Г0 is a parameter characteristic of a material and ρ0 is the density under normal conditions. The shock velocity vs is assumed to linearly varies with the particle velocity vp, i.e. vs = c0 + svp, where c0 and s are characteristic constants of the material. The solid material is set to be copper which appears in the oblique impact experiment16, as the fluid is set to be water. The parameters of EOS for solid and fluid are listed in Table 1. In the simulations, a value of 10c0 is taken to the original c0 in Table 1 to ensure incompressibility. Besides, a perfectly elastic and rigid plastic model is adopted to characterize the copper. The values of the shear modulus G1 and the yield strength Y are taken as constants. The specific values of G1 and Y are also given in Table 1.

Table 1 Parameters in simulations for solid and fluid42,43,44.
Full size table

Although the verification of the Lagrange code has been applied in Ref.41, the situation in Ref.41 is not completely consistent with that we settle here. Hence, the evolution of the amplitude in KHI by numerical simulation is compared with the classical theoretical formulation of two ideal fluids to perform the credibility by considering lack of the experiment at the same condition of the theoretical analysis. As regarding the simplest case of identical ideal fluids, the amplitude by classical theory varies exponentially with time corresponding to the situation of AT = 0 in the linear growth stage38,39,45

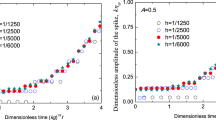
$$ \xi \left( t \right) \sim \xi_{0} \cosh \left( {\frac{{ku_{0} }}{2}t} \right). $$
(41)

Three comparisons at different u0, i.e. 0.5, 1.5, 4.0 mm/μs, are practiced in Fig. 3a. The growth factors calculated by numerical code and theoretical formulation in Eq. (41) have good agreements in the early growth phase. The divergences in the late time are detected due to the departure of the linear growth stage. Furthermore, the amplitude for two ideal fluids with distinct densities by theory is

$$ \xi \left( t \right) \sim \xi_{0} \cosh \left( {\sqrt {\frac{{\rho_{1} \rho_{2} }}{{\left( {\rho_{1} + \rho_{2} } \right)^{2} }}} ku_{0} t} \right). $$
(42)
Figure 3
figure 3

Growth factors versus time by numerical simulations and classical theory of KHI between two ideal fluids: (a) u0 = 0.5, 1.5, 4.0 mm/μs as AT = 0, (b) AT = 0.7980, 0.4958, 0.0 as u0 = 1.0 mm/μs.

Full size image

Figure 3b plots the growth factors by numerical method and Eq. (42) at u0 = 1 mm/μs at different Atwood number. ρ1 is set to be 8.9 g/cm3 and ρ2 is altered to obtain different Atwood numbers with values of 1.0, 3.0 and 8.9 g/cm3 respectively. Good comparisons in the early stage are shown again.

After perform the credibility of the Lagrange code, the growth factors achieved by the analytical solutions of the amplitude are plotted in company with the growth factors by simulations in Fig. 4 where two stable solutions and two unstable solutions are shown. The copper is stationary at the initial moment and the water with relative tangential velocity is set below. The material properties of solid and fluid in Table1 are also adopted. The conditions, including initial amplitude, wavelength, tangential velocities and material parameters are identical in the theoretical model and simulations. The stable cases correspond to u0 = 1.0 mm/μs, ρ2 = 2.0 g/cm3 and u0 = 1.0 mm/μs, ρ2 = 2.5 g/cm3, as the unstable cases correspond to u0 = 1.0 mm/μs, ρ2 = 3.0 g/cm3 and u0 = 2.0 mm/μs, ρ2 = 1.0 g/cm3. The growth factors by model are basically consistent with those by simulations. Main characteristics of growth factors are obtained by the model, such as the oscillations in the stable case and the growths as the interface is unstable. The limited differences may because the discontinuity of tangential velocities near the interface always maintains in the model whereas a continuous profile of the tangential velocity is gradually established in the simulation.

Figure 4
figure 4

Growth factors versus time by model and simulation of KHI between perfectly EP solid and ideal fluid.

Full size image

Results and discussion

Characteristics of the evolution of the perturbation amplitude and effects of Atwood number based on the theoretical model are illustrated particularly in this section. The developments of KHI between EP solid and ideal fluid at u0 = 1.0 mm/μs with different AT are plots in Fig. 5a. Material interface is the same as that in Fig. 2 i.e. ξ0 = 10 μm and λ = 250 μm. The solid plate is also set as copper with the mechanical parameters listed in Table 1, i.e. ρ1 = 8.9 g/cm3, G1 = 39.38 GPa, Y = 0.5 GPa. The values of ρ2 are taken to be 1.0, 1.5, 2.0, 2.5, 3.0, 5.0 and 13.0 g/cm3 to get the values of AT to be 0.7980, 0.7115, 0.6330, 0.5614, 0.4958, 0.2806 and -0.1872 respectively. When AT equals 0.7980 or 0.7115, the interface is stable in the purely elastic stage. According to Eq. (30), u0 is smaller than the critical velocity. The eigenvalue in Eq. (29) has only the imaginary part which means an oscillation frequency. The amplitudes follow the solution in Eq. (35). The growth factors vibrate around small values and the amplitudes are always below the plastic transition point ξp in Eq. (21). The growth of the interface is controlled by the mechanical properties G1. The amplitude increases slightly as AT decreases from 0.7980 to 0.7115. In the cases of AT = 0.6330 and 0.5614, u0 is still smaller than the critical velocity and the amplitudes perform the vibration behaviors. Yet, the vibration is strong enough to achieve the EP transition point. After solid transforms from elastic state into plastic state, the amplitudes grow to maximum value ξm at time tm by the suppression of material yield stress, even though there is always a growth rate in the plastic regime as shown in Eq. (31). Since arriving at the maximum value, the evolutions of the amplitudes go back to the elastic state to oscillate near the maximum amplitude based on Eq. (36). For the cases of AT = 0.4958, 0.2806 and -0.1872, the interface also vibrates from elastic state to plastic state after EP transition point. However, the growth of amplitude cannot be suppressed by the yield stress. The growth factors keep the trends of increments according to the solution in Eq. (39). The KHI system is unstable under these situations. The slope of the growth factor of AT = 0.4958 is obviously less than that of AT = 0.2806 and − 0.1872. The speed of the growth with AT = − 0.1872 is the most rapid in the seven AT cases in Fig. 5a.

Figure 5
figure 5

Growth factors vs time with AT = 0.7980, 0.7115, 0.6330, 0.5614, 0.4958, 0.2806 and − 0.1872 at u0 by analytical model: (a) u0 = 1 mm/μs, (b) u0 = 1.2 mm/μs, (c) u0 = 1.5 mm/μs, (d) u0 = 2.0 mm/μs.

Full size image

Furthermore, the tangential velocity u0 is enhanced and other parameters are fixed the same as the conditions in Fig. 5a. Three more values of u0 = 1.2, 1.5 and 2.0 mm/μs are exhibited in Fig. 5b,c and d respectively. Under disparate velocities, the effects of Atwood number on the developments of the perturbation display distinct features. As the velocity varying from 1.0 mm/μs to 1.2 mm/μs, the development of the growth factor of case AT = 0.7980 is still stable in the purely elastic stage just with the increase of the amplitude. For the case of AT = 0.7115, the characteristics of the growth factor convert from the elastic vibration in Fig. 5a to the plastic stable state in Fig. 5b. The suppression mode of the growth is controlled by Y, not by G1. As noticed in the cases of AT = 0.6330, 0.5614, 0.4958, 0.2806 and − 0.1872, every interface is unstable. When the velocity arrives at 1.5 mm/μs in Fig. 5c, except for the largest one of the seven AT, the systems of KHI between EP solids and ideal fluids grow rapidly to be unstable. The stable one follows the solution in Eq. (36) but not the purely elastic one in Eq. (35). For an even higher velocity u0 = 2.0 mm/μs, none stable interface is detected in the Fig. 5d.

Figure 6a and b plot the growth factors with the same parameters in Fig. 5a except for Y = 0.4 GPa and Y = 0.3 GPa. A purely elastic solution as AT = 0.7980 are observed in Fig. 6a as Y = 0.4 GPa. The growth factor vibrates beneath ξp and the interface maintains the stable state. Two stable examples with EP transition as AT = 0.7115 and 0.6330 are also given in Fig. 6a. The amplitudes remain elastic oscillation after growing into the plastic stage. In the latter cases as AT = 0.5614, 0.4958, 0.2806 and -0.1872, the perturbation amplitudes are unstable and increase with different slopes. As expected, the amplitude with the largest ρ2 i.e. AT = -0.1872, develops fastest. By decreasing the yield stress to 0.3GPa, as shown in Fig. 6b, each of the stable cases as AT = 0.7980 and 0.7115 follows Eq. (36) with EP transition. Purely elastic solution is not found as Y = 0.3 GPa in the seven AT cases. For the other five AT, the systems of KHI are unstable after the amplitudes have grown sufficiently to the plastic regime. As shown in Fig. 6a and b, the suppression effects of yield strength diminish as reducing Y.

Figure 6
figure 6

Growth factors vs time with AT = 0.7980, 0.7115, 0.6330, 0.5614, 0.4958, 0.2806 and − 0.1872 at different Y by analytical model: (a) Y = 0.4 GPa, (b) Y = 0.3 GPa.

Full size image

Another aspect is discussed to perform some features when the initial amplitude varies. Compared with conditions in Fig. 5a, ξ0 is changed to be 5 μm and 20 μm. The growth factors for the two values of ξ0 are presented in Fig. 7a and b respectively. In Fig. 7a, cases of AT = 0.7980, 0.7115, 0.6330, 0.5614 and 0.4958 as ξ0 = 5 μm are stable in the purely elastic regime under the EP transition point ξp. As the expression in Eq. (21), ξp is determined by ξ0 and a term with regard to k, G1 and Y. The decrement of ξ0 diminishes ξp apparently but enhances the ratio of ξp and ξ0 because k, G1 and Y are fixed. The amplitude of the elastic oscillation increases as AT decreases. In the case of AT = 0.2806, the interface experiences EP transition and then oscillates elastically. The growth factor losses stability after EP transition as AT = − 0.1872. Afterwards, to investigate the amplitude evolution of the initial amplitude with larger value, ξ0 is raised to 20 μm and the growth factors with the upper seven AT are plotted in Fig. 7b. ξp/ξ0 decreases and the case of AT = 0.7980 follows the stable solution with EP transition. The other six KHI systems are unstable.

Figure 7
figure 7

Growth factors vs time with AT = 0.7980, 0.7115, 0.6330, 0.5614, 0.4958, 0.2806 and − 0.1872 with different ξ0 by analytical model: (a) ξ0 = 5 μm, (b) ξ0 = 20 μm.

Full size image

The above results indicate that the evolution of the perturbation interface in KHI system between EP solid and ideal fluid is influenced by AT. The developments of the amplitude perform disparate behaviors as varying AT when other parameters are invariable. With decreasing AT, the system changes from stable state to unstable state. The purely elastic stable state is controlled by G1, as well as the stable state with plastic transition is affected by the EP properties of solid. The vibration of the amplitude is detected in both of the stable situations. As the density of fluid increases, the amplitude grows to lose stability. For the cases of AT = 0.7980 and 0.7115 in the three groups of different u0, Y and ξ0, the evident distinctions of the evolution of the amplitude are explored. The characteristics of the amplitude motion are prominently governed by the EP constitutive relation to present various trends of stable and unstable states. But, for the case of AT = − 0.1872, the amplitude increases in each situation and the suppression effects of the EP properties of solid seem to be invalid. Therefore, an inspiration is brought that it is necessary to pay attention on the suppression effects of EP properties which may influence the formation of the wavy morphology while plates with large AT are suffering obliquely impact.

Conclusion

The evolution of the amplitude and the Atwood number effects in KHI system between EP solid and ideal fluid is discussed by developing an approximate theoretical model which is convenient to derive the analytical solution of the perturbation amplitude in present study.

Based on the assumptions of incompressible and irrotational flow field, the velocities are expressed by the velocity potentials. Arbitrary densities are contained in the momentum equations which are integrated to obtain pressures. Based on the continuity of normal velocities and force equilibrium with non-linear EP mechanical properties of solid at interface, the governing equations for the motion of the amplitude can be achieved. It is possible to solve the motion equations by some transformations and integrations to obtain completely analytical solutions which have two stable and two unstable expressions. The understanding of KHI can be quantitatively analyzed when the surface of EP solid is flowed over by ideal fluid with constant tangential velocities.

The verification is actualized by comparing the distributions of the growth factors by 2D Lagrange simulations and theoretical model. The credibility of the model is performed by the consistent results for both stable and unstable cases. The evolution of the amplitude can be described by the theoretical model.

Several groups of the growth factors by the model are presented in the article. One stable evolution of the amplitude in the purely elastic stage exhibits the behavior of vibration below the EP transition point under the suppression of solid shear modulus which controls the growth rate. By mentioning the other stable solution with EP transition, the amplitude elastically vibrates sufficiently to transform from elastic to plastic regime, and remains oscillating elastically after it grows to a maximum point in the plastic regime. The yield strength governs the motion of the amplitude after plastic transition but not by preventing the growth rate. For the unstable case, the system losses stability after EP transition and the amplitude keeps increasing. As Atwood number decreasing, the perturbed interface deviates from stable to unstable situations. The controlling effects of EP properties play a dominant role on the development processes with large AT. When two different plates with large AT undergo oblique impact, the EP mechanical properties of the solid may need to be considered carefully in the analysis of the evolution of KHI. The relevant research will be investigated particularly in future work.