Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Quantized fractional Thouless pumping of solitons

Nature Physics volume 19, pages 420–426 (2023)Cite this article

Subjects

Abstract

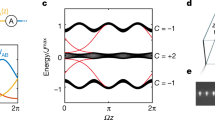
In many contexts, interaction between particles gives rise to emergent phenomena. An example is the fractional quantum Hall effect, where the interaction between electrons leads to fractionally quantized Hall conductance. In photonic systems, the nonlinear response of an ambient medium mediates the interaction between photons, and, in the mean-field limit, these dynamics are described by the nonlinear Schrödinger (also called Gross–Pitaevskii) equation. It was recently shown that at weak nonlinearity, soliton motion in nonlinear Thouless pumps—a dimensionally reduced implementation of a Chern insulator—could be quantized to the Chern number, because solitons track the single-band Wannier function throughout the pumping cycle. Here using arrays of coupled optical waveguides, we show that a sufficiently strong nonlinearity fractionally quantizes the motion of solitons. Specifically, we find that the soliton follows maximally localized multi-band Wannier functions and therefore returns to itself only after multiple cycles of the Thouless pump—but displaced by an integer number of unit cells—leading to a rich fractional plateau structure describing soliton motion. Our results represent an example of emergent behaviour in topologically non-trivial systems in the presence of interactions.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Model for quantized fractional Thouless pumping.
Fig. 2: Theory of quantized fractional Thouless pumping.
Fig. 3: Experimental observation of an f = −1/2 fractionally pumped soliton.
Fig. 4: Average centre-of-mass displacement per period, 〈x〉, calculated for an off-diagonal AAH model with 13 bands.

Similar content being viewed by others

Data availability

Data that support the findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.

References

  1. Klitzing, K. V., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).

    ADS  Google Scholar 

  2. Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).

    ADS  Google Scholar 

  3. Simon, B. Holonomy, the quantum adiabatic theorem, and Berry’s phase. Phys. Rev. Lett. 51, 2167–2170 (1983).

    MathSciNet  ADS  Google Scholar 

  4. Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).

    ADS  Google Scholar 

  5. Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).

    ADS  Google Scholar 

  6. Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).

    ADS  Google Scholar 

  7. Jain, J. K. Composite Fermions (Cambridge Univ. Press, 2007).

  8. Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).

    ADS  Google Scholar 

  9. Raghu, S. & Haldane, F. D. M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 78, 033834 (2008).

    ADS  Google Scholar 

  10. Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).

    ADS  Google Scholar 

  11. Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013).

    ADS  Google Scholar 

  12. Atala, M. et al. Direct measurement of the Zak phase in topological Bloch bands. Nat. Phys. 9, 795–800 (2013).

    Google Scholar 

  13. Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014).

    ADS  Google Scholar 

  14. Aidelsburger, M. et al. Measuring the Chern number of Hofstadter bands with ultracold bosonic atoms. Nat. Phys. 11, 162–166 (2015).

    Google Scholar 

  15. Süsstrunk, R. & Huber, S. D. Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47 (2015).

    ADS  Google Scholar 

  16. Nash, L. M. et al. Topological mechanics of gyroscopic metamaterials. Proc. Natl Acad. Sci. USA 112, 14495–14500 (2015).

    ADS  Google Scholar 

  17. Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).

    MathSciNet  ADS  Google Scholar 

  18. Zeuner, J. M. et al. Observation of a topological transition in the bulk of a non-Hermitian system. Phys. Rev. Lett. 115, 040402 (2015).

    ADS  Google Scholar 

  19. Smirnova, D., Leykam, D., Chong, Y. & Kivshar, Y. Nonlinear topological photonics. Appl. Phys. Rev. 7, 021306 (2020).

    ADS  Google Scholar 

  20. Clark, L. W., Schine, N., Baum, C., Jia, N. & Simon, J. Observation of Laughlin states made of light. Nature 582, 41–45 (2020).

    ADS  Google Scholar 

  21. Lumer, Y., Plotnik, Y., Rechtsman, M. C. & Segev, M. Self-localized states in photonic topological insulators. Phys. Rev. Lett. 111, 243905 (2013).

    ADS  Google Scholar 

  22. Mukherjee, S. & Rechtsman, M. C. Observation of Floquet solitons in a topological bandgap. Science 368, 856–859 (2020).

    ADS  Google Scholar 

  23. Ablowitz, M. J., Curtis, C. W. & Ma, Y.-P. Linear and nonlinear traveling edge waves in optical honeycomb lattices. Phys. Rev. A 90, 023813 (2014).

    ADS  Google Scholar 

  24. Leykam, D. & Chong, Y. D. Edge solitons in nonlinear-photonic topological insulators. Phys. Rev. Lett. 117, 143901 (2016).

    ADS  Google Scholar 

  25. Mukherjee, S. & Rechtsman, M. C. Observation of unidirectional solitonlike edge states in nonlinear Floquet topological insulators. Phys. Rev. X 11, 041057 (2021).

    Google Scholar 

  26. Maczewsky, L. J. et al. Nonlinearity-induced photonic topological insulator. Science 370, 701–704 (2020).

    MathSciNet  ADS  Google Scholar 

  27. Xia, S. et al. Nontrivial coupling of light into a defect: the interplay of nonlinearity and topology. Light Sci. Appl. 9, 147 (2020).

    ADS  Google Scholar 

  28. Xia, S. et al. Nonlinear tuning of PT symmetry and non-Hermitian topological states. Science 372, 72–76 (2021).

    ADS  Google Scholar 

  29. Thouless, D. J. Quantization of particle transport. Phys. Rev. B 27, 6083–6087 (1983).

    MathSciNet  ADS  Google Scholar 

  30. Niu, Q. & Thouless, D. Quantised adiabatic charge transport in the presence of substrate disorder and many-body interaction. J. Phys. A Math. Gen. 17, 2453–2462 (1984).

    MathSciNet  MATH  ADS  Google Scholar 

  31. Kraus, Y. E., Lahini, Y., Ringel, Z., Verbin, M. & Zilberberg, O. Topological states and adiabatic pumping in quasicrystals. Phys. Rev. Lett. 109, 106402 (2012).

    ADS  Google Scholar 

  32. Lohse, M., Schweizer, C., Zilberberg, O., Aidelsburger, M. & Bloch, I. A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice. Nat. Phys. 12, 350–354 (2016).

    Google Scholar 

  33. Nakajima, S. et al. Topological Thouless pumping of ultracold fermions. Nat. Phys. 12, 296–300 (2016).

    Google Scholar 

  34. Lohse, M., Schweizer, C., Price, H. M., Zilberberg, O. & Bloch, I. Exploring 4D quantum Hall physics with a 2D topological charge pump. Nature 553, 55–58 (2018).

    ADS  Google Scholar 

  35. Ma, W. et al. Experimental observation of a generalized Thouless pump with a single spin. Phys. Rev. Lett. 120, 120501 (2018).

    ADS  Google Scholar 

  36. Fedorova, Z., Qiu, H., Linden, S. & Kroha, J. Observation of topological transport quantization by dissipation in fast Thouless pumps. Nat. Commun. 11, 3758 (2020).

    ADS  Google Scholar 

  37. Cerjan, A., Wang, M., Huang, S., Chen, K. P. & Rechtsman, M. C. Thouless pumping in disordered photonic systems. Light Sci. Appl. 9, 178 (2020).

    ADS  Google Scholar 

  38. Grinberg, I. H. et al. Robust temporal pumping in a magneto-mechanical topological insulator. Nat. Commun. 11, 974 (2020).

    ADS  Google Scholar 

  39. Jürgensen, M. & Rechtsman, M. C. Chern number governs soliton motion in nonlinear Thouless pumps. Phys. Rev. Lett. 128, 113901 (2022).

    ADS  Google Scholar 

  40. Mostaan, N., Grusdt, F. & Goldman, N. Quantized topological pumping of solitons in nonlinear photonics and ultracold atomic mixtures. Nat. Commun. 13, 5997 (2022).

    ADS  Google Scholar 

  41. Jürgensen, M., Mukherjee, S. & Rechtsman, M. C. Quantized nonlinear Thouless pumping. Nature 596, 63–67 (2021).

    ADS  Google Scholar 

  42. Christodoulides, D. N. & Joseph, R. I. Discrete self-focusing in nonlinear arrays of coupled waveguides. Opt. Lett. 13, 794–796 (1988).

    ADS  Google Scholar 

  43. Eisenberg, H., Silberberg, Y., Morandotti, R., Boyd, A. & Aitchison, J. Discrete spatial optical solitons in waveguide arrays. Phys. Rev. Lett. 81, 3383–3386 (1998).

    ADS  Google Scholar 

  44. Fleischer, J. W., Segev, M., Efremidis, N. K. & Christodoulides, D. N. Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices. Nature 422, 147–150 (2003).

    ADS  Google Scholar 

  45. Christodoulides, D. N., Lederer, F. & Silberberg, Y. Discretizing light behaviour in linear and nonlinear waveguide lattices. Nature 424, 817–823 (2003).

    ADS  Google Scholar 

  46. Kivshar, Y. S. & Agrawal, G. P. Optical Solitons: From Fibers to Photonic Crystals (Academic Press, 2003).

  47. Lederer, F. et al. Discrete solitons in optics. Phys. Rep. 463, 1–126 (2008).

    Google Scholar 

  48. Kevrekidis, P. G. The Discrete Nonlinear Schrödinger Equation: Mathematical Analysis, Numerical Computations and Physical Perspectives Vol. 232 (Springer, 2009).

  49. Dalfovo, F., Giorgini, S., Pitaevskii, L. P. & Stringari, S. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys. 71, 463–512 (1999).

    ADS  Google Scholar 

  50. Pitaevskii, L. & Stringari, S. Bose-Einstein Condensation and Superfluidity Vol. 164 (Oxford Univ. Press, 2016).

  51. Donley, E. A. et al. Dynamics of collapsing and exploding Bose-Einstein condensates. Nature 412, 295–299 (2001).

    ADS  Google Scholar 

  52. Abo-Shaeer, J. R., Raman, C., Vogels, J. M. & Ketterle, W. Observation of vortex lattices in Bose-Einstein condensates. Science 292, 476–479 (2001).

    ADS  Google Scholar 

  53. Deng, H., Weihs, G., Santori, C., Bloch, J. & Yamamoto, Y. Condensation of semiconductor microcavity exciton polaritons. Science 298, 199–202 (2002).

    ADS  Google Scholar 

  54. Kasprzak, J. et al. Bose-Einstein condensation of exciton polaritons. Nature 443, 409–414 (2006).

    ADS  Google Scholar 

  55. Balili, R., Hartwell, V., Snoke, D., Pfeiffer, L. & West, K. Bose-Einstein condensation of microcavity polaritons in a trap. Science 316, 1007–1010 (2007).

    ADS  Google Scholar 

  56. Harper, P. G. Single band motion of conduction electrons in a uniform magnetic field. Proc. Phys. Soc. A 68, 874 (1955).

    MATH  ADS  Google Scholar 

  57. Aubry, S. & André, G. Analyticity breaking and Anderson localization in incommensurate lattices. Ann. Isr. Phys. Soc. 3, 18 (1980).

    MathSciNet  MATH  Google Scholar 

  58. Ke, Y. et al. Topological phase transitions and thouless pumping of light in photonic waveguide arrays. Laser Photon. Rev. 10, 995–1001 (2016).

    ADS  Google Scholar 

  59. Askaryan, G. Effect of the gradient of a strong electromagnetic ray on electrons and atoms. Zhur. Eksptl'. i Teoret. Fiz 42, 1567–1570 (1962).

    Google Scholar 

  60. Chiao, R. Y., Garmire, E. & Townes, C. H. Self-trapping of optical beams. Phys. Rev. Lett. 13, 479–482 (1964).

    ADS  Google Scholar 

  61. Ablowitz, M. J. & Segur, H. Solitons and the Inverse Scattering Transform (SIAM, 1981).

  62. Stegeman, G. I. & Segev, M. Optical spatial solitons and their interactions: universality and diversity. Science 286, 1518–1523 (1999).

    Google Scholar 

  63. Liu, J., Wu, B. & Niu, Q. Nonlinear evolution of quantum states in the adiabatic regime. Phys. Rev. Lett. 90, 170404 (2003).

    ADS  Google Scholar 

  64. Pu, H., Maenner, P., Zhang, W. & Ling, H. Y. Adiabatic condition for nonlinear systems. Phys. Rev. Lett. 98, 050406 (2007).

    MathSciNet  MATH  ADS  Google Scholar 

  65. Vanderbilt, D. Berry Phases in Electronic Structure Theory: Electric Polarization, Orbital Magnetization and Topological Insulators (Cambridge Univ. Press, 2018).

  66. Davis, K. M., Miura, K., Sugimoto, N. & Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 21, 1729–1731 (1996).

    ADS  Google Scholar 

  67. Szameit, A. & Nolte, S. Discrete optics in femtosecond-laser-written photonic structures. J. Phys. B At. Mol. Opt. Phys. 43, 163001 (2010).

    ADS  Google Scholar 

  68. Luo, W.-W., He, A.-L., Wang, Y.-F., Zhou, Y. & Gong, C.-D. Bosonic fractional Chern insulating state at integer fillings in a multiband system. Phys. Rev. B 104, 115126 (2021).

    ADS  Google Scholar 

  69. Schoonderwoerd, L., Pollmann, F. & Möller, G. Interaction-driven plateau transition between integer and fractional Chern insulators. Preprint at https://arxiv.org/abs/1908.00988v2 (2022).

  70. Fu, Q., Wang, P., Kartashov, Y. V., Konotop, V. V. & Ye, F. Nonlinear Thouless pumping: solitons and transport breakdown. Phys. Rev. Lett. 128, 154101 (2022).

    ADS  Google Scholar 

  71. Ams, M., Marshall, G. D., Spence, D. J. & Withford, M. J. Slit beam shaping method for femtosecond laser direct-write fabrication of symmetric waveguides in bulk glasses. Opt. Express 13, 5676–5681 (2005).

    ADS  Google Scholar 

Download references

Acknowledgements

We acknowledge fruitful discussions with S. Gopalakrishnan and S. Vaidya. We further acknowledge the support of the ONR YIP programme under award no. N00014-18-1-2595, ONR-MURI programme N00014-20-1-2325, the AFOSR-MURI programme FA9550-22-1-0339, as well as the Packard Foundation (fellowship no. 2017-66821). C.J. gratefully acknowledges funding from the Alexander von Humboldt Foundation within the Feodor-Lynen Fellowship programme. Numerical calculations were performed on the Pennsylvania State University’s Institute for Computational and Data Sciences’ Roar supercomputer.

Author information

Authors and Affiliations

  1. Department of Physics, The Pennsylvania State University, University Park, PA, USA

    Marius Jürgensen, Sebabrata Mukherjee, Christina Jörg & Mikael C. Rechtsman

  2. Department of Physics, Indian Institute of Science, Bangalore, India

    Sebabrata Mukherjee

Authors
  1. Marius Jürgensen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sebabrata Mukherjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Christina Jörg
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mikael C. Rechtsman
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

M.J. designed, fabricated and cut the devices and carried out all measurements. M.J. characterized the devices with input from C.J. S.M. designed and built the experimental beam shaping and fabrication set-up. The theoretical investigation was carried out by M.J. M.J. and M.C.R. wrote the manuscript, with input from C.J. M.C.R. supervised the project.

Corresponding authors

Correspondence to Marius Jürgensen or Mikael C. Rechtsman.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Yiming Pan and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Properties of solitons.

a. Linear energy bands (grey) for the model described in the main text at Ωz/2π=0.3 together with the nonlinear eigenvalue of a soliton (red) for increasing nonlinearity. Dashed line marks a nonlinear bifurcation point, with a corresponding slope change. b. Wavefunction of the soliton from a. c. Projection of the soliton wavefunction onto the linear energy eigenstates. The eigenstates are sorted via their eigenvalues from bottom (lowest) to top (highest).

Extended Data Fig. 2 Adiabaticity of soliton propagation.

a. Overlap of a numerically propagated soliton with the instantaneous soliton after one pump cycle with period L. b. Same data as a, but plotted as deviation from perfect overlap on a log-log scale confirming the existence of an adiabatic limit. The blue (orange) line depicts to \(gP/{J}^{\max }\)=0.55 (\(gP/{J}^{\max }\)=1.65), which corresponds to the integer (fractionally) pumped soliton in the adiabatic limit.

Extended Data Fig. 3 Linear waveguide characterization.

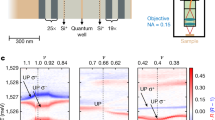
a. Hopping constant J as a function of separation s between waveguides. Each J is calculated via fitting 15 couplers with varying coupling length. Dashed line shows the exponential fit for the coupling function. b. On-site detuning in propagation constant for two waveguides written next to each other as a function of separation s. c. Transmission measurements of a straight waveguide including in- and out-coupling losses. Y-axis is plotted in log scale. The transmission measured for a propagation of ≈ 55 mm is excluded from the exponential fit (dashed line) due to a crack in the sample creating additional losses. The resulting propagation loss is (0.33 ± 0.02)dB/cm.

Extended Data Fig. 4 Nonlinear waveguide characterization.

a. Setup for nonlinear characterization of the waveguides including a pair of gratings (G1 and G2) to stretch and down-chirp the excitation pulse. The output facet is imaged onto a camera and simultaneously focused into a fiber-coupled optical spectrum analyzer (OSA). b. Measured output power for three straight waveguides as a function of the input power showing a linear dependence and hence no nonlinear absorption for input powers less than 6 mW. The threshold indicates the maximum power used in the experiments to prevent damage to the sample. c. Relative intensity in the two waveguides (I1 and I2) of a directional coupler as a function of power. Black lines are a least square fit, resulting in g=0.068/mm per mW input power.

Extended Data Fig. 5 Spectral analysis.

a. Measured normalized spectrum after propagation through a 76.15 mm long, straight waveguide in the uncut sample for increasing input power. The white lines mark the width in which 76% of the intensity is found (corresponding to the full-width-half-maximum of a Gaussian). b,c. Similar to a but spatially resolved and for an array showing fractional pumping. The insets show the waveguide modes at the output facet for increasing input power (from bottom to top). The white rectangle marks the spatial 1/e2 width for which the spectrum is measured.

Extended Data Fig. 6 Triple coupler.

a. Intensity distribution at the output facet for a coupler consisting of three waveguides for low input power. The coupler extends over a length of 5 mm and the top waveguide is excited. b. Normalized output intensities of a triple coupler as a function of the input power. The inset defines the color-coding. Due to the high coupling constant between the waveguides over a short propagation distance of 5 mm, the effects of nonlinearity are negligible.

Extended Data Fig. 7 Verification of soliton’s pumping behavior in the experiment.

a. Amplitude overlap, \({\sum }_{n}| {\Psi }_{n}^{{{{\rm{(Exp.)}}}}}| | {\Psi }_{n}^{{{{\rm{(S)}}}}}|\), between the measured output wavefunction, \({\Psi }_{n}^{{{{\rm{(Exp.)}}}}}\), and the numerically-calculated instantaneous soliton wavefunction, \({\Psi }_{n}^{{{{\rm{(S)}}}}}\), as a function of propagation length for linear propagation (\(gP/{J}^{\max }\)=0.04; shown in blue) and soliton propagation (\(gP/{J}^{\max }\)=2.15; shown in red). b. Center of mass displacement of the experimentally observed soliton and linear propagation (calculated using a higher order norm to suppress linear background effects; see text). Gray line indicates the numerically-calculated displacement of an instantaneous fractionally pumped soliton. c. Experimentally observed center of mass displacement after two periods for increasing input power showing a plateau at high input power. Gray line indicates the expected theoretical displacement of five sites (one unit cell) after two periods for the fractionally pumped soliton. Solid lines with squares show mean values, and shaded areas show one standard deviation for independently measured soliton propagation in eight different unit cells of the same lattice.

Extended Data Fig. 8 Band structure of a 13 site AAH model.

a. Additionally to the 13 linear energy bands (black) the nonlinear eigenvalues of four pumped solitons with \(gP/{J}^{\max }\)=0.04, 0.10, 0.78 and 3.08, which are part of the plateaux in Fig. 4 in the main text, are shown in green, red, blue and yellow, respectively. b Zoom-in onto the central group of three energy bands. c Zoom-in onto the lowest group of five energy bands.

Extended Data Fig. 9 Wannier function positions of a 13 site AAH model.

a. Center of mass position of single-band Wannier functions calculated for each of the 13 bands individually over one period and projected into a single unit cell. The number of windings is equal to the Chern number C of the corresponding band. b-g similar to a but for multi-band Wannier functions in c-g. The position of pumped solitons from the plateaus of Fig. 4 in the main text at nonlinearities \(gP/{J}^{\max }\)=0.04, 0.10, 0.78 and 3.08, are shown in green, red, blue and yellow, respectively.

Supplementary information

Supplementary Information

Supplementary Discussion and Supplementary Fig. 1.

Supplementary Video 1

In Supplementary Animation 1, we compare the measured propagation of the fractionally pumped soliton with numerical tight-binding simulations. The animation complements Fig. 3 and shows the integrated intensity per waveguide for two periods, measured by cutting the sample and observing the intensity distribution at the output facet for increasing input power.

Supplementary Video 2

In Supplementary Animation 2, we show the robustness of the fractionally pumped soliton against bandgap closings (and corresponding Chern number changes) amongst the participating bands. We modify the hopping functions and tune through two topological phase transitions which close the bandgap between the two lowest bands, interchanging their individual Chern numbers from C = {2, −3} to C = {−3, 2} and back to C = {2, −3}. While this process drastically alters the single-band Wannier functions, the multi-band Wannier function of the two lowest bands and therefore also the fractionally pumped soliton do not change their pumping behaviour. In Supplementary Animation 2, we use a five site AAH model with hoppings given by J_n =\left(-0.33-|\cos(\Omega z /2+ \frac{2\pi n}{5})|^{\gamma}\right)/b, where b is an arbitrary length, and we tune γ. The soliton is calculated for gP/Jmax =1.9.

Source data

Source Data Fig. 2

Numerical source data

Source Data Fig. 4

Numerical source data

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jürgensen, M., Mukherjee, S., Jörg, C. et al. Quantized fractional Thouless pumping of solitons. Nat. Phys. 19, 420–426 (2023). https://doi.org/10.1038/s41567-022-01871-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-022-01871-x

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing