Introduction

Nowadays superconducting nanostructures built from InAs nanowires attract huge attention in the field of quantum electronics. Beyond being a versatile platform to investigate the spatial separation of entangled electrons originating from a SC via QDs, namely CPS1,2,3, they are also promising candidates to host such systems as Andreev-qubits4,5,6,7,8 or topologically protected bound states, e.g. Majorana fermions (MF)9,10,11,12,13. Although single-wire circuits have already been realized to study MFs14,15,16,17,18,19,20 and CPS21,22,23,24,25,26, latest theoretical research even predicts non-Abelian anyons with more exotic statistics, so-called parafermions, to appear in devices built from two parallel nanowires27,28,29. It is theorized that Z3 parafermions can arise in a pair of tightly placed wires with a joint SC by exploiting the CAR and the Coulomb interaction2,30,31. As a natural indication of the strong SC-mediated coupling, one might expect the enhancement of CPS in such an arrangement as the distance (δr) between the two points where the split electrons are injected into the parallel QDs can be substantially decreased (see Fig. 1a, b)1,32.

Fig. 1: Device outline.
figure 1

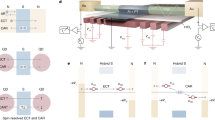
a Concept of a single-nanowire based Cooper pair splitter. Lower bound for δr is the width of the SC with negligible cross-capacitance between the QDs. b Same as panel (a), but in double, parallel nanowires. While δr can be minimized, ULR becomes significant. c High-resolution SEM micrographs of the as-grown nanowires imaged from the opposite side of the Al covering. A TEM image on the top shows the cross-section of the material with the Al connecting the two InAs wires. d False-colored scanning electron microscopy (SEM) image of the device. The epitaxial Al (blue) was etched away from half of the InAs nanowires (brown). Two separate and a shared Ti/Au contacts and side gate electrodes (yellow) were evaporated to control the transport. e Schematic illustration of the measurement setup. The left (red) and right (green) QDs were tuned by VL and VR, respectively, and were biased simultaneously by VSD. The currents in the two arms were measured via I/V converters, yielding the differential conductance GL and GR.

Full size image

Besides CPS is intensively researched in several other platforms, e.g. in graphene-based junctions33,34,35,36, it has been also reported in individual nanowires placed manually next to each other and connected via an ex-situ deposited Al contact37,38. However, hybrid nanostructures became available recently, where double InAs nanowires are grown in close vicinity and are connected by an in-situ evaporated SC Al (see Fig. 1c)39,40,41,42,43,44. The latter property can satisfy a set of strict requirements from the geometry: the direct tunneling between the QDs is prevented45,46, and the SC-nanowire interface becomes high-quality47,48, rendering them a suitable platform for CPS circuits. As a result of the minimal distance of QDs preferred for the CPS in such setups, the inter-dot Coulomb repulsion (ULR) also becomes considerable (see Fig. 1b). This parasitic effect competes with the SC-induced inter-wire transport processes, where two electrons are transmitted through the adjacent QDs. Although previous theoretical works have investigated the mechanism of CPS in parallel double QD systems, they either neglected the impact of the inter-dot capacitance49,50,51, or focused on the regime of strong coupling to the SC (Andreev limit)13,52,53,54,55,56,57,58,59,60,61,62, the opposite of what is desired for CPS1,63.

In this paper, we report a significant CPS signal observed in parallel InAs nanowires with an epitaxial Al layer. We discuss the CPS through a parallel double QD system and estimate the relative reduction of its efficiency in the presence of finite inter-dot Coulomb repulsion energies. Despite the strength of this capacitive coupling being comparable to the superconducting gap (Δ) in our experiments, we report a higher splitting efficiency than in most preceding experiments performed in InAs nanowires. Our findings demonstrate that double nanowires with epitaxial SC are ideal for future applications, where the dominance of crossed Andreev processes is needed27,28,29.

Results

Device outline & setup

The system studied here is illustrated in Fig. 1b–e. Pairs of parallel InAs nanowires were grown in close proximity as discussed in ref. 39 (see panel c). An epitaxial Al layer was deposited in-situ (blue in panels d, e) merging them by covering 2 facets as displayed by a transmission electron microscopy (TEM) image in the top right of Fig. 1c. After transferring a pair of wires to a substrate, the Al was partially removed from them (brown) by using a wet etch method (for details, see Appendix)39. Two normal metal electrodes (Ti/Au, yellow) were formed to the etched segments contacting the wires separately, while a third normal electrode was evaporated on the epitaxial SC (see Fig. 1e) with a distance of ~2 μm measured from the border of the etching. We note that this length exceeds the superconducting coherence length of the Al (ξ). Additional 3-3 side gate electrodes were defined to create electrostatically a QD in each of the wires, thus obtaining parallel SC-QD-N junctions with a joint SC (N stands for normal metal). Low-temperature electronic transport measurements were carried out at a base temperature of 40 mK.

Tunnel barriers were formed by adjusting the voltage on the outer side gates. If the coupling of the QDs is stronger to the SC than to the normal leads, sub-gap states can be formed and one enters the Andreev limit13,52,53,54,55,56,58,61,62. In our case, the tunnel barriers were set such that the opposite limit was reached, where the normal leads were coupled strongly. This allowed the QDs to be emptied rapidly without blocking the transport, hence making it suitable to investigate CPS1,63. The middle finger gate electrodes served as plunger gates to tune the level position of the left (red) and right (green) QDs by VL and VR, respectively (see Fig. 1e). Differential conductance GL = dIL/dVAC and GR = dIR/dVAC through the left and right QDs were recorded on the normal contacts biased by VSD applied on the offset inputs of home-built I/V converters. With this geometry, we minimized δr in order to boost the superconducting inter-dot correlations as suggested in refs. 1,32, since the CPS current (ΔI) is suppressed as:

$${{\Delta }}I\propto \exp \{-2\delta r/\pi \xi \},$$
(1)

however, we also introduced a finite ULR at the same time, as shown in Fig. 1b.

Experiments

In the following, we discuss the spectrum of the created double QD system. Figure 2a, b show the zero-bias conductance of the left and right QDs, respectively, as a function of the two plunger gate voltages in the normal state reached by B = 250 mT out-of-plane magnetic field. The finite slopes of the lines are attributed to the capacitance between the left (right) plunger gate and the right (left) QD. The resonance lines of each QD shift in the phase diagram when the other one is being charged (or discharged) due to the significant inter-dot Coulomb repulsion, resulting in an effective gating and exhibiting a honeycomb pattern, which is well-known for capacitively coupled double QDs64. Figure 2c, d show normal-state finite-bias spectroscopy of the left and right QDs performed along the white and gray dotted line in Fig. 2a, b, while Fig. 2e, f show the same measurements in the superconducting state (B = 0). The charging energies of the left and right QDs were extracted from the size of the Coulomb-diamonds as UL = 0.9 meV and UR = 0.7 meV, while the total couplings were estimated from the level broadenings as ΓL ≈ 0.28 meV and ΓR ≈ 0.45 meV, respectively. Here ΓL(R) = ΓSL(R) + ΓNL(R) and ΓSL(R) describes the tunnel rate between the SC and the left(right) QD, while ΓNL(R) is the tunnel rate between the left (right) QD and the normal lead. The strength of the inter-dot Coulomb repulsion was found to be ULR = 0.15 meV estimated from the relative shift of the resonance lines in Fig. 2a, b64. In Fig. 2e, f the Coulomb resonances split up at zero bias and a soft gap opens with 2Δ energy in the excitation spectra (with Δ = 0.15 meV), typical for SC-QD-N junctions. The tip of the diamonds also shift in gate voltage and the lack of sub-gap states confirms the weak coupling towards the SC (ΓSL(R) ≪ ΓNL(R)), needed for CPS experiments.

Fig. 2: QD characterization.
figure 2

a, b Zero-bias stability maps of the left and right QDs in the normal state. Finite capacitance between the plunger gates to the opposite QDs with the strong inter-dot Coulomb repulsion establishes a honeycomb structure in the phase diagram. c, d Bias spectroscopy of the left and right QDs in the normal state and e, f in the superconducting state along the white and gray dotted lines in panels (a, b). ULR = 0.15 meV was read off from the phase diagram, while charging energies of the left and right QDs were extracted as UL = 0.9 meV and UR = 0.7 meV, respectively, with Δ = 0.15 meV from the Coulomb-blockade spectroscopy. The couplings were estimated to be ΓL ≈ 0.28 meV and ΓR ≈ 0.45 meV.

Full size image

Let us now explore the zero-bias conductance of the QDs from Fig. 2a, b, but in the superconducting state. The corresponding charge stability maps are shown in Fig. 3a, b. Here the conductance of both QDs is smaller globally compared to Fig. 2a, b, but non-zero due to the presence of the soft gap. In contrast to the normal-state data where the capacitive cross-talk yields minima at the intersections of the left and right QD resonances, in the superconducting state, maxima develop instead. These are manifested in Fig. 3b by the yellow spots at the shifting resonance lines. To prove that CPS takes place in our system and to quantify its efficiency, we focus on the evolution of the signal amplitudes along single resonance lines. In Fig. 3c GL and GR are plotted along a resonance of the right QD, whose trace is depicted with the blue dashed line in Fig. 3a, b. The red curve shows the resonances of the left QD, and we call this signal "local", whereas the green one shows the changes in the conductance of the right QD as a function of VL, hence we denote this as the "non-local" signal. Although GR is always maximal along this cut, well-pronounced peaks emerge when the left QD is also brought to resonance. Similarly, in Fig. 3d, where the roles of QDs are interchanged, GL and GR are demonstrated along the pink dashed line from Fig. 3a, b. Here one can see a significant increase in the left QD signal when the right QD becomes resonant as well. E.g. the non-local peaks at VL = 3.24 V and VR = 0.07 V can be recognized in both QD signals in Fig. 3c, d with the equal height of ΔG indicated by the black arrows. These non-local maxima vanish by switching off the superconductivity as shown in Fig. 3e, f, where the same analysis was carried out as in Fig. 3c, d but in the normal state along the blue and pink dotted lines in Fig. 2a, b. In the absence of superconductivity, the overall conductivity increases, and the non-local peaks are replaced by dips. These features are robust along each resonance (for additional data, see Supplementary Note 1). We emphasize that the dips are much deeper than what is expected from resistive cross-talk introduced in ref. 21, and they are caused by the finite inter-dot capacitance, which penalizes the simultaneous electron occupation of the adjacent QDs. The strong positive correlation only existing in the superconducting state demonstrates the presence of robust CPS.

Fig. 3: CPS validation.
figure 3

a, b Same gate stability maps as in Fig. 2a, b, but in the superconducting state. The white and gray arrows show the spots with the maximal splitting efficiency and maximal visibility of the non-local signal, respectively. c Conductance along a selected resonance of the right QD indicated by the blue dashed line in panels (a, b). There is a strong positive correlation between GL and GR. d Similar cut to panel (c), but along a resonance of the left QD shown by the pink dashed line in panels (a, b). The peaks at VL = 3.24 V match the one at VR = 0.07 V in panel (c) with the same amplitude of ΔG. e, f Normal state data of the corresponding cuts in panels (c, d) (taken along the pink and blue dotted lines in Fig. 2a, b). Once the superconductivity is suppressed by external magnetic field, negative correlations overtake the non-local peaks arising from the non-negligible ULR.

Full size image

The CPS efficiency can be defined as s = 2ΔG/(GL + GR), while visibility of the non-local signal in the left (right) QD is ηL(R) = ΔG/GL(R), where ΔG is the non-local signal amplitude equal in the two wires (see Fig. 3c, d)21,24,37,46. We estimated the maximal and average CPS efficiency as \({s}_{\max }=\) 29–36% (see the white arrow in Fig. 3a, b) and \(\overline{s}=\) 19–28% in the investigated gate range, respectively. The maximal visibility was found to be \({\eta }_{{{{\rm{L,max}}}}}=\) 40–49% and \({\eta }_{{{{\rm{R,max}}}}}=\) 29–40% (see the gray arrow in Fig. 3a, b). The lower bounds of the given ranges are derived as ΔG being measured from the baseline of the resonances. More realistic estimates (used here as upper bounds) are calculated by considering the relative reduction of the conductance usually reaching 15% (see Fig. 3e, f), which is always present in the system as it comes from the capacitive coupling. In this case, the CPS signals are estimated by the sum of the previously described ΔG and the expected depth of the dips in the QD with smaller average conductance in the superconducting state. Here the condition of the non-local signals being equal in GL and GR is still satisfied, however, these numbers could even increase, if one takes into account higher-order processes, where the electrons of a Cooper pair split into different QDs finally leave to the same electrode24,45. In the following, we explore the relative reduction of these quantities caused by the Coulomb interaction between the QDs.

Discussion

A finite ULR is expected to quench the CPS as it penalizes transport processes where both QDs are being charged simultaneously. To confirm this assumption and to quantify this effect, we developed a rate equation model to calculate the relative CPS currents in parallel QDs at different electron occupations.

The QDs are treated as single sites in the frame of the Anderson model with δr = 0. We use the notation \(\left|m,n\right\rangle\) for \({\left|m\right\rangle }_{{{{\rm{L}}}}}\otimes {\left|n\right\rangle }_{{{{\rm{R}}}}}\) describing the ground state electron filling of the left and right QDs, where m, n = {0, ↑, ↓, 2}. The SC and the normal leads are handled by BCS density of states and Fermi distributions, respectively. All tunnel couplings are assumed to be weak compared to the governing energy scales (UL(R), Δ)50, and the transport is entirely described by transition rates determined by 4th order perturbation theory with Fermi’s golden rule. The net current in the left (right) lead is obtained by solving the classical master equation in the stationary limit (for further details, see Supplementary Note 3).

Among the various transport mechanisms available in the system we distinguish local pair tunneling (LPT) and CPS in the calculations. A sequence of electron tunnelings is treated as LPT if the electrons constituting the Cooper pair leave the SC to the same QD, while the transport is considered to be CPS if the split electrons exit to separate QDs. One example for each of them is demonstrated in Fig. 4a where the order of the events in the sequence is indicated by black arrows and numbers. In both processes the initial and final states have the \(\left|\uparrow ,0\right\rangle\) character, however, electrons with opposite spins arrive in the same leads at the end of a LPT, while they appear in separate arms in case of CPS (for a detailed discussion see Supplementary Note 3).

Fig. 4: Transport modeling.
figure 4

a A possible sequence of LPT and CPS. The arrows with the numbers indicate the event order in the sequence. Electrons in gray symbolize the initial occupations, while the purple ones belong to the final states. b Sketched phase diagram of the honeycomb presenting the border of ground state occupations of both QDs simultaneously. By crossing the red (green) line, the electron number is changed on the left (right) QD. c ULR/U dependence of s calculated in different points of the stability diagram, indicated by markers in panel (b). While a decreasing tendency of the CPS contribution to the total current can be observed throughout the phase diagram, the efficiency is maximal in the middle of the \(\left|1,0\right\rangle\) and \(\left|0,1\right\rangle\) degeneracy lines.

Full size image

Intuitively, one expects the CPS efficiency to be maximal when both QDs are close to their resonances1. This condition is satisfied in the vicinity of the degeneracy line of the \(\left|1,0\right\rangle\) and \(\left|0,1\right\rangle\) sectors in the phase diagram, i.e. at −1 < ϵL/ULR = ϵR/ULR < 0 on-site energy settings (brown line connecting the triple points in Fig. 4b). Therefore we studied the CPS efficiency s = 2ΔI/(IL + IR) as a function of the inter-dot Coulomb repulsion at different locations in the stability map assigned by the markers in Fig. 4b, which are plotted in Fig. 4c. For simplicity, the charging energies were chosen as UL = UR = U = 1 meV and Δ = 0.2 meV has been used.

As visible in Fig. 4c, s is significantly higher along the degeneracy line of the \(\left|1,0\right\rangle\) and \(\left|0,1\right\rangle\) sectors (pink triangle, blue square, yellow diamond) than anywhere else in the stability diagram. and maximal at ϵL/ULR = ϵR/ULR = −0.5, i.e. in the middle of the degeneracy line (blue square). This result is consistent with our experimental data where the non-local peaks were positioned to the center of the crossing resonance lines. By moving towards either of the triple points (pink triangle at ϵL/ULR = ϵR/ULR = −0.8), s decreases slightly. This small effect originates from the fact any of the CPS cycles that involves both the \(\left|0,0\right\rangle\) and the \(\left|1,1\right\rangle\) configurations as intermediate states (see the CPS process step (1) and (3) depicted in Fig. 4a), thereby being penalized by ~ULR. Obviously, by increasing ULR the triple points separate further, hence suppressing s. We note that the calculations were performed at fixed ϵL(R)/ULR ratios compensating the change of the length of the brown degeneracy line in Fig. 4b. Once one of the QDs is detuned from the resonance (at the gray circle and the green triangle with fixed ϵL(R)), s drops significantly in accordance with the expectations as LPT starts to dominate the transport. Altogether, ULR ≈ Δ < 0.2 meV relevant for our experimental values, the reduction of s does not exceed 10% compared to the non-interacting case. We note that similar results can be obtained at other on-site energy settings (e.g. in the vicinity of the \(\left|1,1\right\rangle ,\left|2,1\right\rangle ,\left|1,2\right\rangle\) and \(\left|2,1\right\rangle ,\left|1,2\right\rangle ,\left|2,2\right\rangle\) triple points) due to the symmetry of the charge stability diagram.

As a simple analysis, one can derive the maximal efficiency attainable in single-nanowire-based CPS by assuming the typical values of δr ≈ 300 nm (see Fig. 1a) and ULR = 0 (I.), and compare it to the calculation performed ULR = 0.15 meV by assuming δr = 30 nm, reasonable for our setup (II., see Fig. 1a). According to Eq. (1), in the former case, \({s}_{\max }^{{{{\rm{I.}}}}}\approx 82\)%, while in the latter one \({s}_{\max }^{{{{\rm{II.}}}}}\approx 89\)% in principle. By using these values, the geometry exhibiting a minimal δr, yet a finite ULR turns out to be beneficial regarding the CPS efficiency. Naively one can argue it as ULR ∝ 1/δr while s decays exponentially in δr as outlined in Eq. (1). This consideration with the relatively high CPS efficiency reported here in spite of the parasitic inter-dot Coulomb repulsion confirms the advantageous application of parallel InAs nanowires in future SC-semiconductor hybrids.

In summary, we have demonstrated significant Cooper pair splitting signals realized in parallel InAs nanowires connected by an epitaxial Al shell. The behavior of the coupled parallel SC-QD-N junctions was analyzed by spectroscopic measurements in both the superconducting and normal states. Owing to the geometrical properties, strong capacitive interaction was found between the QDs whose effect on the CPS was thoroughly studied. Due to the high-quality interface between the SC and semiconductor and the controlled QD formation, \({s}_{\max }=\) 29–36% CPS efficiency was achieved larger than previously reported in parallel-wire-based experiments, which lacked these features37. Our theoretical modeling also proved that regarding \({s}_{\max }\), the small spatial separation of QDs outgrow the drawbacks of the inter-dot Coulomb repulsion. The strong CAR makes the double-wire system with epitaxial shell a promising platform to develop quantum circuits designed to realize Majorana bound states14 or such exotic states as parafermions27.

Methods

Device fabrication

InAs nanowires were grown by MBE in the wurtzite phase along the 〈0001〉 direction catalyzed by Au. The pattern of the pre-defined Au droplets allowed to control the geometrical properties of the proposed parallel nanowires, including the diameter, distance, and the corresponding alignment of the cross-sections39. The 20-nm-thick Al shell (covering 2 facets) was evaporated at low temperature in-situ providing epitaxial, oxide-free layers. The evaporation on such a pair of adjacent nanowires resulted in the merging by the Al. Nanowires with ~80 nm diameter, ~4 μm length, and ~200 nm seed separation were deposited on a p-doped Si wafer capped with 290 nm thick SiO2 layer by using an optical transfer microscope with micromanipulators. The Al shell was partially removed by the means of wet chemical etching. A coated MMA/MAA EL-6 double-layer performed as a masking layer, in which designed windows were opened with EBL allowing the MF-321 selective developer to access the Al (45 s). The etching was followed by a careful localization of the wires with high-resolution SEM. The contact electrodes were installed in a separate EBL step with a thicker PMMA resist (300 nm), where the sample was exposed to RF Ar milling in the evaporator chamber to remove the native oxide of both the Al and InAs. The process was followed by the metallization of Ti/Au (10/80 nm) with electron beam evaporation without breaking the vacuum. In a second EBL step, the side gate electrodes were created by using thinner PMMA resist (100 nm) and depositing Ti/Au (10/25 nm).

Measurements

Low-temperature characterization was carried out in a Leiden Cryogenics dry dilution refrigerator with a base temperature of 40 mK. Transport measurements were performed with standard lock-in technique by applying 10 μV AC signal at 137 Hz on the shared SC electrode, whereas the differential conductance of the nanowires was recorded separately via home-built I/V converters. DC bias was adjusted by the offset of the I/V converters. Out-of-plane magnetic field was realized by a superconducting magnet. The QDs were formed by the outer finger gate electrodes with VTL = −3.5 V, VBL = −1.6 V, \({V}_{{{{\rm{TR}}}}}=-6.5\,\)V, and VBR = 0 V values, where T(B) stands for top (bottom) and L(R) stands for left (right) labeling them by following the arrangement visible in Fig. 1d. Both large side gates on the top in Fig. 1d were set to VG = −2 V to slightly tune the electron density in the nanowire segments covered by the Al shell.