Multipartite entanglement of billions of motional atoms heralded by single photon

Abstract

Quantum theory does not prevent entanglement from being created and observed in macroscopic physical systems, in reality however, the accessible scale of entanglement is still very limited due to decoherence effects. Recently, entanglement has been observed among atoms from thousands to millions levels in extremely low-temperature and well isolated systems. Here, we create multipartite entanglement of billions of motional atoms in a quantum memory at room temperature and certify the genuine entanglement via M-separability witness associated with photon statistics. The information contained in a single photon is found strongly correlated with the excitation shared by the motional atoms, which intrinsically address the large system and therefore stimulate the multipartite entanglement. Remarkably, our heralded and quantum memory built-in entanglement generation allows us to directly observe the dynamic evolution of entanglement depth and further to reveal the effects of decoherence. Our results verify the existence of genuine multipartite entanglement among billions of motional atoms at ambient conditions, significantly extending the boundary of the accessible scale of entanglement.

Introduction

Quantum technologies, incorporating quantum entanglement¹ into communication^2,3, simulation^4,5,6,7,8, computation^9,10,11, and metrology¹², exert great advantages beyond classical approaches. For a large-scale multipartite entangled system, the dimension of Hilbert space will be exponentially expanded as the number of entangled particles increases, which inspires novel approaches of quantum computing or direct simulation for classically intractable problems^3,11. The ability to access large-scale and more practical multipartite entanglement has been regarded as a benchmark for quantum information processing, like the road map towards quantum supremacy¹³. However, decoherence resulting from strong internal interactions and coupling with the environment makes entanglement fragile, which limits the expansion of the scale of multipartite entanglement, especially reaching the level of macroscopic physical systems.

So far, significant experimental progresses have been made in realizing different classes of multipartite entanglement in different artificially engineered quantum systems. Greenberger-Horne-Zeilinger state, a well-known maximally entanglement state, has already been generated at a scale of up to 12 qubits in superconducting systems¹⁴, 18 qubits in photonic systems¹⁵, and 20 qubits in ions systems¹⁶. The exponentially low efficiency in simultaneously detecting many particles restricts its achievable scale. An interesting way to enhance the collective correlation is to create the twin Fock entanglement state in a Bose-Einstein condensate (BEC) system through quantum phase transitions¹⁷. W state is another representative multipartite entanglement with only one excitation shared by all particles. The requirement of detecting single excitation for W state is free from the exponential inefficiency of coincidence measurement, which makes it more easily achieved at a large-scale, especially in atomic ensembles^18,19,20,21.

The achieved large-scale entanglement states, however, have to be prepared and detected in the systems that are maintained at extremely low temperatures and well isolated with an environment to eliminate decoherence effects. The decoherence and noise-induced by the motion and collision of room-temperature atoms are apparently harmful^22,23, and therefore were avoided in purpose in previous endeavors of observing large-scale entanglement. Recently, the Duan-Lukin-Cirac-Zoller (DLCZ) protocol operating in a far-off-resonance configuration has been found capable of being operated well in room-temperature conditions. This far-off-resonance protocol well eliminates the collision-induced fluorescence noise and endows a large memory bandwidth, which obviously solves the difficulties that the EIT and near off-resonance Raman schemes meet in hot vapor cells.^24,25,26,27. Though being challenging, it would be more desirable to explore whether large-scale entanglement can exist in ambient conditions and be shared by more motional atoms, not only for the fundamental interest of probing the boundary of quantum to classical transition, but also for future real-life quantum technologies.

Here, we experimentally demonstrate a multipartite entanglement of billions of motional atoms in a room-temperature quantum memory. The multipartite entanglement W state in a hot atomic vapor cell is heralded by registering a Stokes photon derived from the far-off-resonance spontaneous Raman scattering (SRS). In order to certify and quantify the scale of entanglement, we convert the shared excitation of W state into an anti-Stokes photon by applying another interrogation pulse, and reveal an entanglement depth up to billions of atoms by the witness constructed with the correlated photon statistics. The far-off-resonance configuration endorses the broadband feature allowing it to be operated at a high data rate. Furthermore, our heralded and quantum memory built-in fashion of entanglement generation allows us to directly observe the dynamic evolution of entanglement depth in a dissipative environment.

Results

Creating W states among atoms

To herald multipartite entanglement W state, we adopt the SRS regime as proposed in the Duan-Lukin-Cirac-Zoller (DLCZ) protocol originally aiming at realizing applicable quantum repeaters²⁴. However, we have to conceive a far-off-resonance scheme to avoid the huge fluorescence noise in room-temperature atomic ensemble^25,26,27, which does not exist in cold ensembles and diamonds^28,29. The energy levels of the Λ-type configuration are shown in Fig. 1a. This process will generate the correlated photon-atoms pair, which can be expressed as²⁹

$$\left|{\psi }_{s}\right\rangle =\left[1+{\varepsilon }_{s}{S}^{{\dagger} }{a}^{{\dagger} }\right]\left|vac\right\rangle$$

(1)

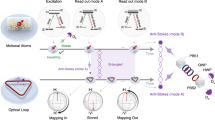
where ∣ε_s∣² is the excitation probability of Stokes photon, $\left|vac\right\rangle =\left|va{c}_{opt}\right\rangle \bigotimes \left|va{c}_{ato}\right\rangle$ is the initial product state of a photon-atoms system, S and a are the annihilation operators of spin-wave and Stokes photon, respectively. Here, we set the intensity of the control light pulse so weak that the excitation probability ∣ε_s∣² is much smaller than unity. Therefore, we can ignore the higher-order terms in creating of $\left|{\psi }_{s}\right\rangle$ with extremely small probability^24,30. With the creation operators acting on the initial state of an atomic ensemble, the W state is written as^22,26$\left|{W}_{1}\right\rangle =\frac{1}{\sqrt{N}}\mathop{\sum }\limits_{j=1}^{N}{e}^{i{{\Delta }}\overrightarrow{k}\cdot {\overrightarrow{r}}_{j}}\left|{g}_{1}{g}_{2}...{s}_{j}...{g}_{N}\right\rangle$, where N is the number of involving atoms, ${{\Delta }}\overrightarrow{k}$ is the wave vector of spin-wave, ${\overrightarrow{r}}_{j}$ is the position vector of j_th excited atom. This generating process of entanglement is shown in Fig. 1b, and the W state can be heralded through the detection of one scattering Stokes photon. $\left|{W}_{1}\right\rangle$ contains only one excitation shared by all motional atoms illustrated in Fig. 1c, where every atom posesses the equal probability of being excited with spin up.

Fig. 1: The schematic diagram of creation and verification of multipartite entanglement.

a The energy levels of creating and verifying W state. Solid lines represent three-level Λ-type configuration of atoms, two ground states label $\left|g\right\rangle$ (6S_1/2, F = 3) with electronic spin down and $\left|s\right\rangle$ (6S_1/2, F = 4) with electronic spin up, which are hyperfine ground states of cesium atoms (splitting is Δg = 9.2 GHz); excited state labels $\left|{{{\rm{e}}}}\right\rangle$ ($6{P}_{3/2},{F}^{\prime}=2,3,4,5$). The shaded area between energy levels represents broad virtual energy levels induced by the short pump and probe laser pulse (2 ns). b The experimental scheme of creating and certifying the multipartite entanglement. The Hanbury Brown–Twiss interferometer is used for analyzing the statistics of the correlated Stokes and anti-Stokes photons, which can further reveal the information of entanglement depth. c The dashed red arrows means that every atom has an equal probability to be spin up or down, which is the main feature of the W state. d The decoherence effects may change the structure of the multipartite entanglement. We take the two excitations event as examples to show the evolution of entanglement depth. The distributed cesium atoms with different colors illustrate the entanglement distribution with several subgroups. The set of same-colored atoms is genuine multipartite entanglement, while two sets with different colors do not have the relationship of entanglement.

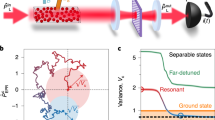
It is inevitable that the SRS in the generating process may produce high-order excitations with a comparably low probability, and such terms would change the structure of our desired multipartite entanglement. The entangled ensemble with the two-excitation events can be generally expressed as $\left|{W}_{2}\right\rangle =\sqrt{\frac{2}{N(N-1)}}\mathop{\sum }\limits_{i < j}^{N}{e}^{i{{\Delta }}\overrightarrow{k}\cdot \left({\overrightarrow{r}}_{j}+{\overrightarrow{r}}_{i}\right)}\left|{g}_{1}{g}_{2}...{s}_{i}...{s}_{j}...{g}_{N}\right\rangle$, and higher-order events have negligible contributions. To certify and qualify the W state, we need to apply another optical probe pulse to convert the shared single excitation in the atomic ensemble into an anti-Stokes photon, as shown in Fig. 1a, b. In order to obtain the information of entanglement depth, we analyze the photon number statistics of the correlated Stokes and anti-Stokes photons via a Hanbury Brown–Twiss interferometer (as Fig. 1b shows and more experimental details see Methods). Due to the decoherence effects, as Fig. 1d shows, the atomic ensemble with high-order excitations will evolve to several subgroups, where each part shares single excitation²¹. Suppose that the whole atomic ensemble is in a pure state, containing M separable parts, which can be expressed in a product form $\left|\psi \right\rangle =\left|{\psi }_{1}\right\rangle \otimes \left|{\psi }_{2}\right\rangle ...\otimes \left|{\psi }_{M}\right\rangle$, where M is the number of separable subgroups, $\left|{\psi }_{i}\right\rangle (i=1,...,M)$ represents each separable group that may contain individual multipartite entanglement, while different subgroups are independent of the others. For an extremely large-scale multipartite entanglement, it is convenient to adopt the concept of entanglement depth to characterize its scale information. Here, we can define entanglement depth as D = N/M²¹, which represents the smallest number of genuinely entangled particles among the subgroups, and N is the number of total atoms participating in the interaction.

Verifying the W states by witness

In order to quantify the multipartite entanglement, we adopt the entanglement witness compatible with photon number statistics of the correlated photons pair. Such witness is efficient especially when the vacuum component of the state is dominant²¹. For a given M value, we ought to determine the lower bound of the entanglement state with D particles entangled (see Methods). The witness operator can be expressed as

$${\omega }^{M}=\left|{W}_{2}\right\rangle \left\langle {W}_{2}\right|-{p}_{2}^{bound}({p}_{1},M)$$

(2)

where the two key parameters p₁ and p₂ are projective probabilities in the forms of ${\left|\left\langle {W}_{1}| \psi \right\rangle \right|}^{2}$, ${\left|\left\langle {W}_{2}| \psi \right\rangle \right|}^{2}$, and ${p}_{2}^{bound}({p}_{1},M)$ stands for the theoretical minimal value of p₂ under the condition of fixed p₁ and M value. For the density matrix ρ of experimental state, tr(ρω^M) < 0 means that the entanglement depth is at least D = N/M. In actual experiments, p₁ should be defined as the conditional probability of detecting a correlated anti-Stokes photon with a heralding forward Stokes photon, and the probability p₂ stands for the probability of two excitation events, which is deduced by the autocorrelation function ${g}_{A{S}_{1}\cdot A{S}_{2}| S}^{(2)}=2{p}_{2}/{p}_{1}^{2}$ measured by a Hanbury Brown–Twiss interferometer.

The decoherence effects can be revealed by the observation of entanglement depth’s evolution via adjusting the delay of optical probe pulse in our quantum memory built-in configuration. The p₁ can be influenced by the retrieval efficiency of quantum memory, the photon loss of the channels and detectors. Therefore, the final experimental data should be handled as the following two stages: the raw measured data and the processed data after subtracting the loss of the channels and detectors. The latter reflects the genuine entanglement state at the moment just after applying the probe pulse. The M values of entanglement state evolving with storage time are shown in Fig. 2, where the energy of the light pulses is 225 pJ. The data point below the boundary curve of fixed M value indicates that there is an entanglement depth at least N/M. Our experimental data show that the number of entanglement subgroups increases as the memory time elapsing, i.e. the decoherence effects caused by the thermal motions of atoms^22,26 will tremendously influence the structure of entanglement, which is consistent with the physical picture depicted in Fig. 1d.

Fig. 2: Dynamical evolution of the multipartite entanglement.

The verification results of witness and dynamical evolution of M values with different storage times in 30, 120, 300, 450, 900, and 1200 ns from right to left. The corresponding different M values of theoretical lower bound curves of witness are 10–10⁶ from right to left. The M values for experimental data are 5, 6, 10, 14, 92, and 1000 in the right subgraph. According to the error bars from the statistical data, we can deliver the upper bound of the M values as $\left[5,6,12,16,130,+\infty \right]$, and the lower bound as $\left[5,5,9,13,90,323\right]$. Here, the + ∞ of M values represents the approach to the classical bound. Error bars are derived by the Poisson distribution of photon number statistics from avalanche photodiodes.

During the process of verifying the existence of entanglement, the collective enhancement effect contributes to the transducing of Stokes photon due to the phase coherence of W state²⁴. The variation of p₁ with the delay of the probe pulse is shown in Fig. 3a. Due to the decoherence of phase mainly resulting from the motions of warm atoms, the effect of collective enhancement becomes deteriorative, which results in the exponential decay of p₁. What is more, we measure the cross-correlation between the correlated photons and the autocorrelation of the retrieved anti-Stokes photon as shown in Fig. 3b. The degrade of quantum correlation and single photon characteristic implies the variation of the structure of multipartite entanglement according to the relation of p₂ and ${g}_{A{S}_{1}\cdot A{S}_{2}| S}^{(2)}$ (see Methods), which are consistent with the deduced M values in Fig. 2. Our results well exhibit the quantum-to-classical transition in multipartite entanglement of billions of motional atoms heralded by a single photon.

Fig. 3: Decoherence of the multipartite entanglement.

a The variation of p₁ probabilities. b The cross-correlation ${g}_{S-AS}^{(2)}$ between correlated Stokes and anti-Stokes photons is on the left side (as pink dots show); the autocorrelation ${g}_{A{S}_{1}-A{S}_{2}| S}^{(2)}$ of the retrieved anti-Stokes photon heralded by the Stokes photon is on the right side (as blue dots show), which approaches 1 as the storage time increases. Error bars are derived by the Poisson distribution of photon number statistics from avalanche photodiodes. c The evolution of entanglement depth varies with the storage time of quantum memory. According to the error bars of M values in Fig. 2, we can calculate the variance of evaluating the entanglement depth. The entanglement depth with the memory time from 30–1200 ns are $\left[1.77,1.47,0.88,0.63,0.09,0.009\right]\times 1{0}^{9}$, while the lower bounds are $\left[1.77,1.47,0.74,0.55,0.07,0\right]\times 1{0}^{9}$. The lower bounds of entanglement depth during the memory time from 30–900 ns with confidence 3σ = 99.7% are listed as $\left[1.77,0.59,0.35,0.35,0.01\right]\times 1{0}^{9}$. The variance of the entanglement depth with the memory time of 1200 ns has approached the classical bound, and we can't deliver its reasonable confidence evaluation.

From another perspective, we can demonstrate how the entanglement depth varies with the delay time. In order to determine the information of entanglement depth, the number of total cesium atoms involved in the interaction is the key parameter that should be measured precisely. The atomic density can be obtained by fitting the measured transmission rate of light with different frequencies according to the absorption model, and the total atomic number is evaluated by the coherence analysis of the collective enhancement effect according to the collection optics (see Methods). The results show that there are nearly at least 1.77 billion motional atoms sharing one excitation constituting the W state. As is shown in Fig. 3c, despite the fast decrease of entanglement depth resulting from the increased noise and the destructive effects of decoherence, there is still considerable entanglement depth in the warm atomic ensemble after storing for microseconds level.

It is also accessible to manipulate the size of the large-scale entanglement state in the macroscopic ensemble by changing our experimental parameters. What dominantly influences the p₁ probability in our experiment is the energy of the addressing light pulse, which determines the excitation probability of the Stokes photon during the SRS process. The M values of multipartite entanglement created by different pulse energies, 115.5 pJ, 225 pJ, 330 pJ respectively, are shown in Fig. 4a. The dependence of entanglement depth on excitation probability, the light pulse energy is also analyzed and shown in Fig. 4b. The results show that the stronger light pulse energy has a higher p₁ probability because of the higher converting efficiency of the W state, but has a smaller M value, which indicates that the structure of multipartite entanglement has not been deteriorated by noise. Limited by the power of our laser set-up, we can’t further explore the qualitative relationship between the entanglement depth and the pulse energy. Based on the fact that the cross-correlation between Stokes and anti-Stokes photons would decrease when the pulse energy becomes stronger²⁶, we may deduce that the entanglement depth would also meet the turning point because of the increasing noise level.

Fig. 4: Measured entanglement depth with different excitation probabilities.

a The M values with different excitation probabilities are 14, 5, 5, and the corresponding energy are E₁ = 115.5 pJ, E₂ = 225 pJ, E₃ = 330 pJ. The uncertainty for the M value of E₁ is mainly derived from the error bar of p₂ with the upper bound of 15 and the lower bound of 10. The time interval between creation and verification light pulse is 30 ns. Error bars are derived by the Poisson distribution of photon number statistics from avalanche photodiodes. b The visualized entanglement depth for comparison with different excitation probabilities. The red dots represent the relations of the excitation probability and pulse energy, and the size of the circle taking the red dot as center stands for the scale of entanglement depth. According to the aforementioned definition of entanglement depth, it determines the smallest number of genuinely entangled particles among the M subgroups, which only delivers a lower bound of the genuine entanglement scale. Thus, it is reasonable that the same lower bound of entanglement depth is observed with different excitation probabilities.

Discussion

In summary, we have experimentally demonstrated a multipartite entanglement of billions of motional atoms heralded by a single photon. With the quantum memory built-in and broadband capacities, we have efficiently displayed the dynamical evolution of entanglement depth and decoherence effects. Remarkably, this certifies the feasibility for testing quantum-to-classical transition with multipartite entanglement at the ambient environment, which is prominently different from the other platforms with rigorous conditions. Our work has certified that quantum entanglement can be observed in a macroscopic room-temperature atomic ensemble with motional atoms and demonstrated the accessibility of feasible manipulations of entanglement depth, which expands the bound of operating large-scale multipartite entanglement and may stimulate a wide spectrum of applications for the future quantum information science and technologies.

Creating a large-scale multipartite entanglement of more atoms is possible, a larger beam waist and stronger energy of light pulse will be helpful with the prerequisite of well-controlled levels of noise. What’s more, the larger beam waist can mitigate the detrimental effect of decoherence brought by the thermal motions of atoms, since there is a broader space to prevent warm atoms from escaping from the interaction region, which leads to a longer lifetime of multipartite entanglement. Recent works also show that the anti-relaxation coating of vapor cells will preserve the coherence for longer lifetime^31,32, which may be beneficial for improving the maintenance of the heralded multipartite entanglement. Remarkably, recent proposals and experimental developments about transferring the single collective excitation of electronic spins to noble-gas nuclear spins by spin-exchange regime may exceedingly prolong the lifetime of the W state even up to several hours^33,34.

The W state with phase information encoded in billions of atoms exists in the form of a spin-wave, which resembles tremendous networked quantum sensors with an entanglement between each element. The phase information of spin-wave is not only related to the position information of motional atoms, but also sensitive to some other physical parameters related to atomic internal states, like magnetic field³⁵, which makes the W state become a promising candidate for quantum sensing. Interestingly, the W state is also robust for the purpose of metrology, because the remaining particles are still entangled while one particle is traced out. Furthermore, the multipartite entanglement constructed between these quantum sensors may significantly enhance the precision of multiparameter estimation³⁶. Due to the collective enhancement effect in the readout of spin-wave, the huge scale may become an advantage in metrology. The nonclassical correlations contained in the W state among huge entangled particles may endow quantum advantages over classical states, though it is still an open question how to sufficiently exploit the distinct features of such a large-scale W state.

Methods

Experimental details

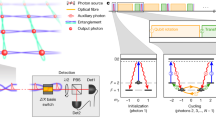
Figure 1a shows the energy levels of far-off-resonance DLCZ protocol, where the far-off-resonance regime means that the detuning is much larger than the Doppler broadening in the warm vapor cell. The large detuning in the generation and verification process can prevent the scattering signal photons from being immersed in the fluorescence noise, which endows a low unconditional noise level and a high cross-correlation²⁶. The pump and probe pulses are generated by the same distributed Bragg reflector laser(SLAVE laser), whose frequency is locked to an external cavity diode laser(MASTER laser). The MASTER laser provides a fixed frequency reference in the transition of 6S_1/2, F = 4 → 6S_3/2, F = 4 co 5 lines of cesium atoms. This frequency stabilizing system is not only important for W state’s creating and verifying, but also related to the performance of subsequent filtering systems. In this scheme, the pump and probe light are collinear with horizontal polarization, but the scattering correlated Stokes and anti-Stokes photons are in the vertical polarization because of the selection rules of the SRS process. To split the collinear Stokes and anti-Stokes photons, we have built two sets of high-performance Fabry-Pérot cavities to direct different photons into different counting modules, as Fig. 1b shows.

There are several elements that will influence the entanglement depth in the actual experiment, such as the beam waist, the detuning, and the energy of addressing light. For the far-off-resonance DLCZ protocol, we have chosen a “sweet point” (Δ = 4 GHz) for the detuning, which has been experimentally demonstrated to have the lowest unconditional noise^25,26. As for the beam waist, it is not appropriate to utilize a too large beam waist to provide enough addressing energy density. Note that there is no problem with using a larger beam waist while stronger addressing light is equipped, whose advantage is that there will be more atoms involved in the creation of an entanglement state. In our experiment, we choose a beam waist of 100 μm for providing a sufficient excitation rate. Our generating scheme of the W state is operated in a broadband feature benefiting from the condition of far detuning, so we can use 2 ns pulses to generate and verify the W state. To generate this high-speed light pulse with enough intensity in Fig. 1b, we have developed a system to satisfy the needs of tunable central frequency, broad bandwidth, and more importantly, generation time in a programable fashion. For observing the decoherence effects of the multipartite entanglement, we have chosen the appropriate pulse energy of 225 pJ. The whole time sequence for initializing, generating, and the verifying process can be depicted in Fig. 5. More information about the experimental parameters can be found in Supplementary Note 1.

Fig. 5: The time sequence of pulses used for generating and verifying entanglement.

The whole time sequence for initializing, generating, and verifying process. The initializing pump light used for preparing the initial state of atoms is in the transition from $\left|6{S}_{1/2},F=4\right\rangle$ to $\left|6{S}_{3/2},F=4\right\rangle$, and the 2 ns pulses for exciting and verifying the entanglement are applied when the pump light is off. The relative time information for the Stokes and anti-Stokes photons, created in the generating and verifying process, are recorded by the counting module of single photon detection. We have chosen six different delays to verify the evolutions of the W state from 30–1200 ns. For brevity, we have omitted the graphs of 120, 300, and 900 ns. The preparing time for the initial state in each trial is 700 ns, and the repeating period for each trial is 2.1 ns.

We can define the heralded probability of the retrieving anti-Stokes photon as p₁ in the verifying process, which can be expressed as ${p}_{1}=\frac{{N}_{S\cdot AS1}+{N}_{S\cdot AS2}}{{N}_{S}}$ with N_S⋅AS1(2) represents the coincidence of the Stokes photons and the anti-Stokes photons of two paths. To analyze the higher-order excitations, we using the standard HBT configuration to measure the three-fold coincidence, so the ${p}_{2}=\frac{2{N}_{S\cdot AS1\cdot AS2}}{{N}_{S}}$, where factor 2 is derived from the fact that there is a 50% chance for the two photons to go into different paths of the beam splitter. Based on the above definitions, we can construct a simple relationship between p₁ and p₂, i.e. ${p}_{2}=\frac{1}{2}{g}_{A{S}_{1}\cdot A{S}_{2}| S}^{(2)}{p}_{1}^{2}$, where the autocorrelation function ${g}_{A{S}_{1}\cdot A{S}_{2}| S}^{(2)}=({N}_{s}{N}_{S\cdot AS1\cdot AS2})/({N}_{S\cdot AS1}{N}_{S\cdot AS2})$ with the approximation N_S⋅AS1 ≈ N_S⋅AS2. Actually, it is reasonable for us to remove the loss of detection when we deals with the raw experimental data, because the genuinely verified entanglement depth can’t be varied with the detection loss and the loss can be accurately measured in our experiment. Therefore, the p₁, p₂ can be modified as ${p}_{1}^{\prime}=\frac{{N}_{S\cdot AS1}/{\eta }_{AS1}+{N}_{S\cdot AS2}/{\eta }_{AS2}}{2{N}_{S}}$,${p}_{2}^{\prime}=\frac{2{N}_{S\cdot AS1\cdot AS2}/{\eta }_{AS1}{\eta }_{AS2}}{{N}_{S}}$ (where the factor 2 in the denominator of ${p}_{1}^{\prime}$ comes from that ${p}_{1}^{\prime}$ is the sum of two anti-Stokes paths, and the detection losses η_AS1 = 1.95%, η_AS2 = 1.85% based on the experimental measurement), which indicates the photons statistics at the moment of having converted the W state into a mapping-out photon. The raw experimental data about p₁ = 0.0123 and p₂ = 2.49 × 10⁻⁵ with a memory time of 30 ns are shown in Fig. 2. After subtracting the detection inefficiencies, the genuine p₁ = 0.32 and p₂ = 0.017 with a memory time of 30 ns.

Witness for M-separability

In the certifying process, we apply an optical pulse to interrogate the state of the atomic ensemble, and analyze the correlated photons statistics. We assume that the atomic state can be described in a pure state, which can be decomposed into an M-separable form like equation $\left|\psi \right\rangle$ in the main text. Due to the imperfect experimental conditions and decoherence, the representation of the state in every independent subgroup may be a superposition of many possible states³⁷. Since we consider at most two excitations in the spontaneous Raman scattering process, the specific form of each state in the subgroup can be expressed in the following state

$$\left|{\phi }_{i}\right\rangle ={a}_{i}\left|{W}_{0}\right\rangle +{b}_{i}\left|{W}_{1}\right\rangle +{c}_{i}\left|{W}_{2}\right\rangle$$

(3)

where $\left|{W}_{1}\right\rangle$, $\left|{W}_{2}\right\rangle$ are the Dicke states in each subgroup; $\left|{W}_{0}\right\rangle$ is a vacuum state. Thus, the whole state of the ensemble is the product of all subgroups:

$$\left|{{\Psi }}\right\rangle ={\otimes }_{i = 1}^{M}\left( {a}_{i}\left|{W}_{0}\right\rangle +{b}_{i}\left|{W}_{1}\right\rangle +{c}_{i}\left|{W}_{2}\right\rangle \right)$$

(4)

The two probability p₁, p₂ can be calculated specifically,

$${p}_{1}=\frac{{\left|\mathop{\prod}\nolimits_{i = 1}^{M}{a}_{i}\right|}^{2}}{M}{\left|\mathop{\sum}\limits_{i}\left({b}_{i}/{a}_{i}\right)\right|}^{2}$$

(5)

$${p}_{2}=\frac{{\left|\mathop{\prod}\nolimits_{i = 1}^{M}{a}_{i}\right|}^{2}}{{M}^{2}(1-1/N)}{\left|\sqrt{2}\mathop{\sum}\limits_{i\,{<}\,j}\left[{b}_{i}{b}_{j}/({a}_{i}{a}_{j})\right]+\sqrt{1-1/D}\mathop{\sum}\limits_{i}\left({c}_{i}/{a}_{i}\right)\right|}^{2}$$

(6)

where $D=\frac{N}{M}$ is the entanglement depth. Actually, the entanglement depth should be defined as the largest scale of all the entangled subgroups, but we can take N/M as the representation of entanglement depth to avoid getting a very large subgroup size²¹.

In order to determine the entanglement depth in the experiment, we need to determine the lower bound for p₂ with a fixed M value. Obviously, we need the probability p₂ as low as possible in the actual experiment, which means that the fidelity of the target W₁ state is high. The bound can be calculated by

$${p}_{2}^{bound}({p}_{1},M)=min\left\{{p}_{2}| \psi :{p}_{1},M=const\right\}$$

(7)

Note that the constraint between the coefficients of superposition in eq. (3) is, ${\left|{a}_{i}\right|}^{2}+{\left|{b}_{i}\right|}^{2}+{\left|{c}_{i}\right|}^{2}\le 1$, and we can take the approximation ∣a_i∣² + ∣b_i∣² + ∣c_i∣² = 1 owing to the neglectable higher-order excitations. Utilizing the Lagrange multiplier method deduced in the supplementary notes of²¹, the conclusion is that the symmetric solution gives the global minimal value of p₂ for M≥5. This symmetric solution requires that ${a}_{i}=a,{b}_{i}=b,c=-\sqrt{1-{a}^{2}-{b}^{2}}$. In this condition, the optimal values for p₁, p₂ are

$${p}_{1}^{sym}=M{a}^{2M-2}{b}^{2}$$

(8)

$${p}_{2}^{sym}={a}^{2M}{\left[\frac{1}{\sqrt{2}}(M-1)\frac{{b}^{2}}{{a}^{2}}+\frac{c}{a}\right]}^{2}$$

(9)

The final form of function ${p}_{2}^{bound}({p}_{1},M)$ is,

$${p}_{2}^{bound}({p}_{1},M)={a}^{2M}{\left[\frac{1}{\sqrt{2}}\frac{{p}_{1}(M-1)}{M}{a}^{-2M}-\frac{1}{a}\sqrt{1-{a}^{2}-\frac{{p}_{1}}{M}{a}^{2-2M}}\right]}^{2}$$

(10)

For fixed p₁ and M, we need to calculate minimal value of p₂ with a ∈ (0, 1). The theoretical bound of eq. (10) can be obtained by taking all values of p₁ ∈ (0, 1), which is shown in Fig. 2a and Fig. 3b with different M values.

Number of atoms involved in the creation of multipartite entanglement

Theoretically, the transmission rate of probe light passing through the atomic ensemble has the following form^38,39

$$T(\omega )=exp\left\{-2\pi nkL{d}^{2}/(h{\varepsilon }_{0})\mathop{\sum }\limits_{i=1}^{3}{S}_{i}{l}_{i}(\omega )\right\}$$

(11)

where n is the density of atoms, k is the wave vector of the probe light, L is the length of our vapor cell, d is the reduced dipole matrix element, S_i is the strength of relative coupling from the hyperfine level F = 3 of the ground state to $F^{\prime} =2,3,4$ in the excited state⁴⁰, l_i(ω) is the normalization lineshape. For more precisely fitting, the normalization lineshape l_i(ω) should be considered as Vigot lineshape³⁹. More details about the theoretical absorption model and experimental fitting are in Supplementary Note 2. According to the fitting coefficients, the number density of atoms in the ¹³³Cs cell is nearly 1.21 × 10¹⁸ m⁻³.

To determine how many atoms participating in the interaction, we need to know the volume of the interaction area illuminated by light in the creating and certifying process. Considering the coherence length of the atomic ensemble, the actual volume of the atoms involved in the W state may be delocalized in a subensemble. There is a simple model to analyze the coherence volume of the ensemble according to the collective enhancement effect in the superposition of the transformed anti-Stokes photon. While the probe light is applied for transforming the W state into an anti-Stokes photon, many atoms will collectively participate in this process. This collective enhancement of the wave function of the anti-Stokes photon is derived from the coherent superposition of the whole ensemble, which can be expressed as

$$\left|{{{\Psi }}}_{as}\right\rangle =\mathop{\sum }\limits_{j=1}^{N}\frac{1}{\sqrt{N}}{e}^{i({k}_{w}+{k}_{p}-{k}_{as})\cdot {r}_{j}}\left|{\phi }_{0}\right\rangle$$

(12)

where k_w is the wave vector of the W state correlated to the pumping process with the form of k_w = k_p − k_s, k_p is the wave vector of the pump or probe light, k_s and k_as are the wave vectors of the Stokes and anti-Stokes photons respectively, N is the number of involving atoms, $\left|{\phi }_{0}\right\rangle$ is the spherical wave function of the single photon. Therefore, the coherence of the anti-Stokes photon is related to the mismatch wave vector Δk = 2k_p − k_s − k_as. In the ideal case, the excitation process satisfies the matching condition of wave vectors, i.e. Δk = 0, then the $\left|{{{\Psi }}}_{as}\right\rangle$ is in a state of coherent superposition, which will amplify the excitation probability of the anti-Stokes photon being proportional to the atomic number N. However, the collections of the Stokes and anti-Stokes emission are defined with a range of k-vectors at slightly different angles, so there may be small mismatching of the wave vectors in the actual experiment, which means that the uncertainty of the wave vectors implies a limit on the scale of the atomic ensemble that can be considered in the coherent superposition. The maximum mismatching angle is determined by the maximum collection angle of the single-mode fiber. Even though the single-mode fiber can define a well spatial mode with a very small divergence angle, the actual mismatching situation still sets the limit of the spatial scale of the ensemble to compose the W state.

Supposing the maximum collection angle defined by the single-mode fiber is θ, we can build a simple analyzing model to determine the spatial bound of the subensemble which contributes to the coherent superposition. Figure 6 shows the maximum mismatching of Δk_max, decomposed into two components, i.e. the longitudinal component ${{\Delta }}{k}_{max}^{\parallel }$ and the transverse component ${{\Delta }}{k}_{max}^{\perp }$, which can determine the length l and radius r of the coherent subensemble. For satisfying the coherent superposition of eq. (12), the phase accumulation by the mismatching of wave vectors cannot be much larger than 2π, so the components ${{\Delta }}{k}_{max}^{\parallel }$ and ${{\Delta }}{k}_{max}^{\perp }$ should meet the constraints: ${{\Delta }}{k}_{max}^{\parallel }\cdot l\le 2\pi$, ${{\Delta }}{k}_{max}^{\perp }\cdot 2r\le 2\pi$. Due to that the collection angle θ is extremely small, we can approximately take ${{\Delta }}{k}_{max}^{\parallel }={k}_{p}\cdot {\theta }^{2}$ and ${{\Delta }}{k}_{max}^{\perp }=2{k}_{p}\cdot \theta$, then we can evaluate the coherent bound of the subensemble l ≈ λ/θ², r ≈ λ/4θ, and the coherent volume can be calculated as V_coh = πr² ⋅ l = λ³/(16θ⁴). The maximum mismatching angle is determined by the maximum collection angle of the single-mode fiber. For our experimental parameters, the maximum collection angle is θ_SM = 2.7 × 10⁻³ rad. However, considering the spontaneous Raman scattering process in the generation process, the forward signal mode, correlated with the W state, is distributed inside a small cone, whose spatial structure can be read as⁴¹

$${f}_{{{\Omega }}}(\theta )={\eta }_{0}exp(-\frac{1}{4}{\eta }_{0}{k}_{0}^{2}{R}_{0}^{2}si{n}^{2}\theta )sinc({k}_{0}Lsi{n}^{2}\frac{\theta }{2})$$

(13)

where ${\eta }_{0}={r}_{0}^{2}/({r}_{0}^{2}+{R}_{0}^{2})$ is the structure factor of the actual atomic ensemble, r₀, and R₀ characterize the radius of the pump beam and the radius of the atomic ensemble, L is the length of the ensemble, k₀ is the wave vector of the signal photon. Therefore, the forward signal photons characterized by the experimental parameters will be distributed below the angle of ${\theta }_{FS}=\frac{1}{2}min[1/({k}_{0}{R}_{0}\sqrt{{\eta }_{0}}),1/\sqrt{{k}_{0}L}]$ and the actual bound of the angle of phase mismatching should be determined by θ_bound = min[θ_FS, θ_SM] = 6.7 × 10⁻⁴ rad. According to the maximum angle θ_bound of phase mismatching, the maximum size of a coherent atomic ensemble can be calculated as l_bound = 3.5 m, r_bound = 429.2 µm, while our vapor cell used in the actual experiment has the length of 7.5 cm and the radius of 2.5 cm. So, the real atoms involved in the W state may be delocalized in a subensemble with the bound of transverse radius being 429.2 µm.

Fig. 6: The phase mismatching in the read out of W state.

a The case of phase matching with Δk = 0. b The case of the maximum phase mismatching with Δk = 2k_p − k_s − k_as.

In order to make the evaluation of atomic number more reasonable, we have also taken the variations of the Gaussian beam radius into consideration. Along the propagating direction of light, the different beam radiuses of the pumping Gaussian beam at different positions and the transverse radius determined by the uncertainty of wave vector need to be considered while calculating the volume of the coherent subensemble. The condition of maximum phase mismatching delivers the transverse bound of a coherent ensemble, which can not excess r_bound = 429.2 µm. In other words, the transverse radius of the interaction area should be limited by r = λ/4θ when the radius of the Gaussian beam excesses r_bound. Therefore, we can define the effective coherent volume as

$${V}_{eff}=\pi /{{{\Gamma }}}_{0}\int\nolimits_{-L/2}^{L/2}[\int\nolimits_{0}^{\frac{\lambda }{4W(z)}}ln10{f}_{{{\Omega }}}(\theta ){W}^{2}(z)+\int\nolimits_{\frac{\lambda }{4W(z)}}^{{\theta }_{bound}}{f}_{{{\Omega }}}(\theta ){r}^{2}(\theta )]d\theta dz$$

(14)

where the beam radius $W(z)={W}_{w}{(1+{z}^{2}/{z}_{w}^{2})}^{1/2}$ (W_w is the beam waist and z_w is Rayleigh length of a laser beam), ${{{\Gamma }}}_{0}=\int\nolimits_{0}^{{\theta }_{bound}}{f}_{{{\Omega }}}(\theta )d\theta$ is the normalization factor of the spatial weight function f_Ω(θ). Here, we define the effective area of the Gaussian beam by the amplitude decreasing to 1/10 of maximum magnitude. Actually, the witness applied to certify the W state doesn’t require equal amplitude for the superposition of $\left|{W}_{1}\right\rangle$²¹, therefore more atoms can be taken into calculations owing to the extension of the Gaussian beam’s intensity. If the Gaussian beam radius is much smaller than the coherent bound r_bound in the whole atomic ensemble, the effective coherent volume defined as eq. (14) can be reduced into a simple form ${V}_{eff}=\pi ln10\int\nolimits_{-\frac{L}{2}}^{\frac{L}{2}}{W}_{z}^{2}dz$.

In our experiment, the Gaussian beam has the beam waist of W_w = 100 × 10⁻⁶ m, the Rayleigh length of z_w = 3.69 × 10⁻² m, and the length of the cesium cell is L = 75.3 × 10⁻³ m, so the maximum beam radium located in the end of the cesium cell is W(L/2) = 142.8 µm, which is much smaller than the limited transverse radium by the coherence. Therefore, the volume determined by the pumping Gaussian beam can be regarded as a well-defined coherent ensemble inside the whole atomic ensemble. As the main text said, the volume defined by Gaussian beam reads as ${V}_{Gaus}=\pi ln10\int\nolimits_{-\frac{L}{2}}^{\frac{L}{2}}{W}_{w}^{2}(1+{z}^{2}/{z}_{w}^{2})dz$, and we can define a localized factor ζ to characterize the locality of the entangled volume, which can be expressed as ζ = V_Gaus/V_coh = 1.5 × 10⁻¹⁵ < <1. Finally, the total number of atoms involved in the creation of entanglement is N = nV = 8.85 × 10⁹.