Introduction

High harmonic generation (HHG), initially observed in rare gas atoms, has recently attracted substantial interest in the attosecond and strong-field processes in solids1,2,3,4,5. HHG provides a unique tool to probe optical susceptibility, band structures, and electron dynamics of solids and liquids6,7,8,9,10,11,12. In terms of applications, solid-state HHG provides an effective coherent light source for extreme ultraviolet radiation, making it of significant importance to understand and control the nonlinear optical phenomena to engineer the emitted harmonics characteristics13,14,15,16,17,18,19. The underlying mechanism responsible for HHG in solids mostly involves two emission pathways: i) light emission from the accelerated electrons within a band under an external driving field, also known as intraband process and ii) light emission from electron-hole recombination, that is, interband process14,15,16,17. These two pathways depend on both material and external driving-field properties, e.g. the band structure, carrier density, laser polarization, and ellipticity, which have been used for effectively tuning the spectral and temporal properties of the HHG emission, as well as probing electron dynamics in real time8,18,19,20,21,22,23,24.

Periodic solids host collective lattice vibrations, or phonons, that are widely present either thermally, incoherently or coherently, which can modify the electronic, optical, and magnetic properties of materials25,26,27,28,29,30,31,32,33,34,35,36,37. Since solid HHG is sensitive to dynamical variations in the electronic density and nuclei potential, one could manipulate, by exciting phonons, the emitted harmonics characteristics15. Such use of an internal degree of freedom in the lattice has so far not been systematically explored as a control method for HHG from solids. Recently, Ginsberg et al. illustrated the impact of the phonons on the second and third harmonic generation, and showed that the emitted yields are sensitive to lattice vibrations in hexagonal-Boron-Nitride (hBN)25. It was also shown that lower-order harmonics can be sensitive to coherent phonon dynamics in vanadium dioxide26, and that the carrier envelope-phase of the driving field can play an additional role in phonon HHG spectroscopy27. In this regard, coherently excited phonons provide a promising strategy to engineer or probe ultrafast nonlinear dynamics in solids. However, the scope of how to utilize collective lattice dynamics to control HHG in different materials is largely unrarely explored; more importantly, the underlying microscopic mechanism for such phonon-assisted HHG has not been investigated in detail.

Here, we show how coherent optical phonons affect HHG from several prototype layered materials (graphite, 2H-MoS2, and hBN) and covalently-bonded solids (diamond) using time-dependent density-functional theory (TDDFT) coupled to classical nuclei motion38,39,40,41,42,43,44,45. The phonon-assisted HHG spectra from solids strongly depend on both the specific solid and the characteristics of the excited phonon modes. In bulk hBN, for example, the simulated high-harmonic yields can be significantly enhanced by a factor of ~20 in the presence of transverse optical (TO) phonon with E1u mode at 7.3 μm. We reveal that the lattice vibrations effectively help promote the excited carrier dynamics and boost the photoinduced doping, which is the source of the harmonic yield enhancement. Our work implies that phonon pumping provides a new degree of freedom to optimize HHG from condensed matter.

Results and discussion

Phonon-assisted HHG in bulk hBN

In the family of layered materials, both the strong in-plane bonding and the weak van der Waals interactions between layers provide a variety of degrees of freedom in lattice vibrations and electronic structures. In this regard, we first focus on the effect of the optical phonons on HHG in several layered solids (e.g., hBN, graphite, and 2H-MoS2). The phonons are prepared by setting an initial displacement on the ions along the eigenmode direction (see Methods). We then propagate the electron-phonon coupled dynamics within the framework of TDDFT for the electrons coupled to the Ehrenfest dynamics for the classical ions38. We validate this approach, by comparing the results to the case where the collective lattice motion was initiated following interactions with a phonon-mode-resonant THz laser pulse.

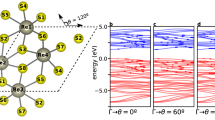
To demonstrate the role of phonons in the HHG emission from solids, we first consider an in-plane TO phonon with E1u mode at Γ point in hBN. Such phonon mode can induce broken inversion symmetry when strongly excited by a laser pulse with a wavelength of 7.3 μm (~170 meV)25. The atomic displacements of the mode in the adjacent hBN layers are in opposite directions within the hBN plane, leading to a net change in the polarizations, as shown in the inset of Fig. 1a. Phonon modes in hBN are prepared by setting an initial velocity on the ions along the eigenmode displacement direction by 1% of the lattice parameter and we then propagate the Ehrenfest dynamics together with the TDDFT. To check the method, we also applied pump laser pulses with the same frequencies and polarizations of phonon modes of hBN and tracked the atomic displacements. Our calculations confirm the two methods are equivalent in the simulations of high-harmonic generation.

Fig. 1: HHG spectra from layered materials assisted with phonons.
figure 1

a HHG spectrum for hBN with the excitation of the TO (E1u mode at Γ point, red curve) and with the frozen ions (blue curve). We employ a laser pulse with a wavelength of λ = 800 nm (i.e., ħω = 1.55 eV) and I0 = 1 × 1012 W cm–2. The adjacent hBN layers stack laterally with the AA’ configuration of a hexagonal structure. b HHG spectrum for graphite with the excitation of the TO (E1u mode at Γ point, red curve) and with the frozen ions (blue curve). The laser wavelength is λ = 1.6 μm (ħω = 0.78 eV) and the intensity is I0 = 1 × 1011 W cm−2. The adjacent carbon layers stack laterally with the AB configuration of a hexagonal structure. c HHG spectrum for 2H-MoS2 with the excitation of the TO (\({E}_{2g}^{1}\) mode at Γ point, red curve) and with the frozen ions (blue curve). The laser wavelength is λ = 4.133 μm (ħω = 0.3 eV) and the intensity is I0 = 1 × 1011 W cm−2. The insets show the atomic displacements of the corresponding modes. The black arrows mark the corresponding cutoff energies of the phonon-mediated spectra. The harmonic intensity is probed along the direction parallel with the laser polarization of the corresponding applied laser pulse.

Full size image

Figure 1a shows that excited phonons can significantly modify the HHG spectrum of hBN. For the phonon-free system, clean harmonic peaks are observed up to the 29th order; that is, for the pump laser with a wavelength of 800 nm (~1.55 eV), the estimated cutoff energy for the HHG plateau is 45 eV (\(\approx\)29×1.55 eV). In the presence of a coherent TO mode (E1u at the Γ point, Supplementary Fig. S1), the intensity of the harmonics up to the 7th order is enhanced compared to the phonon-free case, while harmonic orders beyond 7 can no longer be distinguished. As expected, even-order harmonics (the 2nd, 4th and 6th orders) appear due to the phonon-induced symmetry breaking in the adjacent layers13,45. We only focus on the phonon mode at Γ point because of energy and momentum conservation. Furthermore, a 2 × 2 × 1 hBN supercell is employed to confirm the spectrum with the supercell, indicating the unit cell is enough to illustrate the phonon-mediated harmonics, as shown in Supplementary Fig. S2.

As a striking point, the spectra obtained in the presence of excited phonons seem to be noisy and do not display a clear odd-harmonic structure, for example, see Fig. 1a–c. This results from the phonon sidebands, which are generated due to the presence of two harmonic content: i) the electron frequencies, which are the odd-integer multiple of the laser field, and ii) the frequency of the phonon. In hBN, the yields of some even-order harmonics are comparable to that of odd-order harmonics. This is mainly attributed to the breaking of inversion symmetry caused by collective lattice vibrations (phonons), which is supported by recent experiments25.

As an example of this, a peak at an energy of 0.17 eV appears in Fig. 1a, which corresponds to the energy of the vibrations of the E1u mode in hBN (where electrons adiabatically follow the lattice). For a more general perspective, we also explore the HHG spectrum with a driven longitudinal optical mode with the same frequency (see Supplementary Fig. S3). The corresponding HHG spectra show a similar trend to that for the excited TO case, where there is however a comparatively smaller increase in the intensity of the even-order harmonics. This also demonstrates that the spectra contain mode-selective information that might be useful for identifying the exact optically active phonon.

We next perform a more detailed analysis of the harmonic yield changes due to excited optical phonons in hBN. For simplicity, we consider the total yield that is computed by integrating the HHG yield between 4 and 12 eV (roughly from the 3rd to the 8th harmonics). As a result, a 17-fold enhancement is observed for the TO (E1u) mode while a 16-fold increase is obtained for the LO (E1u) mode. In short, by pre-exciting optical phonons, the total harmonic yields can be enhanced by more than an order of magnitude. It should be noted that a laser pulse with the 7.3 µm can excite the IR-active TO (E1u) mode directly25. See Supplementary Fig. S4 for the details on the effect of the phonon amplitude and Supplementary Fig. S5 for the case with thermally excited phonons at 300 K.

Phonon-assisted HHG in graphite and 2H-MoS2

To generalize these findings, we further study other layered materials with distinct electronic structures, e.g., graphite with zero bandgap and semiconducting 2H-MoS2. Furthermore, we extend our simulations to a non-layered system, diamond (Supplementary Fig. S6). From these materials, we find a clear physical picture of the harmonic emission mediated by optical phonons as will be discussed below.

For graphite, the infrared-active TO (E1u) mode with a frequency of ~1600 cm−1 (corresponding to 0.2 eV)46 hosts atomic displacements with antiphase motion in the two adjacent graphene planes. Figure 1b presents the HHG spectra with and without an excited TO mode (E1u at the Γ point). For a pump laser pulse with a wavelength of 1.6 μm, the phonon-free spectrum exhibits clear peaks up to the 5th order, which is equivalent to a cutoff energy of 3.87 eV. With the E1u phonon excited, the yield for the harmonics up to the 7th order is enhanced by a factor of 3.7. Similar to hBN, no clear harmonic peaks are visible due to the importance of excited sidebands.

For 2H-MoS2, we focus on the Raman-active TO (\({E}_{2g}^{1}\)) mode at the Γ point (with an energy of 0.3 eV) with in-plane atomic displacements. In Fig. 1c, for the phonon-free case, harmonic peaks up to the 11th order (corresponding to the cutoff energy of ~3.3 eV) are clearly observed. With a pre-excited \({E}_{2g}^{1}\) mode, the HHG cutoff energy extends to 6.9 eV (the 23rd order). Moreover, the harmonic efficiency below the cutoff energy increases, and the associated harmonic yield doubles compared to the phonon-free case (computed by integrating the spectrum between 1 and 7 eV). To illustrate the role of different modes, we also study the effects of a pre-excited out-of-plane A1g mode on the HHG spectra (Supplementary Fig. S7). We find that the phonon-induced modification in the plateau from the A1g mode is smaller compared to the \({E}_{2g}^{1}\) mode. This comparison indicates that different modes affect the strong-field induced electron dynamics in different ways, and that this effect can be probed by HHG.

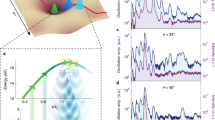
To explore the temporal characteristics of the electron dynamics, we perform a time-frequency analysis below; such analysis can illustrate how the HHG response builds up in time and allow us to estimate the emission and return times of the electron dynamics, the kinetic energies, and their role in the harmonic spectrum47,48. The time-frequency analysis in HHG is a powerful tool that combines temporal and spectral analysis to provide a comprehensive understanding of the ultrafast processes involved in high-harmonic generation, involving a windowed Fourier transform of the induced current.

Figure 2 exhibits the time-frequency analysis of harmonic emission for the bulk materials with corresponding excited phonons. For hBN, we can make out short and long HHG electron dynamics, as have been well established21,22. However, we observe that the specific characteristics become slightly attenuated along the laser pulse, corresponding to the instantaneous changes in the lattice structure induced by the collective lattice motion. In other words, the HHG emission is asymmetric between adjacent laser cycles, which also contributes to the noisier spectra observed with no apparent odd-harmonic peaks because temporal translation symmetry is broken27 and phononic sidebands are generated28. Largely similar results are observed for graphite and 2H-MoS2 (Fig. 2b, c), though here the phonon-induced modification to the electronic dynamics is even more significant, and we can make out particular laser cycles that dominantly contribute to the response in certain spectral regions. For instance, in graphite the HHG emission from ~3 to 6 eV is dominantly contributed by one laser cycle after the envelope peak power [around 30 fs, see Fig. 2b]. The excited lattice vibrations increase the portion of electrons excited to the conduction bands by strong pulses, therefore, introducing the phonon-enhanced carrier concentrations. As we will show below, one main effect of the pre-excited phonon dynamics on the electronic response is to allow enhanced excitations to the conduction bands, therefore, introducing phonon-enhanced carrier concentrations.

Fig. 2: Laser-induced total currents and time-frequency analysis of harmonic emissions.
figure 2

a Time-frequency analysis of harmonic emissions for hBN with the TO (E1u) mode. At different times (x-axis), the intensity illustrates the emitted harmonics with corresponding energy (y-axis). b The same quantity as (a) for graphite with TO (E1u) mode. c The same quantity as (a) for MoS2 with the \({E}_{2g}^{1}\) mode. The vector potentials of the applied laser pulses are shown in a-c (white curves), respectively.

Full size image

Intensity dependence of phonon-assisted HHG spectra

Next, we focus on how the enhancement of the HHG spectra due to optical phonons depends on the laser pulse characteristics14,15,16. We use hBN as an example and compute its harmonic yields in the presence and absence of optical phonons under three pump intensities (I0) (see Fig. 3). For the phonon-free case, we observe clean harmonic peaks with significantly larger efficiencies for a larger intensity of I0 = 5 × 1012 W/cm2. As for the TO (E1u) phonon case, the harmonic efficiencies of the harmonics increase significantly due to the stronger laser intensity (see below for the comparison of the harmonic yields). In addition, the cutoff energy of the harmonic plateau increases from the 7th to the 11th order (equivalent to an energy of 17.1 eV) due to the stronger laser intensity. In this regard, the phonon seems to lead to a reduction in the energy cutoff.

Fig. 3: Strength dependence of the phonon-assisted harmonic spectra.
figure 3

a Laser strength dependence of the harmonic yields for bulk hBN with the frozen ions. For the probe pulse, we employ an in-plane driving electric field with a wavelength of λ = 800 nm with different intensities (I0) and the polarization is parallel to the vibrational mode of TO (E1u) mode. b The same quantity as (a) for the conditions with the excited TO (E1u) mode.

Full size image

From the HHG spectra of 2H-MoS2 [Fig. 1c], we find a small change in the harmonic yield for harmonics with energies below the bandgap (~0.9 eV in our simulations). In contrast, we observe a significant change in the harmonic intensity for the 9th-21st orders with energies above the bandgap. Such results indicate that the interband mechanism for HHG is more sensitive to the collective lattice movements. This is further supported by the sidebands in the HHG spectrum, demonstrating that the interband transition plays a dominant role when the phonons are evoked.

We note that the HHG spectra obtained in the presence of the TO excited optical phonons are more structured and do not display a clear odd-only harmonic structure. This in fact results mostly from the presence of phonon-induced sidebands, which are generated due to the presence of electron and phonon frequencies [See SI for more details]. The sideband effect can also well explain the dip at the even harmonic position in our simulations. The energy width of two split peaks of even harmonics is nearly twice of the energy of the TO mode, indicating that the first sidebands as more intense than the even-harmonic response. While phonons may enhance the overall signal, the smoothing effect on higher harmonic peaks can have important implications for the spectral characteristics, efficiency, and interpretation of EUV generation processes. Understanding and mitigating these effects are crucial for advancing the field and optimizing the performance of EUV sources for various applications.

Phonon-enhanced photodoping effect

To explain the phonon-mediated harmonic yields, we inspect the photon-induced carrier doping in the systems, i.e., the time evolution of the number of excited electrons. Figure 4a shows the number of excited electrons in hBN as a function of time for three different laser pulse intensities. Compared to the phonon-free case, more charge carriers are excited from valence bands to conduction bands [Fig. 4b and Supplementary Fig. S8]. For instance, for the intensity of I0 = 1 × 1012 W/cm2, the number of the excited electrons due to the TO (E1u) mode is 8.5 times larger than that for the phonon-free case. The enhancement of photodoping implies a strong nonlinear interaction between the coherent phonons and the electronic states. The amplification effect suggests that coherent phonons are not just a perturbative factor but play a significant role in modulating the carrier density. The mechanisms could be interpreted by enhanced carrier injection by providing additional energy and increase the probability of tunnelling, thereby contributing to the carrier density.

Fig. 4: Photon-induced doping effects in enhanced harmonic efficiency.
figure 4

a Numbers of excited electrons as a function of time in hBN with the excited TO (E1u) mode under different laser intensities. b Numbers of excited electrons for the phonon-free case at the end of the laser pulses and the excited phonon case in bulk hBN for different laser intensities. The excited electrons indicate the number of photoexcited electrons after the laser pulse (t = 50 fs) as shown in a. c The dependence of harmonic enhancement (\(\frac{{Y}_{{Phonon}}}{{Y}_{{Frozen}-{ions}}}\)) on photoinduced carrier enhancement (\(\frac{{N}_{{Phonon}}}{{N}_{{Frozen}-{ions}}}\)). The harmonic yields are integrated over the harmonic plateaus for the corresponding materials. Different points are from various laser powers, and the initial phonon displacements are kept the same. Blue and red dots indicate the dependence of harmonic yield enhancement on the carrier enhancement for graphite and MoS2, respectively. The gray line is a guide for the eyes.

Full size image

To find a quantitative relationship between the photodoping carrier density and the phonon-enhanced harmonic yield, we first use hBN as an example and compute its harmonic yield evaluated using the plateau region between 4 and 12 eV. Figure 4c shows a nearly linear relation between the harmonic enhancement and the photoexcited carrier enhancement for hBN. Here, the harmonic yield and the photoexcited carrier enhancement are defined as \(\frac{{Y}_{{Phonon}}}{{Y}_{{Frozen}-{ions}}}\) and \(\frac{{N}_{{Phonon}}}{{N}_{{Frozen}-{ions}}}\), respectively, where \({Y}_{{Phonon}}\)(\({Y}_{{Frozen}-{ions}}\)) and \({N}_{{Phonon}}\)(\({N}_{{Frozen}-{ions}}\)) are the harmonic yield and the number of excited carriers with (without) the excited phonons, respectively. Our results illustrate that phonons can modulate light-induced carrier excitations, which in turn significantly increase the harmonic yields. We also obtain similar trends for the excitation dynamics in graphite and 2H-MoS2 (Supplementary Fig. S9). With the excited phonon, the photoinduced carrier concentration increases by 2.1 (2.5) times for graphite (MoS2), compared to the phonon-free case. Putting all the above materials together, we obtain a universal curve between the phonon-enhanced harmonic efficiency and the laser-enhanced carrier density [Fig. 4c]. In addition, we excited both TO (7300 nm) and LO (6200 nm) modes to confirm the scaling. Our analysis on the harmonic yield and carrier enhancement follows the same trend with the single mode excited cases [Supplementary Fig. S10]. Our results indicate that the photodoping carrier density in solids is strongly correlated to the phonon excitation, and is thus one of the crucial ingredients in phonon-assisted HHG.

The mechanism can be interpreted as follows: photocarriers are produced by generating excited electron-hole pairs when a laser field is strong enough to introduce interband Zener tunnelling with significant probability. The enhancement of photodoping implies a strong nonlinear interaction between the coherent phonons and the electronic state. The coherent phonons can interact with electronic states, influencing carrier dynamics. The amplification effect suggests that coherent phonons are not just a perturbative factor but play a significant role in modulating the carrier density. This is indeed distinct from the linear perturbation, which typically would result in much smaller changes. The mechanisms could be explained by strong nonlinear electron-phonon coupling and dynamic band modulation [Supplementary Fig. S11]. However, the exact contribution of interbond Zener tunneling is hard to be extracted because all interactions are entangled and attribute to the total photoinduced current and harmonics.

As observed, the photoinduced carrier concentration is effectively enhanced from collective lattice vibrations and corresponding phonon-modulated electronic structures. On one hand, the phonon-induced carrier density would boost the harmonic yields from the intraband mechanism, naturally attributed to Bloch oscillation. On the other hand, the enhanced carriers provide more channels and increase the possibility of electron-hole recombination. Therefore, the contribution from interband transitions is improved as well. Previously, the phonon-assisted HHG process was reported to be sensitive to the pump-probe delay and carrier-envelope phase of driving fields27. The enhancement or suppression in the harmonic efficiency is associated with instantaneous changes in the lattice structure (bond compression or stretching) and modulation of the electronic structures, which should be accompanied by photodoping densities at various pump-probe delays.

Furthermore, we compare our results in context with some relevant experimental studies. Wang et al.23 showed that the suppression of the interband HHG yield in ZnO is attributed to the pre-photodoping effect, which depletes the carriers in the valence band and leads to fewer electrons contributing to emitting harmonics. In another study, Nishidome et al.24 demonstrated that the harmonic yields of the single-walled carbon nanotube can be tuned by injecting carriers into the nanotube via electrolyte gating. We find that the phonon-assisted photodoping carriers are coherent with the laser pulses, and more excited electrons are involved to emit harmonics with phonons. Our work, together with the above studies23, points out that more excited carriers lead to stronger harmonic yields, which is attributed to the phonon-assisted tunneling to the conduction bands. In this work, we do not investigate the effects on HHG yields due to the pump-probe delay or carrier-envelope-phase, which could play an additional role in controlling phonon-assisted HHG yields (depending on the laser parameter regime)27 and would be the future work. Our results emphasize the importance of ionic movements in optical nonlinearity, which can be extended to a situation where multi-phonons are involved in emitting high-order harmonics.

In summary, we have investigated the effects of coherent optical phonons on HHG from typical solids using TDDFT coupled to classical ionic dynamics. The excitation of optical phonons enhances high-order harmonic yields, but less clear high-order harmonic peaks are observed due to the generation of phononic sidebands. The underlying mechanism for the enhancement of the harmonic yield is that the phonons can effectively assist in promoting photoexcited carriers, which results in increasing harmonic emissions. Overall, our results provide a new platform to study strong-field physics in solids, and reveal the importance of lattice degrees of freedom for controlling harmonic emission.

Methods

TDDFT calculations

The time evolution of the wave functions and the evaluation of the time-dependent electronic current were computed by propagating the Kohn–Sham equations in real space and real time, as implemented in the Octopus code40,41,42 with the adiabatic LDA functional44. All calculations were performed using fully relativistic Hartwigsen, Goedecker, and Hutter (HGH) pseudopotentials45. In our simulations, the laser pulses are treated using the velocity gauge and the induced vector fields are imposed to be time-dependent but homogeneous in space, and we use a sin-square pulse envelope.

The full harmonic spectrum is computed directly from the total electronic current density j(r, t) as shown in Fig. 1.The full harmonic spectrum is computed directly from the total electronic current density j(r, t) as shown in Fig. 1.

$${HHG}\left({\rm{\omega }}\right)={\left|{FT}\left(\frac{\partial }{\partial t}\int {d}^{3}{\boldsymbol{r}}{\boldsymbol{j}}\left({\boldsymbol{r}},t\right)\right)\right|}^{2}$$
(1)

where FT denotes the Fourier transform. We note that both electronic and ionic currents contribute to the HHG spectra in experimental measurements. In our simulations, the ionic current from lattice vibrations contributes negligibly, compared with the electronic current.

The time-frequency analysis describes how the HHG builds up in time and is obtained by performing a windowed Fourier transform of current,

$$G({\rm{\omega }},{t}_{0})={\left|\int {dt}{\partial }_{t}\,{\boldsymbol{j}}\left(t\right){e}^{\frac{{\left(t-{t}_{0}\right)}^{2}}{{\sigma }^{2}}}{e}^{-i{\rm{\omega }}t}\right|}^{2}$$
(2)

The number of excited electrons (Nex) is calculated by projecting the time-evolved wavefunctions \((|{\psi }_{n,{\boldsymbol{k}}}(t)\rangle )\) on the basis of the ground-state wavefunctions \((\,|{\psi }_{n^{\prime} ,\,{\boldsymbol{k}}}^{{GS}}\rangle )\).

$${N}_{{ex}}\left(t\right)={N}_{e}-\frac{1}{{N}_{k}}\mathop{\sum }\limits_{n,\,{n}^{{\prime} }}^{{occ}}\mathop{\sum }\limits_{k}^{{BZ}}{\left|\left\langle {\psi }_{n,{\boldsymbol{k}}}\left(t\right),|,{\psi }_{{n}^{{\prime} },{\boldsymbol{k}}}^{{GS}}\right\rangle \right|}^{2}$$
(3)

where Nex is the total number of electrons and Nk is number of k-points used to sample the Brillouin zone (BZ). The sum over band indices n and n’ go over all occupied states. It should be noted that ground-state wavefunctions are dependent on the time-propagated atomic coordinates. In this regard, self-consistent calculations are performed using the time-dependent atomic structures every 0.3 fs to obtain the ground-state wavefunctions.

Simulations of HHG from bulk hBN

The real-space cell was sampled with a grid spacing of 0.4 Bohr and the Brillouin zone was sampled with a 42 × 42 × 21 k-point grid to sample the BZ, which yielded highly converged results for hBN. The boron nitride bond length is taken here as the experimental value of 1.445 Å. Within the LDA functional, the bandgaps of hBN are 4.6 eV. We consider a laser pulse of 25-fs duration at full-width half-maximum (FWHM) with a sin-square envelope, and the carrier wavelength λ is 800 nm, corresponding to 1.55 eV, polarized along xxx.

Simulations of HHG from graphite and bulk MoS2

For graphite, the experimental lattice constant is used (1.42 Å) in our simulations with a 42 × 42 × 21 k-point grid to sample the BZ. The real-space cell was sampled with a grid spacing of 0.4 Bohr. The laser pulse of 25-fs duration at FWHM is considered with a sin-square envelope, and the carrier wavelength λ is 1600 nm, corresponding to 0.78 eV. We used a peak intensity of I0 = 1011 Wcm−2.

For bulk MoS2, we used a real-space spacing of 0.35 Bohr and a mesh of 24 × 24 × 12 to sample the BZ of MoS2. The lattice constant of MoS2 is 3.16 Å. A carrier wavelength of λ = 4133 nm was used, corresponding to a carrier photon energy of 0.3 eV. The peak intensity in vacuum is I0 = 1011 Wcm−2. In our simulations, a longer laser pulse (FWHM = 50 fs) is employed, in order to fully cover the lattice vibrations of\(\,{E}_{2g}^{1}\) phonon mode at Γ point. The phonon modes of MoS2 is prepared by starting by the time-evolution from a distorted atomic configuration along the phonon modes of 4% of the lattice constant because smaller displacements result in no significant modulations.