Introduction

Metal-organic-Frameworks (MOF) have become a centerpiece of the research on porous materials, building upon a tradition of research often centered around Zeolites. The large surface area and pores allow for novel applications such as physisorption for storage or filtering—both in gaseous1,2 and solvent environments3,4, hosting catalytic processes5 or innovative sensing mechanisms6. Compared to inorganic zeolites found in similar applications, MOFs are characterized by a mesostructural arrangement of metal nodes and organic linker-molecules, which form a network. While these can mimic the network topology of zeolites, such as in the ZIF-family of MOFs7, continuous research has allowed for an ever wide range of structures made possible by building block-like attachment chemistries of linker molecules on metal-clusters8,9. Once a working experimental mechanism has been established to create a MOF from a specific set of precursor molecules, the subsequent modification of linker precursors allows for a rapid combinatorial increase of possible structures with varying properties10.

For standardized theoretical experiments across this diversity of structures, computational scientists have started to collate datasets ready for high-throughput computation. The earliest effort was the CoreMOF dataset11,12 created from structures deposited in the Cambridge Structural Database (CSD)13. The QMOF database significantly improved on this, ensuring data provenance and proper deduplication of the CSD-data14,15 while also adding structures from the growing collections of hypothetical MOFs16,17,18. The latter idea is fully embraced in the MOFX19 and ARC-MOF20 projects, which both collate and standardize structures across databases of hypothetical MOF-structures and zeolites.

Typically, high-throughput studies built on these databases target the sorption capacities of the structures for a set of standard, commercially relevant gases (e.g. CO2, N2, H2), which are computed via time-consuming grand-canonical molecular mechanics simulations21. These simulations are typically performed using generic force field parameters, empirical partial charge models for coulombic interactions as well as rigid framework structures22. However, the fidelity of this approach is hampered by the accuracy of available classical force fields23,24 as well as the rigid framework assumption, given that experiments show that properties can change drastically by framework flexibility and naturally occurring defects25,26. Direct surrogate modeling using recent Machine Learning (ML) methods circumvents the cost of molecular mechanics simulations, but the underlying classical force field data limits the accuracy of these ML estimators27,28,29.

ML potentials promise significantly increased accuracy compared to classical force fields30,31,32,33 and are increasingly used as a drop-in replacements in molecular mechanics simulations34,35,36,37,38. Encouraging first results in MOF applications39 and growing evidence that with increasing system size, separating the interactions into a short-range ML potential component and a classical long-range electrostatics component is beneficial to improve accuracy and computational efficiency40,41,42, emphasize the importance of a reliable partial charge assignment modeling mechanism. Standalone, such a model can be used for diverse purposes, ranging from computing observables, such as dipole momenta for small molecules43,44, to replacing older empirical charge models used in REAX-FF-MD45. With an appropriate loss, the model can also be trained end-to-end to model potential energy surfaces for ionic materials46,47.

Recent work has shown that ML partial charge predictors can also be used to replace computationally expensive density functional theory (DFT) computations for MOFs48,49,50. However, due to the high dimensionality of chemical space, achieving a sufficient training data coverage by labeling randomly generated structures tends to be computationally prohibitive. This applies particularly to the context of screening for compounds, where the ML model needs to predict the labels for parts of chemical space, where by definition, there are no experimental or simulation data yet51. Active learning52,53 (AL) promises to efficiently generate diverse training datasets by only labeling configurations for which the model is uncertain, maximizing the information content per structure to reduce the required amount of labeled data significantly. To achieve this goal, AL builds the training data in an iterative manner by screening for high uncertainty inputs, labeling them and re-training the model on the extended training data. Consequently, AL efficacy critically depends on the quality of the employed uncertainty quantification (UQ) scheme to estimate the prediction error. For state-of-the-art graph neural network (GNN) surrogate models, popular UQ schemes include the Deep Ensemble method54,55, stochastic-gradient Markov chain Monte Carlo (SG-MCMC)56,57,58,59 and Dropout Monte Carlo60,61 (DMC). However, the former two methods are inefficient for AL given that they require retraining of several models at each AL iteration.

In this work, we investigate the efficacy of DMC for AL of MOF partial charges. To that end, we predict partial charges using a charge neutrality-enforcing48 GNN model, which we augment with Dropout layers to enable UQ via DMC. DMC represents a computationally efficient UQ scheme in an AL setting given that only a single parameter set needs to be re-trained at each AL iteration. We showcase the efficacy of DMC-based AL by training the GNN on the QMOF database and comparing its performance with an optimal AL oracle and a random baseline. Beyond AL, DMC can assess the model validity in the face of novel datapoints – allowing practitioners to estimate the expected error of the prediction. To evaluate the generalization and UQ capability of the obtained GNN under distribution shift, we benchmark the model on a subset of ARC-MOF and IZA-Zeolite.

Results

Active learning scheme

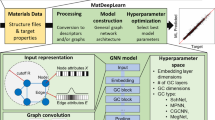
Figure 1a visualizes the AL pipeline used to train the GNN partial charge prediction model. The GNN enforces charge neutrality and features Dropout62 with a probability of p = 10% at all linear layers to enable UQ via DMC60 (more details in the methods section). We split the available training data into two sets: An initially small labeled set and an initially large pool set that is considered to be unlabeled. The AL cycle starts by training the GNN on the labeled set. Afterwards, we evaluate the uncertainty of the model with respect to all MOFs in the pool set. To this end, we predict the partial charges q associated with the atoms of each MOF for D = 8 different random Dropout configurations to estimate the mean μ and standard deviation σ across the D different predictions as

$${{{\boldsymbol{\mu }}}}=\frac{1}{D}\mathop{\sum }\limits_{d=1}^{D}{{{{\bf{q}}}}}_{d}\quad ;\quad {{{\boldsymbol{\sigma }}}}=\frac{1}{D-1}\mathop{\sum }\limits_{d=1}^{D}\sqrt{{({{{{\bf{q}}}}}_{d}-{{{\boldsymbol{\mu }}}})}^{2}}\,,$$
(1)

where qd are the predicted partial charges corresponding to Dropout configuration d.

Fig. 1: Graph neural network training and testing.
figure 1

a Active learning scheme to train a partial charge prediction graph neural network. Dropout Monte Carlo60 is used to compute the standard deviation (SD). b Test of generalization capabilities of partial charge predictions and uncertainties of the trained model under distribution shift.

Full size image

From the predicted standard deviation σ for each atom, we compute the average standard deviation of each MOF

$${\delta }_{{{{\rm{MOF}}}}}=\frac{1}{{N}_{{{{\rm{atoms}}}}}}\mathop{\sum }\limits_{k=1}^{{N}_{{{{\rm{atoms}}}}}}{\sigma }_{k}\,,$$
(2)

where Natoms is the number of atoms in the MOF. This allows to select the 16 MOFs with the largest δMOF in the pool set. As an alternative to δMOF, the MOFs could also be selected based on the maximum σk. Afterwards, we retrieve the labels of the selected MOFs, which emulates computing partial charge labels via DFT in practice. The newly labeled MOFs are added to the labeled set and retraining closes the AL loop. Training ends after a pre-defined accuracy threshold is reached or the whole pool set has been added to the labeled set. Refer to the methods section for a full set of AL hyperparameters.

After finishing training, the goal is to test the performance of the obtained model and its uncertainty estimates under the realistic scenario of distribution shift. To this end, we benchmark the model with respect to three datasets distinct from the training data (Fig. 1b): first, structurally bigger MOFs from the same distribution, second, MOFs from a different distribution and last, Zeolites representing related, but different structures.

Datasets

We deploy v13 of the QMOF dataset (as documented on the project homepage: https://github.com/Andrew-S-Rosen/QMOF/blob/main/updates.md), which contains 20375 MOFs with 77 different atom types. To test the generalization capabilities of the obtained NN model with respect to large structures of the same distribution, we hold-out all MOFs with more than 100 atoms (Fig. 2a). Given that GNNs cannot be expected to accurately model atoms that are not contained in the training data, we remove all MOFs containing atom types that occur less than 10 times in the < 100 atom MOF data subset. Consequently, the number of atom types reduces to 74, the set of small MOFs is reduced by 4 to 11173 and the set of large MOFs is reduced by 42–9156. Finally, we obtain the training dataset by applying a random 80%–8%–12% training-validation-test split to the small MOF dataset.

Fig. 2: QMOF v13 dataset statistics.
figure 2

a Distribution of the number of atoms per MOF in the QMOF dataset. The black dashed line indicates the split at 100 atoms between the small and large subsets. b Distribution of atom types in the QMOF dataset.

Full size image

To further evaluate the model performance with regards to inputs from a different distribution of MOFs, we consider the ARC-MOF database20. The database collates structures from 14 pre-existing datasets and includes additional synthetic structures generated with pormake17. We neglected the ARC-MOF databases 12 and 14 to minimize the overlap with the QMOF dataset to create real-world out-of-sample distributions. We chose a stratified sampling scheme that selects a minimum of 5% or a maximum of 20 structures per database to distinguish performance discrepancies among distinct datasets. We have included further comparisons illustrating the difference between these distributions in the Supplementary Figs. 1–3. Finally, we benchmark our model on 20 randomly selected structures from the IZA-Zeolite dataset acquired via MOFX-DB19. Zeolites have a different atomic structure than MOFs, but are commonly used in similar application areas, providing a challenging benchmark for generalization. In order to maintain consistency with the QMOF dataset, we computed partial charge labels of the structures sampled from ARC-MOF and IZA-Zeolite using the DFT settings used in QMOF as outlined in the methods section.

Evaluation metrics

Due to the chemical structure of MOFs, the majority of atoms correspond to organic linkers. Only four atom types (H, C, N, O) constitute 92.6% of the atoms in the QMOF dataset (Fig. 2b). Consequently, partial charge prediction for MOFs is a highly class-imbalanced ML problem.

The mean absolute error (MAE) is most commonly used to evaluate the performance of partial charge predictions for MOFs50, likely due to its straightforward interpretability. However, given the class imbalance of MOF atoms, MAE is dominated by organic linker atoms and is therefore an insufficient metric to evaluate model performance across the broad range of metal nodes. We therefore propose the per-species MAE (SMAE) as an alternative, interpretable metric to evaluate model performance for highly class-imbalanced datasets:

$${{{\rm{SMAE}}}}=\frac{1}{{N}_{{{{\rm{species}}}}}}\mathop{\sum }\limits_{i=1}^{{N}_{{{{\rm{species}}}}}}{{{{\rm{MAE}}}}}^{(i)}\quad {{{\rm{with}}}}\quad {{{{\rm{MAE}}}}}^{(i)}=\frac{1}{{N}_{{{{\rm{i}}}}}}\mathop{\sum }\limits_{k=1}^{{N}_{{{{\rm{i}}}}}}\left| {\mu }_{k}^{(i)}-{\hat{q}}_{k}^{(i)}\right| \,,$$
(3)

where Nspecies is the number of different atom types, Ni is the number of atoms of atom type i in the data (sub)set and \({\hat{q}}^{(i)}\) is the corresponding partial charge label. All atom types contribute equally to SMAE, effectively increasing the weight of metal nodes compared to the MAE.

Partial charge prediction performance

We evaluate the performance of the GNN for partial charge prediction by training the model on the full training data for 500 epochs without Dropout. On the test set, the resulting model yields MAE = 0.0083e and SMAE = 0.0339e, respectively (Table 1). This is in line with reported performance of partial charge prediction for MOFs in the literature with MAE values of 0.0192e50 and 0.025e48 on the CoRE MOF-2019 dataset12. Training the GNN with a Dropout probability of p = 10% yields test set errors of MAE = 0.0115e and SMAE = 0.0437e. We found that increasing p monotonously increases the test set errors (Supplementary Fig. 4). Consequently, we selected a small Dropout rate of p = 10% for the subsequent active learning task to minimize the model accuracy penalty from Dropout. Throughout the manuscript, we consider the mean over D = 8 Dropout configurations μ as the prediction of GNN models with Dropout. We choose this evaluation scheme because generating a single prediction by simply deactivating the Dropout layers at inference time yields significantly worse predictions across all our experiments.

Table 1 Predictive performance summary
Full size table

To set these metrics into perspective and judge whether the performance of the GNN is sufficient for surrogate modeling, we compare them to the error resulting from using a computationally less expensive DFT simulation with Γ-only sampling (as performed by Kancharlapalli et al.50) as a predictor for the results with a finer k-point grid (as in the work of Nazarian et al.63 and the QMOF dataset14). Using the 1260 identical structures that are shared between the works of Kancharlapalli et al.50 and Nazarian et al.63, we find MAE = 0.058e and SMAE = 0.136e. Accounting for possible outliers and noise, we set the target accuracy for our model to 50% of those values (Fig. 3). Thus, the achieved accuracy levels of our models with and without Dropout are more than sufficient for surrogate modeling.

Fig. 3: Active learning curves.
figure 3

Test set per-species mean absolute error (SMAE, (a)) and mean absolute error (MAE, (b)) as a function of the training set size for the Dropout Monte Carlo active learning (AL) scheme, the AL oracle benchmark and the random selection baseline compared to the density functional theory-derived accuracy target.

Full size image

Active learning

The goal of AL is to train a ML model that achieves the target accuracy while requiring the least amount of labeled training data. We benchmark the DMC-based AL method against a baseline scheme that randomly selects MOFs to be added to the training set as well as an AL oracle that uses the (in practice unavailable) true MAE of the MOF as the AL selection criterion:

$${{{{\rm{MAE}}}}}_{{{{\rm{MOF}}}}}=\frac{1}{{N}_{{{{\rm{atoms}}}}}}\mathop{\sum }\limits_{k=1}^{{N}_{{{{\rm{atoms}}}}}}| {\mu }_{k}-\hat{{q}_{k}}| .$$
(4)

As visualized in Fig. 3a, Dropout AL outperforms the random selection baseline, reducing the required amount of training data to reach the SMAE accuracy target to 13% of the training data compared to 24% for the random selection. As expected, the AL oracle outperforms the Dropout AL, reaching the DFT accuracy target at 6% of the training data. Nonetheless, at more than 14% of the training data, Dropout AL closes this gap and achieves the same performance as the oracle.

The increase in data efficiency of AL becomes more pronounced if duplicate structures exist in the dataset: We applied the AL pipeline to the original CoreMOF-201912 dataset containing 817 duplicate structures, which we detected via an improved de-duplication screening using the method described by Rosen et al.14. For this dataset, the random selection baseline required almost 4 times as many labeled samples as the Dropout AL scheme to reach the accuracy target (Supplementary Fig. 5). Interestingly, when considering MAE, AL appears to provide no significant benefit - even with the true error as uncertainty metric (Fig. 3b). The performance measured by MAE seems to be simply a function of the amount of training data, irrespective of the diversity of the structures.

Test set performance analysis

We analyze the performance of the GNN at the end of the active learning training (100% of the training data, termed AL GNN) on the small MOF test set. The AL GNN achieves a test set accuracy (MAE = 0.0136e, SMAE = 0.0325e) similar to the GNN directly trained on all the training data (Table. 1). Among organic linker atom types, the AL GNN features very small MAE only for hydrogen (MAE = 0.0063e). Interestingly, despite the large amount of atoms in the training data, the resulting MAE of carbon (0.0143e), nitrogen (0.0180e) and oxygen (0.0174e) atoms are in line with the MAE of many metal nodes (Supplementary Fig. 6). There are 4 atom types with large MAE > 0.1e: Hf, Nb, Fe, and, Sn (in error decreasing order). The large MAE of Hf and Nb can be explained by a lack of training data because both atom types appear less than 10 times in the training data. In contrast, there are 354 Fe and 233 Sn atoms in the training set. The cause for the large MAE of these more common metals is a topic for further research – a cursory visual inspection of 6 samples with individual per-atom-errors larger than 0.2e did not reveal any obvious commonalities, except 83% of samples exhibiting nonstandard-topologies that evaded classification with moffragmentor64.

Even though the per-species MAE of organic linker atoms is comparatively small, there are several atoms in the test data that exhibit very large errors (Fig. 4). Interestingly, these large error atoms tend to cluster together at similar DFT charge values (e.g. \(\hat{q}\,\approx\, 0.65\) e or \(\hat{q}\,\approx\, -0.15\) e for carbon and \(\hat{q}\,\approx\, -0.55\) e or \(\hat{q}\,\approx\, -0.95\) e for oxygen). The AL GNN appears to contain little information about these clusters given that the model predicts almost the full range of partial charges found for this atom type (see Supplementary Fig. 7 for dedicated parity plots for each organic atom type). Manual inspection of structures with very large error ( > 0.2e per atom) reveals several interesting features: First, 20 of the 24 structures exhibit both abnormal errors for oxygen and carbon, while 70% of those are classified as the lvt-topology. Visual inspection reveals that nearly every sample exhibits characteristic wire-like structures of carbon-atoms (see a sample in Supplementary Fig. 8), which appears to reduce the ability of our GNN to model this structure. Further research could help elucidate if these structures are physically feasible or if database screening criteria need to be refined.

Fig. 4: Test set parity plot.
figure 4

Comparison of the partial charge μ predicted by the GNN obtained via active learning with the DFT label \(\hat{q}\) for all atoms in the small MOF test set.

Full size image

Dropout Monte Carlo inference

Next, we investigate the generalization capabilities and the quality of uncertainty estimates of the AL GNN. The uncertainty estimate in Eq. (1) typically underestimates uncertainties for held-out data65. This is particularly true for the GNN in this work due to the small Dropout probability p = 10%. While a grid search over the Dropout rate could be performed to improve the calibration of the uncertainty estimates via a higher Dropout rate60,66, this higher rate would decrease the predictive accuracy (Supplementary Fig. 4). To avoid increasing the Dropout rate, we compute a calibrated uncertainty \(\tilde{{{{\boldsymbol{\sigma }}}}}\) by scaling the distribution of predicted uncertainties σ (Eq. (1) such that the variance in the uncertainty estimates matches the variance of the error on the validation set, as is common in the literature65:

$$\tilde{{{{\boldsymbol{\sigma }}}}}=\alpha * {{{\boldsymbol{\sigma }}}}\,\,\,{{{\rm{with}}}}\,\,\,\alpha =\sqrt{-\frac{1}{D}+\frac{D-3}{D-1}\frac{1}{{N}_{{{{\rm{val}}}}}}{\sum }_{l=1}^{{N}_{{{{\rm{val}}}}}}\frac{{({\mu }_{l}-{\hat{q}}_{l})}^{2}}{{\sigma }_{l}^{2}}}\,,$$
(5)

where Nval is the total number of partial charge labels \({\hat{q}}_{l}\) in the validation set and μl and σl are the DMC mean and standard deviations of the corresponding atom (Eq. (1)). The calibration of the AL GNN via Eq. (5) yields α = 1.504.

We investigate the model errors as well as the corresponding uncertainty estimates on three levels for each dataset: First, we analyse the MAE and SMAE for the whole dataset. Second, we compute MAEMOF (Eq. (4)) for each MOF to assess the performance of the UQ scheme to provide reliable uncertainty estimates for individual MOFs. To this end, we estimate MAEMOF via the mean calibrated standard deviation \({\tilde{\delta }}_{{{{\rm{MOF}}}}}\):

$${\tilde{\delta }}_{{{{\rm{MOF}}}}}=\frac{1}{{N}_{{{{\rm{atoms}}}}}}\mathop{\sum }\limits_{k=1}^{{N}_{{{{\rm{atoms}}}}}}{\tilde{\sigma }}_{k}\,.$$
(6)

Last, we investigate the absolute errors on the atom level \(| \mu -\hat{q}|\) to assess whether the calibrated standard deviation of the atom \(\tilde{\sigma }\) is able to identify regions of high error within the MOF.

On the test set, we find that the calibrated DMC can estimate aggregate error metrics well: While the mean \(\tilde{\sigma }\) of 0.0159e slightly overestimates the MAE of 0.0136e, the SMAE of 0.0354e is slightly underestimated with 0.0325e. On the level of single MOFs, the DMC uncertainty estimate is reliable in identifying large MAEMOF (Fig. 5a): The vast majority of MAEMOF errors are contained within the \(3{\tilde{\delta }}_{{{{\rm{MOF}}}}}\) credible interval and a correlation coefficient of 0.94 indicates a strong correlation between the two. However, this UQ performance does not translate to the atom level, where the correlation coefficient between \(| \mu -\hat{q}|\) and \(\tilde{\sigma }\) is only 0.67. In addition, many atoms are not contained in the \(3\tilde{\sigma }\) credible interval, which indicates that DMC cannot reliably predict error bounds for single atoms (Fig. 5b).

Fig. 5: Generalization performance.
figure 5

Parity plot of the absolute error of atoms \(| \mu -\hat{q}|\) and the mean absolute error of MOFs MAEMOF with the corresponding calibrated standard deviation \(\tilde{\sigma }\) and the calibrated mean standard deviation \({\tilde{\delta }}_{{{{\rm{MOF}}}}}\) for (a, b) the test set, (c, d) the held-out set of large MOFs with and without unknown atom types and (e, f) the ARC-MOF and IZA-Zeolite validation sets. The black dashed line indicates the optimal UQ estimate, where the UQ standard deviation matches the error. It separates regions of underconfidence (below) and overconfidence (above). The green dashed line visualizes the \(\pm 3\tilde{\sigma }\) credible interval, where points below the curve lie within the credible interval.

Full size image

Quality of dropout Monte Carlo under distribution shift

First, we assess the generalization capabilities of the GNN with respect to large MOFs of the same distribution by predicting the partial charges of MOFs with more than 100 atoms in the QMOF dataset (Fig. 2a). The resulting errors of MAE = 0.0114e and SMAE = 0.0468e demonstrate that the obtained GNN generalizes to large MOFs very well. Compared to the small MOF test set, the MAE is slightly lower, while the SMAE is slightly larger. We attribute the smaller MAE in parts to the larger ratio of organic linker atoms of 94.5% compared to 92.6% in the small MOF test set. The DMC uncertainty estimates also show similar properties: The MAE is slightly overestimated with a prediction of 0.0140e, the SMAE is slightly underestimated with a prediction of 0.0405e and the vast majority of MOFs are included in the \(3\tilde{\sigma }\) credible interval (Fig. 5c).

Next, we evaluate the prediction errors for MOFs with more than 100 atoms from the QMOF dataset that contain unseen atom types. As expected, with an MAE of 0.0316e and a SMAE of 0.1485, the prediction error is substantially larger compared to the case without unknown atom types. However, the corresponding UQ estimates for MAE and SMAE of 0.0141e and 0.0389e significantly underestimate the errors. On the MOF level, the errors are mostly contained within the \(3{\tilde{\delta }}_{{{{\rm{MOF}}}}}\) credible interval (Fig. 5c). However, the DMC UQ estimate does not assign large uncertainties to these MOFs. This becomes particularly clear at the atomic level (Fig. 5d): Even though, as expected, the predictions for atom types unknown to the model are highly inaccurate, the predicted uncertainty is comparatively small, resulting in significant overconfidence.

Last, we test the generalization capacity of the obtained GNN to different structures by evaluating the model on our DFT-labeled subsets of the ARC-MOF database20 and the IZA-Zeolite dataset. As expected, the prediction error increases in both cases due to the distribution shift: The model yields errors of MAE = 0.0239e, SMAE = 0.0696e and MAE = 0.0368e, SMAE = 0.0386e for the ARC-MOF and IZA Zeolite datasets, respectively. Considering that these errors remain in the range of the target accuracy, the generalization capabilities of the obtained GNN appear to be sufficient for its application under distribution shift in practice. In the case of ARC-MOF data, the UQ prediction underestimates these aggregate error metrics, with predictions of 0.0153e and 0.0369e for MAE and SMAE, respectively. Nonetheless, the vast majority of MOFs are contained in the \(3{\tilde{\delta }}_{{{{\rm{MOF}}}}}\) credible interval (Fig. 5e). In the case of IZA Zeolites, with uncertainty estimates of 0.0887e and 0.0914e for MAE and SMAE, DMC overestimates these aggregate error metrics. The DMC UQ clearly highlights that predictions for these Zeolites are uncertain (Fig. 5e), enabling practitioners to interpret obtained partial charge predictions accordingly or re-train the GNN with additional Zeolite training data. These findings are reflected at the atomic level, where DMC is overconfident in ARC-MOF prediction and slightly underconfident in IZA Zeolite predictions (Fig. 5f).

The Zeolite example with its large uncertainty predictions with respect to a shift in input structures is in stark contrast to the low uncertainty predictions with respect to unknown atom types (Fig. 5d). While the latter UQ error is more severe due to providing overconfident predictions, it can be easily avoided by only applying the model to MOFs with known atom types. The reason behind the different UQ results can be likely found in the GNN architecture: Evaluating DimeNet++33,67 on unknown atom types retrieves a randomly initialized atom type embedding from a look-up table, while changes in the input configuration propagate through the network via perturbations in the radial and spherical Bessel functions67. The variance in GNN activations introduced by DMC appears to be amplified more by unexpected radial and spherical Bessel function values than by unexpected atom type embeddings, leading to comparatively smaller uncertainty predictions in the latter case. However, further research is required to uncover the detailed mechanisms that cause the difference in UQ estimates.

Discussion

The obtained GNN model yields partial charge prediction errors significantly below our DFT-derived target, promoting its application to downstream computational studies: The GNN could be used out-of-the-box to extend the feature set of ML-based MOF screening studies such as those performed by Ren et al.68 – while only studied noble gases are studied, ML-predicted partial charges could help simulations with more complex molecules or provide additional, tabulated features to the gradient-boosting model. Additionally, the obtained GNN is suitable to predict partial charges for neural network potentials that model long-range electrostatic interactions40 or could be used as an enhancement for descriptor-based models69. Importantly, high-quality partial charge predictions can be obtained even under distribution shift, given that the GNN is able to generalize to large MOF structures, hypothetical MOFs and Zeolites, with errors below or close to their target values. This is particularly important for in-silico screening tasks, where the training and inference distributions are inherently different, representing a challenging setting for ML models trained on existing benchmark datasets51,70,71. Nonetheless, the GNN model could still be inaccurate in some cases, as shown for MOFs with unknown atom types, highlighting the need for reliable UQ.

This work demonstrated that DMC provides sensible uncertainty estimates: The \(3\tilde{\delta }\) credible interval contains the MAEMOF in the vast majority of cases, even for out-of-distribution settings, allowing practitioners to judge whether the expected error is sufficiently small for the application at hand. In addition, DMC is able to recognize zeolites as unknown structures. This is important because it indicates that MOFs with defects or with a perturbed framework might also be recognizable. On the other hand, this work has also revealed some shortcomings of DMC: First, adding Dropout to linear layers in GNNs tends to decrease predictive accuracy for larger Dropout probabilities. Second, in order to obtain the most accurate results with a DMC-trained model, we found that simply deactivating all Dropout layers was insufficient. Hence, approximating the mean over multiple Dropout configurations is necessary, which increases the computational cost at inference time. However, it should be noted that inference is nonetheless several orders of magnitude faster than querying the DFT calculation. Retraining the GNN model without Dropout on the dataset obtained by AL would be a straightforward solution to these issues, avoiding any penalty on accuracy and obtaining predictions in a single forward pass. While the retrained model does not have UQ capabilities on its own, the DMC uncertainty estimates might be distilled into it via student-teacher learning72,73,74. Alternatively, Gaussian Processes are attractive models for UQ because they provide uncertainty estimates without computational overhead75. In particular, recent method developments such as Deep Kernel Learning76,77 and linear scaling Gaussian Processes using graph-based feature-extractors78 have the potential to increase the efficiency of UQ without compromising predictive performance compared to state-of-the-art GNNs. Benchmarking their performance, in particular in an AL context, against GNN baselines such as DMC60 and the Deep Ensemble method55 is an interesting direction for future research.

Our results show that UQ is not only important for trustworthy predictions, but also allows to train ML models efficiently using AL. However, the benefits of AL only become apparent if an evaluation metric is used that accounts for the strong class imbalance of MOFs, highlighting the importance of selecting appropriate evaluation criteria. In the context of MOFs, while DFT-labeled databases kept increasing in size over the past years11,12,14,20, they will never contain all possible MOF structures. Based on our emulated database-building experiment, where AL clearly outperformed the random selection baseline, AL could play an important role in constructing the next iteration of MOF databases, maximizing the information content per structure. In addition, AL may prove valuable in addressing deduplication problems in MOF datasets: These range from failed deduplication in widely used databases12 to the more subtle problem of different compounds containing the same structural motifs. AL may provide an elegant solution, as motifs with similar properties will be identified rapidly. MOF databases with broad structural coverage are the foundation to obtain transferable ML partial charge prediction models, paving the way towards accurate molecular modeling of MOFs, e.g. for in-silico material design.

Methods

Probabilistic GNN for partial charge prediction

To predict partial charges, we build on our custom DimeNet++33,67 implementation79 with default hyperparameters, which learns for each atom type an embedding vector. We augment the original backbone architecture via a scheme that enforces charge neutrality. Given that the output blocks of DimeNet++ predict per-atom scalars, we consider these scalars to be raw partial charges \({\bar{q}}_{j}\). In order to enforce charge neutrality, we subtract the average net charge of the MOF from each atom to obtain the final partial charges48

$${q}_{j}={\bar{q}}_{j}-\frac{1}{{N}_{{{{\rm{atoms}}}}}}\mathop{\sum }\limits_{k=1}^{{N}_{{{{\rm{atoms}}}}}}{\bar{q}}_{k}\,.$$
(7)

The performance of the simple charge neutrality approach in Eq. (7) has been shown to be similar to more sophisticated schemes available in the literature48.

Supplementary Fig. 9 shows the net charge per atom of the AL GNN for MOFs in the small MOF test set when deactivating the charge neutrality scheme. Given that eq. (7) corrects shifts in the net charge, the GNN mean net charge prediction becomes arbitrary. In the case of the AL GNN, the mean net charge per atom is shifted to − 0.0284e. The average charge redistribution per atom of the AL GNN is comparatively small with 0.0048e per atom.

To enable DMC, we apply Dropout to all output neurons of each linear layer in the DimeNet++ architecture across all Embedding, Interaction, Residual and Output blocks (see fig. 1 in the original manuscript67). In particular, we do not apply Dropout to the message passing connectivity, nor to the initial edge embedding vectors. This way, we leave the molecular graph representation unaltered and only introduce noise into the learned transformations.

Active learning hyperparameters

We initialize the labeled set with 89 randomly selected MOFs from the training data (1% of the overall training data). We select a batch size of 8 MOFs and initially train the GNN model for 1000 epochs on the labeled set. After adding newly labeled MOFs, we preferentially train on these data points given that the model is already trained on the remainder of the labeled set. To this end, we employ a two-step training procedure: First, we train the model for 200 epochs of the newly labeled data on mini-batches consisting of 2 newly labeled MOFs and 6 randomly drawn MOFs from the labeled set. This represents a trade-off between avoiding overfitting to the newly labeled data and improved computational efficiency due to preferential training. Second, we train the GNN for 3 more epochs on the full labeled set to ameliorate the bias towards newly labeled MOFs from the previous preferential training.

Density functional theory setup

For computing partial charge labels, we employ the Vienna ab initio Simulation Package (VASP)80 version 6.2.1 and chargemol v09_02_201781. Using version 54 of the Projector-Augmented-Wave (PAW) pseudopotentials, we perform simulations using the PBE-functional, a kinetic energy cutoff of 520 eV, Gaussian smearing for the band occupancies of 0.01 eV and an energy convergence criterion of 1e-6. We choose k-point sampling such that (#k-points ⋅ real space cell-vector) > = 24, in line with chargemol best practices. The partial charges are then assigned from the resulting scf-charge density using the Density Derived Electrostatic and Chemical (DDEC)-charges assignment scheme81. We verified that these settings reproduce the partial charges from the QMOF-settings to numerical accuracy.