Machine learning nonequilibrium electron forces for spin dynamics of itinerant magnets

Abstract

We present a generalized potential theory for conservative as well as nonconservative forces for the Landau-Lifshitz magnetization dynamics. Importantly, this formulation makes possible an elegant generalization of the Behler-Parrinello machine learning (ML) approach, which is a cornerstone of ML-based quantum molecular dynamics methods, to the modeling of force fields in adiabatic spin dynamics of out-of-equilibrium itinerant magnetic systems. We demonstrate our approach by developing a deep-learning neural network that successfully learns the electron-mediated exchange fields in a driven s-d model computed from the nonequilibrium Green’s function method. We show that dynamical simulations with forces predicted from the neural network accurately reproduce the voltage-driven domain-wall propagation. Our work also lays the foundation for ML modeling of spin transfer torques and opens a avenue for ML-based multi-scale modeling of nonequilibrium dynamical phenomena in itinerant magnets and spintronics.

Introduction

In the past decade, machine learning (ML) techniques have greatly impacted many areas of industry and scientific research. The introduction of ML methods to the physical sciences has produced many fruitful results as well as opened several promising directions^{1,2,3,4,5,6,7,8,9,10}. In particular, the utilization of ML models as universal approximations for high-dimensional functions has significantly improved the efficiency of complex numerical simulations^{11,12,13,14,15,16,17,18,19,20,21,22}. Perhaps the most prominent and successful application in this direction is the ML prediction of energy and forces in quantum molecular dynamics (QMD) simulations^{23,24,25,26,27,28,29,30,31,32,33,34,35,36}. Contrary to classical MD methods that are based on empirical force fields, the atomic forces in QMD are computed by integrating out electrons on-the-fly as the atomic trajectories are generated³⁷. Various many-body methods, notably the density functional theory, have been used for the force calculation of QMD. However, the fact that most of these electronic structure methods are computationally very expensive significantly restricts the accessible scales of atomic simulations. The ML model offers a promising solution to this computational difficulty by accurately emulating the time-consuming many-body calculations, thus offering the possibility of large-scale QMD simulations with the desired quantum accuracy.

The central idea behind the remarkable scalability of ML force-field models is the principle of locality, or the nearsightedness, of electronic matters^38,39, which, in the context of QMD simulations, assumes that the force acting on a given atom only depends on its immediate surroundings. A practical implementation of the ML model based on this principle was demonstrated in the pioneer work of Behler and Parrinello²³, and Bartók et al.²⁴. In this approach, the total energy of the system is partitioned as E = ∑_iϵ_i, where ϵ_i is called the atomic energy and only depends on the local environment of the i-th atom^23,24. The atomic forces are then obtained from derivatives of the predicted energy: F_i = − ∂E/∂R_i, where R_i is the atomic position vector. Crucially, the complicated dependence of atomic energy ϵ_i on its neighborhood is approximated by the ML model, which is trained on the condition that both the predicted individual forces F_i as well as the total energy E agree with the quantum calculations.

Also importantly, by focusing on the local energy ϵ_i, which, as a scalar, is invariant under symmetry transformations such as rotations, the symmetry properties of the system can be easily incorporated into the ML model in such Behler-Parrinello (BP) type schemes^23,24. This approach also ensures that the predicted forces are conservative, a property that is important for Born-Oppenheimber molecular dynamics simulations. The BP scheme has been generalized to improve Monte Carlo simulations of lattice models in condensed matter physics^40,41,42,43. Notably, ML force-field models based on the BP scheme have also been developed to enable large-scale Landau-Lifshitz dynamics simulations of quasi-equilibrium correlated electron magnets^44,45.

The fact that the atomic forces are conservative in the BP-type approach, however, also significantly limits its capability to represent forces due to highly nonequilibrium electrons, such as in systems under external drive. This is because the energy E is not a well defined concept in such open systems. The resultant nonequilibrium electronic forces often cannot be written as a derivative of an effective potential energy. A case in point is the current-induced force^46,47,48,49 in, e.g. the molecular junctions, which has been shown to be nonconservative. Another important example is the spin-transfer torque^{50,51,52,53,54} due to polarized electron current that plays a central role in nanomagnetism and spintronics. Consequently, it is unclear how all the well-developed machinery of ML techniques for quasi-equilibrium QMD can be applied to model the dynamics of electronic systems far from equilibrium.

In this paper, we propose a solution to this important problem in the context of quantum Landau-Lifshitz-Gilbert dynamics for itinerant magnets. We first show that general nonconservative forces in the Landau-Lifshitz equation can be expressed in terms of two scalar potentials. This formulation thus allows one to translate the prediction of exchange fields to that of two potential energies. Applying the locality principle, a generalized BP neural network is developed to predict two associated local energies, from which the forces acting on spins can be obtained through automatic differentiation. As discussed above, the scalar outputs also allow for an easier incorporation of symmetry into the ML models. Moreover, similar to the original BP-type schemes, our proposed ML approach enjoys the advantage of further physical constraints on the force prediction. As a demonstration, we apply our ML framework to model the exchange fields computed from the nonequilibrium Green’s function method on the s-d system, a well-studied model for itinerant magnets. We further show that voltage-driven propagation of magnetic domain-walls can be accurately reproduced based on forces predicted by the trained neural-network model.

Results

Generalized potential theory

The dynamics of a magnetic system is described by the Landau-Lifshitz-Gilbert (LLG) equation^55,56:

$$\frac{d{{{{\bf{S}}}}}_{i}}{dt}=-\gamma {{{{\bf{S}}}}}_{i}\times {{{{\bf{H}}}}}_{i}+\alpha {{{{\bf{S}}}}}_{i}\times \frac{d{{{{\bf{S}}}}}_{i}}{dt},$$

(1)

where γ is the gyromagnetic ratio, α is an effective damping parameter, and H_i is a local magnetic field. In analogy with the molecular dynamics, this local electron-mediated exchange field can be viewed as a force acting on spin S_i. For a conservative exchange field, this local field is given by H_i = − ∂E/∂S_i, where E = E({S_i}) is the energy of the system which is either conserved or, in the presence of dissipation, decreases with time. Explicitly, the energy dissipation rate is $dE/dt=-\frac{\alpha }{\gamma }{\sum }_{i}{(d{{{{\bf{S}}}}}_{i}/dt)}^{2}$. Consequently, magnetization dynamics in an open system where energies can be pumped into spins from external sources is beyond the LLG equation governed by a conservative force.

As noted above, the nonequilibrium electronic forces are often nonconservative and cannot be expressed as derivatives of a single potential energy E. As a result, the BP method cannot be directly applied to model the nonequilibrium forces. An alternative approach is ML models that directly predict the nonconservative vector force H_i^57,58. However, besides the difficulty of incorporating the spin-rotation symmetry with a vector output, ML force-field model without additional energy constraints is prone to overfitting and hence less accurate. Indeed, in the so-called gradient-domain ML force-field models, additional constraint is introduced to ensure a curl-free conservative force field^57,58 for quasi-equilibrium electron systems.

For nonconservative forces originating from out-of-equilibrium electrons, there is no constraint on the force-field or the total energy. In order to impose similar physical conditions based on the potential theory, here we derive a general expression for the exchange fields acting on spins in terms of multiple scalar potentials. We first note that one of the most crucial features of the LLG dynamics is the preservation of the spin length, i.e. ∣S_i(t)∣ is a constant. The most general dynamical equation that satisfies this constraint has the form

$$\frac{d{{{{\bf{S}}}}}_{i}}{dt}={{{{\bf{T}}}}}_{i}=-\gamma {{{{\bf{S}}}}}_{i}\times {{{\bf{V}}}}({{{{\bf{S}}}}}_{i}),$$

(2)

where T_i is the torque and V(S) defines a vector field on a unit sphere S². Applying the Helmholtz-Hodge theorem for the case of the S² domain^59,60,61, the vector field can be decomposed into the radial, gradient, and solenoidal components as:

$${{{\bf{V}}}}({{{\bf{S}}}})={{{\bf{S}}}}\,{{{\mathcal{R}}}}({{{\bf{S}}}})+{\nabla }_{s}\,{{{\mathcal{E}}}}({{{\bf{S}}}})+{\nabla }_{s}\times {{{\mathcal{G}}}}({{{\bf{S}}}}),$$

(3)

where ${{{\mathcal{R}}}},{{{\mathcal{E}}}}$ and ${{{\mathcal{G}}}}$ are three scalar functions of the spin S = (S^x, S^y, S^z). The surface gradient operator on a scalar function f(S) is

$${\nabla }_{s}f=\frac{\partial f}{\partial {{{\bf{S}}}}}-{{{\bf{S}}}}\left({{{\bf{S}}}}\cdot \frac{\partial f}{\partial {{{\bf{S}}}}}\right),$$

(4)

while the curl operator on the S² sphere is given by

$${\nabla }_{s}\times f={{{\bf{S}}}}\times \frac{\partial f}{\partial {{{\bf{S}}}}}.$$

(5)

Here $\frac{\partial f}{\partial {{{\bf{S}}}}}={\sum }_{\alpha = x,y,z}\frac{\partial f}{\partial {S}^{\alpha }}$ is the normal gradient in three dimensions, without the restriction ∣S∣ = constant.

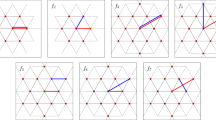
Since the radial component, which is parallel to the spin direction, does not contribute to the torque T_i, the radial function ${{{\mathcal{R}}}}$ behaves as a gauge transformation, which has no physical effects on the spin dynamics. This implies that one can define a physical exchange field H consisting of only the gradient and solenoidal components in the expansion Eq. (3), i.e. ${{{\bf{H}}}}={\nabla }_{s}\,{{{\mathcal{E}}}}({{{\bf{S}}}})+{\nabla }_{s}\times {{{\mathcal{G}}}}({{{\bf{S}}}})$. On the other hand, compared with the surface gradient ∇_s, the normal gradient ∂/∂S produces an additional radial component, which can then be gauged away, i.e. the difference between ${\nabla }_{s}{{{\mathcal{E}}}}$ and $\partial {{{\mathcal{E}}}}/\partial {{{\bf{S}}}}$, according to Eq. (4), is a radial vector field, which again does not contribute to the spin dynamics. Consequently, the most general exchange field in the LLG equation can be expressed in terms of the two scalar fields as

$${{{{\bf{H}}}}}_{i}=-\frac{\partial {{{\mathcal{E}}}}}{\partial {{{{\bf{S}}}}}_{i}}-{{{{\bf{S}}}}}_{i}\times \frac{\partial {{{\mathcal{G}}}}}{\partial {{{{\bf{S}}}}}_{i}}={{{{\bf{h}}}}}_{i}^{{{{\rm{eq}}}}}+{{{{\bf{h}}}}}_{i}^{{{{\rm{neq}}}}}.$$

(6)

By analogy with the conservative force, the first term is called the quasi-equilibrium exchange field. The second term which comes from the curl-field is denoted as the nonequilibrium exchange field; see Fig. 1. The generalized LLG equation then reads

$$\frac{\partial {{{{\bf{S}}}}}_{i}}{\partial t}=\gamma \,{{{{\bf{S}}}}}_{i}\times \frac{\partial {{{\mathcal{E}}}}}{\partial {{{{\bf{S}}}}}_{i}}+\gamma \,{{{{\bf{S}}}}}_{i}\times \left({{{{\bf{S}}}}}_{i}\times \frac{\partial {{{\mathcal{G}}}}}{\partial {{{{\bf{S}}}}}_{i}}\right)+\alpha {{{{\bf{S}}}}}_{i}\times \frac{\partial {{{{\bf{S}}}}}_{i}}{\partial t},$$

(7)

The first term describes the conventional precessional dynamics in Eq. (1) with the scalar potential ${{{\mathcal{E}}}}$ now playing the role of an effective conservative potential. Importantly, while the third Gilbert term accounts for universal dissipation of the energy ${{{\mathcal{E}}}}$, the second toroidal term can represents dynamical processes of both energy loss and gain. For example, by setting the potential ${{{\mathcal{G}}}}=-\lambda {{{\mathcal{E}}}}$, where λ is a positive parameter, the second term corresponds to a dissipation term introduced in LL’s original work⁵⁵. On the other hand, the nonequilibrium Slonczewski-Berger spin-torque^50,51 can also be expressed by the second term in Eq. (7) by identifying the vector ${{{{\boldsymbol{m}}}}}_{i}=-\partial {{{\mathcal{G}}}}/\partial {{{{\bf{S}}}}}_{i}$ as the magnetization of the fixed layer in a magnetic tunnel junction.

Fig. 1: The Helmholtz-Hodge of vector fields on a sphere.

A tangential vector field on a sphere can be decomposed into (a) the curl-free component ${\nabla }_{s}\,{{{\mathcal{E}}}}$ and (b) the divergence-free component ${\nabla }_{s}\times {{{\mathcal{G}}}}$. (c) shows the gradient field ${{{{\bf{h}}}}}_{i}^{{{{\rm{eq}}}}}=-\partial {{{\mathcal{E}}}}/\partial {{{{\bf{S}}}}}_{i}$, which can be viewed as a quasi-equilibrium exchange field, and the curl-field ${{{{\bf{h}}}}}_{i}^{{{{\rm{neq}}}}}=-{{{{\bf{S}}}}}_{i}\times \partial {{{\mathcal{G}}}}/\partial {{{{\bf{S}}}}}_{i}$, which corresponds to the nonequilibrium force, and their respective torques ${{{{\bf{T}}}}}_{i}^{{{{\rm{eq}}}}}={{{{\bf{h}}}}}_{i}^{{{{\rm{eq}}}}}\times {{{{\bf{S}}}}}_{i}$ and ${{{{\bf{T}}}}}_{i}^{{{{\rm{neq}}}}}={{{{\bf{h}}}}}_{i}^{{{{\rm{neq}}}}}\times {{{{\bf{S}}}}}_{i}$.

The fact that the generalized potential theory allows for dissipative mechanisms through the ${{{\mathcal{G}}}}$ term suggests a potential alternative formulation of thermostat. However, further investigation is required in order to consistently include the stochastic thermal fields in this formulation. On the other hand, by focusing the generalized potentials ${{{\mathcal{E}}}}$ and ${{{\mathcal{G}}}}$ on the modeling of electron-mediated exchange fields, a stochastic thermal field can be straightforwardly incorporated into the formulation based on conventional Gilbert damping with a consistent Langevin-type thermostat^62,63. Details of the stochastic LLG equation are discussed in the Methods section.

Machine-learning exchange-field model for LL dynamics

By expressing the general exchange fields in terms of the scalar potentials ${{{\mathcal{E}}}}$ and ${{{\mathcal{G}}}}$, which correspond to the quasi-equilibrium and nonequilibrium components, respectively, one can now generalize the BP-type NN scheme for the forces arising from out-of-equilibrium electrons. To this end, we first partition the two potential energies into local contributions, namely ${{{\mathcal{E}}}}={\sum }_{i}{\epsilon }_{i}$ and ${{{\mathcal{G}}}}={\sum }_{i}{\gamma }_{i}$. Based on the principle of locality^38,39, these two local energies ϵ_i and γ_i are assumed to depend only on the local magnetic environment ${{{{\mathcal{C}}}}}_{i}$ through two universal functions, i.e. ${\epsilon }_{i}=\varepsilon ({{{{\mathcal{C}}}}}_{i})$ and ${\gamma }_{i}=\chi ({{{{\mathcal{C}}}}}_{i})$ for a given electronic model. The overall dependence of the two potential energies on the spin configuration {S_i} of the system can be expressed as

$${{{\mathcal{E}}}}(\{{{{{\bf{S}}}}}_{j}\})=\mathop{\sum}\limits_{i}\varepsilon ({{{{\mathcal{C}}}}}_{i}),\quad {{{\mathcal{G}}}}(\{{{{{\bf{S}}}}}_{j}\})=\mathop{\sum}\limits_{i}\chi ({{{{\mathcal{C}}}}}_{i}).$$

(8)

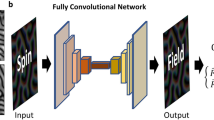
In practice, the magnetic environment ${{{{\mathcal{C}}}}}_{i}$ can be defined as the spin configuration within some cutoff radius R_c from the i-th spin, i.e. ${{{{\mathcal{C}}}}}_{i}=\left\{{{{{\bf{S}}}}}_{j}| \,| {{{{\bf{r}}}}}_{j}-{{{{\bf{r}}}}}_{i}| \le {R}_{c}\right\}$. As discussed above, the complex dependences of local energies on the local magnetic environment ${{{{\mathcal{C}}}}}_{i}$ are then approximated by a deep-learning NN as shown in Fig. 2.

Fig. 2: A scalable neural-network force-field model for out-of-equilibrium itinerant spin system and benchmark of force prediction.

a Schematic diagram of the neural-network model . A descriptor transforms the neighborhood spin configuration ${{{{\mathcal{C}}}}}_{i}$ to effective coordinates {G_ℓ} which are then fed into a NN. The two output nodes of the NN correspond to the local energy ${\epsilon }_{i}=\varepsilon ({{{{\mathcal{C}}}}}_{i})$ and ${\gamma }_{i}=\chi ({{{{\mathcal{C}}}}}_{i})$ associated with site-i. The corresponding total potential energies ${{{\mathcal{E}}}}$ and ${{{\mathcal{G}}}}$ are obtained from summation of these local energies. Automatic differentiation^65,66 is employed to compute the derivatives $\partial {{{\mathcal{E}}}}/\partial {{{{\bf{S}}}}}_{i}$ and $\partial {{{\mathcal{G}}}}/\partial {{{{\bf{S}}}}}_{i}$, from which the local exchange fields H_i are obtained according to the generalized force expression Eq. (6). The NN model is trained by datasets obtained from nonequilibrium Green’s function (NEGF) calculation for a driven s-d model. Panel b shows the ML predicted forces versus those from the NEGF calculation for the s-d model with exchange coupling J = 3.8t_nn; the blue and red data points correspond to the training and validation/test datasets, respectively. The inset shows the normalized distribution of the prediction error of the perpendicular components of the forces from the test dataset.

To ensure that symmetries of the original electron Hamiltonian are preserved in the two energy functions, a magnetic descriptor developed in our previous work⁴⁵ is employed to translate the local magnetic environment ${{{{\mathcal{C}}}}}_{i}$ into a set of feature variables {G_ℓ} that are invariant under symmetry operations of the system. In particular, for itinerant spin systems such as the well-studied s-d model, the global spin-rotation symmetry needs to be preserved in the ML force-field models. This SO(3) rotation symmetry can be manifestly maintained by using bond variables b_jk and scalar chirality χ_jkl as building blocks for the construction of the feature variables; they are defined as

$${b}_{jk}={{{{\bf{S}}}}}_{j}\cdot {{{{\bf{S}}}}}_{k},\quad {\chi }_{jkl}={{{{\bf{S}}}}}_{j}\cdot {{{{\bf{S}}}}}_{k}\times {{{{\bf{S}}}}}_{l}.$$

(9)

Effectively, this means that the two local energies are functions only of these bond/chirality variables in the neighborhood, e.g. ϵ_i = ε(b_jk, χ_jkl), where sites-j, k, and l are within the cutoff radius of the neighborhood.

The ML model also needs to respect the discrete lattice symmetries, such as described by the point group D₄ for the case of square lattice. To obtain the relevant invariant variables, we first note that the collection of bond/chirality variables {b_jk, χ_jkl} around the i-th spin form the basis of a high-dimensional representation of the D₄ group. This reducible representation of the magnetic environment is then decomposed into the fundamental irreducible representations (IR)⁶⁴. The basis of each IR ${f}_{r}^{{A}_{1}},{f}_{r}^{{A}_{2}},\cdots \,,{{{{\boldsymbol{f}}}}}_{r}^{E}$, where r enumerates the multiplicity in the IR in the decomposition, are proper linear combinations of the bond and scalar chirality variables. Finally, generalized coordinates {G_ℓ} that are invariant under lattice symmetry operations are obtained from the amplitudes and relative phases of these IR basis⁴¹. More details of the lattice descriptor can be found in the Methods Section.

The resultant feature variables {G_ℓ} are then fed into a fully connected NN, which in turn produces the two local energies ϵ_i and γ_i associated with the i-th spin; see Fig. 2. Applying the NN model to compute all the local energies, the two potential energies ${{{\mathcal{E}}}}$ and ${{{\mathcal{G}}}}$ are then obtained through Eq. (8). The local exchange fields H_i are computed from the derivatives of the two potentials via Eq. (6), where the two derivatives $\partial {{{\mathcal{E}}}}/\partial {{{{\bf{S}}}}}_{i}$ and $\partial {{{\mathcal{G}}}}/\partial {{{{\bf{S}}}}}_{i}$ can be efficiently and accurately computed using automatic differentiation techniques^65,66.

We emphasize that, as in ML-based interatomic potentials for quantum MD simulations, the ML energy model of Eq. (8) essentially provides a classical spin model for an underlying driven electronic systems. However, the energy and force calculations based on the highly nonlinear neural-network model is computationally more demanding compared with classical simulations of short-ranged empirical spin models^67,68. While computational efficiency of the neural net can be improved with GPU implementations, there are issues of limited memory storage, especially for models with a large cutoff radius. Nonetheless, the ML model is still significantly more efficient than the quantum calculations. Also importantly, the BP-type structure of the presented ML model allows for a linear-scaling implementation of the dynamical simulations.

It is worth noting that magnetic descriptors based on the above bond/chirality variables⁴⁵, strictly speaking, cannot be applied to electron-spin Hamiltonians with magnetic anisotropy, such as spin-orbit coupling. In such systems, the spin-rotation symmetry is coupled to the discrete lattice symmetry. Feature variables that are invariant under the combined symmetry group can still be obtained based on the group-theoretical method described above⁶⁹. However, for most s-d type models where the SU(2) spin-rotation symmetry is only slightly broken, the above descriptor is still a good approximation and a useful starting point for building more general feature variables. We note in passing that different approaches to magnetic descriptors have also been proposed in recent years^70,71, often in conjunction with MD simulations. While similar bond-variables are also proposed as descriptors⁷⁰, the inclusion of the scalar chirality χ_jkl in our model plays a crucial role in the stabilization of complex non-coplanar magnetic structures⁴⁵. Finally, off-lattice magnetic descriptors based on bond/chirality variables, which can then be used for combined LLG and MD simulations, are discussed in Ref. ⁶⁹.

Machine-learning for nonequilibrium Green’s function method

The above ML framework is general and can be used to represent exchange field in any nonequilibrium electron systems. As a demonstration of our approach, here we apply it to model the forces computed from the nonequilibrium Green’s functions (NEGF) method^72,73,74 for a driven s-d system^50,51,52. The s-d model is widely used in the study of spintronics and spin transfer torques for itinerant magnets. The large J limit of the s-d model, also known as the double-exchange model, plays an important role in the physics of colossal magnetoresistance observed in several manganites⁷⁵. Here we consider a square-lattice s-d system sandwiched by two electrodes in a capacitor structure shown in Fig. 3. The total Hamiltonian has two parts ${{{{\mathcal{H}}}}}_{{{{\rm{tot}}}}}={{{{\mathcal{H}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}+{{{{\mathcal{H}}}}}_{{{{\rm{res}}}}}$, where the first part is the s-d Hamiltonian,

$${{{{\mathcal{H}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}=-{t}_{{{{\rm{nn}}}}}\mathop{\sum}\limits_{\langle ij\rangle }\left({c}_{i\alpha }^{{\dagger} }{c}_{j\alpha }+{{{\rm{h}}}}.{{{\rm{c}}}}.\right)-J\mathop{\sum}\limits_{i}{{{{\bf{S}}}}}_{i}\cdot {c}_{i\alpha }^{{\dagger} }{{{{\boldsymbol{\sigma }}}}}_{\alpha \beta }{c}_{i\beta },$$

(10)

and ${{{{\mathcal{H}}}}}_{{{{\rm{res}}}}}$ describes the electrodes and reservoir degrees of freedom, as well as their coupling to the s-d model in the center. The effects of the reservoir fermions can be subsumed into a self-energy Σ^r(ϵ) in the retarded Green’s function:

$${{{{\bf{G}}}}}^{r}(\epsilon )={[\epsilon {{{\bf{I}}}}-{{{{\bf{H}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}-{{{{\boldsymbol{\Sigma }}}}}^{r}(\epsilon )]}^{-1},$$

(11)

where H_s−d is matrix representation of the s-d Hamiltonian in the site-spin (i, α) space; more details can be found in the Method Section. Next, the lesser Green’s function G^<, which is important for computing physical observables, is obtained using the Keldysh formula for quasi-steady electron states: G^<(ϵ) = G^r(ϵ)Σ^<(ϵ)G^a(ϵ), where the lesser self-energy Σ^< is related to the Σ^r through the dissipation-fluctuation theorem. For example, the on-site electron number is given by ${n}_{i}={\sum }_{\alpha }\langle {\hat{c}}_{i\alpha }^{{\dagger} }{\hat{c}}_{i\alpha }^{\,}\rangle ={\sum }_{\alpha }\int\frac{d\epsilon }{2\pi {{{\rm{i}}}}}{G}_{i\alpha ,i\alpha }^{ < }(\epsilon )$. The exchange fields acting on spins in Eq. (1) are obtained using the generalized Hellmann-Feynman theorem, and are explicitly computed from the lesser Green’s function^76,77,78,79

$${{{{\bf{H}}}}}_{i}=-\left\langle \frac{\partial {\hat{{{{\mathcal{H}}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}}{\partial {{{{\bf{S}}}}}_{i}}\right\rangle =J\mathop{\sum}\limits_{\alpha \beta }{{{{\boldsymbol{\sigma }}}}}_{\beta \alpha }\int\nolimits_{-\infty }^{+\infty }\frac{d\epsilon }{2\pi {{{\rm{i}}}}}{G}_{i\alpha ,i\beta }^{ < }(\epsilon ).$$

(12)

The above NEGF calculation is combined with the stochastic LLG dynamics to simulate the insulator-to-metal transition (IMT) of the s-d model driven by an external voltage⁷⁹. A small yet finite Langevin-type stochastic field is added to the local exchange field at every site to account for the thermal effects. A second-order algorithm is then used to integrate the LLG equation^80,81.

Fig. 3: Nonequilibrium Green’s function (NEGF) calculation for the s-d model driven by an external voltage.

a Schematic diagram of the driven s-d model in a metal-insulator-metal capacitor structure. The central region is described by the square-lattice s-d Hamiltonian in Eq. (10), while the two electrodes at left and right ends are shown here as modeled by simple square-lattice tight-binding model. An external voltage is applied to the two electrodes, giving rise to a difference in chemical potentials μ_L/R = μ₀ ∓ eV/2, where μ₀ is the chemical potential of the background reservoir. Panals b and c show the on-site electron number n_i and nearest-neighbor spin-spin correlation S_i ⋅ S_j, respectively, of a snapshot during the voltage-induced insulator-to-metal transition simulated by the NEGF-LLG method. The size of the square lattice is 30 × 24.

In the simulations of the voltage-induced IMT, the system is initially in an insulating antiferromagnetic (AFM) state with an energy gap ΔE_g = 2J. An external voltage V is applied to the two electrodes, which couple to the system at the left and right edges. When the chemical potential of the right electrode is lowered to the eigen-energies of the in-gap edge modes, an instability towards the ferromagnetic (FM) ordering is triggered as electrons are drained from the edge of the system into the electrode⁷⁹. This instability leads to the nucleation of the FM domains at the edge of the sample. The voltage-driven expansion of the FM domains transforms the system into the low-resistant metallic state. Panels (b) and (c) of Fig. 3 show the on-site electron number n_i and the nearest-neighbor spin-spin correlation b_〈ij〉 = S_i ⋅ S_j, respectively, of an intermediate state during the IMT. A rather sharp interface separating two domains of distinct electron densities is developed. The insulating AFM region is half-filled with exactly one electron per site, while the nucleated FM domains are characterized by low electron density and tend to be metallic.

The real-space NEGF calculation for a medium size lattice, e.g. less than 1000 spins, is already time-consuming by itself. This is mainly because the calculation of the retarded Green’s function G^r(ϵ) requires the inversion of a large matrix that has to be carried out for thousands of different energies ϵ; see Eq. (11). In the NEGF-LLG simulation of driven itinerant magnets, the above NEGF calculation has to be repeated at every time-step of the dynamical simulation. The resultant computational overhead is thus rather substantial. Even with 200 parallel cores, it often takes up to two weeks to perform a complete IMT simulation. As a result, only relatively small scale simulations with less than 1000 spins can be achieved even with highly parallelized programming⁷⁹. As discussed in the Introduction, by accurately emulating the expensive NEGF calculations, the ML approach to nonequilibrium electron forces offers a promising solution to overcome this difficulty of multi-scaling modeling.

Here we build a six-layer NN to implement the learning model shown in Fig. 2(a). The electronic exchange fields computed from the NEGF method are used to train the NN model based on our generalized force formula Eq. (6). A total of 3200 snapshots, each of which provides roughly 600 force data, are used for the training. Contrary to the standard BP method where both forces and total energy are included in the training of the NN model, the loss function in our case is entirely given by the mean squared error of the forces since the concept of total energy is not well defined for such open systems. Figure 2(b) shows the componentwise torques S_i × H_i predicted from our trained NN model versus the exact results. An excellent MSE of 8.97 × 10⁻⁶ is obtained from the trained NN model. The normalized distribution of the prediction error obtained from the validation dataset, shown in the inset of Fig. 2(b), is characterized by a rather small standard deviation of σ = 0.0014. More details of the ML training is discussed in the Method Section.

We note that the NN model is trained by dataset from NEGF-LLG simulations with a fixed external voltage eV = 3.2. As a result, it is designed to specifically learn the out-of-equilibrium electron states with this particular driving voltage, and cannot be used as an effective model for simulations of different V. Nonetheless, similar to ML force-field models for quantum MD simulations, our trained NN model is scalable, which means it can be used to simulate much larger systems with the same applied voltage. Moreover, the NN model is also transferrable in the sense that it can be used in ML-LLG simulations with different thermal fluctuations or classical magnetic disorder, such as random on-site anisotropy. In the latter case, more diverse and general datasets (with different temperatures or disorder realizations) have to be used for training the NN model. It is also possible to incorporate the driving voltage V as one of the inputs to the NN, assuming a smooth and continuous V-dependence of the exchange-fields. We will leave the development of such ML model for future studies.

Machine-learning spin dynamics simulations: Quasi-equilibrium vs Nonequilibrium torques

We next incorporate the NN exchange field model into the LLG dynamics for the simulation of the voltage-driven domain-wall propagation in the square-lattice s-d model. As discussed above, the kinetics of the nonequilibrium insulator-to-metal transition is essentially governed by the propagation of the FM-AFM domain walls. We focus our ML model on the force prediction of the interface region where the two distinct magnetic phases coexist. Figure 4(a) and (b) shows the propagation of domain walls obtained from the NEGF-LLG as well as the ML-LLG simulations on a 30 × 24 square lattice. The same initial state with a well-developed FM-AFM domain wall was used for both simulations. In the NEGF-LLG simulations, a small thermal noise is introduced which serves as a small perturbation to the unstable Néel order of the driven system. A Langevin-type thermostat, corresponding to a low temperature of k_BT = 0.01t_nn is employed in the stochastic LLG dynamics^62,63. On the other hand, the statistic error associated with the force prediction of the NN model, as shown in Fig. 2(b), can be treated as an effective thermal noise⁴⁵. Indeed, as the prediction error seems to be well approximated by a Gaussian distribution, its effect resembles the addition of normal-distributed random noise added to every site at each time-step in a Langevin thermostat⁶³.

Fig. 4: Benchmark and analysis of ML-LLG simulations of a driven itinerant magnet.

a and b Domain wall propagation in a s-d system driven by an external voltage eV = 3.2t_nn. Comparison between (a) NEGF-LLG simulations and (b) ML-LLG simulations. The lattice size is 30 × 24. The color bar indicates the local nearest-neighbor spin correlation b_ij = S_i ⋅ S_j. Blue (red) area corresponds to AFM (FM) domains. The NEGF-LLG simulation was carried out at a low temperature of k_BT = 0.01 t_nn, while the ML simulation was performed without Langevin noise. c Average position of FM-AFM domain, obtained from NEGF-LLG and ML-LLG simulations, as a function of time during the voltage-driven insulator to metal transition of the s-d model. d histogram of the ratio $| {{{{\bf{T}}}}}_{i}^{{{{\rm{neq}}}}}| /| {{{{\bf{T}}}}}_{i}^{{{{\rm{eq}}}}}|$ predicted by the NN model for the simulation of domain-wall propagation. The dashed lines are guide for eye. Here ${{{{\bf{T}}}}}_{i}^{{{{\rm{eq}}}}}={{{{\bf{S}}}}}_{i}\times \partial {{{\mathcal{E}}}}/\partial {{{{\bf{S}}}}}_{i}$ is the quasi-equilibrium torque, and ${{{{\bf{T}}}}}_{i}^{{{{\rm{neq}}}}}={{{{\bf{S}}}}}_{i}\times ({{{{\bf{S}}}}}_{i}\times \partial {{{\mathcal{G}}}}/\partial {{{{\bf{S}}}}}_{i})$ is the non-equilibrium torque in the generalized LLG equation. e histogram of the scalar product ${{{{\bf{T}}}}}_{i}^{{{{\rm{neq}}}}}\cdot {{{{\bf{h}}}}}_{i}^{{{{\rm{eq}}}}}$ obtained from the NN model for domain-wall propagation.

The domain-wall positions averaged over the transverse y-direction, obtained from LLG simulations using NEGF forces and ML-predicted forces, are plotted in Fig. 4(c) as functions of time. The two trajectories agree well with each other with a small discrepancy that can be attributed to the random Langevin noise in the LLG simulation and the force prediction error of the ML model. This overall agreement might indicate that the prediction error happens to mimic the small temperature used in the NEGF-LLG simulations. But more likely, this is an indication that thermal effect of this magnitude is not a dominant factor, but mainly serves as a seed to induce the instability of the Néel state.

A useful by-product of our NN model is the partitioning of the electron-mediated exchange fields into the quasi-equilibrium h^eq and nonequilibrium h^neq components according to the decomposition in Eq. (6). It is worth noting that such partitioning is often impossible in the microscopic approaches such as the NEGF calculation for the exchange field in Eq. (12). The introduction of these two potentials ${{{\mathcal{E}}}}$ and ${{{\mathcal{G}}}}$ is in fact similar in spirit to the partitioning of the total electronic energy into atomic or site energies in the original Behler-Parrinello ML model. These atomic energies also cannot be directly obtained from the DFT calculations. Yet the trained BP-type ML model could predict such local energies associated with individual atoms, thus providing useful information on the energy distribution of the atomic system.

From this decomposition, one can compute the quasi-equilibrium torques ${{{{\bf{T}}}}}_{i}^{{{{\rm{eq}}}}}={{{{\bf{h}}}}}_{i}^{{{{\rm{eq}}}}}\times {{{{\bf{S}}}}}_{i}$, as well as the nonequilibrium ones ${{{{\bf{T}}}}}_{i}^{{{{\rm{neq}}}}}={{{{\bf{h}}}}}_{i}^{{{{\rm{neq}}}}}\times {{{{\bf{S}}}}}_{i}$. Figure 4(d) shows the histogram of the ratio $| {{{{\bf{T}}}}}_{i}^{{{{\rm{neq}}}}}| /| {{{{\bf{T}}}}}_{i}^{{{{\rm{eq}}}}}|$ of these two torque components for spins in the vicinity of the AFM-FM domain walls. As expected, the driving force of the domain-wall propagation is dominated by the nonequilibrium exchange fields. As demonstrated in Fig. 1(c), the quasi-equilibrium torque ${{{{\bf{T}}}}}_{i}^{{{{\rm{eq}}}}}={{{{\bf{S}}}}}_{i}\times \partial {{{\mathcal{E}}}}/\partial {{{{\bf{S}}}}}_{i}$ is responsible for the precession motion of spins along contours of constant energy ${{{\mathcal{E}}}}$. The nonequilibrium torque ${{{{\bf{T}}}}}_{i}^{{{{\rm{neq}}}}}={{{{\bf{S}}}}}_{i}\times ({{{{\bf{S}}}}}_{i}\times \partial {{{\mathcal{G}}}}/\partial {{{{\bf{S}}}}}_{i})$, on the other hand, often points to a direction opposite to that of the Landau-Lifshitz damping torque ${{{{\bf{T}}}}}_{i}^{{{{\rm{damping}}}}}=\lambda {{{{\bf{S}}}}}_{i}\times {{{{\bf{T}}}}}_{i}^{{{{\rm{eq}}}}}$, where λ = γα/(1 + α²) is the effective damping coefficient, computed from the (quasi) equilibrium exchange field. This is confirmed by the histogram of the scalar product $({{{{\bf{T}}}}}_{i}^{{{{\rm{neq}}}}}\cdot {{{{\bf{h}}}}}_{i}^{{{{\rm{eq}}}}})$ obtained from the NN model for spins in the vicinity of the domain walls, which is shown in Fig. 4(e). The predominantly negative values of this scalar product indicate the nonequilibrium torques are mostly pulling the spins away from the local field direction ${{{{\bf{h}}}}}_{i}^{{{{\rm{eq}}}}}=-\partial {{{\mathcal{E}}}}/\partial {{{{\bf{S}}}}}_{i}$ due to the quasi-equilibrium potential, thus acting in a way similar to the so-called anti-damping torques^52,53,54.

Discussion

The machine-learning force-field models have revolutionized atomistic simulation methods which are crucial to several fields of biological and physical sciences. In particular, taking advantage of the nearsightedness property of electronic matter, the widely-used Behler-Parrinello scheme and other similar approaches allow one to implement transferrable and scalable ML force field models, thus enabling large-scale molecular dynamics simulations with the accuracy of the state-of-the-art quantum calculations. Yet, despite significant progress in recent years, the majority of research focus on conservative forces due to quasi-equilibrium electrons. This is partly because, by focusing on the prediction of local atomic energies, the BP-type approaches are restricted to forces which can be expressed as derivatives of an effective energy. An important challenge in this field is the generalization of the BP-type schemes to represent non-conservative forces originating from out-of-equilibrium electrons, such as those in a driven system.

Our work marks a crucial step toward ML modeling of nonequilibrium nonconservative force fields of functional electronic materials. Thanks to the special property that the magnitude of magnetization is conserved by the Landau-Lifshitz dynamics, a generalized potential theory is developed for both conservative and non-conservative forces for spin dynamics. More importantly, this formulation allows one to generalize the BP-type schemes to the ML modeling of electronic forces in highly nonequilibrium itinerant magnets. We demonstrate our approach by developing a neural network model that successfully predicts the electronic forces computed from the nonequilibrium Green’s function method for a driven s-d model. LLG simulations using the NN-predicted forces also accurately reproduce the voltage-driven domain-wall propagation.

The ML framework developed in this work can also be used to implement accurate and efficient modeling of spin-transfer torques (STT)^50,51,52,53, which plays a central role in the emerging field of spintronics. It is worth noting that most LLG simulations of magnetic systems involving STT are based on empirical formulas^{50,51,52,53,82,83,84}, which are similar to the empirical force-field models used in classical MD simulations. While LLG simulations with empirical STT formulas can be achieved on rather large systems, such classical simulations could not describe the subtle interplay between spins and electrons. On the other hand, although STT can be more accurately computed using the NEGF method, its combination with LLG dynamics simulations is computationally very demanding and has so far only been achieved with a hybrid classical-quantum implementation or applied to relatively small systems^{76,77,78,85,86,87,88,89}. We envision ML-based STT models will open an avenue to achieve large-scale dynamical simulations of magnetic textures and spintronic devices with the accuracy of nonequilibrium quantum methods.

While our work provides an elegant implementation of ML force models for general spin dynamics, it remains unclear whether and how similar approaches can be applied to the molecular force fields. The fact that a generalized BP method for spin dynamics is possible is because the exchange field is defined on the two-dimensional surface S² of a sphere. This suggests that a similar approach can be applied to the force fields of 2D molecular systems. Indeed, a general 2D force field can be decomposed as ${{{\bf{F}}}}(x,y)=-{\nabla }_{{{{\rm{2D}}}}}\,\phi +{\nabla }_{{{{\rm{2D}}}}}\times ({A}_{z}\hat{{{{\bf{z}}}}})$, where ∇_2D = (∂_x, ∂_y), and ϕ(x, y) and A_z(x, y) are two scalar functions. The ML framework developed here can be straightforwardly adopted to represent nonconservative and nonequilibrium forces for MD simulations of such driven 2D molecular systems. However, this approach cannot be directly applied to 3D systems as the representation of a general force field requires both a scalar and a vector potential: F = − ∇ ϕ + ∇ × A. One possible solution is to employ a NN model with a vector output. However, the preservation of spin rotation symmetry requires more sophisticated descriptors. Further work is required to develop a general ML force field model for QMD simulations of out-of-equilibrium electronic systems.

Methods

Stochastic Landau-Lifshitz-Gilbert dynamics

The NEGF-LLG simulations of the resistance transition are carried out at finite temperatures. To incorporate the stochastic thermal field into the LLG equation, an additional time-dependent term is added to the local exchange field H_i in Eq. (1), giving rise to the following stochastic LLG equation^62,63

$$\frac{d{{{{\bf{S}}}}}_{i}}{dt}=-\gamma {{{{\bf{S}}}}}_{i}\times \left({{{{\bf{H}}}}}_{i}+{{{{\boldsymbol{\zeta }}}}}_{i}\right)+\alpha {{{{\bf{S}}}}}_{i}\times \frac{d{{{{\bf{S}}}}}_{i}}{dt}.$$

(13)

There are two contributions to the local exchange fields: the deterministic exchange field H_i and a random thermal field ζ_i. The deterministic term is given by H_i = − ∂E/∂S_i for conservative field, or Eq. (12) for the non-conservative case of out-of-equilibrium system. For ML-LLG simulations, the deterministic exchange field H_i is obtained from the generalized potentials as shown in Eq. (6). The thermal fields at different sites are independent of each other and their time-dependence is modeled by a white noise with zero mean. Specifically they satisfy the following statistic properties

$$\begin{array}{rcl}\langle {\zeta }_{i}^{m}(t)\rangle &=&0,\\ \langle {\zeta }_{i}^{m}(t){\zeta }_{j}^{n}({t}^{{\prime} })\rangle &=&{\delta }_{ij}{\delta }_{mn}\delta (t-{t}^{{\prime} })\frac{\alpha {k}_{B}T}{\gamma }\end{array}$$

(14)

where m, n = x, y, and z denote the Cartesian components of the thermal fields. A second-order semi-implicit finite-difference method with special care taken to conserve the spin length is employed to integrate the stochastic LLG equation^80,81.

NEGF calculation of the exchange fields

In this section we outline spin dynamics with forces computed from the nonequilibrium Green’s function (NEGF) method. We consider a two-dimensional capacitor structure, shown in Fig. 2, described by a total Hamiltonian ${{{\mathcal{H}}}}={{{{\mathcal{H}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}+{{{{\mathcal{H}}}}}_{{{{\rm{res}}}}}$, where the two terms correspond to the s-d model in the center and the reservoir including the two electrodes at the two ends of the capacitor structure. The Hamiltonian of the s-d model is described in Eq. (10), and that of the reservoir is given by

$${{{{\mathcal{H}}}}}_{{{{\rm{res}}}}}=\mathop{\sum}\limits_{k,\alpha ,i}{\varepsilon }_{k}\,{d}_{i,k,\alpha }^{{\dagger} }{d}_{i,k,\alpha }-\mathop{\sum}\limits_{i,k,\alpha }{V}_{k,i}\left({d}_{i,k,\alpha }^{{\dagger} }{c}_{i,\alpha }+{{{\rm{h.c.}}}}\right).$$

(15)

Here d_i,α,k represents non-interacting fermions from the bath (i inside the bulk) or the leads (for i on the two open boundaries), α is the spin index, and k is a continuous quantum number. For example, k encodes the band-structure of the two leads.

As the s-d Hamiltonian is quadratic in the electron operators, which means there is no direct electron-electron interactions, it can be written as

$${{{{\mathcal{H}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}={\hat{{{{\bf{c}}}}}}^{{\dagger} }\,{{{{\bf{H}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}\,\hat{{{{\bf{c}}}}}.$$

(16)

where $\hat{{{{\bf{c}}}}}=\left({\hat{c}}_{1,\uparrow },{\hat{c}}_{1,\downarrow },\cdots \,,{\hat{c}}_{N,\uparrow },{\hat{c}}_{N,\downarrow }\right)$ is a vector of the electron annihilation operators, and we have introduced a “first-quantized" Hamiltonian H_s−d, which is a 2N × 2N matrix in the lattice site-spin space with the following matrix elements:

$${\left({{{{\bf{H}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}\right)}_{i\alpha ,j\beta }={t}_{ij}{\delta }_{\alpha \beta }-{J}_{{{{\rm{H}}}}}{\delta }_{ij}{{{{\bf{S}}}}}_{i}\cdot {{{{\boldsymbol{\sigma }}}}}_{\alpha \beta },$$

(17)

To simulate the time-evolution of the s-d model, we first note that the relatively slow dynamics of spins allows us to employ the adiabatic approximation, which is analogous to the Born-Oppenheimer approximation in quantum molecular dynamics. In this approximation, the electrons are assumed to quickly reach a quasi-steady state, which could be in quasi-equilibrium thermodynamically or out of equilibrium as in a driven system, with respect to the instantaneous spin configuration. The semiclassical or adiabatic dynamics of local spins in the s-d model is described by the stochastic LLG equation in Eq. (13). Computationally, the most crucial step is the calculation of the exchange field H_i. For a conservative force, e.g. due to electrons in quasi-equilibrium, the exchange field is given by the partial derivative of a potential energy: H_i = − ∂E/∂S_i, where $E=\langle {{{{\mathcal{H}}}}}_{{{{\rm{sd}}}}}\rangle ={{{\rm{Tr}}}}({\rho }_{{{{\rm{eq}}}}}\,{{{{\mathcal{H}}}}}_{{{{\rm{sd}}}}})$ is the energy of the quasi-equilibrium electron liquid^90,91. Often this is obtained using exact diagonalization or more efficient linear-scaling techniques such as the kernel polynomial method.

On the other hand, for an out-of-equilibrium quantum state $\left\vert \Psi \right\rangle$ such as the one driven by two electrodes in our case, the energy E of the system is not well defined. However, the exchange field can still be computed using the generalized Hellmann-Feynman theorem^76,77,

$${{{{\bf{H}}}}}_{i}=-\left\langle \Psi \left\vert \frac{\partial {{{{\mathcal{H}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}}{\partial {{{{\bf{S}}}}}_{i}}\right\vert \Psi \right\rangle ={J}_{{{{\rm{H}}}}}\,{\rho }_{i\alpha ,i\beta }(\{{{{{\bf{S}}}}}_{i}\})\,{{{{\boldsymbol{\sigma }}}}}_{\beta \alpha }.$$

(18)

Here we have introduced the single-particle density matrix ${\rho }_{i\alpha ,j\beta }(t)=\langle \Psi (t)| {c}_{j\beta }^{{\dagger} }{c}_{i\alpha }| \Psi (t)\rangle$. It is worth noting that this electron-induced nonequilibrium exchange field is related to the spin-transfer torques and current-induced phenomena such as tunneling magnetoresistance^50,51,52,53.

The general nonequilibrium density matrix ρ_iα,jβ(t) can be expressed in terms of the equal-time lesser Green’s function ${\rho }_{i\alpha ,j\beta }(t)={G}_{i\alpha ,j\beta }^{ < }(t,t)$, where the general two-time Green’s function, defined as ${G}_{i\alpha ,j\beta }^{ < }({t}_{1},{t}_{2})={{{\rm{i}}}}\langle \Psi (t)| {c}_{i\alpha }^{{\dagger} }({t}_{1}){c}_{j\beta }^{\,}({t}_{2})| \Psi (t)\rangle$, is computed using the NEGF method. First, assuming the various reservoir parts are in thermal equilibrium with their respective local chemical potentials, we integrate out these reservoir degrees of freedom and obtain the Fourier-transformed retarded Green’s function matrix for the central region.

$${{{{\bf{G}}}}}^{r}(\epsilon )={\left[\epsilon {{{\bf{I}}}}-{{{{\bf{H}}}}}_{{{{\rm{s}}}}-{{{\rm{d}}}}}-{{{{\boldsymbol{\Sigma }}}}}^{r}(\epsilon )\right]}^{-1},$$

(19)

where H_s−d is the first-quantized Hamiltonian matrix introduced in Eq. (17) and Σ^r is the matrix representation of the dissipation-induced self-energy; its explicit matrix elements are

$${\Sigma }_{i\alpha ,j\beta }^{r}(\epsilon )={\delta }_{ij}{\delta }_{\alpha \beta }\mathop{\sum}\limits_{k}\frac{| {V}_{i,k}{| }^{2}}{\epsilon -{\epsilon }_{k}+{{{\rm{i}}}}{0}^{+}}.$$

(20)

The resultant level-broadening matrix Γ = i(Σ^r − Σ^a) is diagonal with Γ_iα,iα = π∑_k∣V_i,k∣²δ(ϵ − ϵ_k). For simplicity, we assume flat wide-band spectrum for the reservoirs, which leads to a frequency-independent broadening factor with two different values Γ_lead and Γ_bath. Next, using the Keldysh formula for quasi-steady state, the lesser Green’s function is obtained from the retarded/advanced Green’s functions:

$${{{{\bf{G}}}}}^{ < }(\epsilon )={{{{\bf{G}}}}}^{r}(\epsilon ){{{{\boldsymbol{\Sigma }}}}}^{ < }(\epsilon ){{{{\bf{G}}}}}^{a}(\epsilon ),$$

(21)

and the lesser self-energy is related to the Σ^r/a through dissipation-fluctuation theorem:

$${\Sigma }_{i\alpha ,j\beta }^{ < }(\epsilon )=2{{{\rm{i}}}}\,{\delta }_{ij}{\delta }_{\alpha \beta }\,{\Gamma }_{i}\,{f}_{{{{\rm{FD}}}}}(\epsilon -{\mu }_{i}).$$

(22)

Here Γ_i = Γ_lead or Γ_bath depending on whether site-i is at the boundaries or in the bulk, and f_L,R(ϵ) = f_FD(ϵ − μ_L,R) are the Fermi-Dirac distribution functions. The local chemical potential μ_i = μ₀ for the bath, and μ_i = μ_L/R = μ₀ ∓ eV/2 for the two electrodes, where V is the applied voltage.

Given the retarded Green’s function G^r(ϵ) in frequency domain, the density matrix ρ_iα,jβ, which is the equal-time retarded Green’s function, is then given by the integral

$${\rho }_{i\alpha ,j\beta }\left(\{{{{{\bf{S}}}}}_{i}\}\right)=\int\frac{d\epsilon }{2\pi {{{\rm{i}}}}}{G}_{i\alpha ,j\beta }^{ < }\left(\epsilon ;\{{{{{\bf{S}}}}}_{i}\}\right),$$

(23)

for quasi-steady electron state. Here we have explicitly shown the dependence of both the Green’s function and the density matrix on the instantaneous spin configuration {S_i}. The density matrix is used in the computation of the exchange field Eq. (18) acting on spins.

Group theoretical method for lattice descriptor

The s-d model is characterized by two independent symmetry groups: the global SO(3) rotation symmetry and the point group symmetry of the lattice. Consequently, the feature variables or effective coordinates characterizing the magnetic environment ${{{{\mathcal{C}}}}}_{i}$ of the neighborhood need to be invariant under transformations of both symmetry groups. Here we outline the implementation of such a magnetic descriptor⁴⁵; more details can be found in Supplemental information. As discussed above, instead of directly using the spin vectors S_i as input, the spin-rotation symmetry can be preserved by using the scalar variables as building blocks for the magnetic descriptor. Two types of fundamental scalars that can be obtained from vector spins include the inner products, or bond variables, b_jk = S_j ⋅ S_k of a spin-pair, and the triple-product, also known as the scalar chirality, χ_jkl = S_j ⋅ S_k × S_l of a spin-triplet.

Next we construct feature variables that are invariant under the discrete point group symmetry, which is D₄ in the case of square lattice. The group-theoretical method provides a rigorous and systematic approach to obtain general invariants of a given symmetry group. The first step is to obtain the basis of irreducible representations (IRs) of the point group. In our case, the symmetry-related bond and scalar chirality variables constructed from the magnetic environment ${{{{\mathcal{C}}}}}_{i}$ form a finite-dimensional representation of the point group. They can be decomposed into IRs through proper combinations. For example, consider the four bonds b_m ≡ b_im between the center spin S_i and the four nearest neighbors S_m with m = 1, ⋯ , 4. The 1-dimensional IR A₁ is given by ${f}^{{A}_{1}}={b}_{1}+{b}_{2}+{b}_{3}+{b}_{4}$, while the 2-dimensional doublet IR is f^E = (b₁ − b₃, b₂ − b₄). More examples are given in the supplemental information. For convenience, we arrange the basis functions of a given IR in the decomponsition into a vector ${{{{\boldsymbol{f}}}}}_{r}^{\Gamma }=({f}_{r,1}^{\Gamma },{f}_{r,2}^{\Gamma },\cdots \,,{f}_{r,{D}_{\Gamma }}^{\Gamma })$ where Γ labels the IR, r enumerates the multiple occurrences of IR Γ in the decomposition, and D_Γ is the dimension of the IR. Given these basis functions, one can immediately obtain a set of invariants called power spectrum $\{{p}_{r}^{\Gamma }\}$, which are the amplitudes of each individual IR coefficients, i.e. ${p}_{r}^{\Gamma }={\left\vert {{{{\boldsymbol{f}}}}}_{r}^{\Gamma }\right\vert }^{2}$. However, feature variables based only on power spectrum are incomplete in the sense that the relative phases between different IRs are ignored. For example, the relative “angle" between two IRs of the same type: $\cos \theta =({{{{\boldsymbol{f}}}}}_{{r}_{1}}^{\Gamma }\cdot {{{{\boldsymbol{f}}}}}_{{r}_{2}}^{\Gamma })/| {{{{\boldsymbol{f}}}}}_{{r}_{1}}^{\Gamma }| | {{{{\boldsymbol{f}}}}}_{{r}_{2}}^{\Gamma }|$ is also an invariant of the symmetry group. Without such phase information, the NN model might suffer from additional error due to the spurious symmetry, namely two IRs can freely rotate independent of each other.

A more general set of invariants of a symmetry group is called the bispectrum coefficients⁹², which are triple products of the IR coefficients; the difference in the transformation properties of the three IRs is accounted for by the Clebsch-Gordon coefficients of the symmetry group. The power spectrum ${p}_{r}^{\Gamma }$ is a special subset of the bispectrum coefficients. It is also worth noting that the bispectrum coefficients are complete in the sense that they can be used to faithfully reconstruct the neighborhood configuration up to the symmetry operations. Indeed, it has been demonstrated that atomic descriptors for ML-based molecular dynamics can be obtained by applying the bispectrum method to the three-dimensional rotation group which is an intrinsic symmetry of interatomic interactions⁹³.

However, the number of bispectrum coefficients is often too large for practical applications, and some of them are redundant. Here we have implemented a descriptor that is modified from the bispectrum method⁴⁵. We introduce the reference basis functions ${{{{\boldsymbol{f}}}}}_{{{{\rm{ref}}}}}^{\Gamma }$ for each distinct IR of the point group. These reference basis are computed by averaging large blocks of bond and chirality variables, such that they are less sensitive to small changes in the neighborhood spin configurations. We then define the relative “phase" of an IR as the projection of its basis functions onto the reference basis: ${\eta }_{r}^{\Gamma }\equiv {{{{\boldsymbol{f}}}}}_{r}^{\Gamma }\cdot {{{{\boldsymbol{f}}}}}_{{{{\rm{ref}}}}}^{\Gamma }/| {{{{\boldsymbol{f}}}}}_{r}^{\Gamma }| \,| {{{{\boldsymbol{f}}}}}_{{{{\rm{ref}}}}}^{\Gamma }|$. The effective coordinates are then the collection of power spectrum coefficients and the relative phases: $\{{G}_{\ell }\}=\{{p}_{r}^{\Gamma }\,\,,\,\,{\eta }_{r}^{\Gamma }\}$. The various steps of the descriptor are summarized in the following

$${{{{\mathcal{C}}}}}_{i}\to \{{b}_{jk},{\chi }_{jmn}\}\to \{{{{{\boldsymbol{f}}}}}_{r}^{\Gamma }\}\to \{{p}_{r}^{\Gamma },{\eta }_{r}^{\Gamma }\}$$

(24)

The generalized coordinates {G_ℓ}, or feature variables characterizing the neighborhood spins, are then forwarded to the neural network which produces the local energies at its output node. For the cutoff radius R_c = 5a used in this work, there is a total of 539 bond/chirality variables in each neighborhood.

Neural network model and training

A six-layer NN model with four hidden layers composed of 1024 × 512 × 256 × 128 neurons is constructed and trained on PyTorch⁹⁴. A schematic diagram of the NN is shown in Fig. 2(a). The size of the input layer size is given by the number of feature variables G_ℓ, which is 539 in this work. The NN performs a series of linear transformations on the input neurons where the ReLU function⁹⁵ is used as the activation function between layers. The output layer consists of two neurons whose values correspond to the two local energies ϵ_i and γ_i. Since only the perpendicular component of the exchange field ${{{{\bf{H}}}}}_{i}^{\perp }$ enters the torque T_i = S_i × H_i that drives LL dynamics, the loss function is given by

$$L=\mathop{\sum }\limits_{i=1}^{N}{\left\vert {{{{\bf{H}}}}}_{i,\perp }^{{{{\rm{NEGF}}}}}-{{{{\bf{H}}}}}_{i,\perp }^{{{{\rm{ML}}}}}\right\vert }^{2}.$$

(25)

The parameter of the NN is optimized by the Adam stochastic optimizer⁹⁶ at a learning rate of 0.0001. For the training of the NN, 3200 snapshots from the NEGF-LLG simulations are used as the training dataset. A 5-fold cross-validation and early stopping regularization are performed to prevent overfitting. More details can be found in supplemental information.