Introduction

The Dzyaloshinskii–Moriya (DM) interaction1,2 is an antisymmetric exchange interaction that favors noncollinear alignment of magnetic moments and induces chiral magnetic order. In contrast to the Heisenberg exchange interaction that forms the basis of ferromagnetic and antiferromagnetic orders, the DM interaction is the source of unconventional magnetic textures. For example, spin spirals3, chiral Néel domain walls4,5, and skyrmions6,7,8 have been observed in bulk and thin-film magnets with strong DM interaction. Importantly, chiral Néel domain walls and skyrmions can be driven by the spin current that diffuses into the magnetic layer via the spin Hall effect of neighboring non-magnetic layers9,10,11,12,13. Such magnetic objects are topologically protected from annihilating each other14,15, a property that is absent in other magnetic systems. Current controlled motion of chiral Néel domain walls10,11 and skyrmions12,13 are thus attracting significant interest for their potential use in storage class magnetic memories16,17,18,19.

Recent studies have shown that the DM interaction emerges at the interface of the ferromagnetic layer and non-magnetic layer with strong spin–orbit interaction17. Although the underlying mechanism of such interfacial DM interaction is under debate, its size is sufficiently large to stabilize chiral domain walls and isolated skyrmions. To evaluate the strength and chirality of the DM interaction, i.e., the DM exchange constant, a number of approaches have been proposed. As many of the approaches make use of the dynamics of the magnetic system, for example, the current or field-induced motion of domain walls10,11,20,21, propagation of spin waves22, and current/field dependence of the magnetization reversal processes23,24, there are difficulties in accurately extracting the DM exchange constant. The difficulties arise in part because the value depends on the model used to describe the system. In addition, random pinning of domain walls (and spin textures), which originates from the magnetic anisotropy distribution within the magnetic thin film, influences magnetization dynamics and adds uncertainty in the determination of the DM exchange constant. Since there is almost no means to control (and evaluate) the magnetic anisotropy distribution, estimation of DM exchange constant relies on the given property of each system.

Magnetic domain structure at equilibrium is determined by minimization of magnetic energy of the system, which typically includes magneto-static, magneto-elastic, anisotropy, Heisenberg exchange, and DM exchange energies. The pattern of the magnetic domain structure, therefore, includes information of the DM exchange constant. Recent studies have shown that the radius of skyrmions allows the determination of its size13,25,26,27. As the size of the skyrmions is of the order of few tens of nanometers; however, it remains a significant challenge to obtain their images with typical laboratory equipment. Similarly, mapping the magnetization direction of magnetic domain walls, which are typically a few nanometers wide, requires state-of-the-art imaging techniques5,28.

Here, we show that the DM exchange constant can be simply extracted from a micrometer-scale magnetic domain image using pattern recognition and machine learning. A convolutional neural network is used to characterize the magnetic domain pattern. To train the neural network, a large number of images with different patterns that derive from a magnetic system with fixed material parameters are required. As it is extremely challenging to synthesize films with well-defined material parameters, here we use micromagnetic simulations to generate the images for supervised learning. Micromagnetic simulation is a widely used tool to study magnetic systems. The simulation is capable of returning images that resemble those obtained in the experiments13,29,30. The system is trained and tested using the images generated from the simulations. As a demonstration, we use the trained system to estimate the DM exchange constant from experimentally obtained magnetic domain images (see Fig. 1 for the procedure used). We show that the trained system can estimate not only the DM exchange constant, which is in good agreement with experiments, but also the distribution of the magnetic anisotropy energy, for which only a few experimental studies have been reported thus far31,32.

Fig. 1: Concept of the study.
figure 1

Micromagnetic simulations are used to generate thousands of training images. There are five relevant material parameters: \(M_s\), \(K_{{\mathrm{eff}}}\), \(A_{{\mathrm{ex}}}\), \(D\), and \(\sigma\). Here we vary \(D\) and \(\sigma\) in the simulations so that the system can learn domain patterns with different \(D\) and \(\sigma\). After the supervised training, we feed the system with an experimentally obtained image of magnetic domains to extract \(D\) and \(\sigma\).

Full size image

Results and discussion

Preparation of training and testing data sets

The training data set is generated using a homemade micromagnetic simulation code. See “Methods” for the details of the calculations. The magnetic anisotropy dispersion (\(\sigma\)) is defined as \(\sigma \equiv {\mathrm{{\Delta}}}K_{\mathrm{u}}/K_{\mathrm{u}}\), where \(K_{\mathrm{u}}\) is the magnetic anisotropy energy density and \({\mathrm{{\Delta}}}K_{\mathrm{u}}\) is its variation. We first generate training images with fixed \(\sigma\) (\(\sigma = 0.15\)), \(K_{\mathrm{u}}\), saturation magnetization (\(M_s\)), and exchange constant (\(A_{{\mathrm{ex}}}\)). The value of each parameter is chosen to mimic typical thin-film heterostructures33 (see Table 1). The DM exchange constant (\(D\)) is varied from 0 to 1.00 mJ m−2. The initial condition and the pattern of \(K_{\mathrm{u}}\) distribution are varied to generate 100,000 training images of the equilibrium magnetic state for a given parameter set with various values of D (see “Methods” and Supplementary Fig. 1 for the details). Exemplary images of the equilibrium magnetic state with different \(D\) are shown in Fig. 2a. The domain size tends to shrink with increasing \(D\), consistent with theoretical models13,25,26,27. Due to a non-zero \(\sigma\) which causes random pinning, it is difficult to identify a clear trend in the shape of the domains with varying \(D\).

Table 1 Summary of the material parameters used in micromagnetic simulations.
Full size table
Fig. 2: Training and validation of the neural network system.
figure 2

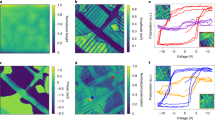
a Typical magnetic domain images calculated using micromagnetic simulations (the images are used for training). Dark and bright contrast represents the magnetization direction along the film normal. The DM exchange constant is varied from 0 to 0.90 mJ m−2: the corresponding value is indicated at the bottom right corner of each image. b The DM exchange constant (\(D^{{\mathrm{est}}}\)) estimated from the testing images are plotted as a function of D set in the simulations (\(D^{{\mathrm{set}}}\)). c Histograms of the \(D^{{\mathrm{est}}}\) for \(D^{{\mathrm{set}}} = 0.2,\,0.4,\,0.6,\,0.8,\,1.0\) mJ m−2. a–c \(\sigma\) is fixed to 0.15 in the simulations to generate the training/testing images. d Same with (a) except that, in addition to D, \(\sigma\) is randomly varied in the process of creating training images. The images shown are randomly chosen from a set of training images with fixed D but various \(\sigma\). The corresponding value of D is indicated at the bottom right corner of each image. e \(D^{{\mathrm{est}}}\) vs. \(D^{{\mathrm{set}}}\). f \(\sigma ^{{\mathrm{est}}}\) vs. \(\sigma ^{{\mathrm{set}}}\). d–f Both D and \(\sigma\) are varied in the simulations to generate the training/testing images. See Table 1 for the values of all material parameters.

Full size image

Model validation is performed with 10,000 testing images with different values of D created using the same code. \(D^{{\mathrm{set}}}\) corresponds to \(D\) used in the simulations to generate the testing images. The testing images are studied by the trained system: the estimated \(D\) returned from the system is denoted as \(D^{{\mathrm{est}}}\). The relation of \(D^{{\mathrm{set}}}\) vs. \(D^{{\mathrm{est}}}\) is shown in Fig. 2b. When \(D^{{\mathrm{set}}}\) is larger than ~0.05 mJ m−2, we find a linear relation between \(D^{{\mathrm{set}}}\) vs. \(D^{{\mathrm{est}}}\) with a root mean square (rms) error of ~0.046 mJ m−2. To show the distribution of \(D^{{\mathrm{est}}}\) more clearly, we plot the histogram of \(D^{{\mathrm{est}}}\) for five different values of \(D^{{\mathrm{set}}}\) (Fig. 2c). The standard deviation of each histogram is ~0.05 mJ m−2, consistent with the rms error of \(D^{{\mathrm{set}}}\) vs. \(D^{{\mathrm{est}}}\). These results show that the system cannot accurately determine \(D\) when \(D^{{\mathrm{set}}} \lesssim 0.05\) mJ m−2.

In experiments, it is typically the case that \(\sigma\) is not a known parameter. It is therefore more effective if one can determine both parameters, \(D\) and \(\sigma\), at once from a single magnetic domain image. We have thus created training images with both \(D\) and \(\sigma\) varied. On top of the changes in \(D\) (0–1.00 mJ m−2), we vary \(\sigma\) from 0 to 0.2. We generate 100,000 training images with various values of D and \(\sigma\), different initial condition and anisotropy distribution pattern. Figure 2d shows images of the equilibrium magnetic states with different \(D\) and \(\sigma\). As the value of \(\sigma\) is random here, we find almost no trend in the size as well as the shape of the domains with increasing \(D\). Although human eyes can hardly identify any pattern associated with changes in \(D\), the trained system does a surprising good job in detecting the difference. Again, we generate 10,000 testing images using the same code for model validation. In Fig. 2e, we show the \(D^{{\mathrm{set}}}\) dependence of \(D^{{\mathrm{est}}}\). Albeit the variation in \(\sigma\), \(D^{{\mathrm{est}}}\) scales \(D^{{\mathrm{set}}}\) with a rms error of ~0.045 mJ m−2, nearly the same with that of the training data set with a fixed \(\sigma\) (Fig. 2b). These results show that the trained system does not rely on the size of magnetic domains to determine \(D\): we infer that the curvature of the domains as well as the shape of the domain boundary play a role in the determination process25.

Interestingly, the trained system can independently determine the value of \(\sigma\) in addition to D. The estimated value of \(\sigma\) (\(\sigma ^{{\mathrm{est}}}\)) is plotted against the set value \(\sigma ^{{\mathrm{set}}}\) in Fig. 2f. As evident, the trained system provides an accurate estimation of \(\sigma\): the rms error is ~0.005. These results clearly show that a trained system can estimate multiple material parameters simultaneously from a single magnetic domain image. Provided that the parameters are not correlated, we consider the approach can be extended to estimate other parameters (e.g., \(K_{{\mathrm{eff}}}\), \(M_s\), \(A_{{\mathrm{ex}}}\)) as well.

Magnetic properties of the samples for pattern recognition

We next use the trained system to estimate \(D\) and \(\sigma\) from experimentally obtained magnetic domain images. The film of the samples used is: Si sub./Ta (d)/Pt (2.6 nm)/Co (0.9 nm)/MgO (2 nm)/Ta (1 nm). Details of sample preparation and characterization are described in “Methods”. The thickness of the Ta seed layer (d) is varied to change \(D\) of the films via modification of the (111) texture of the Pt layer (while attempting to minimize changes to other parameters). The magnetic easy axis of the films points along the film normal. The average \(M_s\) of the measured films is ~1445 kA m−1. The d dependence of \(K_{{\mathrm{eff}}}\), i.e., the effective magnetic anisotropy energy density defined as \(K_{{\mathrm{eff}}} = K_{\mathrm{u}} - \frac{{M_s^2}}{{2\mu _0}}\) (\(\mu _0\) is the vacuum permeability), is shown in Fig. 3c. The increase in \(K_{{\mathrm{eff}}}\) with increasing d is associated with the improvement of the texture of the Pt and Co layers.

Fig. 3: Experimental determination of the DM interaction.
figure 3

a Schematic illustration of the film structure, an optical microscope image of a representative device and a definition of the coordinate axes. b Switching field \(H_{\mathrm{c}}\) plotted as a function of \(H_x\) for Hall bars made from heterostructures with different Ta seed layer thickness (d). The vertical arrows indicate \(H_{{\mathrm{DM}}}\) obtained by fitting the data with model calculations24. The solid lines show the fitting results. c, d d dependence of the effective perpendicular magnetic anisotropy energy (\(K_{{\mathrm{eff}}}\)) (c) and the DM exchange constant (D) (d).

Full size image

The DM exchange constant is estimated using magnetic field-induced switching of magnetization24. A Hall bar is patterned from the films using conventional optical lithography. See Fig. 3a for a schematic illustration of the film structure, an optical microscope image of a representative device, and definition of the coordinate axis. We use the Hall voltage to probe the z component (i.e., along the film normal) of the magnetization via the anomalous Hall effect. To extract D, the easy axis switching field (\(H_{\mathrm{C}}\)) is studied as a function of in-plane magnetic field (\(H_x\)). Figure 3b shows the \(H_x\) dependence of \(H_{\mathrm{C}}\) for films with different d. As reported previously[24], in systems with non-zero \(D\), \(H_{\mathrm{C}}\) shows a sharp decrease with increasing \(|H_x|\) at \(H_x\sim H_{{\mathrm{DM}}}\), where \(H_{{\mathrm{DM}}}\) is the DM exchange field defined as \(H_{{\mathrm{DM}}} = D/(\mu _0M_s{\mathrm{{\Delta}}})\) (\({\mathrm{{\Delta}}} = \sqrt {A_{{\mathrm{ex}}}/K_{{\mathrm{eff}}}}\)). The data are fitted with a model calculation24 to obtain \(H_{{\mathrm{DM}}}\): the results are shown by the solid lines in Fig. 3b. The d dependence of \(D\) is plotted in Fig. 3d. We find \(D\) shows a sharp increase as d exceeds ~1 nm. We consider the texture of the Pt/Co interface plays a dominant role in defining D. The size of D when d exceeds ~1 nm is in agreement with past reports20,34,35,36 (see Supplementary Table 1 for values of D obtained in similar heterostructures).

Pattern recognition of magnetic domain images

The magnetic domain images of the films are acquired using a magnetic microscope equipped with a magnetic tunnel junction (MTJ) sensor39. We note that a more common Kerr microscopy can be used for the imaging. Here, we are limited by the size of the training images generated by micromagnetic simulations: to save computation time, we have used images with dimensions of ~2 × 2 μm2. Since the neural network is trained using these images, the spatial resolution of the imaging tool must be significantly better than ~1 μm, which excludes the use of conventional Kerr microscopy.

Typical magnetic domain images obtained using the microcopy are shown in Fig. 4a. Clearly, the size of the domains changes as d is varied. These images are fed into the trained system to estimate \(D\) and \(\sigma\). To mimic the experimental condition, \(M_s\) and \(K_{{\mathrm{eff}}}\) used in the simulations to generate training images are chosen from experiments and \(A_{{\mathrm{ex}}}\) is taken from past reports on similar systems37,38. Since \(K_{{\mathrm{eff}}}\) varies with d (see Fig. 3c), we use the lower (~0.24 MJ m−3) and upper (~0.37 MJ m−3) limits of \(K_{{\mathrm{eff}}}\) in the simulations. We have also included Langevin field in the simulation to emulate thermal fluctuation (see “Methods”).

Fig. 4: D and σ obtained from pattern recognition and machine learning.
figure 4

a Experimentally obtained magnetic domain images using a magnetic microscope equipped with a MTJ sensor. The bright and dark contrast represent magnetization pointing from and into the paper. The thickness of the Ta seed layer (d) is denoted in each image. b, c DM exchange constant (D) (b) and distribution of \(K_{\mathrm{u}}\) (\(\sigma\)) (c) estimated from the domain images using the trained system. Two different values of \(K_{{\mathrm{eff}}}\) are used in the simulations to generate the training images: the estimated values (D and \(\sigma\)) obtained from the trained systems are denoted using open and solid squares. The error bars show 95% confidence interval (see “Methods”). D from Fig. 3c is shown together by the red circles in (b).

Full size image

The value of \(D\) the trained system returned for each image is plotted against d in Fig. 4b. Interestingly, the d dependence of the estimated \(D\) is consistent with that of the experiments (red circles in Fig. 4b). Note that the magnitude of \(K_{{\mathrm{eff}}}\) does not significantly influence estimation of \(D\). Values of \(\sigma\) obtained from the images are plotted as a function of d in Fig. 4c. The size of \(\sigma\) estimated from the images can be compared to that obtained, for example, via measurements of the domain wall velocity distribution (\(\sigma \sim 0.15\))31 and magnetic hysteresis loops of a nano-patterned structure32. We find \(\sigma\) tends to monotonically decrease with increasing d. This is in sharp contrast to \(D\), which shows an abrupt increase when d exceeds ~1 nm. The monotonic change of \(\sigma\) with d is in accordance with that of \(K_{{\mathrm{eff}}}\) (Fig. 3c). Similar to \(K_{{\mathrm{eff}}}\), we infer that \(\sigma\) is related to the texture of the Pt/Co layer, however, in a different way than that of D. The stark difference in the d dependence of the estimated \(D\) and \(\sigma\) demonstrates that the trained system can identify multiple parameters independently as long as they are not correlated.

In summary, we have demonstrated that pattern recognition and machine learning can be applied to extract critical material parameters from a single magnetic domain image. In particular, we show that the DM exchange constant (D) and distribution of the magnetic anisotropy energy (\(\sigma\)), two key parameters that are difficult to assess experimentally, can be extracted from an image. The accuracy of the supervised learning in estimating D and \(\sigma\) are found to be ~0.05 mJ m−2 and ~0.005, respectively, which can likely be reduced with improved learning algorithms. As a proof-of-concept, we use the trained system to estimate D and \(\sigma\) of Co-based heterostructures using magnetic domain images obtained from a magnetic microscope. The estimated value of D is in good agreement with that extracted from experiments. This approach can be extended to estimate all relevant material parameters (e.g., \(M_s\), \(K_{{\mathrm{eff}}}\), \(A_{{\mathrm{ex}}}\),…) at once from a single magnetic domain image, which will significantly simplify materials research for magnetic memory and storage technologies.

Methods

Sample preparation and film characterization

Films are deposited using rf magnetron sputtering on a silicon substrate. The film structure is: Si sub./Ta (d)/Pt (2.6 nm)/Co (0.9 nm)/MgO (2 nm)/Ta (1 nm). A moving shutter is used to vary the thickness (d) of the Ta seed layer linearly across the substrate. d is varied from ~0 to ~3 nm across a 10-mm long substrate. The MgO (2 nm)/Ta (1 nm) serves as a capping layer to prevent oxidation of the Co layer. The saturation magnetization (\(M_s\)) of the heterostructure is studied using vibrating sample magnetometry (VSM). We take the average value of \(M_s\) for films with varying d.

The heterostructure is patterned into Hall bars using optical lithography and Ar ion etching. The length and width of the current channel of the Hall bar is ~60 μm and ~10 μm, respectively. Contact pads made of Ta (5 nm)/Cu (60 nm)/Pt (20 nm) are formed using optical lithography and liftoff. The effective magnetic anisotropy field (\(H_{\mathrm{K}}\)) is obtained via transport measurements. The Hall resistance is measured under the application of an in-plane magnetic field. The field at which the Hall resistance saturates is defined as \(H_{\mathrm{K}}\). Except for films with d less ~0.5 nm, we find the magnetic easy axis of the heterostructure points along with the film normal.

Machine learning

The convolutional neural network (CNN) system used in this paper contains twelve layers. The first ten are convolution and the remaining two are fully connected. The filter size of the convolution layers is 3 × 3, and the strides of the first six and the last four layers are 1 × 1 and 2 × 2, respectively. The number of the filters for each convolution layer is 64, 64, 40, 36, 32, 28, 24, 20, 16, and 16, respectively. The number of the units of the first fully connected layer is ten. The ReLU is applied to the output of all convolutions and the first fully connected layer. The Huber loss is used for loss calculation. The Adam algorithm is used for optimization. The network was trained using a commercial deep learning tool, Sony Neural Network Console, with a batch size of 64 for 100 epochs (https://dl.sony.com/app/).

The number of the testing images is fixed to 1/10 of the training images. For a given training data set, four machines are developed (since the order of the learning process is randomized, the results can be different even though the training data set used is the same). The material parameters estimated from the four machines are used to obtain the mean value and standard deviation. See Supplementary Figs. 2 and 3 for the details as well as the effect of cross-validation and data augmentation on the machine-learning performance. To estimate \(D\) from the experimental images (Fig. 4), we augment data with image rotation. Each image is rotated 90°, 180°, and 270° to generate three additional images. The four images are fed into the four machines to obtain 16 values of \(D\). The average value of the 16 data are shown in Fig. 4. The 95% confidence interval is calculated using the mean and the variance of the 16 data.

In addition to the convolutional neural network (CNN) system, we have tested a simple residual network (RN) network. See Supplementary Fig. 3 for the performance of the simple RN network.

Micromagnetic simulations

All micromagnetic simulations were performed using a GPU-based program developed previously40,41. The sample was divided into identical rectangular cells in which magnetization was assumed to be constant. The motion of magnetization was calculated by solving the Landau–Lifshitz–Gilbert equation with thermal noise42 (i.e., the Langevin equation).

$$\frac{{\partial \hat m}}{{\partial t}} = - \gamma \hat m \times \vec H_{{\mathrm{eff}}} + \alpha \hat m \times \frac{{\partial \hat m}}{{\partial t}}$$

Here, \(\gamma\), \(\hat m\), \(\vec H_{{\mathrm{eff}}}\), and \(\alpha\) are the gyromagnetic ratio, a unit vector representing the magnetization direction, the effective magnetic field, and the Gilbert damping constant. \(\vec H_{{\mathrm{eff}}}\) is calculated from the magnetic energy \(\varepsilon\):

$$\begin{array}{l}\vec H_{{\mathrm{eff}}} = - \frac{{\delta \varepsilon }}{{\delta \vec M}} + \vec h(t)\\\varepsilon = \varepsilon ^A + \varepsilon ^K + \varepsilon ^{DM} - \frac{1}{2}M_s\hat m \cdot \vec H^D\\\varepsilon ^A = A_{{\mathrm{ex}}}\left( {\nabla \hat m} \right)^2\\\varepsilon ^K = K_{\mathrm{u}}\left( {1 - m_z^2} \right)\\\varepsilon ^{DM} = D\left[ {\left( {m_x\frac{{\partial m_z}}{{\partial x}} - m_z\frac{{\partial m_x}}{{\partial x}}} \right) + \left( {m_y\frac{{\partial m_z}}{{\partial y}} - m_z\frac{{\partial m_y}}{{\partial y}}} \right)} \right]\\< h_i(t)h_j(t + \tau ) > = \frac{{2kT\alpha }}{{\left| \gamma \right|vM_s}}\delta (\tau )\delta _{ij}\end{array}$$

Here, \(\vec h\left( t \right)\) is the effective field associated with thermal energy, \(\varepsilon ^A\), \(\varepsilon ^K\), and \(\varepsilon ^{DM}\) are the exchange energy, the anisotropy energy and the DM interaction energy, and \(\vec H^D\) is the demagnetizing field. \(M_s\), \(A_{{\mathrm{ex}}}\), \(K_u\), \(D\), k, T, \(v\), \(\delta (\tau )\), and \(\delta _{ij}\) are the saturation magnetization, the exchange stiffness constant, the uniaxial magnetic anisotropy energy density, the DM exchange constant, the Boltzmann constant, temperature, the volume of the cell, the Dirac delta function, and the Kronecker delta, respectively. Note that \(K_{{\mathrm{eff}}} = K_{\mathrm{u}} - M_s^2/\left( {2\mu _0} \right).\) The demagnetizing field is calculated numerically.

We vary the pattern of anisotropy distribution and the initial magnetization configuration to generate images with different domain structures. These patterns (anisotropy distribution and the initial magnetization configuration) are created using random number generators. For the former (anisotropy distribution), square groups of 8 \(\times\) 8 cells were assigned a local anisotropy value randomly distributed according to a normal law with mean Ku and standard deviation \({\upsigma}\). For the latter (initial magnetization configuration), a random domain structure is created by uniform random numbers (−1 to 1) for each magnetization components (mx, my, mz) of each cell. Energy minimization is used to find the equilibrium state at T = 0 K (Fig. 2) or at T = 300 K (Fig. 4). \(\alpha\) is set to \(1.0\) to minimize computation time. Exemplary simulated images of the equilibrium state, with a fixed material parameter set, are shown in Supplementary Fig. 1. The materials parameters used in the calculations are summarized in Table 1.

The dimension of the cell is \(4 \times 4 \times t\,{\mathrm{nm}}^3\). t is the thickness of the ferromagnetic layer. The number of the cell is 512 × 512 (the image size is 2.048 × 2.048 μm2). The periodic boundary condition is employed to avoid effects from the edges. 110,000 simulations were carried out to produce the results presented in Fig. 2. To save computation time for machine learning, each image is converted to a 128 × 128 pixels image (one-pixel size is 16 × 16 nm2) using an averaging filter. Of the 110,000 images generated, 100,000 are used for training and the remaining 10,000 are used for validation (testing). For the results presented in Fig. 4, 27,500 simulations were performed and each image is rotated 90°, 180°, and 270° to obtain 110,000 images (see Supplementary Fig. 4 for the effect of data augmentation). Again, each image is converted to 128 × 128 pixels to match the pixel size of the image obtained in the experiments.