Introduction

Recently, many breakthroughs have been accomplished in preparing and measuring macroscopic and non-classical motional quantum states. These achievements enable many potential applications, such as ultra-sensitive measurements and quantum information processing taking advantage of acoustic modes. These mechanical systems also provide an ideal platform to investigate a pristine quantum system interacting with its environment.

Sideband cooling via interaction with an electromagnetic degree of freedom is a powerful technique to cool quantum systems, starting from small systems such as trapped ions1,2 or nanoparticles3,4,5,6, all the way up to nearly macroscopic mechanical resonators7,8,9,10,11,12,13,14,15,16,17,18,19. In the latter, ground-state cooling can be obtained relatively easily in a cavity optomechanics setup. Its implementation relies on coherently pumping the lower-frequency motional sideband of a cavity mode, promoting the coupling between motion and electromagnetic fields through the radiation pressure force. The interaction can be seen as reservoir engineering, where the oscillator is coupled to an effective cold bath, which mitigates and eventually dominates at large coupling rates the oscillator’s fluctuations coming from its hot intrinsic thermal bath. Related ideas are used to stabilize quantum squeezing20,21,22,23 and entanglement24,25 of mechanical oscillators. Engineered dissipation can then be used as a resource: state collapse upon measurements has been studied for usage in quantum computation26.

Here, we answer an even more intriguing question on dissipation and noise: can fluctuations, such as those arising from a hot bath, be used to prepare a mechanical system in a pure quantum state? Mari et al.27 have theoretically proposed to cool a mechanical oscillator in an optomechanical cavity by introducing the coupling to another, very hot, cavity mode. In their scheme, the hot mode establishes an interaction similar to that in sideband cooling between the oscillator and the cold cavity. Related studies have been presented28,29,30, including a connection to thermal machines31,32. In the present work, we realize the proposal of ref. 27, but in a manner recently discussed in ref. 33. Instead of using another cavity mode, we introduce noise at suitable frequency components of the same mode. Thereby, we investigate the relevance of the spectral content of the energy used in sideband-cooling experiments, conjecturing that cooling is obtained whether the driving power comes in the form of a coherent tone, or in the form of broadband noise.

Results

Theory

Let us consider a cavity optomechanical system. The mechanical oscillator of frequency ωm and damping rate γ is coupled to an environment at a temperature T, corresponding to the equilibrium thermal occupancy \({n}_{m}^{T}={\left[\exp (\hslash {\omega }_{m}/{k}_{B}T)-1\right]}^{-1}\). The oscillator’s position is denoted by x(t) = xzp(b† + b), with xzp the zero-point motion amplitude, and with the phonon creation and annihilation operators b†, b. The electromagnetic cavity has a frequency ωc and a damping rate κ, and is described by the photon operators a†, a. The oscillator is coupled parametrically to the cavity through the interaction Hc = ℏg0a†a(b† + b). Here, g0 is the single-photon radiation-pressure coupling in angular frequency units.

Let us first review the familiar sideband cooling with strong coherent drives, where the interaction can be linearized. In these protocols, the cavity is pumped with a single tone at a frequency close to the lower, “red” sideband, inducing a photon number n0 in the cavity. The linearized interaction becomes Hc = ℏG(a† + a)(b† + b), where the effective coupling is \(G={g}_{0}\sqrt{{n}_{0}}\). It is possible to show that the oscillator experiences an added optical damping equal to Γopt = 4G2/κ in the resolved-sideband limit ωm ≫ κ. As this additional damping is almost not accompanied by enhanced fluctuations, the oscillator is effectively cooled down to a thermal occupancy

$${n}_{m}=\frac{\gamma \,{n}_{m}^{T}+{\gamma }_{{{{{\rm{opt}}}}}}\,{n}_{ba}}{{\gamma }_{{{{{\rm{eff}}}}}}},$$
(1)

where the effective linewidth of the oscillator is γeff = γ + γopt, γopt is the added damping, and nba is a small correction due to a non-ideal sideband-resolution9,10—negligible in our experiment—or a classical occupation of the cavity mode. If sideband-cooling is the only process modifying the effective linewidth in the experiment, then γopt = Γopt.

The cooling due to radiation-pressure force can also be understood according to the description known as the quantum noise approach9,34,35,36,37. Let the oscillator be exposed to a force F(t), which will introduce an energy term HF(t) = − F(t)xzp(b† + b). The damping rate of the oscillator contributed by the force becomes \({\gamma }_{{{{{\rm{opt}}}}}}=\frac{{x}_{zp}^{2}}{{\hslash }^{2}}\left[{S}_{FF}({\omega }_{m})-{S}_{FF}(-{\omega }_{m})\right]\), where SFF(ω) is the spectral density of the force. Thus, the damping is given by the difference of the spectral densities at positive and negative frequencies. This is reminiscent of the absorption-emission asymmetry in quantum mechanics, however, the frequencies are now expressed in a rotating frame, and such an imbalance can also be constructed classically.

In the case of cavity optomechanics, the force is the radiation-pressure force \(F(t)=-\frac{\hslash {g}_{0}}{{x}_{zp}}{a}^{{{{\dagger}}} }a\). The damping is written \({\gamma }_{{{{{\rm{opt}}}}}}={g}_{0}^{2}\left[{S}_{\delta n\delta n}({\omega }_{m})-{S}_{\delta n\delta n}(-{\omega }_{m})\right]\) and can be interpreted as being due to fluctuations of the photon number n (Sδnδn(ωm) is the corresponding spectral density). The frequencies are here given with respect to ωc. Thus, if we can construct a photon number fluctuation spectrum very asymmetric with respect to the cavity frequency, significant cooling reminiscent of the sideband cooling is expected.

We now implement cooling by the noisy environment by introducing a fluctuating drive into the cavity. With a view to describing our experiment, the spectrum of this drive is modeled as a box function of width σ centered at the red sideband as shown in Fig. 1a. The spectrum is created by injecting band-filtered white electromagnetic noise into the cavity, corresponding to a flux of F0 photons per second, which gives rise to the time-averaged total photon number \({\bar{n}}_{0}\simeq \frac{\kappa {F}_{0}}{{\omega }_{m}^{2}}\) in the cavity. For details, see Methods. The damping becomes

$${\gamma }_{{{{{\rm{opt}}}}}}=\frac{4{g}_{0}^{2}{F}_{0}}{{\omega }_{m}^{2}}\frac{\kappa }{\sigma }{\tan }^{-1}\left(\frac{\sigma }{\kappa }\right),$$
(2)

and the phonon number is given by Eq. (1). For a given total photon flux, if the noise bandwidth is larger than κ, cooling will be moderately suppressed because most frequency components of the noise hit too far from the red sideband to induce efficient cooling. We note in passing that this effect is distinct from the halting of regular sideband cooling when G > κ/2 which is due to the fact that cavity cannot provide a proper dissipative bath, but the oscillator and cavity mode are coupled more strongly to each other than to their respective baths.

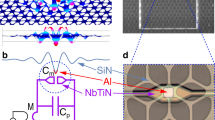
Fig. 1: Device and noise injection setup.
figure 1

a Band-limited microwave noise is created by upconverting MHz-frequency band-pass filtered noise up to the red mechanical sideband center frequency. b, c Electromechanical device, which supports a drumhead oscillator and two microwave cavity modes, which are used for the noise driving (frequency ωc), and for independent monitoring (frequency ωd) of the oscillator. Two cavity modes are defined by the combination of Al microstrip meander inductors and the moving drum capacitors.

Full size image

However, if the noise bandwidth is small, σ/κ ≪ 1, the analysis indicates that we recover the sideband-cooling result γopt ⇒ Γopt with \(G={g}_{0}\sqrt{{\bar{n}}_{0}}\), which would stay valid down to zero noise bandwidth. This seems to agree with the intuition that a given electromagnetic input flux applied in the same frequency range could power the same cooling. However, the issue is more complicated as will be discussed next.

Let us now examine in more detail what happens if the noise bandwidth is of the order of γeff or smaller. Now, the quantum-noise approach loses its validity, essentially because ensemble and time averages start to differ. In the intermediate regime γopt/σ ≈ 1, we can find perturbative corrections to the results from the quantum noise approach (see Methods). In the extreme limit γopt/σ ≫ 1, the oscillator’s damping adiabatically follows the slowly varying noise flux, giving a quasi-steady state at all times. We obtain that the cooling is, surprisingly, suppressed by a significant numerical factor in the latter limit. Physically, the reason is relatively simple: the occupation number is strongly dominated by instances of time when the cooling is weak, even though at other times the cooling is strong. Also, the profile of the time-averaged spectrum is very strongly dominated by periods of modest cooling associated to a narrow linewidth. In the limit γopt/σ ≫ 1, γopt/γ ≫ 1 the average phonon number and effective mechanical linewidth, as determined from the time-averaged spectrum, become

$${n}_{m}= \frac{\gamma {n}_{m}^{T}}{{\gamma }_{{{{{\rm{opt}}}}}}}\left[\ln \left(\frac{{\gamma }_{{{{{\rm{opt}}}}}}}{\gamma }\right)-C\right],\\ {\gamma }_{{{{{\rm{eff}}}}}}= \gamma \ln \left(\frac{{\gamma }_{{{{{\rm{opt}}}}}}}{\gamma }\right)\,.$$
(3)

Here, C is Euler’s constant.

Experimental setup

Our sample consists of a superconducting aluminum microcircuit which supports two microwave resonance modes (cavities), each coupled to two mechanical oscillators. The mechanical oscillators are drumhead membranes13,38 suspended above electrodes, forming displacement-dependent capacitors. For this experiment, we consider only one of the drums and ignore the other owing to a significant frequency separation. A schematic of the circuit design is shown in Fig. 1b. For more details, see Supplementary Note 2, and Supplementary Figs. 1 and 2.

The oscillator of interest is a 17 μm diameter aluminum drumhead resonating at ωm/2π ≃ 9.22 MHz with an intrinsic damping rate γi/2π ≃ 120 Hz. The cavity mode with the frequency ωc/2π ≃ 4.87 GHz is used as a “pump” cavity to implement cooling, as it has the larger electromechanical coupling g0/2π ≃ 39 Hz, allowing for stronger cooling effects. The higher-frequency, “probe” cavity with the corresponding parameters ωd/2π ≃ 6.42 GHz and g0,d/2π ≃ 34 Hz, is used for characterizing the oscillator thanks to calibrated thermometry. The coupling of the oscillator to the two cavities is schematically displayed in Fig. 1c. Both cavity modes satisfy the condition of resolved sideband limit where the respective damping rates of the pump and probe cavity κ/2π ≃ 1.06 MHz and κd/2π ≃ 0.84 MHz are much smaller than the mechanical frequency.

The device is studied at a temperature of  ~ 10 mK in a dilution refrigerator. We find that in the absence of active cooling and technical heating (see below), the mechanical mode is thermalized down to T ≃ 10.6 mK. Under these conditions, the thermal population is denoted by \({n}_{i,0}^{T}\), which we measure [Fig. S7(a)] as \({n}_{i,0}^{T}\simeq 24\).

Before describing the actual cooling-by-noise experiment, let us present the thermometry principle. We drive the probe cavity with a weak coherent tone at the red sideband, inducing the effective coupling Gd (Fig. 1c). This drops a thermal sideband at ωd reproducing the mechanical spectrum. However, one has to bear in mind that the probe causes dynamical backaction itself due to non-vanishing probe cooperativity \({{{{{\mathcal{C}}}}}}_{d}=\frac{4{G}_{d}^{2}}{{\kappa }_{d}{\gamma }_{i}}\). The associated residual sideband cooling creates an effective oscillator with the damping rate \(\gamma=(1+{{{{{\mathcal{C}}}}}}_{d}){\gamma }_{i}\) and the bath occupancy \({n}_{m}^{T}={n}_{i}^{T}{\gamma }_{i}/\gamma\). In the experiment, We select a probe power that is as small as possible but still allows for a detectable signal within hours of integration. This corresponds to a probe cooperativity \({{{{{\mathcal{C}}}}}}_{d}\simeq 2.2\) and a cooling by a factor of two of the oscillator by the probing, with γ/2π ≃ 260 Hz. The corresponding bath occupation \({n}_{m}^{T}\) depends on the microwave power due to technical heating. We include all this in the thermometry calibration carried out by regular sideband cooling analysis via the probe cavity, which allows to associate a mechanical occupancy to a spectral density of electromagnetic flux in the thermal sideband. In spite of cooling by the probe tone, the overall cooling will be fully dominated by the noise-induced cooling. For description of the thermometry calibration, see Supplementary Note 3.B. and Supplementary Fig. 7.

The noise with the tunable bandwidth σ is generated first in the MHz frequency range (see “Methods”). Digitally generated and -filtered pseudo-random numeric values are played at a rate of 100 MHz by an FPGA module to produce a voltage noise waveform with a box-function spectral profile centered at 7 MHz. This noise is then up-converted by mixing it with a local oscillator (LO) at ωc − ωm − 7 MHz. We thus obtain a sharply band-pass-filtered noise whose box-shaped spectrum is centered at the red sideband, with the original bandwidth σ. After additional analog filtering and processing, the noise injected is a good approximation to bandpass-filtered thermal noise.

Based on the room-temperature characterization of the injected noise, we cannot directly obtain a prediction for γopt, since F0 in Eq. (2) is difficult to determine experimentally at the sample, owing to the instrumental attenuation and noise separating the sample and the room-temperature equipment. We calibrate the product \({g}_{0}^{2}{F}_{0}\) using the sideband cooling effect of a standard coherent tone applied to the pump cavity, where we also utilize the ratio of total noise power versus the coherent tone power which we directly measure at room temperature (see Supplementary Note 3.A. and Supplementary Fig. 6).

Experimental results

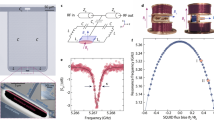
We now select a noise bandwidth σ/2π = 200 kHz, which is expected to yield a cooling close to optimum, and vary the integrated noise power. The effective damping shown in Fig. 2a follows closely the theoretical prediction which does not involve adjustable parameters. In Fig. 2b, we show ground-state cooling by noise, where we obtain mechanical occupancy nm ≃ 0.77 ± 0.08, integrated from the probe spectra as shown in Fig. 2c. The error bars indicate 95% statistical confidence bounds, similar to all other error bars presented in this study. The theoretical prediction in (b) describes a situation where the intrinsic baths of the mechanics and of the cavity retain their natural occupancies, that is, where the system does not suffer from “technical heating” induced by the applied microwave power. As seen, there are deviations from this model towards the largest noise flux, which is mostly attributed to heating of the mechanical bath, here up to \({n}_{i}^{T}\simeq 60\) quanta. Such heating, here quite modest, is typically observed in microwave-optomechanical experiments and remains unexplained thus far. Thanks to careful analog processing of the noise, we are confident that there is no significant noise leakage, i.e., heating by Sδnδn(−ωm) remains negligible.

Fig. 2: Ground-state cooling with noise.
figure 2

The noise bandwidth is kept constant at σ/2π = 200 kHz, while the incoming photon flux is varied. a The oscillator’s effective linewidth, and the theoretical prediction based on Eq. (2) expressed as a solid line. b Phonon number of the oscillator. The solid line presents Eq. (1), with \({n}_{m}^{T}\simeq 27\) slightly enhanced by probe’s technical heating. c Example probe spectra used for mode thermometry, at the photon numbers \({\bar{n}}_{0}=[24.1\times 1{0}^{3},2.43\times 1{0}^{5},1.53\times 1{0}^{6}]\) from top to bottom.

Full size image

Finally, in Fig. 3 we investigate how the cooling performance depends on the noise bandwidth, while the total noise flux is kept fixed. We vary the bandwidth over 4 decades, spanning from σ ≈ γ ≪ γopt up to σ > κ ≫ γopt. This way, we can examine the expected suppression of cooling in both extreme limits. The effective linewidth of the probe signal is shown first in Fig. 3a at different noise flux values. As discussed above, the low-bandwidth value is not of a strong physical significance but reflects that the spectrum is dominated by times with little cooling. The occupancy shown in Fig. 3b instead represents the time-averaged energy of the mechanical oscillator. The theory lines in Fig. 3 employ calibrated parameters, and a technical heating of \({n}_{m}^{T}\) for each \({\bar{n}}_{0}\) in Fig. 3b is the only adjustable parameter. The suppression of cooling in the large-bandwidth limit is well captured by the theory, however, there is a numerical discrepancy between the measured occupancy and the result of the theoretical model employed at low bandwidths. We believe this can be due to time-correlations in the repetitive noise signal introduced by our noise-generation method in a higher proportion for small-bandwidth noise.

Fig. 3: Noise bandwidth dependence of cooling.
figure 3

a Linewidth of the probe spectrum profile, and (b) Phonon occupancy, as functions of noise bandwidth. The photon numbers are \({\bar{n}}_{0}=1.57\times 1{0}^{6}\) (blue), \({\bar{n}}_{0}=7.9\times 1{0}^{5}\) (red), and \({\bar{n}}_{0}=2.0\times 1{0}^{5}\) (green). The solid lines are based on Eqs. (2) and (1). The dashed curves depict corrections to quantum noise approach when σ approaches γopt from above. Horizontal dashed lines depict low-bandwidth predictions, which are not shown for the lowest flux as Eq. (3) is not valid in this regime. The theoretical curves are color coded according to the experimental data.

Full size image

Discussion

In summary, we have cooled a mechanical oscillator close to its ground state by a noisy electromagnetic field. Our method could be extended to prepare not only the ground state but more sophisticated quantum states in mechanical systems relying on heat and fluctuations. If one would assign a temperature to the electromagnetic noise flux, the highest noise flux employed in the present experiment would be on the order of 108 Kelvins. Such a level of Johnson noise can clearly not be created by simply heating a resistor. However, g0 can be greatly enhanced in microwave optomechanical systems by introducing Josephson junctions or qubits that couple either capacitively39 or inductively40,41 to the mechanics. In ref. 39 as an example, values up to g0/2π ≈ 1 MHz have been reported at n0 ~ 1. At such a low photon number, where cooling is also possible42, we obtain that the temperature of the noisy environment that leads to ground-state cooling is in the Kelvin range (see Supplementary Note 3.C.). This environment can be created from ambient noise by cryogenic filtering and adjustable attenuation, and, intriguingly, one could use suitably filtered ambient noise for quantum state preparation.

Methods

Noise generation

Here, we describe and justify the schematics drawn in Fig. S4. The low-frequency noise is first created as a baseband noise signal with a box function spectral profile. The simplest option would be to create low-pass filtered noise using a simple RF function generator, spanning from zero frequency up to some cut-off, and then up-convert it with the Local Oscillator (LO). However, this would result in two correlated images of the baseband signal on either frequency side of the LO, possibly affecting the assumption of uncorrelated noise. For this reason, we decided to generate the baseband noise centered at a finite and relatively high frequency, here 7 MHz, with a sharp box-function spectral profile.

Standard function generators do not allow to generate such a specific spectrum. Furthermore, analog filtering of a low-pass filtered noise is not a suitable option, as standard analog filters do not provide steep enough roll-off. Therefore, we generate the noise signal using a sequence of 30 × 106 Gaussian-distributed random values from a random number generator (Ziggurat method, provided by the GSL library for C++). We then perform digital filtering on these points to create a box-shaped spectrum centered at 7 MHz. After scaling and formatting operations, these points are loaded into the Dynamic Random Access Memory (DRAM) associated to a FPGA processor (Kintex-7 325T, in a NI FlexRIO PXIe-7972 module) to be played with a 16-bit resolution (over a range of  ±2 V) at a sampling frequency of 100 MHz, by the output channel of a transceiver associated to the FPGA card. The number of points used in this method of noise generation is limited by the size of the DRAM available on the FPGA module. The noise trace that is fed to the DRAM lasts 0.3 s, and it is repeated in a loop. This timescale is much longer than any other timescale of the sample. However, these constraints impose a lower bound on the bandwidth of noise that can be reliably generated in this manner, as the number of frequency points participating in the bandwidth of noise becomes too low to establish a good statistics.

This noise is then mixed with the LO tone (ωLO = ωc − ωm − 7 MHz) to place the upper sideband of the mixing at the red optomechanical sideband of the pump cavity. The mixer employed here is a single-sideband (SSB) mixer, which efficiently suppresses the generation of the lower sideband as long as it sits further away than 4 MHz from the LO frequency. In the experiment, the signal in upper and lower sidebands extends over bandwidths of up to 4 MHz: the center of the lower sideband should therefore sit at least 6 MHz away from the LO so as to use the attenuation provided by the SSB mixer to suppress the whole bandwidth of the lower sideband. We chose an even larger LO detuning from the optomechanical sideband, of 7 MHz, so as to allow for further filtering of the lower sideband using an analog notch filter without affecting the upper sideband. The single-sideband mixer then rejects the undesired image of the noise below the LO frequency by about 25 dB, and we further notch-filter the image, since otherwise possibly detrimental intermodulation products will appear.

In the mixing operation, the LO signal leaks through the mixer, which results in a coherent signal at ωLO also propagating towards the sample. The optomechanical contribution of this coherent signal is not too strong since it is substantially detuned from the sideband and partially filtered by the notch filter used to suppress the lower sideband of the noise. However, we eliminate further it to make sure that the cooling is due to the noise alone. Therefore, this tone is actively canceled out by about 45 dB thanks to a destructive interference with a second tone of equal frequency generated by the same microwave generator (for phase stability), with an appropriate phase and amplitude. In all experiments, the power of the residual coherent tone is thus maintained at least 25 dB below the total integrated power of the noise.

The box-profiled microwave noise is then amplified by a 3 Watt power amplifier and sent through a notch filter at the pump cavity frequency, and through a 5 GHz low pass filter. The role of the notch filter is to eliminate harmful noise at the cavity frequency that would pose strong limits on available cooling. The low pass filter serves to mitigate broadband noise from the power amplifier being injected to the probe cavity, which can introduce extra heating to the mechanics, or interference in the probing. The relatively weak coherent probe tone is also going through a notch filter and a high pass filter, for the same reasons as described immediately above.

Examples of the generated noise spectra are shown in Fig. S5(a). We obtain sharp roll-off, about 9 dB per kHz even at the largest bandwidths.

The generated noise and coherent tone are combined with a power combiner and sent to the dilution refrigerator. Additionally, these two signals are split before the combiner to be sent through a separate line each containing a tunable amplitude attenuator and tunable phase shifter. As a result, the driving broadband noise and probe tone can be canceled inside the refrigerator after they are reflected from the sample before reaching the low-temperature HEMT amplifier. Without such canceling, we expect saturation of the HEMT or the last amplification stage at room temperature.

Noise calibration

Throughout all experiments, to compare the optomechanical impacts of noise and of coherent signals, we ensured that the total integrated power of the noise is equivalent to the power of the coherent tones employed, and this whatever the bandwidth of the noise. In practice, we calibrate the ratio of noise power to a coherent tone power at given generator settings (see Supplementary Note 3.A.). We realized calibration sweeps of the noise bandwidth and measured it after the whole signal conditioning chain as indicated by the calibration point marked in Fig. S3.

We found that the data stream from the FPGA already ensured that the power was constant within ± 0.2 dB at large bandwidths, but systematic variations up to 2.5 dB were seen at bandwidths < 500 Hz, which can be attributed to the small available statistics on the distribution of the noise within this technique. This was taken into account in rescaling of the noise amplitude, allowing to maintain the final integrated power constant within ± 0.5 dB. This bandwidth-dependent rescaling does not patch the lack of statistics, but at least allows the noise with its imperfect statistics to be used for comparison to other driving situations.

Finally, noise power sweeps were also performed at fixed bandwidths to ensure that none of the elements of the microwave setup (mixers, amplifiers) were saturated by the range of powers used in the experiments.

Model

We start from the quantum Langevin equations

$$\dot{a}=-\left(\frac{\kappa }{2}+i{\omega }_{c}\right)a-i{g}_{0}\left(b+{b}^{{{{\dagger}}} }\right)a+\sqrt{\kappa }\xi$$
(4)
$$\dot{b}=-\left(\frac{\gamma }{2}+i{\omega }_{m}\right)b-i{g}_{0}\left({a}^{{{{\dagger}}} }a-\langle {a}^{{{{\dagger}}} }a\rangle \right)+\sqrt{\gamma }\eta$$
(5)

where the Gaussian thermal noise from the mechanical bath is assumed to obey34

$$\langle {\eta }^{{{{\dagger}}} }[\omega ]\eta [{\omega }^{{\prime} }]\rangle={n}_{m}^{T}\,2\pi \delta (\omega+{\omega }^{{\prime} })$$
(6)
$$\langle \eta [\omega ]{\eta }^{{{{\dagger}}} }[{\omega }^{{\prime} }]\rangle=\left({n}_{m}^{T}+1\right)\,2\pi \delta (\omega+{\omega }^{{\prime} })$$
(7)

and \({n}_{m}^{T}\) is the bath’s thermal occupation number.

We also assume Gaussian input noise

$$\xi (t)={e}^{-i({\omega }_{c}-{\omega }_{m})t}\left({\xi }_{c}(t)+{\xi }_{q}(t)\right)$$
(8)

to the cavity mode, which we separate into a classical contribution ξc and a quantum operator ξq. The latter represents vacuum noise, such that \(\langle {\xi }_{q}^{{{{\dagger}}} }(t){\xi }_{q}({t}^{{\prime} })\rangle=0\). To satisfy standard commutation relations, the operator ξq must satisfy

$$\left[{\xi }_{q}[\omega ],{\xi }_{q}^{{{{\dagger}}} }[{\omega }^{{\prime} }]\right]=2\pi \delta (\omega+{\omega }^{{\prime} }),$$
(9)

where we define the Fourier transformation according to

$${f}^{({{{\dagger}}} )}[\omega ]=\int_{-\infty }^{\infty }dt\,{e}^{i\omega t}{f}^{({{{\dagger}}} )}(t).$$
(10)

Furthermore, we define

$$\langle {\xi }_{c}^{*}[\omega ]{\xi }_{c}[{\omega }^{{\prime} }]\rangle={N}_{{{{{\rm{in}}}}}}(-\omega )\,2\pi \delta (\omega+{\omega }^{{\prime} }),$$
(11)

such that the spectral content of the incoming noise is characterized by the function Nin. We will assume that the noise ξc has a spectrum centered around zero frequency, meaning that the incoming noise ξ is centered at the red sideband frequency

$${\omega }_{r}={\omega }_{c}-{\omega }_{m},$$
(12)

and we will denote the classical noise bandwidth by the symbol σ. The simplest function satisfying these properties is the rectangular function

$${N}_{{{{{\rm{in}}}}}}(\omega )=2\pi {N}_{0}\left\{\Theta [\omega+\sigma /2]-\Theta [\omega -\sigma /2]\right\},$$
(13)

which is constant in a frequency interval of width σ around zero frequency and vanishes otherwise. This is a good approximation to the noise spectrum produced in the experiments and is sufficient to explain the observed results both qualitatively and, to a large degree, quantitatively. We will assume that both the noise bandwidth and the cavity linewidth are much smaller than the mechanical resonance frequency, i.e.,

$$\kappa,\sigma \, \ll \, {\omega }_{m},$$
(14)

but we make no assumptions on the ratio σ/κ.

We will additionally assume that \(\langle \xi [\omega ]\xi [{\omega }^{{\prime} }]\rangle=0\), meaning that there are no correlations between the noise at different frequencies. Whether this is true depends on how the noise is actually generated. In any case, we do not expect that deviations from this will result in significant changes to the results from the quantum-noise approach below as long as the noise bandwidth is much smaller than the mechanical resonance frequency.

Quantum noise approach

In the weak-coupling regime γ, γopt ≪ κ, where the optomechanical damping rate γopt is to be defined, and for noise bandwidth σ ≫ γ, γopt, we can determine the mechanical oscillator’s average phonon number nm from the quantum noise approach34. We define the photon number fluctuation spectrum

$${S}_{\delta n\delta n}(\omega )=\int_{-\infty }^{\infty }d\tau \,{e}^{i\omega \tau }\langle \delta n(\tau )\delta n(0)\rangle,$$
(15)

with

$$\delta n={a}^{{{{\dagger}}} }a-\langle {a}^{{{{\dagger}}} }a\rangle .$$
(16)

In the quantum noise approach, the average phonon number is given by Marquardt et al., and Clerk et al.,9,34

$${n}_{m}=\frac{\gamma {n}_{m}^{T}+{\gamma }_{{{{{\rm{opt}}}}}}{n}_{ba}}{\gamma+{\gamma }_{{{{{\rm{opt}}}}}}}$$
(17)

with

$${\gamma }_{{{{{\rm{opt}}}}}}={g}_{0}^{2}\left({S}_{\delta n\delta n}^{(0)}({\omega }_{m})-{S}_{\delta n\delta n}^{(0)}(-{\omega }_{m})\right),$$
(18)
$${n}_{ba}=\frac{{S}_{\delta n\delta n}^{(0)}(-{\omega }_{m})}{{S}_{\delta n\delta n}^{(0)}({\omega }_{m})-{S}_{\delta n\delta n}^{(0)}(-{\omega }_{m})},$$
(19)

and where \({S}_{\delta n\delta n}^{(0)}(\omega )\) refers to the photon number fluctuation spectrum in absence of optomechanical coupling, i.e., for g0 = 0.

In the absence of optomechanical coupling, the cavity annihilation operator is

$${a}_{0}[\omega ]=\sqrt{\kappa }{\chi }_{c}(\omega -{\omega }_{r})\xi [\omega ],$$
(20)

with the cavity susceptibility defined as

$${\chi }_{c}(\omega )=\frac{1}{\kappa /2-i(\omega -{\omega }_{m})}.$$
(21)

Exploiting that the incoming noise is Gaussian, we can write

$${S}_{\delta n\delta n}^{(0)}(\omega )=\int_{-\infty }^{\infty }\frac{d{\omega }_{1}}{2\pi }\left[{S}_{{a}^{{{{\dagger}}} }a}^{(0)}({\omega }_{1}){S}_{a{a}^{{{{\dagger}}} }}^{(0)}(\omega -{\omega }_{1})+{S}_{{a}^{{{{\dagger}}} }{a}^{{{{\dagger}}} }}^{(0)}({\omega }_{1}){S}_{aa}^{(0)}(\omega -{\omega }_{1})\right]$$
(22)

where

$${S}_{AB}^{(0)}(\omega )=\int_{-\infty }^{\infty }\frac{d{\omega }^{{\prime} }}{2\pi }\langle {A}_{0}[\omega ]{B}_{0}[{\omega }^{{\prime} }]\rangle$$
(23)

and A and B are either a or a†.

Given the assumptions on the incoming noise ξ, we now find

$${S}_{\delta n\delta n}^{(0)}(\omega )= {\kappa }^{2}\int_{-\infty }^{\infty }\frac{d{\omega }_{1}}{2\pi }| {\chi }_{c}(-{\omega }_{1}){| }^{2}| {\chi }_{c}(\omega -{\omega }_{1}){| }^{2}\\ \times {N}_{{{{{\rm{in}}}}}}(-{\omega }_{1})\left[{N}_{{{{{\rm{in}}}}}}(\omega -{\omega }_{1})+1\right].$$
(24)

This can be straightforwardly determined from the input noise spectrum Nin(ω) and the cavity susceptibility χc(ω).

We now use the noise spectrum given by Eq. (13). We first note that, in the absence of optomechanical coupling, the average cavity photon number then becomes

$${\bar{n}}_{0}= \int_{-\infty }^{\infty }\frac{d\omega }{2\pi }{S}_{{a}^{{{{\dagger}}} }a}^{(0)}(\omega )=\kappa {N}_{0}\int_{-\sigma /2}^{\sigma /2}d\omega \,| {\chi }_{c}(\omega ){| }^{2} \\ \approx \frac{\kappa \sigma {N}_{0}}{{\omega }_{m}^{2}}=\frac{\kappa {F}_{0}}{{\omega }_{m}^{2}},$$
(25)

where

$${F}_{0}=\sigma {N}_{0}$$
(26)

is the total incoming photon flux.

We note that the product Nin(−ω1)Nin(ω − ω1) in Eq. (24), which describes stimulated emission of sideband photons, gives no contribution when ∣ω∣ > σ. Thus, for ω = ± ωm > σ, we get

$${S}_{\delta n\delta n}^{(0)}(\omega )= {\kappa }^{2}{N}_{0}\int_{-\sigma /2}^{\sigma /2}d{\omega }_{1}| {\chi }_{c}(-{\omega }_{1}){| }^{2}| {\chi }_{c}(\omega -{\omega }_{1}){| }^{2}\\ \approx \frac{{\kappa }^{2}{N}_{0}}{{\omega }_{m}^{2}}\int_{-\sigma /2}^{\sigma /2}d{\omega }_{1}| {\chi }_{c}(\omega -{\omega }_{1}){| }^{2}$$
(27)

in the limit (14). For ω = − ωm, this gives

$${S}_{\delta n\delta n}^{(0)}(-{\omega }_{m})\, \approx \, \frac{{\kappa }^{2}{F}_{0}}{4{\omega }_{m}^{4}},$$
(28)

whereas for ω = + ωm, we get

$${S}_{\delta n\delta n}^{(0)}({\omega }_{m})\, \approx \, \frac{2\pi \kappa {F}_{0}}{{\omega }_{m}^{2}\sigma }f\left(\frac{\sigma }{\kappa }\right),$$
(29)

when defining

$$f\left(\frac{\sigma }{\kappa }\right)=\frac{2}{\pi }\arctan \left(\frac{\sigma }{\kappa }\right).$$
(30)

We note that f(σ/κ) ≈ 1 for large bandwidths σ/κ ≫ 1, and that f(σ/κ) ≈ 2σ/(πκ) for small bandwidths σ/κ ≪ 1.

From Eq. (18), the optomechanical damping rate now becomes

$${\gamma }_{{{{{\rm{opt}}}}}}=\frac{{g}_{0}^{2}\kappa {F}_{0}}{{\omega }_{m}^{2}\sigma }\left[2\pi f\left(\frac{\sigma }{\kappa }\right)-\frac{\kappa \sigma }{{(2{\omega }_{m})}^{2}}\right]$$
(31)

For small bandwidths σ/κ ≪ 1 compared to the cavity linewidth, this becomes

$${\gamma }_{{{{{\rm{opt}}}}}}\, \approx \, \frac{4{g}_{0}^{2}{F}_{0}}{{\omega }_{m}^{2}}\, \approx \, \frac{4{G}^{2}}{\kappa }$$
(32)

with \(G={g}_{0}\sqrt{{\bar{n}}_{0}}\). This is just like the optomechanical damping rate familiar from coherent driving at the red sideband in the resolved sideband regime κ/ωm ≪ 1, where G is the enhanced optomechanical coupling proportional to the square root of the average cavity photon number. Conversely, for large bandwidths σ/κ ≫ 1, we find

$${\gamma }_{{{{{\rm{opt}}}}}} \, \approx \, \frac{2\pi {g}_{0}^{2}\kappa {F}_{0}}{{\omega }_{m}^{2}\sigma }\approx \frac{2\pi {G}^{2}}{\sigma }.$$
(33)

The above approximate expressions tell us that, for a constant input flux F0, the damping rate is constant in the small bandwidth regime σ/κ ≪ 1, but is reduced by a factor πκ/(2σ) in the large bandwidth regime σ/κ ≫ 1. The approximate damping rate is given by

$${\gamma }_{{{{{\rm{opt}}}}}} \, \approx \, \frac{4{g}_{0}^{2}{F}_{0}}{{\omega }_{m}^{2}}\cdot \frac{\pi \kappa }{2\sigma }f\left(\frac{\sigma }{\kappa }\right)$$
(34)

as a function of σ/κ for fixed input flux F0.

The quantum limit to the phonon number given by Eq. (19) becomes

$${n}_{ba} \approx \frac{{S}_{\delta n\delta n}^{(0)}(-{\omega }_{m})}{{S}_{\delta n\delta n}^{(0)}({\omega }_{m})}\\ \approx \frac{\kappa \sigma }{8\pi {\omega }_{m}^{2} \, f(\sigma /\kappa )}.$$
(35)

For small bandwidth σ/κ ≪ 1, this reduces to the limit \({n}_{ba}={(\kappa /4{\omega }_{m})}^{2}\) familiar from coherent driving9,10, whereas for large bandwidths σ/κ ≫ 1, it increases to \({n}_{ba}=\kappa \sigma /(8\pi {\omega }_{m}^{2})\), which is still much smaller than 1 with our assumptions.

Beyond the quantum noise approach

The quantum noise approach is no longer applicable when the noise bandwidth σ becomes so small as to be comparable to the effective mechanical linewidth γeff = γ + γopt. To address the low bandwidth regime, let us now go back to the equations of motion (4) and (5). Assuming that ξc(t) varies slowly on the timescale 1/κ, i.e., that the noise bandwidth σ is small compared to the cavity linewidth κ, we can write a linearized solution for the cavity field as

$$a(t) \, \approx \, {e}^{-i{\omega }_{r}t}\left[{a}_{0}(t)-i{g}_{0}\int_{-\infty }^{t}d\tau \,{e}^{-(\kappa /2+i{\omega }_{m})(t-\tau )}\left(b(\tau )+{b}^{{{{\dagger}}} }(\tau )\right){a}_{0}(\tau )\right],$$
(36)

where

$${a}_{0}(t) \, \approx \, \frac{\sqrt{\kappa }{\xi }_{c}(t)}{\kappa /2+i{\omega }_{m}}+{\zeta }_{q}(t)$$
(37)

is the approximate solution, in a frame rotating at ωr, in absence of optomechanical coupling and where

$${\zeta }_{q}(t)=\int_{-\infty }^{t}d\tau \,{e}^{-(\kappa /2+i{\omega }_{m})(t-\tau )}\,\sqrt{\kappa }\,{\xi }_{q}(\tau ).$$
(38)

The equation of motion for the phonon annihilation operator is then approximately given by

$$\dot{b} \, \approx -\left(\frac{\gamma }{2}+i{\omega }_{m}\right)b-\frac{2{g}_{0}^{2}}{{\omega }_{m}^{2}}{\xi }_{c}^{*}(t){\xi }_{c}(t)\,b\\ +\sqrt{\gamma }\eta -i{g}_{0}\left(\frac{\sqrt{\kappa }{\xi }_{c}^{*}(t)}{\kappa /2-i{\omega }_{m}}{\zeta }_{q}(t)+\frac{\sqrt{\kappa }{\xi }_{c}(t)}{\kappa /2+i{\omega }_{m}}{\zeta }_{q}^{{{{\dagger}}} }(t)\right)\\ -i{g}_{0}\frac{\kappa }{{\omega }_{m}^{2}}\left[{\xi }_{c}^{*}(t){\xi }_{c}(t)-\langle {\xi }_{c}^{*}(t){\xi }_{c}(t)\rangle \right].$$
(39)

when we assume the resolved sideband regime κ ≪ ωm. It is worth noting that only the classical amplitude noise ∣ξc∣ enters here, not the classical phase noise, which is a consequence of assuming a noise bandwidth σ ≪ κ.

The last term in the first line of Eq. (39) describes optical damping of the mechanical mode. In the limit where the autocorrelation time of the noise ξc(t) is much shorter than the effective mechanical lifetime, we can approximate \({\xi }_{c}^{*}(t){\xi }_{c}(t)=| {\xi }_{c}(t){| }^{2}\) by its average value here. However, this is not appropriate when the noise bandwidth is small enough to be comparable with the mechanical damping rate.

The second line of Eq. (39) describes both thermal noise and radiation pressure shot noise that can drive the mechanical resonator at its resonance frequency. The last line, however, describes low-frequency noise, i.e., slow variations in the radiation pressure force experienced by the mechanical oscillator, which leads to slow variations in its equilibrium position and thereby variations in the cavity resonance frequency. However, as long as these frequency variations are sufficiently small compared to the cavity linewidth, we can ignore the last line.

Since ξc(t) is classical noise, i.e., commutes with itself at different times, the solution of Eq. (39) becomes

$$b(t)=\int_{-\infty }^{t}d\tau \,{e}^{-(\gamma /2+i{\omega }_{m})(t-\tau )-\Gamma (t,\tau )/2}\Lambda (\tau )$$
(40)

when defining

$$\Gamma (t,\tau )=\frac{4{g}_{0}^{2}}{{\omega }_{m}^{2}}\int_{\tau }^{t}ds\,{\xi }_{c}^{*}(s){\xi }_{c}(s)$$
(41)

and

$$\Lambda (t)=\sqrt{\gamma }\eta (t)-i{g}_{0}\left(\frac{\sqrt{\kappa }{\xi }_{c}^{*}(t)}{\kappa /2-i{\omega }_{m}}{\zeta }_{q}(t)+\frac{\sqrt{\kappa }{\xi }_{c}(t)}{\kappa /2+i{\omega }_{m}}{\zeta }_{q}^{{{{\dagger}}} }(t)\right).$$
(42)

In the following, we will ignore the last term in Λ(t) for simplicity, meaning that we ignore radiation pressure shot noise. This is a good approximation in the resolved sideband regime κ ≪ ωm.

The ensemble averaged phonon number now becomes

$${n}_{m}=\langle {b}^{{{{\dagger}}} }(t)b(t)\rangle \, \approx \, \gamma {n}_{m}^{T}\int_{-\infty }^{t}d\tau \,{e}^{-\gamma (t-\tau )}\left\langle {e}^{-\Gamma (t,\tau )}\right\rangle .$$
(43)

We also define the mechanical spectral density as

$${S}_{{b}^{{{{\dagger}}} }b}(\omega )= \int_{-\infty }^{\infty }d\tau \,{e}^{i\omega \tau }\langle {b}^{{{{\dagger}}} }(t+\tau )b(t)\rangle \\ \approx \gamma {n}_{m}^{T}\int_{-\infty }^{\infty }d\tau \,{e}^{i(\omega+{\omega }_{m})\tau }\\ \times \int_{-\infty }^{\min (t,t+\tau )}d{\tau }_{1}\,{e}^{-\gamma (t+\tau /2-{\tau }_{1})}\left\langle {e}^{-\left[\Gamma (t+\tau,{\tau }_{1})+\Gamma (t,{\tau }_{1})\right]/2}\right\rangle .$$
(44)

To evaluate the integrals in these expressions, we will need the relations

$$\langle {\xi }_{c}^{*}(t){\xi }_{c}({t}^{{\prime} })\rangle=\int_{-\infty }^{\infty }\frac{d\omega }{2\pi }{e}^{-i\omega (t-{t}^{{\prime} })}{N}_{{{{{\rm{in}}}}}}(-\omega )$$
(45)

and

$$\langle {\xi }_{c}^{*}(t){\xi }_{c}(t)\rangle=\int_{-\infty }^{\infty }\frac{d\omega }{2\pi }{N}_{{{{{\rm{in}}}}}}(-\omega )=\sigma {N}_{0}={F}_{0}$$
(46)

where F0 is the average incoming photon flux as defined in Eq. (26).

Beyond the quantum noise approach, large bandwidth limit σ ≫ γ, γ opt

We will start by considering the large bandwidth limit where the noise bandwidth σ is large compared to the optical damping rate γopt of the mechanical oscillator. This will allow us to derive approximate expressions for the average phonon number nm and the effective mechanical linewidth γeff to first order in γopt/σ.

To find an expression for the average phonon number, we start by defining

$${\gamma }_{{{{{\rm{opt}}}}}}=\frac{4{g}_{0}^{2}{F}_{0}}{{\omega }_{m}^{2}},$$
(47)

which is the approximate optomechanical damping rate in the large bandwidth limit σ ≫ γopt (see Eq. (32)). We may then write

$$\Gamma (t,\tau )={\gamma }_{{{{{\rm{opt}}}}}}(t-\tau )+\frac{{\gamma }_{{{{{\rm{opt}}}}}}}{{F}_{0}}\int_{\tau }^{t}ds\left({\xi }_{c}^{*}(s){\xi }_{c}(s)-{F}_{0}\right).$$
(48)

We now expand the exponent in Eq. (43) to second order in the second term of Eq. (48), which, as we will see, is equivalent to expanding in γopt/σ. This gives

$$\left\langle {e}^{-\Gamma (t,\tau )}\right\rangle= {e}^{-{\gamma }_{{{{{\rm{opt}}}}}}(t-\tau )}\left[1+\frac{1}{2}{\left(\frac{{\gamma }_{{{{{\rm{opt}}}}}}}{{F}_{0}}\right)}^{2}\int_{\tau }^{t}d{s}_{1}\int_{\tau }^{t}d{s}_{2}\right.\\ \times \left.\left\langle \left({\xi }_{c}^{*}({s}_{1}){\xi }_{c}({s}_{1})-{F}_{0}\right)\left({\xi }_{c}^{*}({s}_{2}){\xi }_{c}({s}_{2})-{F}_{0}\right)\right\rangle \right]\\ = {e}^{-{\gamma }_{{{{{\rm{opt}}}}}}(t-\tau )}\left[1+\frac{1}{2}{\left(\frac{{\gamma }_{{{{{\rm{opt}}}}}}}{{F}_{0}}\right)}^{2}\times \int_{\tau }^{t}d{s}_{1}\int_{\tau }^{t}d{s}_{2}\left\langle {\xi }_{c}^{*}({s}_{1}){\xi }_{c}({s}_{2})\right\rangle \left\langle {\xi }_{c}({s}_{1}){\xi }_{c}^{*}({s}_{2})\right\rangle \right]\\= {e}^{-{\gamma }_{{{{{\rm{opt}}}}}}(t-\tau )}\left[1+\frac{1}{2}{\left(\frac{{\gamma }_{{{{{\rm{opt}}}}}}}{{F}_{0}}\right)}^{2}\int_{-\infty }^{\infty }\frac{d\omega }{2\pi }\int_{-\infty }^{\infty }\frac{d{\omega }^{{\prime} }}{2\pi }\right.\\ \times \left.\frac{{\sin }^{2}\left[(\omega+{\omega }^{{\prime} })(t-\tau )/2\right]}{{[(\omega+{\omega }^{{\prime} })/2]}^{2}}{N}_{{{{{\rm{in}}}}}}(-\omega ){N}_{{{{{\rm{in}}}}}}({\omega }^{{\prime} })\right]$$
(49)

when using Wick’s theorem. For small γopt/σ, we can simplify the frequency integrals by the approximation

$$\frac{{\sin }^{2}\left[(\omega+{\omega }^{{\prime} })(t-\tau )/2\right]}{{[(\omega+{\omega }^{{\prime} })/2]}^{2}}\to 2\pi (t-\tau )\delta (\omega+{\omega }^{{\prime} }),$$
(50)

such that

$$ \int \frac{d\omega }{2\pi }\int\frac{d{\omega }^{{\prime} }}{2\pi }\frac{{\sin }^{2}\left[(\omega+{\omega }^{{\prime} })(t-\tau )/2\right]}{{[(\omega+{\omega }^{{\prime} })/2]}^{2}}{N}_{{{{{\rm{in}}}}}}(-\omega ){N}_{{{{{\rm{in}}}}}}({\omega }^{{\prime} })\\ \approx \, (t-\tau )\int\frac{d\omega }{2\pi }{N}_{{{{{\rm{in}}}}}}^{2}(-\omega )=2\pi {N}_{0}^{2}\sigma (t-\tau ).$$
(51)

Inserting this in Eq. (49) gives

$$\left\langle {e}^{-\Gamma (t,\tau )}\right\rangle={e}^{-{\gamma }_{{{{{\rm{opt}}}}}}(t-\tau )}\left[1+\pi \frac{{\gamma }_{{{{{\rm{opt}}}}}}^{2}(t-\tau )}{\sigma }\right]$$
(52)

Using

$$\int_{-\infty }^{t}d\tau \,{e}^{-(\gamma+{\gamma }_{{{{{\rm{opt}}}}}})(t-\tau )}=\frac{1}{\gamma+{\gamma }_{{{{{\rm{opt}}}}}}}$$
(53)
$$\int_{-\infty }^{t}d\tau \,(t-\tau ){e}^{-(\gamma+{\gamma }_{{{{{\rm{opt}}}}}})(t-\tau )}=\frac{1}{{\left(\gamma+{\gamma }_{{{{{\rm{opt}}}}}}\right)}^{2}},$$
(54)

the phonon number (43) then becomes

$${n}_{m} \approx \frac{\gamma {n}_{m}^{T}}{\gamma+{\gamma }_{{{{{\rm{opt}}}}}}}\left(1+\frac{\pi {\gamma }_{{{{{\rm{opt}}}}}}^{2}}{(\gamma+{\gamma }_{{{{{\rm{opt}}}}}})\sigma }\right)\\= {n}_{m}^{{{{{\rm{(QNA)}}}}}}\left(1+\frac{\pi {\gamma }_{{{{{\rm{opt}}}}}}^{2}}{(\gamma+{\gamma }_{{{{{\rm{opt}}}}}})\sigma }\right).$$
(55)

Here, \({n}_{m}^{{{{{\rm{(QNA)}}}}}}\) is the result one finds from the quantum noise approach when σ ≪ κ ≪ ωm. The second term in the paranthesis is the correction as σ starts to approach γopt from above.

Expanding in the fluctuations, i.e., the second term of Eq. (48) as before, and using the same approximation (50), gives the spectral density

$$S(\omega )= \gamma {n}_{m}^{T}\int_{-\infty }^{\infty }d\tau \,{e}^{i(\omega+{\omega }_{m})\tau }\\ \times \int_{-\infty }^{\min (t,t+\tau )}ds\,{e}^{-(\gamma+{\gamma }_{{{{{\rm{opt}}}}}})(t+\tau /2-s)}\left[1+\frac{\pi {\gamma }_{{{{{\rm{opt}}}}}}^{2}}{\sigma }\left(t+\frac{\tau }{2}-s\right)\right].$$
(56)

To lowest order in γopt/σ, the s-integral gives

$$S(\omega )={n}_{m}\int_{-\infty }^{\infty }d\tau \,{e}^{i(\omega+{\omega }_{m})\tau }{e}^{-{\gamma }_{{{{{\rm{eff}}}}}}| \tau | /2}$$
(57)

with nm as in Eq. (55) and when defining the effective mechanical damping rate

$${\gamma }_{{{{{\rm{eff}}}}}}=\gamma+{\gamma }_{{{{{\rm{opt}}}}}}\left(1-\frac{\pi {\gamma }_{{{{{\rm{opt}}}}}}}{\sigma }\right).$$
(58)

Finally, evaluating the τ-integral gives the Lorentzian spectrum

$$S(\omega )=\frac{{\gamma }_{{{{{\rm{eff}}}}}}{n}_{m}}{{({\gamma }_{{{{{\rm{eff}}}}}}/2)}^{2}+{(\omega+{\omega }_{m})}^{2}}.$$
(59)

Beyond the quantum noise approach, small bandwidth limit σ ≪ γ, γ opt

In the regime where the noise bandwidth σ is the smallest rate in the problem, we can approximate (41) by

$$\Gamma (t,\tau )\, \approx \, \frac{4{g}_{0}^{2}{\xi }_{c}^{*}(t){\xi }_{c}(t)}{{\omega }_{m}^{2}}(t-\tau ),$$
(60)

which means that the mechanical damping follows the amplitude noise adiabatically in this regime.

We are now considering the case where the mechanical mode reaches a quasi-steady state on a time scale much faster than the scale at which the noise amplitude

$$r(t)=| {\xi }_{c}(t)|$$
(61)

varies. It is then useful to think about a time-dependent average phonon number, which we write

$${\langle {b}^{{{{\dagger}}} }(t)b(t)\rangle }_{r(t)}=\frac{\gamma {n}_{m}^{T}}{\gamma+4{g}_{0}^{2}{r}^{2}(t)/{\omega }_{m}^{2}}.$$
(62)

This expression comes about by performing the τ-integral in Eq. (43) while treating r2(t) as a constant, which is appropriate if the noise bandwidth σ is much smaller than the thermal equilibration rate of the oscillator. As before, in order to simplify, we ignore the second term in the numerator, i.e., the heating term due to radiation pressure shot noise. We can interpret (62) as a time-dependent average phonon number, where the time dependence comes from the particular realization of the noise ξc(t). Clearly, for times when ∣ξc(t)∣ is small, this becomes large, and vice versa.

If we now ensemble average \({\langle {b}^{{{{\dagger}}} }(t)b(t)\rangle }_{r(t)}\) over the noise ξc(t), the realizations where r(t) is small will contribute the most, such that the full ensemble average (or long time average) should become larger than the result \({n}_{m}^{{{{{\rm{(QNA)}}}}}}\) from the quantum noise approach, since 〈1/(c + dr2)〉 > 1/(c + d〈r2〉), but still smaller than \({n}_{m}^{T}\).

We assume that the classical and complex ξc(t) is drawn from a Gaussian probability distribution with zero mean, i.e., it is distributed according to

$$\tilde{P}({\xi }_{c})=\frac{1}{{{{{\mathcal{N}}}}}}{e}^{-k| {\xi }_{c}{| }^{2}},$$
(63)

where k is a constant to be determined and \({{{{\mathcal{N}}}}}\) is a normalization constant. Transforming to polar coordinates and integrating over the polar angle gives the probability distribution over amplitudes r = ∣ξc∣:

$$P(r)=r\int_{0}^{2\pi }d\varphi \,\tilde{P}(r{e}^{i\varphi })=\frac{2\pi }{{{{{\mathcal{N}}}}}}r{e}^{-k{r}^{2}},$$
(64)

where the additional factor of r comes from the Jacobian determinant. We note that, even though ξc has zero mean, i.e., there is no phase coherence of the incoming noise, the amplitude r > 0 does not have zero mean and does not obey Gaussian statistics.

Let us first determine the normalization constant \({{{{\mathcal{N}}}}}\) by requiring

$$\int_{0}^{\infty }dr\,P(r)=1,$$
(65)

giving

$${{{{\mathcal{N}}}}}=\frac{\pi }{k}$$
(66)

such that

$$P(r)=2kr{e}^{-k{r}^{2}}.$$
(67)

We can now determine the constant k from Eq. (46), i.e., by requiring that

$$\langle {r}^{2}\rangle=\int_{0}^{\infty }dr\,{r}^{2}P(r)={F}_{0}.$$
(68)

This gives

$$k=\frac{1}{{F}_{0}},$$
(69)

i.e., the width of the Gaussian (63) is given by the incoming flux F0.

Let us now calculate the phonon number nm averaged over different realizations of the incoming noise, i.e., the average of Eq. (62). We can then express the phonon number as

$${n}_{m}={n}_{m}^{T}\tilde{I}(k,\, q),$$
(70)

where we have defined the integral

$$\tilde{I}(k,\, q)=\int_{0}^{\infty }dr\,\frac{1}{1+q{r}^{2}}P(r)=2k\int_{0}^{\infty }dr\,\frac{r{e}^{-k{r}^{2}}}{1+q{r}^{2}}$$
(71)

and the constant

$$q=\frac{4{g}_{0}^{2}}{\gamma {\omega }_{m}^{2}}.$$
(72)

By a change of variables u = qr2, we can transform the integral to

$$\tilde{I}(k,\, q)=\lambda \int_{0}^{\infty }du\,\frac{{e}^{-\lambda u}}{1+u}\equiv I(\lambda )$$
(73)

when defining

$$\lambda=\frac{k}{q}=\frac{\gamma }{{\gamma }_{{{{{\rm{opt}}}}}}},$$
(74)

where γopt, defined as in Eq. (47), is the optomechanical damping one would have with coherent driving with flux F0, as before.

To our knowledge, it is not possible to find an analytical expression for the integral I(λ) in (73), although it is possible to express it as

$$I(\lambda )=\lambda\, {e}\, ^{\lambda }\,\Gamma (0,\, \lambda ),$$
(75)

where

$$\Gamma (s,\, x)=\int_{x}^{\infty }{t}^{s-1}{e}^{-t}$$
(76)

is the upper incomplete gamma function. However, we may proceed by considering the (most interesting) regime

$$\lambda \, \ll \, 1,$$
(77)

i.e., what would correspond to the damping being dominated by the optomechanical interaction in the case of coherent driving. We start by rewriting the integral as

$$I(\lambda )={\lambda }^{2}\int_{0}^{\infty }du\,\ln (1+u){e}^{-\lambda u}$$
(78)

which follows from partial integration. We now assume that the integral is dominated by large values u ≫ 1 for λ ≪ 1. We may then approximate the integrand such that

$$I(\lambda ) \, \approx \, {\lambda }^{2}\int_{0}^{\infty }du\,\ln u\,{e}^{-\lambda u}\\= \lambda \int_{0}^{\infty }dx\,\left(\ln x-\ln \lambda \right){e}^{-x}.$$
(79)

By introducing Euler’s constant

$$C=-\int_{0}^{\infty }dx\,\ln x\,{e}^{-x}=0.5775772156649...,$$
(80)

we now find

$$I(\lambda )\, \approx \, \lambda \left(\ln {\lambda }^{-1}-C\right).$$
(81)

By inserting Eq. (81) into Eq. (70), we then arrive at an analytical expression for the phonon number in the limit where the noise bandwidth is much smaller than the thermal equilibration rate:

$${n}_{m}=\frac{\gamma {n}_{m}^{T}}{{\gamma }_{{{{{\rm{opt}}}}}}}\left[\ln \left(\frac{{\gamma }_{{{{{\rm{opt}}}}}}}{\gamma }\right)-C\right].$$
(82)

We observe that this satisfies

$$\frac{\gamma {n}_{m}^{T}}{{\gamma }_{{{{{\rm{opt}}}}}}} \, < \, {n}_{m} < {n}_{m}^{T},$$
(83)

i.e., its value lies between the wide bandwidth (or coherent driving) phonon number and the thermal bath occupation number, as expected.

Let us now define the mechanical spectrum for a particular fixed value of the noise amplitude r as

$${S}_{r}(\omega )= \int_{-\infty }^{\infty }d\tau \,{e}^{i\omega \tau }{\langle {b}^{{{{\dagger}}} }(t+\tau )b(t)\rangle }_{r}\\= \frac{\gamma {n}_{m}^{T}}{{\left[(\gamma+{\gamma }_{{{{{\rm{opt}}}}}}{r}^{2}/{F}_{0})/2\right]}^{2}+{(\omega+{\omega }_{m})}^{2}}$$
(84)

where we, as in the previous section, ignore the radiation pressure shot noise term for simplicity. For noise bandwidths smaller than the thermalization rate, the actual spectrum one would measure for sampling times much longer than the noise correlation time is

$$S(\omega )=\int_{0}^{\infty }dr\,{S}_{r}(\omega )P(r).$$
(85)

We first note that the area under the spectrum gives the average phonon number, since

$$\int_{-\infty }^{\infty }\frac{d\omega }{2\pi }S(\omega )=\int_{0}^{\infty }drP(r)\int_{-\infty }^{\infty }\frac{d\omega }{2\pi }{S}_{r}(\omega )\\={n}_{m}^{T}I(\lambda )={n}_{m}.$$
(86)

Finding the explicit form of the average spectrum (85) is not straightforward. However, let us attempt to fit it to a Lorentzian, i.e., let’s write S(ω) ≈ L(ω) with

$$L(\omega )=\frac{{\gamma }_{{{{{\rm{eff}}}}}}{n}_{m}}{{({\gamma }_{{{{{\rm{eff}}}}}}/2)}^{2}+{(\omega+{\omega }_{m})}^{2}}.$$
(87)

It is straightforward to check that Eq. (86) is satisfied in this approximation. We now fit the Lorentzian by defining the effective linewidth γeff such that the height of the Lorentzian matches the actual maximum of the spectrum, i.e., we demand

$$L(-{\omega }_{m})=S(-{\omega }_{m}).$$
(88)

This means that

$$\frac{4{n}_{m}}{{\gamma }_{{{{{\rm{eff}}}}}}}= \int_{0}^{\infty }dr\,{S}_{r}(-{\omega }_{m})P(r)\\= \frac{4{n}_{m}^{T}}{\gamma }\lambda \int_{0}^{\infty }du\,\frac{{e}^{-\lambda u}}{{(1+u)}^{2}}$$
(89)

where λ is defined as before in Eq. (74). Partial integration then gives

$$\frac{4{n}_{m}}{{\gamma }_{{{{{\rm{eff}}}}}}} \,= \frac{4{n}_{m}^{T}}{\gamma }\lambda \left[1-\lambda \int_{0}^{\infty }du\,\frac{{e}^{-\lambda u}}{1+u}\right]\\= \frac{4\left({n}_{m}^{T}-{n}_{m}\right)}{{\gamma }_{{{{{\rm{opt}}}}}}},$$
(90)

such that

$${\gamma }_{{{{{\rm{eff}}}}}}={\gamma }_{{{{{\rm{opt}}}}}}\frac{{n}_{m}}{{n}_{m}^{T}-{n}_{m}}.$$
(91)

For \({n}_{m}\, \ll \, {n}_{m}^{T}\), this becomes

$${\gamma }_{{{{{\rm{eff}}}}}}=\gamma \ln \left(\frac{{\gamma }_{{{{{\rm{opt}}}}}}}{\gamma }\right).$$
(92)

Relation to strong-coupling limit, G > κ/2

In a traditional optomechanical situation (call it now case A) with coherent pumping at the red sideband, sideband cooling is halted in the strong-coupling limit, G > κ/2. In this case, the bandwidth of the electromagnetic reservoir given by κ roughly equals Γopt. Therefore, one may wonder if this is the same or at least analogous phenomenon to our current situation (say, case B) where cooling is halted when the noise bandwidth is on the same order of γopt. However, the similarity is only superficial.

Cases A and B differ in terms of the correlation time of the bath, i.e., if the reservoir seen by the mechanics is Markovian or not.

In case A the oscillator and cavity mode are coupled more strongly to each other than to their respective baths. When G is increased in regular sideband cooling such that one approaches case A, the coherent exchange coupling between mechanics and electromagnetics starts to dominate: one usually looks at this in terms of normal-mode splitting, but this can also be treated such that the electromagnetic cavity acts as a non-Markovian bath that returns back the mechanical excitations previously absorbed.

Case B entails weak-coupling description, given that the cavity is assumed to be unperturbed by the mechanics. The cavity just acts as a “bus” between mechanics and the electromagnetic reservoir. In case B, the “noise" experienced by the mechanics does not have a very low bandwidth even in our limit σ < γopt. For κ ≫ γopt, the cavity still acts as a Markovian bath for the oscillator, i.e., the oscillator still experiences (approximately) white noise from coupling to the cavity. It is the autocorrelation time of the slowly varying input field ξ(t) (or, consequently, that of the photon number) that becomes large, not the correlation time of the dissipative bath. The quantum noise approach thus gives the right instantaneous decay rate, but it does not give the right time-averaged properties.