Introduction

Electrons in 1D quantum systems exhibit striking phenomena, including the breakdown of Fermi liquid theory and quasiparticle formation in favor of collective modes1. Likewise, electrons confined to two dimensions and subjected to perpendicular magnetic fields exhibit the quantum Hall effects (QHEs)2. Although the microscopic details of QHE states are still an active area of research3,4, their low-energy transport properties are known to be governed by chiral, 1D edge channels5,6,7,8. These edge channels (ECs) conduct charge ballistically, allowing for phase-coherent electronic experiments9,10. In particular, electronic Fabry-Pérot (FP) QHE interferometry11,12,13, was performed extensively in GaAs, culminating in the observation of interference phase jumps as evidence for anyonic statistics of fractional quasiparticles14,15,16,17. Recently, FPs were developed in graphene, which showed Aharonov-Bohm (AB) interference of integer ECs18,19,20, with oscillation periodicity set by the magnetic flux quantum for electrons \({\Phi }_{0}\equiv h/e\). Our previous design18 utilized graphite gates encapsulating the graphene channel, which screened bulk charges. Without such screening layers21, however, interferometers exhibit ‘Coulomb dominated’ (CD) behavior in which strong coupling of the interfering EC to localized compressible states in the bulk determines the oscillation periodicity and obscures the expected AB oscillations13,22,23,24.

When bulk charges were strongly screened, GaAs FPs showed unexpected doubling of the AB oscillation frequency and shot noise corresponding to charge \(2e\) when interfering the outermost EC with the bulk of the interferometer in filling \(2.5 \, \le \, \nu \, \le \, 4.5\), suggesting a possibility of ‘pairing’ of elementary charges25. Furthermore, the coherence and periodicity of the interfering outer EC were related to the coherence and the enclosed flux of the adjacent inner EC26, and the ‘pairing’ phenomena only occurred when the outer two modes belonged to the same spin-split Landau level27. Independently, single-electron capacitance measurements in GaAs quantum dots revealed that tunneling into the edge of the dot corresponded to the entrance of two electrons rather than one for \(\nu \ge 2\), and that near \(\nu \, \approx \, 2.5\) the charging peaks follow doubled magnetic flux frequency28. Mechanisms of electron pairing are important questions in emergent phenomena, e.g. high-temperature superconductivity29 and the even-denominator fractional QHE states in GaAs30 and bilayer graphene31,32. However, theoretical work concerning FP interferometers was able to explain the doubled AB oscillation frequency based on a microscopic model without explicit introduction of electron pairing, though explaining other related phenomena in GaAs remains challenging33.

In this work, we experimentally address the microscopic mechanism of coupling between QHE edges by elucidating the relation between AB oscillation phase jumps and frequency doubling, employing a highly tunable QHE FP interferometer with strongly screened bulk charge in graphene. We observe periodically modulating interference phase jumps on the outer EC leading to nearly doubled AB oscillation frequency as we increase the electron density in-situ, unveiling a density-induced transition which was not explored in GaAs. We find that strong repulsive interactions between the outermost pair of spin-split ECs can explain both the observation of interference phase jumps and the approximately doubled interference frequency.

Results

Interferometer design and tuning

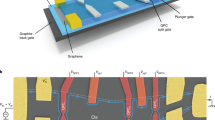
We designed a graphene-based FP interferometer tuned by a local gate array (Fig. 1a). The FP cavity is defined electrostatically using separated graphite top-gates (Methods and Supplementary Fig. 1), which ensures a high channel quality and allows a high degree of density tunability in-situ. Metal bridges contact each top-gate, and we additionally suspend metal bridges over the two quantum point contacts (QPCs), illustrated in Fig. 1b. By applying voltages \({V}_{{{\rm{QPC}}}1}\) and \({V}_{{{\rm{QPC}}}2}\) to these suspended bridge gates, we can tune the transmission of each QPC independently while keeping the filling factor of the surrounding regions fixed (Supplementary Note 1).

Fig. 1: Highly tunable Fabry-Pérot interferometer in graphene.
figure 1

a False-color scanning electron microscopy image of a Fabry-Pérot (FP) device identical to the device measured here. The graphite top-gate layer is selectively etched to form 8 separated top-gates (purple). Metal bridges (blue) connect to each graphite top-gate region and two additional bridges (yellow) suspend over the quantum point contacts (QPCs). The lithographic area of the interferometer cavity (area \(A=1.16\mu {{\mbox{m}}}^{2}\)) is defined by the central hexagonal top-gate. Scale bar: \(1{{\rm{\mu }}}{{\rm{m}}}\). b Simplified schematic of the FP tuned so that filling factors \({\nu }_{{{\rm{LG}}}}={\nu }_{{{\rm{MG}}}}{=\nu }_{{{\rm{RG}}}}=2\) and \({\nu }_{{{\rm{SG}}}1}={\nu }_{{{\rm{PG}}}}{=\nu }_{{{\rm{SG}}}2}=0\) illustrating interference of the partitioned outer edge channel (EC) (red) while the inner EC (blue) forms a closed annulus inside the FP. Voltage \({V}_{{{\rm{i}}}}\) applied to the top-gate labeled ‘i’ tunes the local filling factor \({\nu }_{{{\rm{i}}}}\). Voltages \({V}_{{{\rm{QPC}}}1}\) and \({V}_{{{\rm{QPC}}}2}\) applied to the suspended metal bridges selectively gate the QPC constrictions through the etched graphite gaps, tuning the QPC transmissions. We measure the diagonal conductance \({G}_{{{\rm{D}}}}={I}_{{{\rm{d}}}}/({V}_{{{\rm{D}}}}^{+}-{V}_{{{\rm{D}}}}^{-})\), where \({V}_{{{\rm{D}}}}^{\pm }\) and \({I}_{{{\rm{d}}}}\) are measured voltages in \((\pm )\) probes and drained current, respectively. See Supplementary Fig. 1 for the full device details. In addition to magnetic field, we tune the interference phase using voltage \({V}_{{{\rm{MG}}}}\) on the ‘middle gate’ or \({V}_{{{\rm{PG}}}}\) on the ‘plunger gate’. c Conductance as a function of \({V}_{{{\rm{QPC}}}1}\) with \({V}_{{{\rm{QPC}}}2}=7{{\rm{V}}}\) (i.e. \({T}_{{{\rm{QPC}}}2}=2\)) demonstrating QPC1 tunings to interfere outer EC (red dot) and inner EC (blue dot) in \(\nu=2\). See Supplementary Fig. 3 for QPC tuning details and voltages set on the other gates to form the necessary QPC saddle-points to acquire this data. d Same type of plot as (c), but demonstrating QPC2 operation instead of QPC1. e, f Characteristic FP oscillations as a function of \({V}_{{{\rm{PG}}}}\) for the inner EC and outer EC, respectively, at the QPC tunings indicated in (c) and (d). Vertical dashed lines indicate edges of plateaus of filling factor \({\nu }_{{{\rm{PG}}}}\). All data is at fixed magnetic field \(B=6{{\rm{T}}}\).

Full size image

In our experiments, we measure the diagonal conductance \({G}_{{{\rm{D}}}}\), as defined in Fig. 1b and Supplementary Fig. 1. In the regime that we study, \({G}_{{{\rm{D}}}}=\frac{{e}^{2}}{h}{\nu }_{{{\rm{QPC}}}}\) where \({\nu }_{{{\rm{QPC}}}}\) counts the number of edge channels transmitted through the device, with a partially transmitted channel counted as fraction34,35. To characterize the QPC transmissions, we measure \({G}_{{{\rm{D}}}}\) as a function of the bottom-gate voltage and split-gate voltage for each QPC with the bulk of the interferometer tuned to \(\nu=2\) at \(B=6{{\rm{T}}}\) (Supplementary Fig. 3). At \(\nu=2\), there are two spin-split Landau levels, of which the lower energy spin species hosts an EC closer to the effective boundary of the sample. Hence, we refer to the EC belonging to the lower (higher) energy spin species as the ‘outer’ (‘inner’) EC. Once appropriate bottom-gate and split-gate voltages are set, we tune \({V}_{{{\rm{QPC}}}1}\) and \({V}_{{{\rm{QPC}}}2}\), voltages applied on the suspended bridges to control the individual QPC transmissions. Figure 1c, d shows the measured \({G}_{{{\rm{D}}}}\) as a function of \({V}_{{{\rm{QPC}}}1}\) and \({V}_{{{\rm{QPC}}}2}\), respectively, with the other QPC fully open (i.e. \({\nu }_{{{\rm{QPC}}}2}=2\) and \({\nu }_{{{\rm{QPC}}}1}=2\), respectively). \({G}_{{{\rm{D}}}}\) exhibits plateaus at \(({\mathrm{0,1,2}})\frac{{e}^{2}}{h}\), corresponding to (neither, outer, both) ECs transmitted. In this regime, we define \({{T}_{{{\rm{QPC}}}}\equiv G}_{{{\rm{D}}}}\frac{h}{{e}^{2}}\) as the transmission of the QPC34, where \({0 \, < \, T}_{{{\rm{QPC}}}} \, < \, 1\) corresponds to a partially transmitted outer EC and \({1 \, < \, T}_{{{\rm{QPC}}}} \, < \, 2\) corresponds to a partially transmitted inner EC.

Tuning to partial transmission of the inner EC for both QPCs, \({T}_{{{\rm{QPC}}}1}={T}_{{{\rm{QPC}}}2}=1.5\), we observe high-visibility conductance oscillations as a function of plunger gate voltage \({V}_{{{\rm{PG}}}}\), which tunes the filling factor \({\nu }_{{{\rm{PG}}}}\) under the plunger gate, in Fig. 1e. Similarly, we tune to \({T}_{{{\rm{QPC}}}1}={T}_{{{\rm{QPC}}}2}=0.5\) and measure conductance oscillations on the outer EC in Fig. 1f. In both cases, oscillations are largest for \({\nu }_{{{\rm{PG}}}} \, < \, 0\), which corresponds to a fully gate-defined interference path since electrons are depleted under the plunger gate. Increasing \({\nu }_{{{\rm{PG}}}}\) brings the interfering edge closer to the etched graphene boundary, inducing dephasing18. Notably, the inner EC oscillations survive until \({\nu }_{{{\rm{PG}}}}=2\), when it flows close to the etched boundary of the graphene, while the outer EC reaches the boundary by \({\nu }_{{{\rm{PG}}}}=1.\) Another difference is the apparent irregularity of the oscillations on the outer EC compared to the inner EC, which we will understand in this work.

Phase jumps and AB oscillation frequency transition

High-visibility oscillations allow us to probe the dependence of interference phase \(\theta\) on magnetic field variation \(\delta B\) and gate voltage variations, which distinguishes the AB from the CD regimes13,15,18,19,22. For small variations in field and gate voltages in the AB regime, we expect \({\delta \theta /2\pi \, \approx \, A\delta B/{\Phi }_{0}+C}_{{{\rm{PG}}}}\delta {V}_{{{\rm{PG}}}}/e+{C}_{{{\rm{MG}}}}\delta {V}_{{{\rm{MG}}}}/e\), where \(A\), \({C}_{{{\rm{PG}}}}\), and \({C}_{{{\rm{MG}}}}\), are the (approximately constant) area enclosed by the interfering EC, interfering EC—plunger gate capacitance, and interfering EC – middle gate capacitance, respectively. Importantly, \({V}_{{{\rm{MG}}}}\) also directly tunes the electron density in the interferometer, so sweeping \({V}_{{{\rm{MG}}}}\) over a large range will change the FP cavity filling factor \({\nu }_{{{\rm{MG}}}}\). To calibrate the filling that we expect in the cavity, we first measure standard Hall conductance in the region gated by \({V}_{{{\rm{LG}}}}\) (see Supplementary Fig. 1e) and observe conductance plateaus (Fig. 2a). Since the top gates are identically coupled to the channel directly beneath them, an identical sweep of \({V}_{{{\rm{MG}}}}\) will tune \({\nu }_{{MG}}\) through the same filling factors. Data in the remaining panels of Fig. 2 were taken with the QPCs set to \({T}_{{{\rm{QPC}}}1}={T}_{{{\rm{QPC}}}2}=0.5\) i.e. partially transmitting the outer EC. Near the lowest density of the \({\nu }_{{MG}}=2\) plateau (Fig. 2b), we observe a typical AB interference pattern. Constant phase stripes \((\delta \theta=0)\) trace out a negative slope \(\delta {V}_{{{\rm{PG}}}}/\delta B\) with magnetic field period \(\Delta B\) yielding \({\Phi }_{0}/\Delta B=1.13\mu {{\mbox{m}}}^{2},\) matching the designed area \(A=1.16\mu {{\mbox{m}}}^{2}\). Plunger gate period \(\Delta {V}_{{{\rm{PG}}}}\) yields \(1/\Delta {V}_{{{\rm{PG}}}}=19.2{{{\rm{V}}}}^{-1}\). Increasing \({\nu }_{{MG}}\) using \({V}_{{{\rm{MG}}}}\) reveals more complicated interference patterns in Fig. 2c, d. Periodic shifts in the interference pattern persist and modulate until near the center of \({\nu }_{{MG}}=4\), as seen in Fig. 2e, when a simple stripe pattern returns. However, now \({\Phi }_{0}/\Delta B=2.32\mu {{\mbox{m}}}^{2}\) and \(1/\Delta {V}_{{{\rm{PG}}}}=36.3{{{\rm{V}}}}^{-1}\), both approximately doubled from Fig. 2b. Since \(A\) is fixed, a doubling of \({\Phi }_{0}/\Delta B\) indicates oscillations with \({\Phi }_{0}/2=h/2e\) periodicity instead of \({\Phi }_{0}\) so that \({\Phi }_{0}/2\Delta B=1.16\mu {{\mbox{m}}}^{2}\). Similarly, assuming a fixed \({C}_{{{\rm{PG}}}}\), then \(1/\Delta {V}_{{{\rm{PG}}}}\) doubling corresponds to adding twice as many electrons to the system per flux quanta. Both could be interpreted as an effective charge \({e}^{*}=2e\) for the interfering particle, as argued in GaAs25,26,27, but our observations indicate a different interpretation in our graphene-based interferometer.

Fig. 2: Density-tuned Aharonov-Bohm frequency doubling transition of outer EC.
figure 2

a Hall conductance \({G}_{{{\rm{xy}}}}\) in the region gated by \({V}_{{{\rm{LG}}}}\), demonstrating that \({V}_{{{\rm{LG}}}}\) (equivalently, any of the top gates) tunes the filling \(\nu\) underneath it at a fixed magnetic field \(B=6{{\rm{T}}}\). Colored dots indicate the filling (set by equivalent \({V}_{{{\rm{MG}}}}\) voltages) at which interference data are shown in (b–e); vertical dashed lines show the range of \({V}_{{{\rm{MG}}}}\) swept for (f). Top inset: schematic of compressible regions expected in the FP cavity when \({V}_{{{\rm{MG}}}}\) is swept. b–e Conductance \({G}_{{{\rm{D}}}}\) oscillations on the outer EC with \({V}_{{{\rm{PG}}}}\) and \(B\), for each of the indicated \({V}_{{{\rm{MG}}}}\) values. f \({G}_{{{\rm{D}}}}\) oscillations on the outer EC with \({V}_{{{\rm{PG}}}}\) and \({V}_{{{\rm{MG}}}}\), for \({V}_{{{\rm{MG}}}}\) swept continuously over the transition from apparent \(h/e\) to \(h/2e\) oscillations periodicity, at \(B=6{{\rm{T}}}\). \({G}_{{{\rm{D}}}}\) is plotted as a percentage of \(\frac{{e}^{2}}{h}\) deviation from the average value calculated for each fixed \({V}_{{{\rm{MG}}}}\) linecut and subtracted off. Further phase jumps or periodicity changes are not observed past \({V}_{{{\rm{MG}}}} \, \approx \, 1.7{{\rm{V}}}\) (checked up to \(\nu=7\)). QPCs are retuned to maintain transmissions \({T}_{{{\rm{QPC}}}1}={T}_{{{\rm{QPC}}}2}=0.5\) over the dataset while \({\nu }_{{{\rm{LG}}}}{=\nu }_{{{\rm{RG}}}}=2\) and \({\nu }_{{{\rm{SG}}}1}{=\nu }_{{{\rm{SG}}}2}=0\) are fixed.

Full size image

Importantly, we can observe the entire density-tuned transition to the AB frequency-doubled regime at fixed \(B\) by sweeping \({V}_{{{\rm{MG}}}}\) and observing oscillations with \({V}_{{{\rm{PG}}}}\), as shown in Fig. 2f. Remarkably, the frequency transition occurs continuously. From the top panel, \({\Phi }_{0}\) interference is apparent. As \({V}_{{{\rm{MG}}}}\) increases, periodic phase jumps begin to appear. Both the \({V}_{{{\rm{MG}}}}\) spacing and magnitude of the phase jumps increase, until eventually the most apparent periodicity corresponds to \({\Phi }_{0}/2\) oscillations (i.e., doubled frequency \({2\Phi }_{0}^{-1}\)).

To better understand the phase jumps, we use a general relation between charge and phase in FP interferometers36. When a single EC passes through the two constrictions with weak backscattering, the interference phase seen by the device at zero temperature is \(\theta=2\pi Q+{\theta }_{0},\, {\mathrm{mod}} \, 2\pi\), where \(Q\) is the total electron charge (in units \(e\)) in the region between the two scattering points and \({\theta }_{0}\) is a constant for small variations in \(B\), \({V}_{{{\rm{PG}}}}\), and \({V}_{{{\rm{MG}}}}\). In our experimental regime, \(\nu \ge 2\), we expect this relation to hold with \(Q={Q}_{1}+{Q}_{2}\), where \({Q}_{1}\) is the total charge residing in the lowest spin-split Landau level and \({Q}_{2}\) is the charge in the higher energy spin state (and also higher Landau levels). \({Q}_{1}\) can vary continuously since the outer EC is connected to the source and drain charge reservoirs. In contrast, \({Q}_{2}\) is required to be integer, as the corresponding energy levels are isolated through the incompressible QHE bulk. An integral change in \({Q}_{2}\) has no observable effect on the interference signal unless it produces a non-integral change in \({Q}_{1}\) due to Coulomb coupling between the two types of charge. Hence, we can redefine \(\theta\) to include only the charge \({Q}_{1}\) in the lowest spin-split Landau level, and the values \({Q}_{1}\) in the ground state of the interferometer determine \(\theta\). Following similar models used to understand the CD regime15,24,37 and considering small changes in \({Q}_{1}\) and \({Q}_{2}\), we expand the change in ground state energy \(E={K}_{1}{\delta {Q}_{1}}^{2}+{K}_{2}{\delta {Q}_{2}}^{2}+{2K}_{12}\delta {Q}_{1}\delta {Q}_{2}\), where \({K}_{i}\) is the charging energy of the charge species \(i\) and \({K}_{12}\) describes the mutual capacitive coupling between them. Energetic stability requires that \({\left|{K}_{12}\right|}^{2}\le {K}_{1}{K}_{2}\). Within this capacitive coupling model, when \({Q}_{2}\) increases by 1, the charge \({Q}_{1}\) correspondingly decreases by a discrete (generically non-integral) amount \(\Delta {Q}_{1}\) to screen the added charge, leading to a phase shift \(\Delta \theta /2\pi=\Delta {Q}_{1}={-} {K}_{12}/{K}_{1}\).

By taking 1D fast Fourier transforms (FFTs) along lines parallel to the phase jumps14,15, we extract several values of \(\Delta \theta /2\pi\) near the center of the periodicity transition in Fig. 3a. We observe that the locations where the phase jumps occur (marked in Fig. 3b) follow a steeper slope than the slope \({\delta V}_{{{\rm{PG}}}}\)/\({\delta V}_{{{\rm{MG}}}}\) of constant phase lines of the main interference oscillation in the \({V}_{{{\rm{MG}}}}\)-\({V}_{{{\rm{PG}}}}\) planes. A steeper slope also occurs in the \(B\)-\({V}_{{{\rm{PG}}}}\) plane (Fig. 2c, d). Moreover, these phase jump lines have negative slopes \({\delta V}_{{{\rm{PG}}}}/\delta B \, < \, 0\), like the constant phase lines of AB oscillations. This observation is in sharp contrast to the phase jumps reported in the FP interferometer operated in the fractional QHE regime14,15 or in the FP interferometer operated in the integer CD regime37, where phase jump lines follow positive slope \({\delta V}_{{{\rm{PG}}}}/\delta B > 0\). The different slope suggests a different structure to the energy levels that are being populated in our sample. Considering that the outer EC is partitioned at the QPCs, while the inner ECs are well isolated, we hypothesize that the charging events seen as phase jumps represent charge added to the annular, closed inner EC, illustrated in Fig. 3. The dominant coupling \({K}_{12}\) is directly between the outer and inner \(\nu=2\) ECs. Any charges added to higher Landau levels or to localized states in the bulk are not measurably coupled to the outer EC, presumably because of effective screening by the gates.

Fig. 3: Phase jump extraction in the transition regime.
figure 3

a Phase \(\theta\) of the 1D FFT extracted along linecuts parallel to the phase jumps in (b). The phase is evaluated at the dominant frequency in the FFT amplitude spectrum for the linecuts in between phase jumps. A linear increase in phase extracted from regions without phase jumps is subtracted off to make the phase jump magnitude evident as the vertical shift between plateaus in panel (a). From this data we extract an average \(\Delta \theta /2\pi \, \approx \, -0.47,\) reflecting approximately half of an electron repelled from the outer EC for each charge added to the inner EC within this range of \({V}_{{{\rm{MG}}}}\). Inset: illustration of the coupling \({K}_{12}\) between the outer and inner ECs contributing to the phase jumps. b Conductance \({G}_{{{\rm{D}}}}\) oscillations on the outer EC with \({V}_{{{\rm{PG}}}}\) and \({V}_{{{\rm{MG}}}}\) near the center of the transition regime showing periodic phase jumps along the dashed black lines. Note that increasing \({V}_{{{\rm{MG}}}}\) adds electrons to the system or equivalently increases phase, so the phase jumps correspond to negative shifts in phase i.e., repulsion of electrons from the FP cavity. Similar interference patterns are observed in both the strong and weak QPC backscattering regimes (Supplementary Fig. 4) as well as at elevated temperatures (Supplementary Fig. 5).

Full size image

AB frequency doubling from strongly coupled QHE edge states

We provide further evidence for capacitively coupled QHE edges tuning the AB frequency in Fig. 4. At fixed \({V}_{{{\rm{MG}}}}\) in the transition regime, we compare interference in the \(B\)-\({V}_{{{\rm{PG}}}}\) plane for the inner EC, Fig. 4a, to the outer EC, Fig. 4c. This direct comparison is only possible because we can control QPC transmissions independently of bulk filling. We observe that the slope of the oscillation maxima on the inner EC (dotted lines in Fig. 4a) matches the slope of the phase jump lines on the outer EC (dotted lines in Fig. 4c). Reducing the transmission for the inner EC, the interference maxima in Fig. 4a become sharper charging resonances, corresponding to charge \({Q}_{2}\to {Q}_{2}+1\) through the inner EC. When the transmission of the inner EC vanishes, the inner EC is fully disconnected from the source and drain charge reservoirs, and the outer EC is now partitioned at the QPCs to form a new interference path (shown in the left inset in Fig. 4c). Since the bulk density and electrostatic configurations for Fig. 4a and Fig. 4c are identical, the regions in between the phase jump lines in Fig. 4c correspond to fixed \({Q}_{2}\), and we see that the interference phase on the outer EC shifts when the charge on the inner EC discretely changes.

Fig. 4: Comparison of inner and outer EC interference and couplings across transition.
figure 4

a Conductance \({G}_{{{\rm{D}}}}\) oscillations on the inner EC (\({T}_{{{\rm{QPC}}}1}={T}_{{{\rm{QPC}}}2}=1.5\)) with \({V}_{{{\rm{PG}}}}\) and \(B\), for \({V}_{{{\rm{MG}}}}=1.2{{\rm{V}}}\). Dotted black lines highlight conductance maxima. Left inset: illustration of inner EC interference configuration. b 2D FFT of the \({G}_{{{\rm{D}}}}\) oscillations in (a) showing peak \({{{\boldsymbol{f}}}}_{{{\rm{i}}}}\) (vector corresponding to blue arrows) and its harmonics, where \({\Phi }_{0}\equiv h/e\). c \({G}_{{{\rm{D}}}}\) oscillations on the outer EC (\({T}_{{{\rm{QPC}}}1}={T}_{{{\rm{QPC}}}2}=0.5\)) at the same density set by \({V}_{{{\rm{MG}}}}\). Dotted black lines with identical slope to (a) highlight phase jumps. Left inset: illustration of outer EC interference configuration. d 2D FFT of oscillations in (c) showing the peaks \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\) (red arrows), \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\), and \({{{\boldsymbol{f}}}}_{{{\rm{o}}}-{{\rm{i}}}}\) and their harmonics. e Magnitude of the phase jump on the outer EC as a function of \({V}_{{{\rm{MG}}}}\). Each data point is averaged over a \(\sim 0.25{{\rm{V}}}\) range in \({V}_{{{\rm{MG}}}}\); error bars indicate \(\pm 1\) standard deviation in this range. Unfilled data points represent zero observable phase jumps over the range, hence we infer a magnitude of \(0\) or \(-1\). \({G}_{{{\rm{xy}}}}\) of the device taken in an identical measurement to Fig. 2a, reflecting the expected filling \({\nu }_{{{\rm{MG}}}}\), is plotted for reference. Top inset: cartoon of the outer and inner EC evolution with increasing \({V}_{{{\rm{MG}}}}\). f Magnitudes \({I}_{{{\rm{o}}}}\), \({I}_{{{\rm{o}}}+{{\rm{i}}}}\), and \({I}_{{{\rm{o}}}-{{\rm{i}}}}\) of the respective peaks \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\), \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\), and \({{{\boldsymbol{f}}}}_{{{\rm{o}}}-{{\rm{i}}}}\) as a function of \({V}_{{{\rm{MG}}}}\). \({I}_{{{\rm{o}}}}\), \({I}_{{{\rm{o}}}+{{\rm{i}}}}\), and \({I}_{{{\rm{o}}}-{{\rm{i}}}}\) are normalized by the sum \({I}_{{{\rm{o}}}}+{I}_{{{\rm{o}}}+{{\rm{i}}}}+{I}_{{{\rm{o}}}-{{\rm{i}}}}\) to show their relative contributions. Each data point is extracted from a 2D FFT (Supplementary Fig. 7). g Magnetic field frequency multiplied by \({\Phi }_{0}\) for peaks \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\), \({{{\boldsymbol{f}}}}_{{{\rm{i}}}}\), \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\), and \({{{\boldsymbol{f}}}}_{{{\rm{o}}}-{{\rm{i}}}}\) tracked through the transition. Note that \({{{\boldsymbol{f}}}}_{{{\rm{i}}}}\) is measured from a separate measurement of interference on the inner EC (Supplementary Fig. 8). h Same as (g) but for plunger gate frequency. Horizontal dashed lines in (g, h) indicate the corresponding \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\) and \({2{{\boldsymbol{f}}}}_{{{\rm{o}}}}\) values before the transition. Black (red) dots show calculated \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\pm {{{\boldsymbol{f}}}}_{{{\rm{i}}}}\) from outer and inner EC data, which match the peaks identified as \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\) and \({{{\boldsymbol{f}}}}_{{{\rm{o}}}-{{\rm{i}}}}\), respectively.

Full size image

Taking Fourier transform of the interference signal provides further understanding of interactions between the two ECs involved in the interference. Figure 4b, d shows the 2D FFT of the conductance oscillations in Fig. 4a, c. For interference of the inner EC (Fig. 4b), we observe a simple FFT pattern of peaks corresponding to the fundamental frequency of the inner EC \({{{\boldsymbol{f}}}}_{{{\rm{i}}}}\), a vector containing the peak position in the 2D FFT, and its harmonics (\({n{{\boldsymbol{f}}}}_{{{\rm{i}}}}\), where \(n\) is an integer). The FFT pattern of the outer EC interference (Fig. 4d) exhibits a more complicated lattice of Fourier peaks. If we label one of the dominant peaks as the fundamental frequency of the outer EC, \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\), we can then identify the rest of the peaks by addition or subtraction of the same vector \({{{\boldsymbol{f}}}}_{{{\rm{i}}}}\) evident in the inner EC data. The lowest order peaks correspond to the sum \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}={{{\boldsymbol{f}}}}_{{{\rm{o}}}}+{{{\boldsymbol{f}}}}_{{{\rm{i}}}}\) and the difference \({{{\boldsymbol{f}}}}_{{{\rm{o}}}-{{\rm{i}}}}={{{\boldsymbol{f}}}}_{{{\rm{o}}}}-{{{\boldsymbol{f}}}}_{{{\rm{i}}}}\). We show a similar Fourier lattice construction in Supplementary Fig. 6 for interference in the \(B\)-\({V}_{{{\rm{MG}}}}\) plane.

By tuning \({V}_{{{\rm{MG}}}}\), we modulate the filling factor of the interferometer cavity in a wide range and observe the evolution of the interference patterns and corresponding peaks for the outer (inner) EC in Supplementary Fig. 7 (8). As in Fig. 2, phase jumps appear only within the periodicity transition. Figure 4e shows the average magnitude of individual phase jumps as a function of \({V}_{{{\rm{MG}}}}\). We find that the phase jump continuously evolves from \(\Delta \theta /2\pi \, \approx \, 0\) (\({V}_{{{\rm{MG}}}} \, < \, 0.6{{\rm{V}}}\)) through the periodicity transition to \(\Delta \theta /2\pi \, \approx \, {-}1\)(\({V}_{{{\rm{MG}}}} \, > \, 1.6{{\rm{V}}}\)), corresponding to the strongly coupled limit \({K}_{12}/{K}_{1} \, \approx \, 1\). The transition regime marked by non-trivial phase jumps spans from the appearance of the inner EC (\({V}_{{{\rm{MG}}}} \, \approx \, 0.6{{\rm{V}}}\)) to the strongly coupled outer two EC limit (\({V}_{{{\rm{MG}}}} \, \approx \, 1.6{{\rm{V}}}\)).

The Fourier peaks’ evolution tuned by \({V}_{{{\rm{MG}}}}\) provides further insight into the interaction between ECs. Figure 4f displays the normalized Fourier peak intensity as a function of \({V}_{{{\rm{MG}}}}\).The amplitude of the Fourier peak \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\) decays through the transition regime (\({0.6{{\rm{V}}} \, < \, V}_{{{\rm{MG}}}} \, < \, 1.6{{\rm{V}}}\)), replaced by \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\) as the dominant peak. We plot the magnetic field frequency multiplied by \({\Phi }_{0}\) (Fig. 4g) and the plunger gate frequency (Fig. 4h), respectively, for each of the lowest-order peaks \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\), \({{{\boldsymbol{f}}}}_{{{\rm{i}}}}\), \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\), and \({{{\boldsymbol{f}}}}_{{{\rm{o}}}-{{\rm{i}}}}\) as a function of \({V}_{{{\rm{MG}}}}\). At the beginning of the transition regime where the ECs are not interacting, both \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\) and \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\) approach the corresponding AB frequency \({\Phi }_{0}^{-1}=e/h\) through the designed area. As \({V}_{{{\rm{MG}}}}\) increases, however, \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\) stays nearly unchanged, while \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\) increases to reach the doubled value \({2\Phi }_{0}^{-1}\). The experimental observation that the dominant peak in the frequency-doubled regime corresponds to \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\) precludes the possibility of \(2e\) charge pairing within the outer EC alone.

Instead, our frequency-doubled regime arises from Coulomb interaction between the spin-split ECs combined with charge quantization on the inner EC (Methods). Electrons would naturally tend to enter the inner EC at frequency \({{{\boldsymbol{f}}}}_{{{\rm{i}}}}\), but, due to charge quantization, cannot enter continuously. Hence, as the magnetic flux increases continuously, the area enclosed by the inner EC must shrink to maintain fixed charge. During this shrinking process, electron charge is transferred continuously into the interior, leaving missing electron charge between the outer and inner ECs. In the strongly coupled EC limit, this missing charge attracts an equal charge onto the outer EC for screening. In the absence of this screening effect, charge is continuously added to the outer EC with frequency \({{{\boldsymbol{f}}}}_{{{\rm{o}}}}\) according to the increased AB phase. In the coupled ECs, the combination of the screening-induced charge and the natural AB effect results in the outer EC charging at a frequency \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\). Therefore, the interference phase follows \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\). In addition to this continuous charging effect, electrons can tunnel into the inner EC from the external reservoirs. As previously discussed, each electron addition repels some electron charge from the outer EC, causing the negative interference phase shifts that we observed. For larger values of \({V}_{{{\rm{MG}}}}\), as the bulk density increases, the inner and outer EC move closer together, and the system approaches the strong coupling limit, where the phase jumps are close to \(-2\pi\) and unobservable, reflecting a full electron charge screening. Moreover, as the inner and outer ECs asymptotically enclose the same area, set by the confining potential of the device, the frequency \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\) approaches \({2\Phi }_{0}^{-1}\).

Note: a concurrent work also observed apparent AB frequency tripling, corresponding to the sum of the three \(\nu=3\) edge channel frequencies38. The framework that we developed here can be expected to naturally explain this observation, since in devices utilizing the graphene crystal edge, the sharp confining potential can lead to multiple ECs developing within a few magnetic lengths of the edge8. The combination of reduced spatial separation and reduced screening by nearby graphite gates may account for the observation of apparent tripling, arising from the outer EC screening both internal localized ECs.

Discussion

We have investigated phase jumps and AB frequency modulation in a highly tunable graphene QHE FP interferometer with coupled co-propagating edge modes. We identify that interference phase jumps are related to the single electron charging events in the inner EC, and the transition of the AB frequency can be connected to the corresponding screening effect of the outer EC. As \({V}_{{{\rm{MG}}}}\) increases, the EC coupling becomes strong and the AB frequency doubles, indicating a near-perfect screening between the ECs. Thus, our experimental observation supports the proposal that AB frequency doubling can be explained without explicitly introducing electron pairing within the outer two ECs33. In other words, a half flux quantum introduced in the two strongly coupled ECs can bring a full charge from the external reservoir and a \(2\pi\) evolution of the observed interferometer phase.

Our observations do not exclude the possibility of further correlation effects in the strongly coupled ECs; instead, the tunably coupled ECs discovered here provide a system to test the emergence of electron correlations in 1D systems39. However, AB frequency multiplication, which we explained within a single particle picture, cannot substantiate the correlation effect. Further experiments probing the transition from the weakly to strongly coupled limit, such as shot noise25,40,41, finite-bias dependence15,42, energy relaxation43, and high-frequency transport44,45,46 will provide further insight into the ground state and excitations. More generally, inter-edge screening could affect interferometry in fractional fillings containing multiple ECs42,47,48,49, though fractional QHE experiments so far appear to be in the weak coupling regime42,50. The recent observations of interference in fractional quantum Hall states using similar bilayer and monolayer graphene devices51,52,53 will enable further experiments to probe the interacting co-propagating fractional QHE edge modes, where it remains unclear whether the strong coupling regime can be realized between fractional edge channels.

Methods

Sample preparation

The monolayer graphene stacks with hBN and graphite encapsulation used in this study were fabricated using the standard polycarbonate (PC) polymer dry transfer method (ref. 18). The graphite top-gates and bottom-gate, which encapsulate the graphene channel after stacking, are crucial to screen charge disorder from the graphene channel, stabilizing robust integer and fractional QHE states at low magnetic fields (Supplementary Fig. 2). The stack used for all data shown here had a top (bottom) hBN thickness of 49 (27) nm. After adhering the stack to a substrate and annealing in vacuum at 300 °C, the top gate was first etched into a simplified shape by reactive ion etching in an inductively coupled plasma etching chamber with 30 W O2 plasma using a polymethyl methacrylate (PMMA) resist patterned with electron-beam lithography as the etch mask. Next, a full etch through the entire stack was performed to define all outer boundaries. This etching was in several steps: first a pure 30 W O2 etch remnants of the top graphite; then a 30 W process O2/CHF3 to etch through the underlying hBN, graphene, and hBN; and finally another 30 W O2 etch to remove the bottom graphite. Next, edge contacts to the exposed graphene were made by a 30 W CHF3 etch on the exposed hBN/graphene/hBN contact regions and thermal evaporating 2/7/150 nm of Cr/Pd/Au at an angle with rotation. Then, air bridge contacts were made to the top-graphite in various locations using a bilayer PMMA process followed by a short 20–25 s 30 W O2 plasma PMMA residue clean and thermal evaporation of 2/7/350 nm Cr/Pd/Au. Then, to etch the ~100 nm width trenches to separate the top graphite regions, a thinner PMMA resist was used and again a reactive ion etch with gentle 30 W O2 plasma alone was done in ~1 minute steps. In between etches, the two-probe resistance between each bridge-contacted gate was checked until they were all separated. Finally, bridge contacts to the separated central hexagon gate and suspended bridges over the QPC regions were deposited. See Supplementary Fig. 1 for more details on the fabrication process and the final device.

Measurements

The 8 top graphite gates in the device were separately controlled to set filling factors in each region at perpendicular magnetic field B, since Landau level filling factor (also simply called ‘filling’) \(\nu \equiv {n}_{e}/{n}_{\phi }\), where \({n}_{\phi }={{\rm{e}}}B/h\) and \({n}_{e}\) is the areal electron density. At the region in the middle of the top-gate split-gates, where the graphite is etched away for a separation of ~150 nm, the electrostatics are tuned to create a saddle-point potential at the QPC. See Supplementary Note 1 for details of this tuning process. Once an approximate saddle-point is formed at the QPCs using the graphite top-gates and bottom-gate, the suspended metal bridges over the QPCs are tuned to precisely set transmissions \({T}_{{{\rm{QPC}}}1}\) and \({T}_{{{\rm{QPC}}}2}\). The neighboring top-gates screen out stray fields generated by the suspended bridges such that \({V}_{{{\rm{QPC}}}1}\) and \({V}_{{{\rm{QPC}}}2}\) are primarily coupled to the graphene at the saddle-point of the QPCs. We interpret non-integer values \(0 < {T}_{{{\rm{QPC}}}} < 1\) as a transmission probability for electrons in the outer EC, which is partially transmitted, while for \(1 \, < \, {T}_{{{\rm{QPC}}}} \, < \, 2\), \({T}_{{{\rm{QPC}}}}-1\) gives the transmission probability for the inner EC.

Experiments were performed in an Oxford wet dilution system with base temperature ~20 mK and estimated ~20–25 mK electron temperature. The 24 DC measurement lines of the fridge were carefully thermalized through Thermocoax cables and 3 Sapphire plates between room temperature and the mixing chamber. A series of lumped element Pi and RC filters at the mixing chamber reduced electronic noise and ensured low electron temperature. Unless otherwise noted, a constant 6 T perpendicular magnetic field was applied. Measurements were taken using standard low-frequency lock-in amplifier techniques with a typical AC excitation current of 1 nA at 17.77 Hz applied to the sample and simultaneously measured AC voltage drops and drained current. Graphite and suspended bridge gates were controlled with a house-made, low-noise 16-bit D/A voltage source. Bias dependence (see Supplementary Note 4) was taken by voltage biasing instead and adding in a DC bias at the source. Simultaneously, the DC voltage drop \({V}_{{{\rm{D}}}}\) was measured on the same probes measuring the AC conductance so that the accurate voltage drop across the FP cavity was known. All data collected and analysis programs have been made available.

Estimation of the coupling strength

Although we have not attempted a detailed calculation of the coupling constants important for our analysis, we can at least advance some qualitative arguments for the trend that emerges from our analysis. The edge of the sample consists of alternating compressible and incompressible stripes whose width is set by electrostatics6. ECs are located in compressible stripes. It may be expected that the outermost EC is located along an electron density contour where the local Landau-level filling factor is ~ 0.5, while the second EC is located along a contour with filling ~1.5. Due to residual disorder and electron-electron interactions, the Hall plateau at \(\nu=2\) will set in when the bulk filling is smaller than 2, though larger than 1.5. The density profile produced by charges on confining gates should be relatively smooth, so that the spatial separation between the outer most EC and the second EC should be relatively large at this point, and the Coulomb coupling between the channels, screened by the gates, should be relatively weak. As the electron density is increased, the inner EC should move closer to the outer edge, and the coupling should become stronger, and it is plausible that by the time the device enters the \(\nu=3\) plateau, the value of \({K}_{12}/{K}_{1}\) is close to 1.

Further increases in the density should produce additional ECs, which are totally reflected at the QPCs and do not contribute directly to the transport. The number of electrons on any additional closed ECs, as on other localized states, will be restricted to integer values, and in principle, due to Coulomb interactions, there should be a jump in the interference phase of outer edge states each time this integer changes by one. However, Coulomb interactions in our system are strongly screened by the nearby gates, so if the additional channels are not close to the outer two ECs, the jumps would be too small to be observable. In monolayer graphene, the energy gap at \(\nu=2\), which is due to the cyclotron energy, is much larger than the gaps at \(\nu=\) 1, 3, 4, and 5, which arise from electron-electron interactions. Consequently, we expect that the spatial separation between the outermost EC and the second EC will tend to be small compared to the separation between the second EC and any additional ECs.

Another issue is the stability criterion embodied in the requirement \({\left|{K}_{12}\right|}^{2} \, \le \, {K}_{1}{K}_{2}\). This requirement is automatically satisfied if we assume that when the two outer ECs are close together, the energy for adding an electron to either one of them is dominated by an electrostatic energy that depends primarily on the total charge on the edges, and only weakly on the difference between them, so that \(E=a{\delta {Q}_{1}}^{2}+b{\delta {Q}_{2}}^{2}+{2K}_{12}{(\delta {Q}_{1}+\delta {Q}_{2})}^{2}\), with \(a\) and \(b\) small compared to \({K}_{12}\). Then, \({K}_{1}\) and \({K}_{2}\) will be approximately equal to each other and slightly larger than \({K}_{12}\).

This analysis is compatible with experiments in GaAs interferometers where the ECs occur at the boundary between two QHE states of different integer filling fractions (ref. 27). There it was found that the \(h/2e\) periodicity occurred only if the outer EC and second EC belong to the same orbital Landau level, and not if they belong to different levels. In the first case, the energy gap for the QHE state between the two ECs will arise from electron-electron interactions, while the energy gap in the second case will be dominated by the generally larger cyclotron energy. Therefore, in the first case, when the density is increased enough to populate a third QHE state in the bulk of the sample, the two outer ECs might be pushed so close to each other that they are strongly coupled, while this might not be expected to happen in the second case.

Physics of AB frequency doubling at strong coupling

The meaning of the charge fluctuations \(\delta {Q}_{1}\) and \(\delta {Q}_{2}\) can be made more precise as follows. As stated in the main text, we define \({Q}_{1}\) as the number of electrons in the lowest spin-split Landau level enclosed by the outer edge mode and \({Q}_{2}\) as the number of electrons in the higher spin state enclosed by the inner mode. These charges are related to the enclosed areas \({A}_{1}\) and \({A}_{2}\) by \({Q}_{i}={A}_{i}B/{\Phi }_{0}\), where \(i=1\) or \(2\). These areas are allowed to deviate slightly from the ideal areas \({\bar{A}}_{i}\), which are assumed to be smooth functions of \({V}_{{{\rm{PG}}}}\) and, at most weakly varying functions of \(B\) and \({V}_{{{\rm{MG}}}}\). Then \(\delta {Q}_{i}={Q}_{i}-B{\bar{A}}_{i}/{\Phi }_{0}\), and the energy \(E\) may be expanded to quadratic order in \(\delta {Q}_{i}\) as stated above.

When the inner mode is completely reflected at the QPC, the charge \({Q}_{2}\) is constrained to be an integer, while the charge \({Q}_{1}\) can change continuously, assuming that the outer edge is mostly transmitted through the QPCs. At low temperatures the charges will be determined so as to minimize \(E\), subject to the integer constraint.

If \({Q}_{2}\) is held fixed while the magnetic field is increased by a small amount \(dB\), the inner edge charge \(\delta {Q}_{2}\) will change by an amount \(-dB{\bar{A}}_{2}/{\Phi }_{0}\). This happens because, as the area shrinks, charge is transferred from the edge region to the interior, where it is effectively screened by the gates, leaving a charge deficit at the edge. In the strong coupling limit, this will cause \(\delta {Q}_{1}\) to increase by an equal amount. Thus, the total charge \({Q}_{1}\) in the lowest spin-split Landau level will increase by \({{dQ}}_{1}=dB\left({\bar{A}}_{1}+{\bar{A}}_{2}\right)/{\Phi }_{0}\), and the interferometer phase \(\theta\) will increase by \({2\pi {dQ}}_{1}\).

If \(B\) is increased by a large amount, the value of \({Q}_{2}\) will not be fixed but will undergo periodic integer jumps. In the strong coupling limit, the jump in \({Q}_{1}\) caused by a jump in \({Q}_{2}\) will also be an integer. This will cause \(\theta\) to jump by a multiple of \(2\pi\), which will be invisible in an interferometer experiment. Thus, the observed rate of change of the phase will be \(d\theta /dB=2\pi \left({\bar{A}}_{1}+{\bar{A}}_{2}\right)/{\Phi }_{0}\), which is equal to \(4\pi {\bar{A}}_{1}/{\Phi }_{0}\), if we neglect the difference between \({\bar{A}}_{1}\) and \({\bar{A}}_{2}\). This rate of change is twice as fast as would have been observed in the absence of coupling between the inner and outer edge modes.

We remark that in the course of adding one flux quantum to the area \({\bar{A}}_{1}\), one would expect on average to have a jump by one electron in each spin state. So, in general, one will have one positive jump in \({Q}_{2}\) and one negative jump in \({Q}_{1}\). Thus, while the observed interference phase will change by an amount equivalent to a change of two electrons, the actual change in \({Q}_{1}\) will only be one electron.

Influence of bulk-edge coupling and screening by nearby gates

Screening of long-range Coulomb interactions by nearby gates in our device is essential to consider when determining the influence of edge-edge and bulk-edge coupling on the interference signal. In the data analysis and preceding discussion, we have neglected bulk-edge coupling since the radius of the interference loop extracted from the outer EC interference (~600 nm) is always much larger than the average distance to the graphite screening gates (~38 nm), as shown in Supplementary Fig. 9. Therefore, bulk-edge interaction should be well screened by the gates. In contrast, the distance between the inner and outer EC approaches ~85 nm in the strong-coupling limit, which enables strong Coulomb interaction that will not be screened out by the gates. We also observe that the contribution of edge-edge coupling, as evidenced by the presence of the \({{{\boldsymbol{f}}}}_{{{\rm{o}}}+{{\rm{i}}}}\) component in the signal, becomes significant only when the edge-edge separation becomes about 200 nm or less, within about a factor of 5 of the gate distance. The behavior of the inner EC interference over the range of density we explored is also consistent with these rough estimates, as the interference signal continues to show Aharonov-Bohm interference (Supplementary Fig. 8) through a shrinking area down to an enclosed radius of 200 nm. Hence, we find that bulk-edge coupling is negligible in all experimental regimes that we explored.

According to the model by Frigeri et al. (ref. 33), for negligible bulk-edge coupling, the transition to frequency doubling occurs when the inter-channel interaction drops to roughly half of the charging energy for a bare outer EC. This would correspond to the point where the inter-channel distance is comparable to the distance to the screening gates. We find that indeed this agrees with our data, since the system enters the strongly coupled limit when the average inter-channel separation approaches ~85 nm, approximately twice the average distance to the top and bottom gates (Supplementary Fig. 9).

Robustness of the theoretical predictions

As discussed in ref. 36, when a single EC passes through the two constrictions, with weak backscattering at the constrictions, the interference phase seen at low temperatures and low source-drain voltage is given by \(\theta=2\pi Q+{\theta }_{0},\, {\mathrm{mod}} \, 2\pi\), where \(Q\) is the total electron charge (in units \(e\)) in the region between the two scattering points (the expectation value of the charge on the interferometer in its ground state) and \({\theta }_{0}\) is a constant for small variations in \(B\), \({V}_{{{\rm{PG}}}}\), and \({V}_{{{\rm{MG}}}}\). The argument is essentially the same if the backscattering is not weak. The principal effect of stronger backscattering at the QPCs is to add a term to the energy \(E\) that favors integer values of the charge \({Q}_{1}\) and hence integer values of the total charge on the interferometer. This means that as the control parameters are varied continuously, the phase difference \(\theta -{\theta }_{0}\) will undergo an additional modulation pulling it towards the nearest integer multiple of \(2\pi\). If we define \({\theta }_{{{\rm{b}}}}\) as the value of the interferometer phase that would occur in the limit of weak backscattering, for the given value of the control parameters, then the actual value of \(\theta\) should have the form \(\theta={\theta }_{{{\rm{b}}}}+\delta \theta\), where \(\delta \theta\) is a periodic function of \({\theta }_{{{\rm{b}}}}-{\theta }_{0}\). In addition, in the presence of finite back scattering, interference contribution to the measured resistivity may no longer be a simple sinusoidal function of \(\theta\) but can contain higher harmonics. The combination of these effects means that the interference current will remain a periodic function of \({\theta }_{{{\rm{b}}}}\), with period \(2\pi\), but the relative amplitudes of various harmonics may be modified. In the main text, it was argued that \({\cos \theta }_{{{\rm{b}}}}\) should be a two-dimensional periodic function of \(B\) and the gate voltages, with frequencies expressed in terms of two non-colinear fundamental vectors in reciprocal parameter space. The effect of finite backscattering at the QPCs will be to modify the amplitudes of the various Fourier components, but not to change their positions.

Using similar arguments, we may argue that measurement at finite temperature should not change the locations of the fundamental frequency vectors, but thermal fluctuations will reduce the Fourier amplitudes. In general, at high temperatures \(T\), the amplitude of a given Fourier component will fall off, proportional to \({e}^{-T/\varepsilon }\), where \(\varepsilon\) will be different for each Fourier component. At sufficiently high temperatures, therefore, only the one or two components with the largest values of \(\varepsilon\) will remain visible. The values of \(\varepsilon\) will depend on details of the system, but typically the Fourier components that are most prominent at \(T=0\) will be the ones that persist to highest temperatures.

For our system, in the case where there is only a single EC, as we find for bulk filling less than 2, the value of \(\varepsilon\) for the lowest Fourier mode is predicted to be \(\varepsilon={hv}/(2{\pi }^{2}P)\), where \(v\) is the EC velocity and \(P\) is the perimeter of the interferometer path. For the case of two strongly coupled edge channels, the prediction is \(\varepsilon={hv}/(4{\pi }^{2}P)\), where \(v\) is now the velocity of the fast charge mode. In both cases, the dominant effects come from thermal fluctuations \(e\delta Q\) of the charge on the edge, whose energy cost is given by \({(e\delta Q)}^{2}/(2\gamma P)\), where \(\gamma\) is the capacitance per unit length of the edge. The velocity \(v\) is given by \(v=\delta {\sigma }_{{{\rm{xy}}}}/\gamma\), where \(\delta {\sigma }_{{{\rm{xy}}}}\) is the change in Hall conductance across the edge. Using our lithographically defined perimeter \(P=4.24{{\rm{\mu }}}{{\rm{m}}}\) and the velocity \({v}_{{{\rm{e}}}}=\frac{e\Delta {V}_{{{\rm{D}}}}P}{h}=1.46\times {10}^{5}{{\rm{m}}}/{{\rm{s}}}\) extracted from finite-bias dependence in the uncoupled case (Supplementary Fig. 11), we find \(\varepsilon=83.7{{\rm{mK}}}\), well above our estimated electron temperature.