Modelling universality and scaling

Abstract

Understanding the allocation of metabolic energy between the sustenance of an organism and its growth is an important issue in ecology. West et al.¹ have built on their earlier attempts to explain the exponent for the allometric scaling of metabolism and have derived a single, parameterless universal curve that describes the growth of many species. Here we show that the universal curve arises from general considerations that are independent of the specific allometric model used by West et al. and that the data do not distinguish between a 3/4 or 2/3 exponent in the relationship between metabolic rate and mass scaling.

Main

von Bertalanffy² (see his equation (5)) considered a general equation of the form dm/dt = a_αm^α−b_αm^β, where m is the body's mass at time t, and α and β are unspecified exponents, and a_α and b_α are positive coefficients. The equation considered by West et al.¹ is a special case, with α = 3/4 and β = 1, whereas von Bertalanffy studied the case with α = 2/3 and β = 1. Such an equation can be cast in a scaling form: dm/dt = m^αf(m/M), where M provides a scale for the organism's mass and is usually chosen to be the asymptotic maximum body size. The scaling function f approaches a constant value for a small argument — when m(t) is small compared with M, relatively little energy is required to sustain the organism and virtually all of the metabolic energy is funnelled into growth processes. The requirement that dm/dt = 0 when m reaches the value M leads to the condition that f(1) = 0.

Moreover, the initial condition of the mass at t = 0 being equal to the birth mass, m₀, must be satisfied. For von Bertalanffy's equation², f(x) = a_α(1 − x^1−α), with a_α = b_αM^1−α.

We have analysed the data of West et al.¹ on the cow, hen and guppy to assess whether it is possible to discriminate between the two choices for α. We find that their equation (5) (which is a special case of equation (6) of ref. 2), written in the form

or, equivalently, as

(with the dimensionless mass ratio r = (m/M)^1−α and the dimensionless time τ = $-\ln [[1-{({\mathrm{mml\_m}}_0/\mathrm{MML:M})}^{1-\alpha }]e^{-{\gamma }_{\alpha }t}]$), fits the observations equally well for both values of α (Fig. 1).

Figure 1: Growth curves for three different organisms and the collapse of mass scaling.

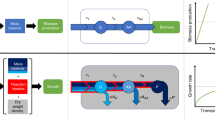
a–c, Growth curves for a, cow; b, guppy; and c, chicken. Green, empirical data; blue, best fit obtained by West et al.¹ (that is, α = 3/4); red, plot of equation (1), with α = 2/3 and the values of M and γ as obtained in ref. 1. d, Scaling collapse. The universal growth curve (equation (2); dotted line) is derived from data from the three species (green, cow; blue, hen; red, guppy) for both α = 3/4 and α = 2/3.

For simplicity, we have chosen M from Table 1 of ref. 1. We determined γ_α = a_α(1−α)/M^1−α using the values of a_3/4 from the same table and a_2/3 for the cow, hen and guppy to be 0.62, 0.67 and 0.064, respectively, to ensure that γ_2/3 = γ_3/4 for simplicity. (We have not tried to adjust the value of M and γ to achieve a better fit because that is beside the point here.) Also, an equally good fit of the universal curve is obtained (Fig. 1d) for the three species with both values of α. Furthermore, the form of the universal curve (equation (2)) is independent of the value of α. Thus, the existence of a universal curve indicates nothing about the value of α.