Introduction

High-energy electrons traveling through matter are highly sensitive to the local structure1, collecting a multitude of information about lattice defects and strain2, electric and magnetic properties3, as well as chemical composition and electronic structure4. This sensitivity is utilized in transmission electron microscopy (TEM) to study structure-property relations, and there are continuous efforts to increase resolution, enhance imaging speeds, and enable new imaging modalities5. A real paradigm shift was triggered by the advent of high dynamic-range direct electron detectors (DED), which no longer rely on converting electrons into photons6,7,8. DEDs enable spatially resolved diffraction imaging, providing additional opportunities for high-resolution measurements known as four-dimensional scanning transmission electron microscopy (4D-STEM)8,9,10. A significant advantage of 4D-STEM is the outstanding information density; an image of the dynamically scattered electrons is acquired at every probe position. In turn, advanced analysis tools are required to deconvolute the rich variety of phenomena that contribute to the scattering of the electrons10,11,12,13. Remarkably, low noise levels on DEDs enable the quantification of weak scattering events (e.g., diffuse scattering due to crystallographic defects14,15). The analysis of 4D-STEM data, however, is often challenged by a lack of empirical models that can fully explain the multitude of dynamic scattering processes, as well as varying signal-to-noise ratios. Recently, exponential increases in the deployment of machine learning methods in microscopy have been applied to accelerate a variety of scientific tasks, including real-time data reduction16, segmentation17,18, and automated experiments19,20. Furthermore, they can be used to disentangle features in multimodal nanoscale spectroscopic imaging with improved statistical significance21,22,23,24. Through careful design of machine learning architectures and custom regularization strategies, it is now possible to statistically disentangle and interpret structural properties of functional materials with nanoscale spatial resolution from multimodal imaging25,26,27.

Here, we apply 4D-STEM to investigate domains, domain walls, and vortex structures in a uniaxial ferroelectric oxide, utilizing the scattering of electrons for simultaneous high-resolution imaging and local structure analysis. Using a convolutional autoencoder (CA) with custom regularization, we statistically disentangle features in the diffraction patterns that correlate with the distinct structural distortions in the ferroelectric domains and domain walls, as well as the domain wall charge state. Based on the specific scattering properties, we can readily gain real-space images of ferroelectric domains, domain walls, and their vortex-like meeting points with a resolution limited by the spot size of the focused electron beam (here, 2 nm). Our approach provides a powerful method that combines nanoscale imaging and structural deconvolution—opening a pathway towards improved structure-property correlations, increased fidelity, and automated scientific experiments.

Results and discussion

Domain wall imaging by scanning electron diffraction

4D-STEM experiments are conducted on a model ferroelectric Er(Mn1-x,Tix)O3 (x = 0.002), denoted Er(Mn,Ti)O3 in the following. The high-quality single crystals used in this study are grown by the pressurized floating-zone method, following the same synthesis procedure as outlined by Yan et al.28. Er(Mn,Ti)O3 is a uniaxial ferroelectric and naturally develops 180° domain walls, where the spontaneous electric polarization P inverts29,30,31,32. The ferroelectric domain walls have a width comparable to the size of the unit cell33, and their basic structural34, electric33,35, and magnetic properties36 are well understood, which makes them an ideal model system for exploring local electron scattering events. It is established that the polarization reorientation across the domain walls coincides with a change in the periodic tilt pattern of the MnO5 bipyramids and displacement of Er ions that drive the electric order (i.e., improper ferroelectricity, see Fig. 1a)31. The structural changes at domain walls alter the electron scattering processes from the bulk. In turn, this difference is expected to alter scattering intensities encoded in the local electron diffraction patterns obtained in scanning electron diffraction (SED) measurements. There are, however, no good analytical methods to disentangle structural and extrinsic (e.g., thickness- and orientation-related) scattering mechanisms, particularly in the presence of noise.

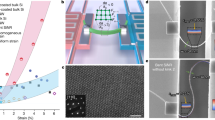
The general working principle of SED measurements is illustrated in Fig. 1b. A focused electron beam is raster-scanned over an electron transparent lamella. The lamella is extracted from an [001]-oriented Er(Mn,Ti)O3 single crystal (P || [001]), using a focused ion beam (FIB) as detailed in Methods. A diffraction pattern is recorded at each probe position of the scanned area, containing information about the local structure. In addition, integrating and selectively filtering the intensities of the collected individual diffraction patterns allows for calculating virtual real-space images. Figure 1c shows such a virtual dark-field (VDF) image. To calculate the VDF, we select and integrate the intensities of the full diffraction patterns as described by Meng and Zuo34. The imaged area contains two ferroelectric 180° domain walls (marked by black dotted lines) that separate +P and −P domains. The polarization direction within the domains was determined before extracting the lamella from the region of interest based on correlated scanning electron microscopy and piezoresponse force microscopy measurements (not shown). A VDF image with a higher resolution is presented in Fig. 1d for one of the domain walls, with visible contrast between the two domains. The data in Fig. 1d is recorded outside the area seen in Fig. 1c to minimize beam exposure (referred to as dataset 1, DS1, in the following).

Fig. 1: Scanning electron diffraction on ferroelectric domains in Er(Mn,Ti)O3.
figure 1

a Crystallographic structure at room temperature (non-centrosymmetric space group P63cm). The Er atoms show a characteristic down-down-up displacement pattern, which correlates with the direction of the spontaneous polarization as illustrated below (down-down-up: −P, up-up-down: +P). b Schematic of our 4D-STEM approach. The illustration shows how the electron beam (green) is scanned across a selected region of a several micrometers sized Er(Mn,Ti)O3 lamella with a domain wall as indicated by the black dashed line, collecting diffraction patterns at a fixed position of the DED. c Overview VDF image showing two ferroelectric domain walls marked by black dashed lines. The bottom part (light gray) is an amorphous carbon layer with Pt markers that were used to cut a lamella from the region of interest. White arrows indicate the polarization direction of the different domains. Scale bar, 250 nm. d High-resolution VDF image recorded at the right domain wall shown in c. Scale bar, 100 nm.

Full size image

Domain-dependent center-of-mass shift

We begin our discussion of the SED results with a center-of-mass (COM) analysis applied to the complete stack of diffraction patterns in the area presented in Fig. 1d. The results of the COM analysis are summarized in Fig. 2a, b. In general, the momentum change of the electron probe can be represented by the orientation of a vector in 2D reciprocal space. When interacting with the sample, the direction of the momentum changes, which is used in 4D-STEM COM imaging to determine built-in electric35 or magnetic37 fields. To evaluate the COM distribution over the dataset, we plot the COM position of each diffraction pattern as a single spot in reciprocal space. The result gained from the whole dataset is shown in Fig. 2a, where a substantial redistribution of scattering intensities is observed along the crystallographic [001]-axis. We find that the COM shift is sensitive to the local polarization orientation in Er(Mn,Ti)O3, leading to a split in the dispersion line for +P (red) and −P (blue) domains, as seen in Fig. 2b. Figure 2b presents the spatial origin of the two contributions, which coincides with the ferroelectric domain structure resolved in the VDF image in Fig. 1d.

Fig. 2: Domain-dependent scattering of electrons.
figure 2

a The center-of-mass (COM) analysis of every diffraction pattern in DS1 shows a substantial shift with respect to the geometric center in the upwards (downwards) direction along the crystallographic [001]-axis for +P (−P) domains. Scale bar, 0.1 Å−1. b COM analysis of the diffraction patterns associated with +P (red) and −P (blue) domains. Scale bar, 100 nm.

Full size image

Convolutional autoencoder analysis of SED data

To analyze the domain-dependent scattering in more detail, we deploy a custom CA. The autoencoder consists of different blocks, as illustrated in Fig. 3a–c. The CA takes the input diffraction patterns and learns a low-dimensional statistical representation of the image through a series of convolutional and residual blocks. In each residual block, a max pooling (MaxPool) layer reduces the dimensionality of the image. Once the dimensionality of the image is sufficiently reduced, the two-dimensional image is flattened into a feature vector. This penultimate bottleneck layer is further compressed to a low-dimensional latent space, where statistical characteristics of the structure are disentangled using a scheduled custom regularizer. The learned latent representation is reshaped into a 2D image and decoded in the decoder using a series of upsampling residual blocks until the image is reconstructed to its original resolution. The model is trained on the diffraction patterns from single STEM images, such that there is a model for each experiment or imaging condition, using momentum-based stochastic gradient descent (ADAM)38 to minimize the mean squared reconstruction error of the diffraction images and regularization constraints added to the loss function.

Fig. 3: Structure of the custom CA.
figure 3

a Main structure, consisting of encoder (from input to flatten layer), embedding, and decoder (from dense layer to reconstruction). The encoder reduces the dimension of each input image by going from 256 × 256 pixels to 8 × 8 pixels and via a dense layer down to the embedding. The embedding controls the number of channels to generate individual domains and domain walls in real space. The decoder recreates the vector from the embedding to the input image size. b Detailed structure of the ResNet MaxPool Block. The block consists of four convolutional layers, two normalization layers, two ReLU activation layers, and one 2D MaxPool layer with shortcut. c Detailed structure of the ResNet UpSample Block. The block contains one 2D upsample layer, four convolutional layers, two normalization layers, and two ReLU activation layers with shortcut. d Averaged diffraction pattern of a +P domain in dataset DS1, corresponding to the left domain (orange) seen in the CA embedding in the inset. e Averaged diffraction pattern of the −P domain (purple) in the CA embedding in the inset to d.

Full size image

The overarching objective in learning latent representations is to isolate the salient statistical attributes embedded within the data. Traditional β-Variational Autoencoders (VAEs)39,40,41 accomplish this by imposing penalties on non-Gaussian features within the latent space—a very useful characteristic for generative models. This foundational principle has been adapted to allow for the soft disentanglement of geometric transformations, such as rotation, translation, strain, and shear42,43. However, the assumption of a Gaussian-distributed latent space introduces constraints, specifically excluding non-negativity and sparsity—properties that bolster interpretability. Additionally, this Gaussian assumption enforces an unphysical prior when attempting to identify intrinsically non-Gaussian features, like domain walls (Supplementary Fig. 1).

We impose various constraints on the embedding layer to encourage interpretable disentanglement of ferroelectric domains in the latent space. First, we add a rectified linear activation (ReLU) to ensure the activations are non-negative. All neural networks have a loss function based on the mean squared reconstruction error \({MSE}\left(y,\hat{y}\right)=\frac{1}{D}{\sum }_{i=1}^{D}{\left({y}_{i}-{\hat{y}}_{i}\right)}^{2}\), where \(y\) and \(\hat{y}\) denote the \(D\)-dimensional output and input of the neural network (D = 2562 = 65,536), respectively. To impose sparsity (a limited number of activated channels), an additional activity regularization is introduced \({L}_{1}\left(a\right)={\sum }_{i=1}^{d}\left|{a}_{i}\right|\), leading to a total loss function

$$L={MSE}\left(y,\hat{y}\right)+{\lambda }_{\text{act}}{L}_{1}\left(a\right);$$
(1)

here, d is the dimensionality of the embedding layer, \({a}_{i}\) are the activations in the embedding layer, and \({\lambda }_{\text{act}}\) is a hyperparameter. This has the effect of trying to drive most activations to zero while only those essential to the learning process are non-zero. As the degree of sparsity required is dataset-dependent, regularization scheduling is used to tune \({\lambda }_{\text{act}}\) to achieve an interpretable degree of disentanglement.

To demonstrate the efficiency of the CA, we analyze 4D-STEM data from the region with two ferroelectric domains seen in Fig. 1d (DS1). The model is trained with an overcomplete embedding layer of size 32. Following training, the number of active channels is reduced to 9 (see Supplementary Note 1 and Supplementary Fig. 2). Most of the embeddings disentangle bias in the imaging mode associated with the scan geometry, varying specimen thickness and orientation variations due to specimen bending; additionally, features associated with the domain wall are disentangled, which we will discuss later. One channel shows a sharp contrast between the 180° domains, indicating a significant contrast mechanism (inset to Fig. 3d). This map represents the activations of one neuron and, hence, is a weighting map for a specific characteristic in the diffraction pattern. To elucidate the nature of the contrast mechanism, we traverse the neural network latent. We show the generated diffraction patterns from the latent space encompassing the +P and −P domains in Fig. 3d, e.

The CA analysis reveals variations between the two domain states in the scanned area for the strongest reflections along the [001]-axis, that is, the \(004\) and \(00\bar{4}\) reflections (note that intensity distributions vary with sample thickness). A substantial advantage of the CA-based approach compared to, e.g., signal decomposition via unsupervised non-negative matrix factorization, is that it does not create artificial components that resemble diffraction patterns. Instead, the CA rates each diffraction pattern according to the scattering features in the embedding channels. Thus, by selecting and averaging diffraction patterns within a specific activation range within a certain channel, one can readily use this approach as a virtual aperture in reciprocal space using multiple areas of the pattern to correlate structural features identified statistically to scattering properties.

To demonstrate that the diffraction patterns in Fig. 3d, e are indeed specific to the local polarization orientation and connect them to the atomic-scale structure of Er(Mn,Ti)O3, we simulate the diffraction patterns expected for +P and −P domains using a Python multislice code44. As one example, Fig. 4a displays the unit cell structure of a +P domain, which is reflected by the up-up-down pattern formed by the Er atoms45. The corresponding simulated diffraction pattern is presented in Fig. 4b, considering a sample thickness of 75 nm. Figure 4b shows an asymmetry in the 004 and \(00\bar{4}\) reflections, consistent with the diffraction data in Fig. 3d. For a more systematic comparison of the experimental and simulated diffraction patterns, we calculate the normalized cross-correlation Δ(+P, −P) between the patterns of the two domains, as shown in Fig. 4c (simulated) and Fig. 4d (experimental data DS1). In both cases, the variational maps show the highest intensities wherever the two compared patterns exhibit the strongest variations. As expected, those arise primarily in the 004 (\(00\bar{4}\)) and, less pronounced, in the 002 (\(00\bar{2}\)) reflections. This observation further corroborates the CA-based analysis of the SED data, linking the changes in the diffraction pattern intensities to the atomic displacements and the resulting polarization direction.

Fig. 4: Comparison of measured and simulated SED diffraction patterns.
figure 4

a Illustration of the atomic structure in +P domains, showing the characteristic up-up-down displacement pattern of Er atoms. The crystallographic [001] and [010] axes are indicated by the inserted coordinate systems. b Simulated diffraction pattern for the structure in a. The direct beam and the 004 and \(00\bar{4}\) reflections are marked by white circles. c Normalized cross-correlation between simulated and d experimental (DS1) diffraction patterns of −P and +P domains, Δ(+P, −P), showing that the highest variation occurs for the 004-reflection.

Full size image

CA-based extraction of domain walls and vortices

After demonstrating that our approach is sensitive to the polar distortions in Er(Mn,Ti)O3, and that it can extract domains, we discuss local variations in the diffraction pattern intensities that originate from finer structural changes. Figure 5a displays the same embedding map as seen in the inset to Fig. 3d, showing two ferroelectric domains with opposite polarization orientation. A second embedding map is shown in Fig. 5b, indicating scattering variations at the position of the domain wall (see also Supplementary Note 1 and Supplementary Fig. 2). The latter reflects the broader applicability of the CA beyond domain-related investigations. To explore the possibility of investigating local structure variations also at domain walls, we conduct additional measurements on a sample with multiple walls that meet in a characteristic six-fold meeting point, leading to a structural vortex pattern30,33,36 as presented in Fig. 5c–f (referred to as DS2). It is established that such vortices promote the stabilization of different types of walls46, which allows for testing the feasibility of our 4D-STEM approach for structure analysis of ferroelectric domain walls with varying physical properties.

Fig. 5: Domains and domain walls extracted via the CA.
figure 5

a Embedding map showing ferroelectric ±P domains (DS1). Scale bar, 75 nm. Polarization directions are given by white arrows (same as inset to Fig. 2c). b Embedding map revealing the domain wall that separates the domains in a. c Embedding map from a second sample (DS2). Scale bar, 90 nm. d Difference in diffraction patterns between +P and −P domains in (c). e, f Two embedding maps of the CA, separating head-to-head (e) and tail-to-tail (f) domain walls that belong to the vortex in c.

Full size image

As the statistics of the domain walls are different than within the domains, a uniform sparsity metric cannot disentangle these features well. Thus, to improve the performance of our model, we add two additional regularization parameters to the loss function that encourage sparsity and disentanglement. First, we add a contrastive similarity regularization of the embedding, \({L}_{{\rm{sim}}}\), to the loss function. This regularization term computes the cosine similarity between each of the non-zero vectors \({a}_{i}\) and \({a}_{j}\) within a batch of embedding vectors, where \({N}_{{\rm{batch}}}\) is the batch size, and \({\lambda }_{{\rm{sim}}}\) is a hyperparameter that sets the relative contribution to the loss function:

$${L}_{{\rm{sim}}}=\frac{{\lambda }_{{\rm{sim}}}}{2{N}_{{\rm{batch}}}}\mathop{\sum }\limits_{i=1}^{{N}_{{\rm{batch}}}}\left(\left[\mathop{\sum }\limits_{j=1}^{{N}_{{\rm{batch}}}}\frac{{a}_{i}\cdot{a}_{j}}{{\rm{||}}{a}_{i}{\rm{||}}\cdot {\rm{||}}{a}_{j}{\rm{||}}}\right]-1\right).$$

Since the activations are non-negative, the cosine similarity is bounded between [0,1], where 0 defines orthogonal vectors, and 1 defines parallel vectors. We subtract 1, so that similar and sparse vectors have no contribution to the loss function, whereas dissimilarity of non-sparse vectors decreases the loss and, thus, is encouraged.

Secondly, we add an activation divergence regularization, \({L}_{{\rm{div}}}\), to the loss function, where \({a}_{i,j}\), \({a}_{i,k}\) are components of the ith vector within a batch of latent embeddings. The magnitude of this contribution is regulated using the hyperparameter \({\lambda }_{{\rm{div}}}\):

$${L}_{{\rm{div}}}=\frac{{\lambda }_{{\rm{div}}}}{2{N}_{{\rm{batch}}}}\mathop{\sum }\limits_{i=1}^{{N}_{{\rm{batch}}}}\left(\mathop{\sum }\limits_{j=1}^{d}\mathop{\sum }\limits_{k=1}^{d}\left|{a}_{i,j}-{a}_{i,k}\right|\right).$$

This term has the effect of enforcing that each embedding vector is sparse, having a dominate component that is easy to interpret. We use the hyperparameter \({\lambda }_{\text{div}}\) to ensure that the magnitude of this contribution is significantly less than the reconstruction error. When applying these custom regularization strategies, the resulting activations disentangle more nuanced features in the domain structure.

The model readily disentangles the +P and −P domain states, as presented in Fig. 5c, revealing a six-fold meeting point of alternating ±P domains. The difference pattern between the two domain states can be determined using the CA as a generator. To do so, we calculate the mean pattern of the upper 5% quantile of the +P (purple) and −P (orange) domains in Fig. 5c, which leads us to Fig. 5d (corresponding color histograms are shown in Supplementary Fig. 3). Consistent with Fig. 4, pronounced intensity variations between +P and −P domains are observed for the 004 (\(00\bar{4}\)) and 002 (\(00\bar{2}\)) reflections. In contrast to the data collected on the first sample (Fig. 4), however, Fig. 5d reveals a stronger variation in the 002 (\(00\bar{2}\)) reflections, which we attribute to a difference in sample thickness.

Interestingly, the neural network produces different embedding maps for the domain walls in Fig. 5c, indicating a difference in their scattering behavior. Specifically, we disentangle statistical features that reveal the existence of two sets of domain walls as shown in Fig. 5e, f, respectively (additional embeddings are shown in Supplementary Fig. 3). Based on the polarization direction in the adjacent domains, we can identify the two sets of domain walls as positively charged head-to-head walls (Fig. 5e) and negatively charged tail-to-tail walls (Fig. 5f). This separation regarding the polarization configuration is remarkable as it reflects that our approach is sensitive to both the crystallographic structure of the domain walls and their electronic charge state as defined by the domain wall bound charge33.

In summary, our work demonstrates a powerful pathway for imaging and characterizing ferroelectric materials at the nanoscale. By applying a custom-designed CA to SED data gained on the model system Er(Mn,Ti)O3, we have shown that different scattering signatures can be separated within the same experiment. The latter includes ferroelectric domains, domain walls, and emergent vortex structures, as well as extrinsic features (e.g., bending and thickness variations), giving access to both the local structure and electrostatics. Analogous to the training specifically performed for the Er(Mn,Ti)O3 datasets, the model can be trained and specifically tailored to other systems. The core elements of the model—including its architecture, regularization techniques, and hyperparameters tuning methods—are broadly applicable to high-dimensional imaging modalities, not only in ferroelectrics. Thus, the findings can readily be expanded to other systems to localize, identify, and correlate weak scattering signatures to structural variations based on SED. By building a CA with custom regularization to promote disentanglement, subtle spectroscopic signatures of structural distortions can be statistically unraveled with nanoscale spatial precision. This approach is promising to automate and accelerate the unbiased discovery of defects, secondary phases, boundaries, and other structural distortions that underpin functional materials. Furthermore, it opens the possibility to expand the design of experiments to larger imaging sizes, higher frame rates, and more broadly into automated experimentation and, eventually, controls.

Methods

Specimen preparation

The lamellas used in this work are extracted from an Er(Mn,Ti)O3 single crystal using a FIB. For this purpose, the crystal is first oriented by Laue diffraction and cut perpendicular to the polar axis (P || [001]), to achieve a sample with out-of-plane polarization (thickness ~1 mm). To confirm that the crystal exhibits the characteristic domain structure of the hexagonal manganites, it is chemo-mechanically polished with silica slurry, which gives a root-mean-square roughness of about 1 nm and allows for domain imaging by, e.g., piezoresponse force microscopy and scanning electron microscopy (SEM) (not shown, for an example, see Evans et al.47). From the pre-characterized sample, a smaller piece is cut with a lateral dimension of about 2 × 2 mm2 for the FIB preparation48. This sample is then mounted on an SEM specimen holder with carbon tape and loaded into a Thermo Fisher Scientific G4 UX DualBeam FIB. This system combines a SEM and a gallium (Ga) ion beam column. The region of interest (ROI) is located by SEM imaging and platinum markers, and a carbon protection layer is deposited by the electron beam. This step is critical as it ensures that the ROI is marked and shielded from any potential ion beam irradiation damage. Subsequently, another carbon protection layer is deposited by the ion beam. Following the deposition steps, a Ga ion beam is used to mill trenches on each side of the ROI, after which the lamella is extracted and transferred to a copper TEM grid. The lamella is then progressively thinned down towards the pre-marked target position with the ion beam, with the current gradually decreasing from 9 nA to 90 pA. This thinning process ends with a lamella where the ROI is located in the upper middle of the lamella, with the ROI thinner than the surrounding areas to ensure optimal flatness. The process is stopped as the ROI becomes electron transparent49. For the final polishing step, a low-energy electron beam (2 kV, 0.11 nA) is used to remove the damage layer50 and improve the surface quality.

Diffraction data acquisition and STEM imaging

The diffraction experiments were conducted on a Jeol 2100 F TEM at 200 kV and the scans were controlled via the Nanomegas P1000 scan engine. For acquiring the diffraction patterns, we used a Merlin 1S DED from Quantum Detectors operated with a lower threshold of 40 kV and with no limit on the upper threshold. The electron beam is focused on a probe with a diameter of 2 nm and a convergence angle of 9 mrad. The total scan grid consisted of 256 × 256 probe positions (with a step size of 1.4 nm) with a probe dwell time of 50 ms at each beam position. STEM imaging was performed using the nanobeam diffraction mode and a 10 µm aperture. The probe current was measured to be 4.6 pA.

Convolutional autoencoder (CA)

Data from 4D-STEM was analyzed using a CA built in Pytorch51. Prior to training, the log of the raw 4D-STEM data was used to obtain less non-linear images. The number of learnable parameters is 4,700,770. The CA consists of three parts: an encoder, an embedding layer, and a decoder. The encoder consists of three ResNet Blocks with different feature sizes, a convolutional layer with one filter, and a flattened layer. Each ResNet Block consists of a Residual Convolutional Block and an Identity Block. Each Residual Convolutional Block has three sequence convolutional layers with 128 filters, connected with a normalization layer and a Rectified Linear Unit (ReLU) activation layer. There is a skip connection between the input and output of the block, which can maintain the information of the input image after image processing. Each Identity Block has a convolutional layer with 128 filters, connected with a normalization layer and a ReLU activation layer. There is a 2D Max Pooling layer after each Resnet Block for image size dimensionality reduction. The image sizes to each ResNet Block in the encoder are (256 × 256), (64 × 64), (16 × 16). The embedding consists of a linear layer and a ReLU activation layer. The decoder consists of a linear layer, a convolutional layer with 128 filters, three ResNet Blocks, and a convolutional layer with 1 filter. There is an upsampling layer before each ResNet Block to recreate the input image. A loss function based on the mean square reconstruction error (MSE) between the input and generated image is used. The image sizes to each ResNet Block in the decoder are (8 × 8), (16 × 16), (64 × 64). The loss function has additional L1 activity regularization of the embedding. When generating domain walls in Fig. 5e, f, we also include contrastive similarity regularization and activate divergence regularization to make the output embedding sparse and unique.

The models were trained on a server with 4x A100 GPUs. To generate the domain in Fig. 5a and the domain wall in Fig. 5b, we set the coefficient \({\lambda }_{\text{act}}=1\times {10}^{-5}\) and trained the model using optimization ADAM52 (learning rate of 3 × 10−5) for 377 epochs. To generate the vortex-like domain pattern (Fig. 5c), we set the coefficient \({\lambda }_{\text{act}}=1\times {10}^{-5}\) and trained the model for 225 epochs using optimization ADAM (learning rate of 3 \(\times {10}^{-5}\)), then raised \({\lambda }_{\text{act}}\) to \(5\times {10}^{-4}\) and trained the model for another 60 epochs using learning rate cycling (increasing from 3\(\times {10}^{-5}\) to 5\(\times {10}^{-5}\) in 15 epochs, then decreasing from 5\(\times {10}^{-5}\) to 3\(\times {10}^{-5}\) in the next 15 epochs). To generate the corresponding domain walls in Fig. 5e, f, besides L1 regularization with coefficient \({\lambda }_{\text{act}}=5\times {10}^{-3}\) in the loss function, we also included contrastive similarity regularization with coefficient \({\lambda }_{\text{sim}}=5\times {10}^{-5}\) and activity divergence regularization with coefficient \({\lambda }_{\text{div}}=2\times {10}^{-4}\) to make the output embedding sparse and unique. We trained the model for 18 epochs using optimization ADAM (learning rate of 3\(\times {10}^{-5}\)). Following training, the output from the embedding layer was extracted. This represents a compact representation of the important features in the sample domain. To visualize the change in the diffraction pattern that is encoded by a single channel, the difference between the mean pattern of all diffraction pattern with 5% highest and lowest activation at the channel of interest was calculated. This was used to create the projections in Figs. 3d, e, 4d, 5d and the third row of Supplementary Fig. 3. Full details are available in the reproducible source code38.