Introduction

Optical microscopy has been a fundamental tool for biological discovery and an increasingly important tool for studying the development, progression and potential treatment of pathological conditions such as tumors and neurodisorders1,2. Conventional optical microscopy, however, has been limited to tissue samples (10–20 μm thickness) due to light scattering. Confocal microscopy can image tissue at a depth of up to several mean free paths (MFP) of a photon (1 MFP≈100 μm in tissue) by using a detection pinhole to reject photons that reach the detector from out of focus planes. Two- or multi-photon (2P/MP) microscopy can achieve 2–3 times deeper penetration than confocal microscopy due to the use of two- or multi- photon absorption in the near-infrared region2,3. Optical coherence tomography (OCT) excites tissue with low coherence light and detects back reflected light based on coherence matching between the incident and reflected light beams using an interferometric approach4. While confocal and 2P/MP microscopy and OCT are capable of in vivo imaging, optical scattering prevents these methods from imaging deeper than ~1 mm below the tissue surface. Further, all these methods do not directly sense optical absorption, a property strongly associated with the functional/physiological status of tissue since confocal and 2P/MP microscopy generally image fluorescent proteins/dyes and OCT detects primarily structures that scatter light.

Photoacoustic microscopy (PAM) is an emerging powerful approach for imaging optical absorption5. PAM detects absorbed photons ultrasonically through the photoacoustic effect. Since ultrasonic scattering is 2 to 3 orders of magnitude weaker than optical scattering in tissue, PAM breaks the ~1 mm depth limit associated with confocal and 2P/MP microscopy and OCT. In PAM, tissue is excited with a short (a few nanoseconds) laser pulse (focused or unfocused) and the laser-induced transient photoacoustic waves in the range of 1–100 MHz, due to the transient thermoelastic expansion of light-absorbing structures, are detected by a wideband focused ultrasound transducer. The time-resolved photoacoustic waves recorded at each location of the transducer are then converted into a one-dimensional (1D) depth-resolved image (A-scan) assuming a constant acoustic speed in tissue. Raster scanning the laser beam and transducer along a horizontal plane produces a three-dimensional (3D) image. PAM has been shown so far to be particularly useful for imaging microvasculature associated with neural activity and tumors and for detecting optical reporters in high resolution6,7.

PAM, however, is essentially qualitative in nature since it measures the absorbed optical energy density, the product of the absorption coefficient and the local optical fluence rather than the absorption coefficient itself. This prevents PAM from quantitatively measuring important functional parameters including oxyhemoglobin (HbO2), deoxyhemoglobin (HbR) and oxygen saturation (sO2). Absolute quantification of these functional parameters will allow for correct determination of the physiological status of tissue and accurate diagnosis of pathological conditions such as tumors and neurodisorders. While almost all the existing PAM methods5,8,9,10,11,12,13 can measure only relative or semi-quantitative concentration of HbR and HbO2, initial effort has been made to quantify optical absorption coefficient using acoustic spectra in PAM14,15. However, in this initial effort a non-model-based technique was used where the optical fluence was assumed as uniformly distributed across the target/object and background media, making it inevitable to negatively affect the accuracy of quantifying absorption coefficient through a fitting optimization approach. Therefore, there is a clear need of developing new model-based PAM methods to provide truly accurate photoacoustic imaging.

We have developed a new photoacoustic microscopy method, which we term, photoacoustic computed microscopy (PACM), to address this critical need. Central to PACM is a model-based inverse reconstruction algorithm, which uses the photoacoustic signals measured by a focused transducer to obtain quantitative images of HbO2, HbR and sO2. In addition, assisted with an oxygen-transport model PACM permits determination of two other important functional parameters, blood flow (BF) and rate of oxygen metabolism (MRO2). These two parameters currently are available from some imaging techniques, such as positron emission tomography (PET), single photon emission computed tomography (SPECT), computed tomography (CT) with a contrast agent, magnetic resonance imaging (MRI), Xenon clearance and diffuse correlation spectroscopy (DCS). Compared to these techniques, PACM has the potential to be a viable candidate for visualizing microvasculature dynamics with high spatial resolution at relatively much lower cost.

Results

The PACM reconstruction algorithm (see the Method section) is first tested using six sets of tissue-mimicking phantoms with known optical properties (Table 1). Fig. 1(a)–(f) shows the reconstructed absorption coefficient images from these phantom experiments. We see that the object(s) in each case are clearly detected by our PACM approach. In particular, these images are quantitatively accurate in terms of the absorption coefficient of target. This conclusion is further confirmed by the quantitative absorption coefficient profiles for these images provided in Fig. 1(g)–(h). We found that the relative error of the recovered absorption coefficient of target compared to the exact value is less than 4.7% for the single target cases 1–5, while it ranges from 2.8% to 9.5% for the multi-target case 6 (Table 1). We note that the target having higher contrast (cases 1–3) is better reconstructed than for the lower contrast cases (case 4).

Table 1 Exact and recovered size and absorption coefficient value of target for the phantom experiments
Full size table
Figure 1
figure 1

Reconstructed absorption coefficient images from the phantom experiments.

(a) Case 1. (b) Case 2. (c) Case 3. (d) Case 4. (e) Case 5. (f) Case 6. (g) & (h) Quantitative plots: reconstructed absorption coefficient profiles along y = 0.0 mm for case 1, y = −4.8 mm for case 2, y = −7.6 mm for case 3, y = −2.1 mm for case 4, y = −1.1 mm for case 5 and y = −1.9 mm for case 6.

Full size image

A rat ear experiment was chosen to further evaluate the algorithm and show its possible application to functional imaging based on physiologically specific endogenous optical absorption contrasts in biological tissue. In Fig. 2(a) we present the maximum amplitude projection (MAP) images projected along the vertical direction (z axis) to the orthogonal plane where seven orders of vessel branching, indicated by numbers 1–7, can be observed in the image. The B-scan image and the reconstructed absorption coefficient image obtained by our FE-based PACM algorithm are shown in Figs. 2(b) and 2(c), respectively. These images are in the vertical plane (x-z plane) at the location indicated by the dash line in Fig. 2(a). It can be clearly seen that all of the vessel branching can be reconstructed using both the methods. The laser applied in this experiment was at a wavelength of 532 nm and from Fig. 2(c) we found that at most locations within the blood vessel, the value of the reconstructed absorption coefficient is in the range of 20 ~ 30 mm−1, which is in good agreement with that of blood vessels at 532 nm reported in the literature16,17.

Figure 2
figure 2

in vivo imaging of the blood vessels in a rat ear.

(a) the MAP image of the photoacoustic signals projected on the orthogonal plane, with seven small vessels that can be observed in the image as indicated by numbers 1–7; (b) B-scan image in the vertical plane at the location indicated by the dash line in (a); (c) reconstructed absorption coefficient image in the vertical plane at the location indicated by the dash line in (a).

Full size image

We then demonstrate PACM's ability of in vivo imaging HbO2, HbR, sO2, cerebral blood flow (CBF) and cerebral rate of oxygen metabolism (CMRO2) using a rodent model in non-diseased condition. Fig. 3(b) shows a typical in vivo B-scan PAM image of a single blood vessel located 1.5 mm below the surface of the rat brain with intact skull (along y-z plane) at a selected time point, which was taken at the location indicated by the dashed line (Fig. 3(a)) (a total of 10 B-scan images were obtained over 60 s duration). EEG signal from one electrode is given in Fig. 3(c). For simplicity, the reconstructions of quantitative absorption coefficient and all the hemodynamic response parameters were conducted over the square area shown in Fig. 3(b). Using the PACM reconstruction algorithm, we obtained the absorption coefficient images at 730 and 1064 nm over 60 s duration and Figs. 4(a)–4(h) show the absorption coefficient images for the two wavelengths at four selected time points, t1 = 12 s, t2 = 24 s, t3 = 42 s and t4 = 54 s. These high-resolution images not only allow for the accurate recovery of the size/shape/location of single blood vessel, but the absolute absorption coefficient itself (indicated by the color scale on right). The absorption coefficient images at 730 and 1064 nm allowed us to obtain HbO2 (Figs. 5 (a)–5(d)), HbR (Figs. 5(e)–5(h)) and sO2 (Figs. 5(i)–5(l)) using Eq. (4) (see the Method section) at the four selected time points as well as at other time points. It can be seen that these functional parameters can also be reconstructed quantitatively over time. To closely observe dynamic evolvement of the functional parameters including HbO2, HbR and sO2, we calculated the average value of these parameters over 60 s time course in a region of interest (ROI), depicted by a 0.1 mm-diameter circle shown in Fig. 5(b) and the results are presented in Figs. 7(b), 7(c) and 7(d). Based on these results, the reconstructed CBF and CMRO2 images at four different times are provided in Figs. 6(a)–6(d) and 6(e)–6(h). The average values of CBF and CMRO2 in the ROI over the 60 s time course are shown in Figs. 7(e) and 7(f).

Figure 3
figure 3

(a) Photograph of the rat brain with intact skull under PAM imaging. The arrow/dashed line indicates the B-scan path for PAM. (b) Typical B-scan PAM image. Note that the blood vessel imaged is ~1.5 mm below the surface. (c) EEG signal recorded at one electrode close to the scanned region.

Full size image
Figure 4
figure 4

Reconstructed absorption coefficient images using the in vivo rodent model.

a–d: 730 nm; e–h: 1064 nm at four different time points (a & e: t = 12 s; b & f: t = 24 s; c & g: t = 42 s; d & h: t = 54 s).

Full size image
Figure 5
figure 5

Reconstructed functional images using the in vivo rodent model.

a–d: HbO2, e–h: 1 HbR and i–l: sO2 at four different time points (a, e & i: t = 12 s; b, f & j: t = 24 s; c, g & k: t = 42 s; d, h & l: t = 54 s).

Full size image
Figure 6
figure 6

Reconstructed CBF (a–d) and CMRO2 (e–h) images at t = 12 s (a,e), 24 s (b,f), t = 42 s (c,g) and t = 54 s (d,h).

In the calculation, the initial parameters used were: [HbT]blood = 0.72 mM, f = 0.2 and = 0.98 (see the Method section for the explanation of these initial parameters). In addition, due to the high nonlinear distribution of sO2 over time, the sO2 distribution curve was first separated into several approximated linear segments to improve the fitting accuracy of CBF and CMRO2. The mean CBF and CMRO2 were fitted for each linear segment based on different initial values of [HbT] and sO2.

Full size image
Figure 7
figure 7

Comparison of the EEG signal and the average values of the recovered functional parameters of the ROI during the entire time course.

(a) Filtered EEG signals; (b) average HbO2 of the ROI; (c) average HbR of the ROI; (d) average sO2 of the ROI; (e) average CBF of the ROI; (f) average CMRO2 of the ROI.

Full size image

Discussion

The reconstructed results of optical absorption coefficient obtained from the phantom experiments and the rat ear are both qualitatively and quantitatively in terms of the location, size, shape and optical property values of the target and background, which indicates that the PACM method has the capability to provide absolute functional imaging based on physiologically specific endogenous optical absorption coefficient. This capability is confirmed with an animal experiment by using a rodent model (see the Result section), but in principle any animal model associated with neural activation/stimulation could be used.

In this study we first obtained the reconstructed absorption coefficient images at two wavelengths (730 nm and 1064 nm) at four different points (12 s, 24 s, 42 s and 54 s) as shown in Fig. 4. Functional information including HbO2, HbR and sO2 at these time points are presented in Fig. 5. We note that the total hemoglobin concentration ([HbT] = [HbO2] + [HbR]) of the blood vessel is in the range of 40–50 g/l, which agrees well with that described in the literature18. The dynamic changes of these functional parameters in the ROI are also clearly notable in Figs. 7(b)–7(d). Inspecting the filtered EEG signal over time (Fig. 7(a)), we find that two significant spikes at 20 s and 50 s in the EEG signals can also be identified in Figs. 7(b) and 7(c).

Using Eqs. (6) and (7) (see the Method section), we have also calculated CBF and CMRO2 over the total time course. We can observe significant changes in CBF and CMRO2 in terms of the shape/size of blood vessel and values of CBF/CMRO2. We also see from the peak values of CBF shown in Fig. 6 that the recovered blood flow values (7.5–8.5 ml/ml/s, or 45–51 ml/100 ml/min) are in good agreement with the reported CBF of rats (10–120 ml/100 ml/min) and of humans (20–160 ml/100 ml/min)19,20. Average values of CBF and CMRO2 in the ROI are provided in Figs. 7(e) and 7(f). Interestingly, CBF and CMRO2 spikes stronger in intensity than that seen in HbR and HbO2 are clearly notable.

While it is a novel approach to monitor the dynamic response of functional parameters quantitatively, PACM presented here has some limitations and needs to be improved in the future. In this study, we estimated a homogenous distribution of scattering coefficient in advance when the absorption coefficient was recovered. For the animal experiments the reduced scattering coefficient was assumed as 1.0/mm. It is well known that the propagation of light in turbid media is strongly characterized by optical absorption and scattering; thus this approximation would introduce a negative impact on the accuracy of the recovery of absorption coefficient. This impact, however, was small since the contribution of scattering to the photoacoustic data is much less than that of absorption, if the estimated distribution of scattering coefficient is in a reasonable range. For example, based on our numerical simulations, when the estimated error of the reduced scattering coefficient is within the range of ±50% of the actual value, the error of the recovered absorption coefficient is less than 5%. Recovering absorption and scattering coefficients simultaneously will improve the accuracy of the reconstructed results, but it will suffer from strong nonuniqueness for such inversion of multiple parameters. In this study, since we focus on introducing a new method exploiting the recovery of absorption coefficient and other associated parameters of biological tissue, this approximation for scattering coefficient was used for simplicity. We plan to develop methods for minimizing the impact of scattering on the recovery of absorption coefficient in the future.

To produce the functional parameters in the blood vessel by PAM, laser beams at 730 nm and 1064 nm were used in this study due to the limitation of our current hardware. The contribution of water to the absorption coefficient should be considered, since the molar extinction coefficient of water at the wavelength 1064 nm cannot be ignored compared to that of the oxygenated and deoxygenated hemoglobin. In this study, we made an assumption that ratio of the concentration of water to the total hemoglobin in blood was about 80%:20%, based on the fact that blood is composed of 80.6% water38. Dynamic images (i.e., BF and MRO2) with similar values as the ones obtained under the assumption were obtained if different ratios other than 80% were used in the calculations. In future studies, we will better consider the impact of water by using laser beams at three different wavelengths, or at two wavelengths (for example, 730 nm and 850 nm), at which the molar extinction coefficient of water is relatively low.

The model we used to calculate BF and MRO2 in blood vessels from the functional parameters is based on the principle of mass balance to the transport of oxygen in a blood vessel segment. Some assumptions are made in order to use this model. For example, oxygen consumption and blood flow are assumed constant during the measurements, due to the need for a sufficient time interval to obtain stable fitting results. While this is a very good assumption for oxygen consumption, blood flow may change during tissue relaxation, indicating that the fitted blood flow value represents a measure of an average blood flow during the measurement period. The accuracy of the fitting results can be improved by increasing the temporal resolution of our imaging system.

In our calculations we assumed [HbT]blood = 0.72 mM, f = 0.2, sO2,ti = 0.98. The values of sO2,ti and f were taken from the literatures21,22. With respect to the choice of [HbT]blood, the normal hemoglobin concentration is in the range of 120–160 g/L for females18 and since the hematocrit values of the capillary vessels is known to be 2–5 times lower than the systemic hematocrit23. For the purposes of this study, we assumed a value of 140 g/L for systemic hemoglobin concentration and a 3 times dilution factor in the small blood vessels, resulting in a value of 0.72 mM for [HbT]blood. We note that the choice of [HbT]blood does influence the flow results, but it does not affect the calculated oxygen consumption, because the inflow and outflow terms appear as part of a product with [HbT]blood in the mass balance equations.

In summary, we have demonstrated that PACM is capable of in vivo imaging a full set of functional parameters at the small vessel level. The dynamic changes are comparable with concurrently recorded EEG signals. The spatial resolution of PACM is the same as PAM, scalable with the central frequency of the focused transducer, i.e., higher resolution at the single cell level is achievable with the sacrifice of penetration depth. The imaging speed of the current PACM is relatively slow (6 s), but it can be improved considerably by using faster lasers. We expect PACM will be a valuable tool for neuroscience research where hemodynamics associated with microvasculature in response to neural activation/stimulation need to be imaged. PACM will also be applicable to visualize microvasculature dynamics involved in tumor angiogenesis and in inflammatory joint diseases.

Methods

PAM imaging system

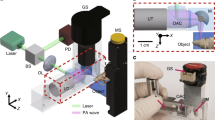
The PAM imaging system is schematically shown in Fig. 8(a). Short-pulsed laser beam at 10 Hz repetition rate from a Nd:YAG laser and/or a Ti:Sapphire laser can be used for imaging. The laser beam from each laser is delivered to the sample via an optic fiber bundle. Both the optic fiber bundles are positioned to produce an optimal illumination at the sample surface as shown in Fig. 8(b). Depending on the application, either one of the lasers or both of them are used for multispectral imaging (e.g., 1064 nm from Nd:YAG and 730 nm from Ti:Sapphire) where a 50-μs time delay between the two lasers provided by the function generator is used to avoid signal overlap. The imaging probe consisting of a focused transducer and the optic fiber bundles is mounted on a two-dimensional (2D) moving stage. The sample is positioned under an open imaging window at the bottom of the water tank sealed with an ultrasonically and optically transparent membrane. Ultrasound gel is used between the membrane and the animal tissue/phantom for acoustic transmission. At each imaging probe position, the laser-induced photoacoustic signal is received by the transducer, amplified by the amplifier and digitalized by a 8-bit data acquisition board (NI5152, National Instrument) at a sample rate of 250 MS/s. One- or two-dimensional raster scanning of the imaging probe along the horizontal plane coupled with the depth-resolved ultrasonic detection forms a 2D or 3D photoacoustic image. It takes ~6 s for a typical B-scan 2D imaging. For the phantom experiments, a focused transducer with 3.5 MHz central frequency, 15 mm aperture and 35 mm focal length was used, which yields a lateral resolution of 800 μm and an axial resolution of 200 μm. For the in vivo animal experiments, a focused high-frequency transducer (50 MHz, 3 mm aperture and 6 mm focal length) was used, which provides a lateral resolution of 61 μm on the focal point and an axial resolution of 15 μm.

Figure 8
figure 8

(a) Schematic of the PAM system. (b) Top view illustration of the optical illumination area. (Created by L.X.)

Full size image

Phantom experiments

For these experiments, laser pulses at 730 nm from the Ti:Sapphire laser were used to image one 0.8 mm-diamter circular target (for cases 1–5) or three circular targets (0.8 mm in diameter each) (for case 6) embedded in the background, which was a scattering medium composed of a fat emulsion suspension (Intralipid) with India ink added as an absorber. The method we used to determine the absorption and reduced scattering coefficients of the phantoms in this study has been widely adopted in the field of diffuse optical imaging and spectroscopy24,25,26,27,28. The absorption of the suspension is essentially due to water for wavelengths between 600 and 850 nm25,26, hence the ink provided a controlled way of achieving a higher level of absorption27. It is also known that the added ink should not have a significant impact on the scattering coefficient27. The targets were transparent tube containing different concentrations of Intralipid and India ink which were used to simulate heterogeneities. For example, based on the recipe for using India ink as absorber and Intralipid as scatterer and the formula to calculate absorption and scattering coefficients27,28, if we mixed 95 ml distilled water, 5 ml Intralipid, 2 g Ager and 8.46 ul ink together, then we could obtain 100 ml solution which had an absorption coefficient of 0.021 mm−1 and a reduced scattering coefficient of 1.0 mm−1. This solution was further used to produce the absorber in this case. If we added 2.16 ul ink instead of 8.46 ul, the absorption coefficient of the solution was then 0.007 mm−1, which was used to produce the background medium. For cases 1–3, the single target had an absorption coefficient of 0.07 mm−1 and was located at a depth of 0.0, 4.8 and 7.6 mm below the surface, respectively. For case 4, the single target with an absorption coefficient of 0.035 mm−1 was embedded at a depth of 2.1 mm. For case 5, the single target having an absorption coefficient of 0.021 mm−1 was placed at a depth of 1.1 mm. For case 6, three targets with different absorption coefficients (0.07 mm−1, 0.035 mm−1 and 0.021 mm−1, respectively) were embedded at a depth of 1.9 mm. For all these cases, the absorption coefficient of the background was 0.007 mm−1 and the reduced scattering coefficient of the background and targets were 1.0 mm−1.

Animal experiments

Before the experiment of imaging the rat ear, one rat weighing 28 g was anesthetized using Urethane and the hairs of the ear were removed. The laser beam at 532 nm generated by a Nd:YAG laser was split into two sub-beams and coupled into two optical fiber bundles. A focused ultrasound transducer (50 MHz, 3 mm aperture and 6 mm focal length) was used to receive the induced photoacoustic waves. A 2D moving stage mounted with the optical fiber bundles and transducer carried out a 2D raster scanning. The raster scanning provided 200 A-lines along each direction with an interval of 60 μm over a distance of 12 mm. For the experiment of imaging the brain of a rat weighing 25–30 g, the brain area of interest was gently depilated and the scalp was removed before the imaging (Fig. 3(a)). Pulsed light at 1064 nm from the Nd:YAG laser and at 730 nm from the Ti:Sapphire laser were used for multispectral imaging. B-scan photoacoustic signals were recorded by a focused 50 MHz high-frequency transducer. During the imaging, the rat was anesthetized with Urethane (1 mg/g) and tightly positioned with a holder to avoid motion effect due to seizure activity. The body temperature of the animal was maintained at 37°C with a temperature controlling pad. At the end of study, all rats were sacrificed. All procedures have been approved by the University of Florida Institutional Animal Care and Use Committee (IACUC).

Image Reconstruction

Recovery of Absolute Optical Absorption Coefficient

Our PACM approach is based on a strategy that iteratively solves the radiative transfer equation (RTE) and the photoacoustic wave equation (PWE) using finite element method (FEM). In PACM, we first obtain the distribution of optical fluence, through the finite element (FE) solution to the RTE from an initial (guess) distribution of optical absorption coefficient, . For quantitative imaging of individual blood vessels, the use of RTE is necessary and most rigorous to model the light propagation in tissue since the absorption coefficient of blood vessels is high, making the commonly used photon diffusion equation inappropriate for quantitative PAM. The RTE used is described as follows:

where μs is the scattering coefficient; is the radiance; is the source term; denotes a unit vector in the direction of interest. The kernel, is the scattering phase function describing the probability density that a photon with an initial direction will have a direction after a scattering event. We assume that the scattering phase function depends only on the angle between the incoming and outgoing directions; thus the commonly used Henyey-Greenstein scattering function can be applied29: where γ is the angle between and and −1 < g < 1. The optical fluence is related to the radiance by .

Next, we computationally obtain the acoustic pressure, at each transducer location along the surface of the medium/tissue (rk(xk,yk), k = 1,2,…M transducer locations) using the following Helmholtz PWE30:

where p is the pressure wave; ν0 is the speed of acoustic wave in the medium; β is the thermal expansion coefficient; Cp is the specific heat; J(t) = δ(t−t0) is assumed in this study.

Finally, using the regularized Newton's method, the matrix equation for inversion of the absorption coefficient can be written as

where and are the observed and computed complex acoustic field data for k = 1,2…M transducer locations; Δχk is the update vector for the absorption coefficient; is the Jacobian matrix formed by ∂pk/∂χk at the boundary measurement sites; λ is the regularization parameter determined by combined Marquardt and Tikhonov regularization schemes31,32 (λ = 0.5 was used in this study–we have found that the quality of inversion was not sensitive to the choice of this parameter); and I is the identity matrix. Thus here an A-line image (χk(z) or μa,k(z)) is formed by updating absorption coefficient distribution via iterative solution of Eqs. (1)–(3) so that an object function composed of a weighted sum of the squared difference between computed and measured acoustic data can be minimized. A B-scan or 2D image is obtained by combining all the A-line images and a 3D image is provided by combining all the B-scan images. In these calculations, the incident laser source strength and the scattering coefficient μs are estimated in advance.

Recovery of Functional/Hemodynamic Parameters (HbR, HbO2, BF and MRO2)

In most cases for microvasculature imaging, HbO2 and HbR are the two major absorbers. Using multispectral measurements, the oxy- and deoxy-hemoglobin concentrations, [HbO2] and [HbR] can be obtained using the flowing well-known relationship33:

where εHbR(λ) and are the known molar extinction coefficients of HbR and HbO2 at wavelength λ. Oxygen saturation can be calculated as sO2 = [HbO2]/[HbT] where HbT is the total hemoglobin ([HbT] = [HbO2] + [HbR]).

We can further calculate the blood flow (BF) and rate of oxygen metabolism (MRO2) in blood vessels from the functional parameters obtained above. The method for such calculation is based on the principle of mass balance to the transport of oxygen in a blood vessel segment34. To model oxygen transport in a blood vessel by this principle, we consider a one-dimensional cylindrical vessel (blood vessel) with Ri and Ro as the inner and outer radii, respectively, surrounded by the biological tissues. In addition, we assume that all the oxygen (O2) diffusing out the segment is consumed in a tissue region35. The law of mass conservation stipulates that the amount of O2 lost from a vascular segment must be equal to the O2 flux diffused to the tissue, determined by the perivascular oxygen gradients. The oxygen consumed by the tissues (organs) is supplied from three blood vessels sources: capillaries, arterioles and venules. If the oxygen supply of tissues depends on the averaged oxygen saturation at the inlet and outlet of the tissues, tissue oxygen saturation should represent the weighted average of the arterial and venous saturation:

where sO2,ti and sO2,to are the averaged oxygen saturation at the inlet (artery) and outlet (vena) of the tissues, respectively. As such, mass balance for O2 in all tissues (organs) based on global analysis yields the following estimation of intravascular flux for a dynamic case, considering expressions of molar amount of oxy-hemoglobin concentration of tissue and tissue oxygen saturation:

where BF is the mean blood flow for all the blood vessels inside the tissues and is specified as the mean blood flow of tissues, OC = MRO2 is the mean oxygen consumption for the whole tissue, [HbT] is the mean total hemoglobin concentration in the tissues, [HbT]blood is the mean total hemoglobin concentration in the blood circulating through the tissues and V is the tissue volume and is assumed constant here. In our calculations, we assumed [HbT]blood = 0.72 mM, f = 0.2 and sO2,ti = 0.98. Further explanations on the determination of these parameters can be found elsewhere36.

Eq. (6) is the mathematical model we have developed for predicting BF and MRO2 from [HbT] and SO2. It is an ordinary partial differential equation that can be solved iteratively by Runge-Kutta 4th order method coupled with the FEM37. Thus, mean BF and MRO2 can be recovered by fitting Eq. (6) to time-resolved tissue oxygenation measurements. The fitting method is described as follows: with any given initial values for OC and BF within the specified range, this scheme is to optimize the OC and BF parameters based on the solution of Eq. (6) to reach the minimized objective function in Eq. (7):

in which is the measured oxygenation parameter from M discrete time points and is the oxygenation parameter calculated from Eq. (5) for the same M time points. Note that the BF and OC are assumed constant during the measurements for the specified time range, due to the need for a sufficient time interval to obtain stable fitting results.