Confirming the theoretical foundation of steady-state microbunching

Abstract

Steady-State Microbunching (SSMB) has been proposed as a concept to generate coherent synchrotron radiation at an electron storage ring. SSMB promises to supply kilowatt level average power radiation in the extreme ultraviolet regime, meeting the power level demands for lithography applications that presently cannot be fulfilled by established accelerator technologies. SSMB is under theoretical and experimental study, building on a proof-of-principle (PoP) experiment at the Metrology Light Source which previously showed the viability of the idea. Here we report experimental findings from systematic studies in the ongoing SSMB PoP experiment, where microbunching is generated from an energy modulation imposed by a laser of wavelength 1064 nm. The results confirm the expected dependence of the microbunching process on modulation amplitude and show that the influence of transverse-longitudinal coupling dynamics is as predicted. This confirmation of key parts of the SSMB theory establishes a solid footing for continuing the proof-of-principle efforts towards the goal of constructing a prototype SSMB light source facility.

Introduction

For applications in various fields of science and industry, there is rising demand for ultra-high brilliance X-ray radiation at high repetition rates^1,2,3. Additionally, computer chip manufacturers ask for high-power extreme-ultraviolet (EUV) radiation at ever shorter wavelengths to etch microscopic structures of ever smaller scale⁴. Over the last decades, such demands have pushed new ideas in accelerator technology for the generation of synchrotron radiation. To match this increasing demand, new ideas in accelerator technology for the generation of synchrotron radiation have emerged during the last decades. Major efforts have been directed towards improving Free Electron Lasers (FELs) for generating ultra-short, high peak power radiation pulses up to the hard X-ray regime^5,6,7,8. Recently, MHz-level pulse repetition rates have been realized on short timescales in FELs, a development promising for spectroscopy^9,10, but overall FELs cannot yet supply high average power radiation of kilowatt level at short wavelengths. Steady-State Microbunching (SSMB) has been proposed^11,12,13,14 to fill this gap. Starting from an electron storage ring with its inherently high repetition rate in the MHz range, SSMB invokes an optical laser modulator to replace the radio frequency cavity as the main longitudinal focusing element, creating persistent microbunches in the circular accelerator. In this way, high average power coherent radiation could be produced at significantly higher total efficiency and with less strict requirements to radiation safety than in a linear accelerator based FEL. With a suitable higher-harmonic generation scheme, the wavelengths of the generated radiation could reach the EUV regime^15,16, yielding an EUV radiation source with a power level suitable for lithography. SSMB could also serve as a source of high brightness, narrow bandwidth UV radiation for angle-resolved photoemission spectroscopy¹.

In this paper, we report on experimental findings in the SSMB Proof-of-Principle experiment that confirm key aspects of the current theoretical treatment of SSMB. We show that variations of the laser modulation strength yield the expected results, and that the influence of transverse-longitudinal coupling is as predicted. The latter is especially important towards a future realization of SSMB, since the most promising SSMB scheme currently proposed to realize high-power EUV radiation is based on a sophisticated application of transverse-longitudinal coupling dynamics for efficient microbunching generation¹⁷.

Results

SSMB proof-of-principle experiment

The fundamental concept behind SSMB is tested and evaluated in a proof-of-principle (PoP) experiment at the Metrology Light Source (MLS) that has shown very important positive results starting in 2019, proving the general viability of the concept^18,19.

The currently implemented setup at the MLS entails single turn modulation with a low repetition rate laser and generation of coherent radiation from unconfined microbunches, the electrons are not yet trapped within the individual microbunches. Conceptually this is similar to coherent harmonic generation schemes implemented at other accelerator labs^20,21, the main difference being that the whole circumference of the storage ring is used for the microbunching process. As such, the magnet settings of the whole storage ring that determine the overall beam parameters (such as emittance, lifetime) must also fulfill the requirements for microbunching generation. This is a necessary condition for achieving a steady state, as in this way the microbunches could be reinforced with further energy modulations on the following revolutions.

This will be attempted in a future phase of the SSMB PoP experiment, also to be installed at the MLS. Modulation on hundreds of consecutive turns using a high-repetition rate laser would lead to electrons performing synchrotron oscillations in individual microbunches, while not completely confined (no equilibrium, quasi-steady state). The new laser system required to provide turn-by-turn modulation is in preparation, to be installed at the MLS in the near future.

The final step would involve sustained modulation, over millions of revolutions, with electrons fully confined to microbunches (proper steady state reached). This is not possible with existing accelerator hardware, so this would be equivalent to the construction of a prototype SSMB accelerator facility that could already serve users. Such a prototype SSMB facility is in active design study at Tsinghua University, Beijing^{17,22,23,24,25,26,27}.

Setup at the Metrology Light Source

The MLS is an electron storage ring facility in Berlin, Germany (circumference 48 m, nominal beam energy 629 MeV). The accelerator has been optimized from design for short-bunch operation^28,29,30. Individually powered magnets and additional sextupole and octupole magnets provide unique operational flexibility essential for the implementation of electron beam optics necessary for SSMB PoP.

To enable the generation of microbunching in the experiment, the magnetic lattice of the electron storage ring (see Methods section) is adjusted to quasi-isochronous operation with very low phase slippage (∣η∣ < 2 ⋅ 10⁻⁵, see next section), such that the evolution of longitudinal structures is very slow. Making use of the unique flexibility of the MLS to control the higher orders of the momentum dependent phase slippage is crucial. The electron energy is reduced to 250 MeV to limit energy spread and the impact of longitudinal quantum excitation. Bunch charges are below 10 pC to minimize the impact of collective instabilities. For more details on the setup and theoretical background we would like to refer the reader to previous publications^18,31.

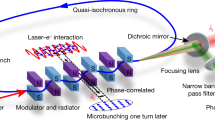
Figure 1 gives an overview of the currently implemented PoP experiment setup. Initial results were obtained by observing the second undulator harmonic (532 nm)¹⁸, as separating the modulation laser from the coherent undulator radiation on the first harmonic (1064 nm) is not trivial. A more sophisticated detection setup addressing this problem using electro-optical switches has been installed since and is available for systematic studies^19,32. The experiments reported here regard only the fundamental harmonic undulator radiation, detected by a fast photodiode (Femto HSPR-X-I-2G-IN, rise/fall time 180 ps) and oscilloscope (Tektronix MSO64, bandwidth 4 GHz, 25 billion samples per second).

Fig. 1: Schematic setup of the SSMB PoP experiment at the MLS.

A pulsed laser (wavelength 1064 nm, pulse width 5 ns FWHM, repetition rate 1.25 Hz) co-propagates with the electron beam through the MLS U125 undulator and imposes an energy modulation. The same undulator serves as a radiator on the following passes of the electron beam. The undulator radiation is detected by a fast photodiode, while the laser pulse is blocked from the detection path using an electro-optical switch. Figure adapted from previous publication¹⁸.

Theoretical considerations

Theoretical studies on the dynamics of SSMB have been extensive, as well as experimental investigations of several fundamental concepts relevant for SSMB^{31,33,34,35,36,37}. Some theoretical considerations are introduced in the following that provide the basis for the systematic investigations of microbunching dynamics as presented in this paper.

Bunching factor

Using single particle dynamics, the laser modulation and subsequent change of longitudinal position z (relative to the reference particle) can be described by the one-turn maps

$${\delta }_{m+1}={\delta }_{m}+{A}_{m}\sin \left({k}_{{{{{{{{\rm{L}}}}}}}}}{z}_{m}\right),$$

(1)

$${z}_{m+1}={z}_{m}-{C}_{0}\,\eta ({\delta }_{m+1})\,{\delta }_{m+1},$$

(2)

where δ = Δp/p₀ is the momentum deviation of the particle relative to a reference particle on the central orbit with momentum p₀, k_L = 2π/λ_L is the laser wave number, C₀ is the orbit circumference for the reference particle, and the index m refers to the revolution number. The phase slippage factor η = (ΔT/T₀)/δ represents the momentum-dependent change of the orbit revolution time relative to the reference particle traveling along the nominal circumference C₀ and with revolution time T₀. η is in general a non-linear function of the relative momentum deviation δ. A_m is the modulation amplitude on the m-th revolution, and in the current single-shot setup we have A₀ = A and A_m = 0 for m ≠ 0. The modulation is imposed by the electric field of the laser and is proportional to the square root of the instantaneous laser radiation power $A\propto \sqrt{{P}_{{{{{{{{\rm{L}}}}}}}}}}$.

We introduce the bunching factor b as a measure of the structuring of the longitudinal electron beam distribution at a wave number k. It is defined as the Fourier transform of the longitudinal particle distribution ρ(z):

$$b(k)=\int\nolimits_{-\infty }^{\infty }{{{{{{{\rm{d}}}}}}}}z\,{e}^{-ikz}\,\rho (z).$$

(3)

For an electron beam that has experienced a sinusoidal energy modulation as given by equations (1) and (2) the bunching factor b_n,m at the n-th harmonic of the laser wave number k_L and for the m-th revolution after modulation relates to the modulation amplitude A via a Bessel function of the first kind J_n³¹,

$${b}_{n,m}={J}_{n}(nm{k}_{{{{{{{{\rm{L}}}}}}}}}{\eta }_{0}{C}_{0}A)\exp \left[-\frac{{(nm{k}_{{{{{{{{\rm{L}}}}}}}}}{\eta }_{0}{C}_{0}{\sigma }_{\delta })}^{2}}{2}\right].$$

(4)

Note that here higher orders of the phase slippage have been neglected, η(δ) ≈ η₀, and a Gaussian momentum distribution ${\rho }_{0}(\delta )=\frac{1}{\sqrt{2\pi }{\sigma }_{\delta }}\exp \left(-\frac{{\delta }^{2}}{2{\sigma }_{\delta }}\right)$ is assumed with rms energy spread σ_δ.

Transverse-longitudinal coupling

Transverse particle oscillations may influence the longitudinal motion of particles and vice versa. This transverse-longitudinal coupling arises mainly because particles with different transverse displacements traverse different path lengths through the bending magnets. Due to this coupling, the transverse betatron oscillations can introduce an additional bunch lengthening³⁸. Considering only single-particle dynamics, the lengthening of a zero-length slice in the bunch resulting from transverse-longitudinal coupling after m revolutions around the ring can be quantified as³¹:

$$\Delta {z}_{m}=\sqrt{4{\epsilon }_{x}{{{{{{{{\mathcal{H}}}}}}}}}_{x}{\sin }^{2}(m\pi {\nu }_{x})+4{\epsilon }_{y}{{{{{{{{\mathcal{H}}}}}}}}}_{y}{\sin }^{2}(m\pi {\nu }_{y})}.$$

(5)

Here, ν_x,y are the horizontal and vertical betatron tunes (number of transverse oscillations per revolution), ϵ_x,y are the transverse beam emittances (see Methods section) and ${{{{{{{{\mathcal{H}}}}}}}}}_{x,y}$ are the horizontal and vertical chromatic functions at the modulator location defined as

$${{{{{{{{\mathcal{H}}}}}}}}}_{x,y}= {\gamma }_{x,y}{D}_{x,y}^{2}+2{\alpha }_{x,y}{D}_{x,y}{D}_{x,y}^{{\prime} }+{\beta }_{x,y}{D}_{x,y}^{{\prime} 2}\\ \approx \frac{1}{{\beta }_{x,y}}{D}_{x,y}^{2}+{\beta }_{x,y}{D}_{x,y}^{{\prime} 2},$$

(6)

and depending on the dispersion and dispersion angle ${D}_{x,y},{D}_{x,y}^{{\prime} }$. α_x,y, β_x,y and γ_x,y are the Courant-Snyder parameters³⁹ describing the transverse beam dynamics (see Methods section). The approximation can be made because α_x,y ≪ 1 at the modulator location.

This additional bunch lengthening can be incorporated into the exponential term of equation (4), yielding for the bunching factor at the m-th revolution and n-th laser harmonic³¹:

$${b}_{n,m}= {J}_{n}(nm{k}_{{{{{{{{\rm{L}}}}}}}}}{\eta }_{0}{C}_{0}A)\\ \cdot \exp \left[-\frac{{(n{k}_{{{{{{{{\rm{L}}}}}}}}})}^{2}}{2}\left\{{\left(m{\eta }_{0}{C}_{0}{\sigma }_{\delta }\right)}^{2}+4{\epsilon }_{x}{{{{{{{{\mathcal{H}}}}}}}}}_{x}{\sin }^{2}(m\pi {\nu }_{x})+4{\epsilon }_{y}{{{{{{{{\mathcal{H}}}}}}}}}_{y}{\sin }^{2}(m\pi {\nu }_{y})\right\}\right],$$

(7)

with

$${P}_{{{{{{{{\rm{coh}}}}}}}},n,m}\propto {\left\vert {b}_{n,m}\right\vert }^{2},\quad A\propto \sqrt{{P}_{{{{{{{{\rm{L}}}}}}}}}}\propto \sqrt{{E}_{{{{{{{{\rm{L}}}}}}}}}}$$

(8)

for the power of coherent synchrotron radiation P_coh and the instantaneous modulation laser power P_L that is proportional to the total laser pulse energy E_L, assuming that the pulse shape and timing is constant.

Equation (7) incorporates into one expression several conditions for the creation of microbunching and coherent radiation in the current SSMB PoP setup. In the following, we present the experimental investigation of four key components in relation (7), namely the dependence of the bunching factor b_n,m on A, ${{{{{{{{\mathcal{H}}}}}}}}}_{x}$, ϵ_y and ν_y.

Experimental results

All results presented here have been obtained using the first harmonic detection setup described in ref. ³² and employ a background subtraction scheme as detailed in the Methods section.

Influence of modulation amplitude

From the dependence of the bunching factor on the modulation amplitude via a Bessel function as shown in equation (7), we expect there to be an optimal modulation amplitude above which the coherent emission power will decrease again. Such a behavior was observed: Fig. 2a shows the coherent emission of a bunch train one turn after modulation with an approximate laser pulse as shown overlaid. As the modulation amplitude changes depending on the position of the electron bunch relative to the laser pulse, one can see a clear pattern of reduced emission for the central bunches experiencing maximum modulation amplitude. When the overall laser pulse energy is reduced, this pattern vanishes (as seen in Fig. 2b).

Fig. 2: Dependence of coherent emission power on laser modulation strength.

a, b coherent emission from individual bunches one turn after modulation (black, data averaged over 20 consecutive laser shots). Approximate laser pulse shape is overlaid as a guide (orange, shifted forward in time and scaled vertically to match coherent emission pulses). a maximum laser power, central bunches experience overbunching. b reduced laser power, no overbunching. c quantitative evaluation showing coherent emission from the central bunch marked CB, obtained for different overall laser pulse energies. Data points (black) show average over 50 consecutive laser shots. Error bars represent standard error of the mean. The blue curve is a fitted function of the type ${P}_{{{{{{{{\rm{coh}}}}}}}}}={a}_{1}{\left\vert {J}_{1}\left({a}_{2}\sqrt{{E}_{{{{{{{{\rm{L}}}}}}}}}}\right)\right\vert }^{2}$ with the Bessel function of the first kind J₁.

Figure 2c presents a quantitative analysis of this effect, showing the coherent undulator radiation emitted by one bunch (the central bunch denoted with CB in Fig. 2a, b) for different overall laser pulse energies. This is accomplished by rotating a half-wave plate between crossed polarizers, and the laser pulse energy is measured using a laser power meter in a diagnostic beam path in the detection area. Note that only a (constant) fraction of the laser pulse energy is incident there, so the actual power at the interaction point is higher than indicated, approximately by a factor of 2.

From equations (7) and (8) we expect for the relation between laser energy and emitted coherent radiation power

$${P}_{{{{{{{{\rm{coh}}}}}}}}}={a}_{1}{\left\vert {J}_{1}\left({a}_{2}\sqrt{{E}_{{{{{{{{\rm{L}}}}}}}}}}\right)\right\vert }^{2},$$

(9)

with parameters a₁ and a₂ that remain constant during the experiment. Fitting a function of this kind to the obtained experimental data yields good agreement.

Horizontal-longitudinal coupling

In order for the microbunching to not be destroyed from horizontal-longitudinal coupling it is crucial that the horizontal dispersion and dispersion angle are vanishing at the undulator. When varying the dispersion, from equations (6), (7), and (8) we can see that the coherent radiation power has a Gaussian dependence on D_x. Extracting only the horizontal-longitudinal coupling term we can write the following relation where we can identify the standard deviation ${\sigma }_{{D}_{x},m}$ of the coherent radiation power on the m-th revolution with respect to D_x:

$${P}_{{{{{{{{\rm{coh}}}}}}}},m}\propto \exp \left[-4{k}_{{{{{{{{\rm{L}}}}}}}}}^{2}\frac{{\epsilon }_{x}}{{\beta }_{x}}{\sin }^{2}(m\pi {\nu }_{x}){D}_{x}^{2}\right]=\exp \left[-\frac{{D}_{x}^{2}}{2{\sigma }_{{D}_{x},m}^{2}}\right].$$

(10)

A similar relation can be written for the dispersion angle ${D}_{x}^{{\prime} }$. Plugging in values for the storage ring conditions at the undulator location during the experiment β_x = 9.5 m, ϵ_x = 30 nm rad, ν_x = 3.18, we calculate theoretical values for these standard deviations of the coherent radiation power on D_x and ${D}_{x}^{{\prime} }$. We get for the first and second revolution after modulation:

$$\begin{array}{rcl}&&{\sigma }_{{D}_{x},1,{{{{{{{\rm{theo}}}}}}}}}=2.0\,{{{{{{{\rm{mm}}}}}}}},\,\,\quad {\sigma }_{{D}_{x}^{{\prime} },1,{{{{{{{\rm{theo}}}}}}}}}=0.21\,{{{{{{{\rm{mrad}}}}}}}},\\ &&{\sigma }_{{D}_{x},2,{{{{{{{\rm{theo}}}}}}}}}=1.2\,{{{{{{{\rm{mm}}}}}}}},\,\,\quad {\sigma }_{{D}_{x}^{{\prime} },2,{{{{{{{\rm{theo}}}}}}}}}=0.12\,{{{{{{{\rm{mrad}}}}}}}}.\end{array}$$

(11)

Figure 3 presents an experimental investigation on this dependence. Dispersion and dispersion angle are altered utilizing tuning knobs that transform a single input value to an array of differential current changes to be applied to the quadrupole magnets such that the dispersion or dispersion angle change independently in the undulator section. It should be noted that the horizontal axis scalings in Fig. 3 rely on calibration measurements of dispersion and dispersion angle (see Methods section) and thus carry statistical errors that are included in the calculation of the values below.

Fig. 3: Effect of longitudinal-horizontal coupling on coherent emission from microbunching.

Data points show coherent radiation power on the first (black crosses) and second (green circles) revolution after modulation. Data points are averaged over 20 consecutive laser shots, error bars represent standard error of the mean. a coherent emission vs. dispersion at the undulator. b coherent emission vs. dispersion angle at the undulator.

From fitted skew Gaussian curves we can calculate experimental values for the standard deviations on D_x and ${D}_{x}^{{\prime} }$:

$$\begin{array}{rcl}&&{\sigma }_{{D}_{x},1,\exp }=(4.12\pm 0.15)\,{{{{{{{\rm{mm}}}}}}}},\,\,\quad {\sigma }_{{D}_{x}^{{\prime} },1,\exp }=(0.49\pm 0.06)\,{{{{{{{\rm{mrad}}}}}}}},\\ &&{\sigma }_{{D}_{x},2,\exp }=(2.73\pm 0.09)\,{{{{{{{\rm{mm}}}}}}}},\,\,\quad {\sigma }_{{D}_{x}^{{\prime} },2,\exp }=(0.47\pm 0.05)\,{{{{{{{\rm{mrad}}}}}}}}.\end{array}$$

(12)

All experimental values are larger than the theoretical predictions. However, we do expect several effects to broaden the tolerances on D_x and ${D}_{x}^{{\prime} }$, such as transverse tilting of the microbunches when D_x or ${D}_{x}^{{\prime} }$ are non-zero, and the finite opening angle of the coherent radiation. Additionally, the theoretical values given in (11) could be inaccurate, as the values for β_x and ϵ_x are obtained from simulation only. With this in mind, we can state that there is good agreement with the theoretical expectation. The remaining discrepancy as well as the slight skew of the Gaussian curves and offset of the maxima between first and second revolution signals could also be attributed to small changes of the phase slippage function induced by the dispersion knobs, thereby additionally influencing the microbunching process.

Vertical-longitudinal coupling

Ideally, there should be no contribution from vertical-longitudinal coupling as the vertical dispersion D_y should be zero everywhere for a planar uncoupled ring like the MLS. However in reality we can get such a contribution because there is a small amount of coupling of horizontal motion to the vertical plane. Such coupling can arise from magnet alignment errors, such as tilted dipoles and offset sextupoles.

In experiment, we show the influence of vertical-longitudinal coupling on microbunching formation as described in equation (7) by regarding the impact of the vertical tune on the coherent emission after multiple revolutions. Figure 4 shows undulator radiation signatures over time for different settings of the vertical tune. For (a), it has been brought close to a fraction of five (ν_y ≈ 2.20), and as expected coherent emission is suppressed for all revolutions except for every fifth turn after modulation. Similarly for (b), close to a fraction of four (ν_y ≈ 2.25), revolution numbers at multiples of four are favored. At the standard vertical tune of the MLS (ν_y ≈ 2.23), we see an intermediary state favouring the fifth and fourth revolution (c). This pattern can be suppressed by carefully altering skew quadrupole currents to reduce the horizontal-vertical coupling, arriving in a state where the first revolution after modulation shows stronger coherent emission, with the signal decaying continuously on higher turns (d).

Fig. 4: Effect of longitudinal-vertical coupling on coherent emission from microbunching.

Datasets are averaged for 40 consecutive laser shots. a vertical tune ν_y ≈ 2.20. b ν_y ≈ 2.25. c ν_y ≈ 2.23 (standard MLS tune). d ν_y ≈ 2.23, horizontal-vertical coupling reduced by adjusting skew quadrupole magnets. The regular low power emission pattern on every turn, best visible in a and b, stems from the bunch train filling pattern with 20 out of 80 bunches populated and is the incoherent undulator radiation emanating from unmodulated bunches. Note the different vertical axis scales that use arbitrary but comparable units.

Similar findings have been made in laser bunch slicing experiments at the electron storage ring UVSOR⁴⁰, and the underlying mechanism of transverse-longitudinal coupling is similar. However, we point out that due to the shorter wavelength of the radiation (micrometer level), the manipulation of transverse-longitudinal coupling dynamics as presented here is three orders of magnitude more precise than for bunch slicing experiments that observe Terahertz radiation, as the one at UVSOR⁴⁰.

We can also regard the impact of the beam emittance as present in equation (7). The vertical emittance is increased by applying a vertical white noise excitation to the beam via a stripline, thereby exciting uncorrelated vertical oscillations. Figure 5 shows the impact of such an excitation on the coherent undulator radiation from the first six revolutions after modulation, starting from a coupling-corrected state as in Fig. 4d with ν_y ≈ 2.23. As the emittance increases, the impact of vertical-longitudinal coupling becomes more significant and suppresses microbunching formation for all revolutions, except for the fourth and fifth revolution. Here, the sinusoidal term in equation (7) is small, because the vertical tune is close to fractions of four and five. Thus the emittance would have to be increased further to see the same level of reduction of coherent radiation power. This is illustrating the same effect as explained above and shown in Fig. 4.

Fig. 5: Influence of vertical emittance on multi-turn coherent emission.

Horizontal axis is vertical beam size measured at a source point imaging system, proportional to the square root of vertical emittance. Data points show average over 40 consecutive laser shots. Error bars represent standard error of the mean. Solid lines are fitted theoretical curves (see text). The storage ring setup corresponds to the case shown in Fig. 4d.

Applying equation (7), we can make a quantitative comparison with theory. Combining all terms other than the vertical-longitudinal coupling term into one multiplicative constant, we can write for the expected coherent radiation power on the first harmonic for the m-th revolution after modulation:

$${P}_{{{{{{{{\rm{coh}}}}}}}},m}={c}_{m}\cdot \exp \left[-4{k}_{{{{{{{{\rm{L}}}}}}}}}^{2}{\epsilon }_{y}{{{{{{{{\mathcal{H}}}}}}}}}_{y}{\sin }^{2}(m\pi {\nu }_{y})\right].$$

(13)

We can calculate the emittances from the measured vertical rms beam sizes σ_y via the beta function at the position of the source point imaging system as ${\epsilon }_{y}={\sigma }_{y}^{2}/{\beta }_{y}$ (see Methods section). The only unknowns in equation (13) are ${{{{{{{{\mathcal{H}}}}}}}}}_{y}$ and c_m, which we can attempt to fit to the experimental data. For the first revolution data (blue curve in Fig. 5), ${{{{{{{{\mathcal{H}}}}}}}}}_{y}$ and c₁ are fitted, yielding ${{{{{{{{\mathcal{H}}}}}}}}}_{y}=(8.1\pm 0.4)\,\mu {{{{{{{\rm{m}}}}}}}}$. This value is on the expected order of magnitude when comparing to the horizontal-longitudinal coupling results. For the higher revolutions, we use the same value of ${{{{{{{{\mathcal{H}}}}}}}}}_{y}$ and only fit c_m. The gradients of the fitted curves (solid lines in Fig. 5), given by ${{{{{{{{\mathcal{H}}}}}}}}}_{y}$ via equation (13), fit well with the experimental data for all revolutions. This again confirms the prediction given by equation (7).

For the smallest beam sizes in Fig. 5, there is some discrepancy with the theoretical curves, with a reduction of measured coherent radiation power. This is most likely due to intra-beam scattering or other collective effects: Increasing vertical emittance by applying white noise excitation may reduce the bunch length or energy spread, both leading to enhanced microbunching. This hypothesis is supported by the observation that horizontal beam size decreases slightly when the white noise excitation is applied.

We point out that transverse-longitudinal coupling (TLC) does not necessarily need to be suppressed to enable the microbunching formation. In fact, the coupling dynamics could be exploited in a subtle way to enhance microbunching, such as by partially exchanging emittance between the longitudinal and transverse planes. In the generalized longitudinal strong focusing scheme for SSMB¹⁷, TLC is proposed to be applied for efficient high harmonic generation with a relaxed requirement on modulation laser power compared to other schemes, by taking advantage of the ultra-small vertical emittance in a planar electron storage ring. A lower requirement on laser power allows the laser modulator of SSMB to work with a high duty cycle or in continuous wave mode, thus allowing a higher filling fraction of microbunched electrons in the ring, increasing the output average radiation power. At the moment, this is the most promising SSMB scenario to obtain high-power EUV radiation, and TLC is its backbone.

Conclusions

We have shown that the influence of transverse-longitudinal coupling in the SSMB PoP setup corresponds to the theoretical expectation in multiple aspects, and can be manipulated with high accuracy. This is crucial for generalized longitudinal strong focusing¹⁷, the most promising SSMB scheme currently proposed, but can also be of interest in the wider field of accelerator physics. Additionally, the dependence on laser modulation strength is as expected, thus confirming the theoretical description of the microbunching mechanism to be accurate.

These results bring the first phase of the SSMB PoP experiment using single shot modulation close to a conclusion. The last open question remaining before moving on to exploring turn-by-turn modulation is the issue of shot-by-shot signal stability. Presently, under constant experiment conditions, the observed coherent radiation intensity fluctuates significantly between modulation events, with rms fluctuations of 10% up to 100% not uncommon. This is a key issue for the future applicability of SSMB, as users will demand stable radiation conditions. Efforts to understand and improve stable conditions for microbunching will be intensified. Currently, the most probable candidate explanation are fluctuations of the phase slippage originating from output ripple in the magnet power supplies.

Meanwhile, preparations for the next phase of the SSMB PoP experiment are ongoing. The laser system that will provide turn-by-turn modulation is completed and is undergoing final commissioning and tests before installation at the MLS will proceed. Integration of the new laser is planned in parallel to the existing laser system, also allowing single shot modulation experiments to continue.

Overall, the presented findings are supportive of the established theory for SSMB and constitute step forward in the ongoing efforts to realize an SSMB coherent synchrotron radiation light source.

Methods

Courant-Snyder parameters and emittance

The transverse beam dynamics in a circular accelerator are described in horizontal or vertical phase space, spanned by transverse position x(s) and angular divergence ${x}^{{\prime} }(s)={{{{{{{\rm{d}}}}}}}}x/{{{{{{{\rm{d}}}}}}}}s$. Here, we regard the horizontal plane, but all relations also hold in the vertical plane (x → y). The equations of motion for the transverse beam dynamics restrain particles to move on an ellipse in phase space for any given position along the storage ring s. An example for such an ellipse is shown in Fig. 6. A convenient choice to express the periodic solutions for the equations of motion are the Courant-Snyder parameters α_x(s), β_x(s), and γ_x(s), as these directly parametrize the phase space ellipse³⁹:

$${\gamma }_{x}{x}^{2}+2{\alpha }_{x}x{x}^{{\prime} }+{\beta }_{x}{x}^{{\prime} 2}={\epsilon }_{x}^{(i)}.$$

(14)

Here, i is a particle index and ${\epsilon }_{x}^{(i)}={{{{{{{\rm{const.}}}}}}}}$ is the single particle emittance, or Courant-Snyder invariant of this particular particle. The area of the ellipse is given by the emittance as $\pi {\epsilon }_{x}^{(i)}$. From equation (14) one can find expressions for the maximum displacement ${x}_{\max }$ and the maximum angular divergence ${x}_{\max }^{{\prime} }$:

$${x}_{\max }(s)=\sqrt{{\epsilon }_{x}^{(i)}\beta (s)},$$

(15)

$${x}_{\max }^{{\prime} }(s)=\sqrt{{\epsilon }_{x}^{(i)}\gamma (s)}.$$

(16)

When regarding a distribution of many particles, one can choose a beam emittance ϵ_x that represents the distribution of all single particle emittances ${\epsilon }_{x}^{(i)}$. Keeping consistency with other sources^31,38 and major simulation codes we define the beam emittance as

$${\epsilon }_{x}=\left\langle \frac{{\epsilon }_{x}^{(i)}}{2}\right\rangle ,$$

(17)

such that we can write for the rms beam width σ_x:

$${\sigma }_{x}(s)=\sqrt{{\epsilon }_{x}{\beta }_{x}(s)}.$$

(18)

Fig. 6: Transverse phase space ellipse with Courant-Snyder parameters.

Example for the horizontal plane at one location in the storage ring. The emittance ϵ_x gives the area of the ellipse, while the Courant-Snyder parameters β_x and γ_x are connected with the beam envelope and angular spread of the beam.

Storage ring setup

The magnetic lattice of the MLS storage ring as well as the optical functions employed in the SSMB PoP experiment are shown in Fig. 7. The MLS is composed of four double-bend achromat (DBA) cells, with two bending dipole magnets each. The quadrupole magnets at the center of the DBA structure (Q1 quadrupoles) are primarily used to adjust the phase slippage. The horizontal and vertical beta functions at the locations of the Q1 quadrupoles are low, thus their impact on transverse dynamics is minimal, while the horizontal dispersion is large, maximizing the impact on longitudinal dynamics. Selective adjustments of adjacent Q1 quadrupoles allow to change the dispersion and dispersion angle in the undulator section. Skew quadrupole coils employed to influence horizontal-vertical coupling are integrated into select sextupoles (see Fig. 7).

Fig. 7: Magnetic lattice of the Metrology Light Source and optical functions in the steady-state microbunching proof-of-principle experiment.

Curves for horizontal and vertical beta functions β_x (red), β_y (blue) and horizontal dispersion D_x (green) are obtained from a simulation model. In the experiment, laser modulation and generation of coherent radiation occur at the undulator (s = 12 m), where D_x ≈ 0.

Evaluation of coherent undulator radiation signals

The (coherent) undulator radiation is detected using a fast photodiode and recorded with a sampling oscilloscope. To extract singular values for the detected radiation power, multi step data processing is employed.

First, background signals are removed for each individual oscilloscope trace in regions of interest around multiples of the MLS revolution time (160 ns) after the laser pulse. A median filter of 2 ns width, corresponding to the electron bunch spacing, is applied to obtain the slowly changing background signal. The filtered data is subtracted from the raw data, leaving only structures changing faster than the bunch spacing (see Fig. 8a for an example).

Fig. 8: Background correction applied to the undulator radiation data.

a exemplary raw photodiode data trace (black) and data with background removed, employing a median filter (light blue). Overview of data in a region of interest one revolution time (160 ns) after the laser pulse. The broad, double peak structure is caused by a weak laser reflection. b detail around one light pulse from a single electron bunch, showing the individual oscilloscope sampling points. c Background corrected data obtained for 10 consecutive laser shots showing shot-by-shot signal fluctuation. Individual data sets are shown with different colors.

Averaging is performed for consecutive full data traces in the regions of interest to allow weak signals below the noise floor to be detected. For both averaged and individual background corrected traces, the signal heights of each radiation pulse is extracted as the maximum sampling point in a predefined 2 ns range. This is possible because the sampling point density is high enough relative to the pulse duration (see Fig. 8b). The additional error made by taking the maximum sample as opposed to employing Gaussian fits is negligible against the shot-by-shot fluctuation of the coherent emission power (see Fig. 8c).

We give the standard error of the mean as error bars for the pulse heights averaged over a specified number of events. The rms fluctuation of pulse heights from individual measurements over the same period is used to estimate the uncertainty of a single sample.

Calibration of dispersion knobs

To alter dispersion and dispersion angle at the undulator for the horizontal-longitudinal coupling studies, tuning knobs are employed that transform a single input value to an array of differential current changes to be applied to the quadrupole magnets. To know the actual change of dispersion and dispersion angle when using the knobs, we perform a calibration. Dispersion and dispersion angle are measured by slightly altering the rf frequency, thereby inducing a change of beam momentum, and observing the difference in orbit position at beam position monitors (BPMs). The values at the undulator center can be interpolated from nearby BPMs. Figure 9 shows the resulting calibration curves with linear fits applied to obtain the calibration factors.

Fig. 9: Calibration of dispersion and dispersion angle knobs.

Data points (black) show dispersion or dispersion angle measured for different settings of the knobs. Error bars are obtained via error propagation from the statistical uncertainties of the beam position monitors. Red lines are linear fits. a calibration of the dispersion knob, b calibration of the dispersion angle knob.