Introduction

Major engineering construction projects (hereinafter referred to as mega projects) are projects with large investment scales, long implementation periods, high technical complexity, and far-reaching impact on the social economy and ecological environment (Flyvbjerg, 2014; Sheng, 2018). Compared with general engineering projects, mega projects have multi-dimensional, multi-level, and multi-stage complexity (Van Marrewijk et al., 2008; Sheng et al., 2019). There are many problems in the governance of mega projects, among which the collusion of the participants to obtain additional benefits is one of the most popular problems (Sheng et al., 2019; Yang and Wang, 2006).

In China, the construction of mega projects is mainly a commissioned-agent construction system. The government implements the management function of the project through the formation of owners to represent the government. In this way, the government and the owner form a principal–agent relationship. The owner entrusts the construction unit to carry out the project construction and the supervisor to carry out the monitoring work. When the owner and the construction party form a collusion, the supervision unit may be dismissed by the owner. Because the owner has the information advantage, and based on the consideration that the possibility of collusion exposure is small and the benefit of collusion is far greater than the opportunity cost and so on, the supervisor often chooses to join the collusion (Cao et al., 2014). At this time, the owner, the construction party, and the supervisor may form a collusion-body. Obviously, such collusive action poses a great risk to major engineering projects and has buried huge security risks (Yang and Wang, 2006).

From a larger perspective, the collusive behavior in the construction of mega projects is a problem of engineering governance. In the time dimension of engineering governance, some scholars believe that the governance should be carried out from the whole life cycle of mega projects to solve the collusion problem (Zhao et al., 2022; Gao et al., 2022; Chen et al., 2020), among them, we can learn from the artificial intelligence method based on digital technology (Wang et al., 2022), fuzzy cognitive mapping technology (Kordestani Ghaleenoei et al., 2022) and so on. In terms of governance mechanisms, it is necessary to build action criteria, organizational procedures, and joint action mechanisms for major project decision-making (Li et al., 2019) and discuss the core connotation and derivative issues of the integration and unification of governance modernization and Sinicization (Sheng et al., 2020). In the theoretical system of major project management, the organizational model should be innovated under the Chinese background (Le et al., 2019). For example, the social governance framework of mega projects based on “enterprise–government–society” should be constructed for the social responsibility of mega projects (Ma et al., 2017); the governance mechanism and evolution process under the dual role of “government-market” are studied for the major engineering organization model (Le et al., 2019). Against the background of institutional complexity, some scholars put forward a variety of governance mechanisms to alleviate the conflicts caused by the complexity of mega projects (Qiu et al., 2019; Ahola et al., 2014). These studies focus on the theoretical logic or practical problems in specific aspects of mega projects and lay a foundation for the study of collusion in mega project governance.

The main participants of mega projects include not only the owners, construction party, and the supervisor, but also the government and the public. The government should play an active role in the construction of mega projects. One is to strengthen supervision, for example, strict management of project costs and construction funds, giving full play to the supervisory role of auditing and supervision and strengthening the disciplinary accountability of safety and quality accidents (Luo et al., 2021). The other is to make information public. Governments at all levels can timely disclose construction, quality and safety supervision, and other information through government bulletins, government websites, press conferences, etc. (He et al., 2020). Xiao and Hao (2022) believe that the construction of mega projects constitutes an engineering community, and the government, as the core actor, must actively intervene and adopt strategies such as open cooperation, value recognition, and strict supervision to better maintain the operation and stability of the community. The public, as the direct beneficiary of major engineering projects, should also play its due supervisory role. When the public participates in the supervision of major projects, the public will naturally become the main participant of major projects. With the development of social media, there are more channels for the public to participate in the construction of major engineering projects. The public can also participate in the supervision of major engineering projects by attending hearings, conducting field visits, and filing complaints with regulatory authorities.

Due to the large number of participants in major construction projects, the diversity of stakeholders leads to the complexity of the decision-making behavior of the participants (Shen and Xue, 2021). The owner, the construction party, and the supervisor may obtain greater benefits through collusion (Yang et al., 2006). Based on the balance of costs and benefits, the government may take active intervention actions, such as strict supervision and timely release of relevant information. But it may also take the form of formal intervention, for example, a mere formality of regulation and a failure to release relevant information in a timely manner (Jiang et al., 2017). The public may also adopt supervision or non-supervision behavior due to considerations of the costs and benefits (Shen and Zhou, 2022). Whether the public participates in supervision or not is an act of decision-making alone, which does not represent the behavior of the government. The public involved in mega projects is usually divided into four types: people affected by the project or suspected of being affected by the project, experts and scholars, social organizations, and news media (Zhang et al., 2018). Obviously, the active involvement of the government and public supervision can help reduce the possibility of collusion.

Evolutionary game theory is a powerful tool to study the behavior of participants in mega projects. Evolutionary game requires the game subject to have limited rationality, and the game equilibrium is realized through the imitation and mutation of the subject. Sun and Sun (2021) studied the game model of strategic interaction between local governments and the public in mega projects and thought that the improvement of the convergence speed of the game could reduce the cost of both sides, thus improving supervision efficiency and reducing the occurrence of collusion. Li and Zhang (2021) incorporated the public supervision subsidy into the model, built a tripartite evolution game model of mega projects among the government, the contractor, and the public, and analyzed the gradual stability conditions of all parties involved in the project construction stage. Based on the digital construction situation, Lv and Wang (2022) built a game model of the contraction party, the supervisor, and the contractor from the perspective of major project supervision, and discussed the influence of different external variables on the three parties involved. Cheng et al. (2017) constructed an evolutionary game model of the government, the owner, the contractor, and the supervisor in the case of collusion in view of the two types of supervision models, and discussed the optimal probability of collusion and the optimal probability of government supervision. However, these papers do not include the owner, the construction party and the supervisor, the government, and the public into a framework, and then study the evolutionary game behavior of these participants.

Different from other papers, this paper takes the owner, the construction party, and the supervisor in a major project as possible collusion whole (hereinafter referred to as “collusion-body”), assigns the probability of the collusion possibility to the collusion-body, and then builds a tripartite evolutionary game model of “collusion-body”–government–public, studies the strategic stability of the parties involved, and simulates the influence of decision variables on the game. The study on the evolution of the game behavior of the collusion-body, the government and the public are helpful to prevent collusive behavior in the governance of major engineering projects.

Model building

Problem description

In the construction of mega projects, the owner, the construction party, and the supervisor form a collusion-body with a certain probability. When making strategy selection, the collusion-body, the government, and the public will choose the game strategy according to their own cost and benefit situation and the possible behavior of other participants, and the goal is to maximize the benefits. The purpose of this paper is to explore the stability strategy of the game system composed of the collusion-body, the government, and the public and what variables affect the stability of the game, and providing management enlightenment for the governance of collusive behavior of mega projects.

In the case of collusion-body, non-colluding behavior also generates normal costs (C12) and normal rewards (R11). If the collusion-body colludes, there will also be costs (C11) and additional income (R12), but there will be a reduction in costs (C12 > C11). In addition, if the collusive behavior is exposed by the government or the public, it will bring its own losses (L1), such as the decline of credit rating and social influence; The collusion-body will also face fines (P1) and compensation to the public (R31) after their collusion is exposed. After weighing the cost and benefit, the collusion-body chooses the game strategy according to the maximization of their own interests.

The government also chooses the game strategy according to the maximization of its own interests. Active government intervention generates costs (C21), but also additional benefits (R2), including reputation benefits and superior rewards. Formal government intervention also has costs (C22), but no benefits. Generally, the cost of active government intervention is greater than the cost of formal government intervention (C21 > C22). There will also be other costs for the government. The government sets up owners to implement major engineering projects, but the owner conspires with the construction party and supervisor to obtain improper benefits, and the government faces direct losses (L22). Because the government takes an inactive general intervention strategy to allow the collusive behavior to occur, it will also lead to the loss of the government’s reputation and public trust (L21), the punishment from the superior (P2), and the government’s compensation for the loss to the public (R33). In view of the great harm of the collusive acts, the fine of the collusive parties is generally greater than the compensation of the government for the public losses (P1 > R33).

The public’s choice of game strategy will also face the trade-off of cost and benefit, but it is relatively simple. Public participation in supervision will incur costs (C3), but it will also receive incentives from the government (R32). Major engineering projects are in the public interest and when collusion occurs, the public interest will suffer (L3). Meanwhile, the compensation of the collusion-body to the public (R31) and the compensation of the government to the public loss (R33) form the public benefit. Generally, the public benefit from compensation is greater than the public supervision cost (R31 + R33 > C3). Table 1 shows the relevant symbols and meanings.

Table 1 Parameters description of model.
Full size table

Model assumptions

To describe the decision-making behavior of each participant, the following assumptions are proposed:

(1) The main participants of major engineering construction projects include the collusion-body composed of the owner, the construction party and the supervisor, the government, and the public. There is a game relationship among the collusion-body, the government, and the public, and the three parties have limited rationality in the game. Game is dynamic, participants dynamic constantly adjust their strategies until reach the evolutionary stable strategy (ESS).

(2) In the game, the collusion-body, the government, and the public can choose two strategies. The collusion-body chooses strategies according to the goal of maximizing benefits. If they think the benefits can be maximized, they will choose the “collude” strategy. If it is believed that the collusive behavior cannot achieve the maximum benefit, the “not to collude” strategy will be chosen, and the strategy set is {collude, not to collude}. Similarly, the government will choose “active intervention” or “formal intervention” based on the cost-benefit situation, and its strategy set is {active intervention, formal intervention}. By weighing the cost and benefit, the public chooses to participate in supervision or not participate in supervision, and its strategy set is {participate, not to participate}.

(3) In the game, the probability of the collusion-body, the government, and the public to choose a certain strategy is measured by probability. The probability of the set of collusion-body strategies {collude, no to collude} is {x, 1−x}. The probability of the government policy set {active intervention, formal intervention} is {y, 1−y}. The public policy set {participate, not to participate} corresponds to the probability {z, 1−z}, where 0 ≤ x, y, z ≤ 1.

(4) In the game, the costs, benefits, fines, losses, compensation, and other costs involved by the collusion-body, the government, and the public can be quantified and are all positive.

Evolutionary game payment matrix

According to the above assumptions, the eight strategy combinations of the tripartite game between the collusion-body, the government, and the public in mega projects can be obtained. The payment matrix is shown in Table 2.

Table 2 Payoff matrix among the collusion-body, the government, and the public.
Full size table

Replicated dynamic equation

Suppose that the expected payoffs of the collusion-body selecting “collude” and “not to collude” strategies, are represented by U11, U12, respectively. Then U11 and U12 can be obtained from the payoff matrix as follows:

$$\begin{array}{l}U_{11} = yz\left( { - C_{11} + R_{11} + R_{12} - L_1 - P_1 - R_{31}} \right)\\ \qquad\quad+ \,y\left( {1 - z} \right)\left( { - C_{11} + R_{11} + R_{12} - L_1 - P_1 - R_{31}} \right)\\ \qquad\quad+ \,\left( {1 - y} \right)z\left( { - C_{11} + R_{11} + R_{12} - L_1 - P_1 - R_{31}} \right)\\ \qquad\quad+\, \left( {1 - y} \right)\left( {1 - z} \right)\left( { - C_{11} + R_{11} + R_{12}} \right)\end{array}$$
(1)
$$\begin{array}{ll}U_{12} = yz\left( { - C_{12} + R_{11}} \right) + y\left( {1 - z} \right)\left( { - C_{12} + R_{11}} \right)\\ \qquad\quad+ \,\left( {1 - y} \right)z\left( { - C_{12} + R_{11}} \right) + \left( {1 - y} \right)\left( {1 - z} \right)\left( { - C_{12} + R_{11}} \right)\end{array}$$
(2)

The average expected payoffs are denoted by \(\overline {U_1}\):

$$\overline U _1 = xU_{11} + \left( {1 - x} \right)U_{12}$$
(3)

Based on Eqs. (1)–(3), the replicator dynamic equation of the collusion-body can be denoted as follows:

$$\begin{array}{l}F\left( x \right) = \frac{{{\rm {d}}x}}{{{\rm {d}}t}} = x\left( {U_{11} - \overline U _1} \right) = x\left( {1 - x} \right)\left[ z\left( {y - 1} \right)\left( {L_1 + P_1 + R_{31}} \right)\right.\\\left. \qquad\qquad- \,y\left( {L_1 + P_1 + R_{31}} \right) - C_{11} + C_{12} + R_{12} \right]\end{array}$$
(4)

Suppose that the expected payoffs of the government selecting “active intervention” and “ formal intervention” strategies, are represented by U21, U22, respectively. Then U21 and U22 can be obtained from the payoff matrix as follows:

$$\begin{array}{l}U_{21} = xz\left( {C_{21} + R_2 + P_1 - L_{22} - R_{32} - R_{33}} \right) + \left( {1 - x} \right)z\left( { - C_{21} + R_2 - R_{32}} \right)\\ \qquad\quad+ \,x\left( {1 - z} \right)\left( { - C_{21} + R_2 + P_1 - L_{22} - R_{33}} \right) + \left( {1 - x} \right)\left( {1 - z} \right)\left( { - C_{21} + R_2} \right)\end{array}$$
(5)
$$\begin{array}{l}U_{22} = xz\left( { - C_{22} + P_1 - L_{21} - L_{22} - P_2 - R_{33}} \right) + \left( {1 - x} \right)z\left( { - C_{22}} \right)\\ \qquad\quad+\, x\left( {1 - z} \right)\left( { - C_{22} - L_{22}} \right) + \left( {1 - x} \right)\left( {1 - z} \right)\left( { - C_{22}} \right)\end{array}$$
(6)

The average expected payoffs are denoted by \(\overline {U_2}\):

$$\overline U _2 = yU_{21} + \left( {1 - y} \right)U_{22}$$
(7)

Based on Eqs. (5)–(7), the replicator dynamic equation of the government can be denoted as follows:

$$\begin{array}{ll}F\left( y \right) = \frac{{{\rm {d}}y}}{{{\rm {d}}t}} = y\left( {U_{21} - \overline U _2} \right) = y\left( {1 - y} \right)\left[ xz\left( {L_{21} - P_1 + P_2 + R_{33}} \right)\right.\\ \left.\qquad\qquad+ \,x\left( {P_1 - R_{33}} \right) - zR_{32} + C_{22} - C_{21} + R_2 \right]\end{array}$$
(8)

Suppose that the expected payoffs of the public selecting “participate” and “not to participate” strategies, are represented by U31, U32, respectively. Then U31 and U32 can be obtained from the payoff matrix as follows:

$$\begin{array}{l}U_{31} = xy\left( { - C_3 + R_{31} + R_{32} - L_3 + R_{33}} \right)\\ \qquad\quad+ \,x\left( {1 - y} \right)\left( { - C_3 + R_{31} - L_3 + R_{33}} \right) + \left( {1 - x} \right)\,y\left( { - C_3 + R{}_{32}} \right)\\ \qquad\quad+ \,\left( {1 - x} \right)\left( {1 - y} \right)\left( { - C_3} \right)\end{array}$$
(9)
$$U_{32} = xy\left( {R_{31} - L_3 + R_{33}} \right) + x\left( {1 - y} \right)\left( { - L_3} \right)$$
(10)

The average expected payoffs are denoted by \(\overline {U_3}\):

$$\overline U _3 = zU_{31} + \left( {1 - z} \right)U_{32}$$
(11)

Based on Eqs. (9)–(11), the replicator dynamic equation of the public can be denoted as follows:

$$F\left( z \right) = \frac{{{\rm {d}}z}}{{{\rm {d}}t}} = z\left( {U_{31} - \overline U _3} \right) = z\left( {1 - z} \right)\left[ { - xy\left( {R_{31} + R_{33}} \right) + yR_{32} + x\left( {R_{31} + R_{33}} \right) - C_3} \right]$$
(12)

Consequently, according to Eqs. (4), (8) and (12), a three-dimensional dynamic system of the collusion-body, the government, and the public can be constructed as follows:

$$\left\{ \begin{array}{l}F\left( x \right) = \frac{{{\rm {d}}x}}{{{\rm {d}}t}} = x\left( {1 - x} \right)\left[ {z\left( {y - 1} \right)\left( {L_1 + P_1 + R_{31}} \right) - y\left( {L_1 + P_1 + R_{31}} \right) - C_{11} + C_{12} + R_{12}} \right]\\ F\left( y \right) = \frac{{{\rm {d}}y}}{{{\rm {d}}t}} = y\left( {1 - y} \right)\left[ {xz\left( {L_{21} - P_1 + P_2 + R_{33}} \right) + x\left( {P_1 - R_{33}} \right) - zR_{32} + C_{22} - C_{21} + R_2} \right]\\ F\left( z \right) = \frac{{{\rm {d}}z}}{{{\rm {d}}t}} = z\left( {1 - z} \right)\left[ { - xy\left( {R_{31} + R_{33}} \right) + yR_{32} + x\left( {R_{31} + R_{33}} \right) - C_3} \right]\end{array} \right.$$
(13)

Model analysis

Strategic stability analysis of the collusion-body

In Eq. (4), let F(x) = 0, then we can obtain x* = 0, x* = 1 and

$$z \ast = \frac{{y\left( {L_1 + P_1 + R_{31}} \right) + C_{11} - C_{12} - R_{12}}}{{\left( {y - 1} \right)\left( {L_1 + P_1 + R_{31}} \right)}}$$
(14)

It can be obtained from formula (14):

Proposition 1 There is a relationship between the costs difference of collusion (C12−C11) and the additional benefits R12 brought by collusion and the probability of public participation in supervision: (i) \(\frac{{\partial z^ \ast }}{{\partial \left( {C_{12} - C_{11}} \right)}} > 0\), which indicates that when the difference between the costs of non-collusion and the costs of collusion increase, the probability of public participation in supervision will increase; (ii) \(\frac{{\partial z^ \ast }}{{\partial R_{12}}} > 0\), which indicates that the probability of public participation in supervision will increase when the additional benefits of collusion increase under other conditions unchanged.

Further, derive for F(x), then we can obtain as follows:

$$\begin{array}{ll}F{\prime}\left( x \right) = \frac{{{\rm {d}}F\left( x \right)}}{{{\rm {d}}x}} = \left( {1 - 2x} \right)\left[ z\left( {y - 1} \right)\left( {L_1 + P_1 + R_{31}} \right)\right. \\ \left.\qquad\qquad-\, y\left( {L_1 + P_1 + R_{31}} \right) - C_{11} + C_{12} + R_{12} \right]\end{array}$$
(15)

Therefore, the evolutionary stability strategy of the collusion-body can be discussed, which is analyzed in the following three cases.

  1. (1)

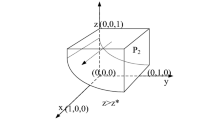
    When 0 < z = z* < 1, F(x) ≡ 0, at this time, any value of x(0 ≤ x ≤ 1) is ESS. The replicated dynamic phase diagram of the collusion-body is shown in Fig. 1a. The shaded surface in the diagram divides the strategy space into two regions, I and II, and the ESS of the collusion-body is located on the shaded surface, which indicates that when the probability of public participation in supervision is a fixed value z*, although the probability of collusion is not certain, it is in a stable state.

    Fig. 1: Evolution phase diagram of collusion-body strategy behavior.
    figure 1

    Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures reflect the change of the collusion-body’s strategy choice with the change of the public’s strategy choice, where the arrow indicates the direction of the collusion-body’s strategy change.

    Full size image
  2. (2)

    When 0 < z < z* < 1, F′(0) > 0, F′(1) < 0, at this point, x* = 1 is ESS. The corresponding replication dynamic phase diagram is shown in Fig. 1b. At this time the initial state of the collusion-body is in the strategy space I region, but it will eventually choose to collude.

  3. (3)

    When 0 < z* < z < 1, F′(0) < 0, F′(1) > 0, at this point, x* = 0 is ESS. The corresponding replication dynamic phase diagram is shown in Fig. 1(c). At this time, the initial state of the collusion-body is in the strategy space II region, but it will eventually choose not to collude.

Strategic stability analysis of government

In Eq. (8), let F(y) = 0, then we can obtain y* = 0, y* = 1 and

$$x \ast = \frac{{zR_{32} - C_{22} + C_{21} - R_2}}{{z\left( {L_{21} - P_1 + P_2 + R_{33}} \right) + P_1 - R_{33}}}$$
(16)

It can be obtained from formula (16):

Proposition 2 There is a relationship between the costs difference between government active intervention and formal intervention (C21−C22) and the additional rewards obtained by government active intervention R2 and the probability of collusion: (i) \(\frac{{\partial x^ \ast }}{{\partial \left( {C_{21} - C_{22}} \right)}} > 0\), which indicates that when the costs difference between government active intervention and formal intervention are increased, the probability of collusion will increase; (ii) \(\frac{{\partial x^ \ast }}{{\partial R_2}} < 0\), which indicates that when other conditions remain unchanged, the probability of collusion will decrease when the additional rewards obtained by the active intervention of the government increase.

Further, derive for F(y), then we can obtain as follows:

$$\begin{array}{ll}F{\prime}\left( y \right) = \frac{{{\rm {d}}F\left( y \right)}}{{{\rm {d}}y}} = \left( {1 - 2y} \right)\left[ xz\left( {L_{21} - P_1 + P_2 + R_{33}} \right)\right. \\ \left. \qquad\qquad+\, x\left( {P_1 - R_{33}} \right) - zR_{33} + C_{22} - C_{21} + R_2 \right]\end{array}$$
(17)

Therefore, the evolutionary stability strategy of the government can be discussed, which is still analyzed in the following three cases.

  1. (1)

    When 0 < x = x* < 1, F(y) ≡ 0, at this time, any value of y(0 ≤ y ≤ 1)is ESS. The replicated dynamic phase diagram of the government is shown in Fig. 2a. The shaded surface in the diagram divides the strategy space into two regions, I and II, and the ESS of the government is located on the shaded surface, which indicates that when the probability of the collusion-body is a fixed value x*, although the probability of government intervention is not certain, but it is in a stable state.

    Fig. 2: Evolution phase diagram of the government strategy behavior.
    figure 2

    Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures reflect the change of the government’s strategy choice along with the change of the collusion-body’s strategy choice, where the arrow indicates the direction of the government’s strategy change.

    Full size image
  2. (2)

    When 0 < x* < x < 1, combined with the assumption P1 > R33 above, we can deduce F′(0) > 0, F′(1) < 0, at this point, y* = 1 is ESS. The corresponding replication dynamic phase diagram is shown in Fig. 2b. At this time the initial state of the government is in the strategy space I region, but it will eventually choose active intervention.

  3. (3)

    When 0 < x < x* < 1, combined with the assumption P1 > R33 above, we can deduce F′(0) < 0, F′(1) > 0, at this time, y* = 0 is ESS. The corresponding replication dynamic phase diagram is shown in Fig. 2c. At this time, the initial state of the government is in the strategy space II region, but it will eventually choose the formal intervention.

Strategic stability analysis of the public

In Eq. (12), let F(z) = 0, then we can obtain z* = 0, z* = 1 and

$$y \ast = \frac{{x\left( {R_{31} + R_{33}} \right) - C_3}}{{x\left( {R_{31} + R_{33}} \right) - R_{32}}}$$
(18)

It can be obtained from formula (18):

Proposition 3 There is a relationship between the rewards R32 given by the government to public supervision and the costs C3 of public supervision and the probability of government intervention: (i) \(\frac{{\partial y^ \ast }}{{\partial R_{32}}} < 0\), which indicates that when other conditions remain unchanged, when the public gets government rewards, the probability of government active intervention will decrease; (ii) \(\frac{{\partial y^ \ast }}{{\partial C_3}} < 0\), which indicates that when other conditions remain unchanged, when the costs of public supervision increases, the probability of government active intervention will decrease.

Further, derive for F(z), then we can obtain as follows:

$$F{\prime}\left( z \right) = \frac{{{\rm {d}}F\left( z \right)}}{{{\rm {d}}z}} = \left( {1 - 2z} \right)\left[ { - xy\left( {R_{31} + R_{33}} \right) + yR_{32} + x\left( {R_{31} + R_{33}} \right) - C_3} \right]$$
(19)

Therefore, the evolutionary stability strategy of the public can be discussed, which is still analyzed in the following three cases.

  1. (1)

    When 0 < y = y* < 1, F(z) ≡ 0, at this time, any value of z(0 ≤ z ≤ 1)is ESS. The replicated dynamic phase diagram of the public is shown in Fig. 3a. The shaded surface in the diagram divides the strategy space into two regions, I and II, and the ESS of the public is located on the shaded surface, which indicates that when the probability of active government intervention is a fixed value y*, although the probability of public supervision is uncertain, but it is in a stable state.

    Fig. 3: Evolution phase diagram of the public strategy behavior.
    figure 3

    Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures reflect the change of the public strategy choice with the change of the government strategy choice, where the arrow indicates the direction of the public strategy change.

    Full size image
  2. (2)

    When 0 < y* < y < 1, we can deduce F′(0) > 0, F′(1) < 0, at this point, y* = 1 is ESS. The corresponding replication dynamic phase diagram is shown in Fig. 3b. At this time the initial state of the public is in the strategy space I region, but it will eventually choose to participate.

  3. (3)

    When 0 < y < y* < 1, we can deduce F′(0) < 0, F′(1) > 0, at this time, y* = 0 is ESS. The corresponding replication dynamic phase diagram is shown in Fig. 3c. At this time, the initial state of the public is in the Strategy Space II region, but it will eventually choose not to participate.

Evolutionary stability analysis of the system

Based on Eq. (13), the equilibrium point of the replicated dynamic equations can be obtained (Hirsch et al., 2012). The asymptotic stability of each equilibrium point can be analyzed through the Jacobian matrix of the system (Friedman, 1991).

Let F(x) = 0, F(y) = 0, F(z) = 0, then we can get eight Pure strategy Nash equilibrium points E1(0,0,0), E2(0,0,1), E3(0,1,0), E4(0,1,1), E5(1,0,0), E6(1,0,1), E7(1,1,0) and E8(1,1,1). According to the research results of Ritzberger and Weibull (1995), it is only necessary to analyze the asymptotic stability of the above eight equilibrium points when analyzing the tripartite evolutionary game.

Based on Eq. (13), the Jacobian matrix of the system is:

$$\begin{array}{*{20}{c}} {J = \left( {\begin{array}{*{20}{c}} {\frac{{{\rm {d}}F\left( x \right)}}{{{\rm {d}}x}}} & {\frac{{{\rm {d}}F\left( x \right)}}{{{\rm {d}}y}}} & {\frac{{{\rm {d}}F\left( x \right)}}{{{\rm {d}}z}}} \\ {\frac{{{\rm {d}}F\left( y \right)}}{{{\rm {d}}x}}} & {\frac{{{\rm {d}}F\left( y \right)}}{{{\rm {d}}y}}} & {\frac{{{\rm {d}}F\left( y \right)}}{{{\rm {d}}z}}} \\ {\frac{{{\rm {d}}F\left( z \right)}}{{{\rm {d}}x}}} & {\frac{{{\rm {d}}F\left( z \right)}}{{{\rm {d}}y}}} & {\frac{{{\rm {d}}F\left( z \right)}}{{{\rm {d}}z}}} \end{array}} \right)} \\ { = \left( {\begin{array}{*{20}{c}} a & { - x\left( {x - 1} \right)\left( {z - 1} \right)\left( {L_1 + P_1 + R_{31}} \right)} & { - x\left( {x - 1} \right)\left( {y - 1} \right)\left( {L_1 + P_1 + R_{31}} \right)} \\ { - y\left( {y - 1} \right)\left[ {z\left( {L_{21} - P_1 + P_2 + R_{33}} \right) + P_1 - R_{33}} \right]} & b & { - y\left( {y - 1} \right)\left[ {x\left( {L_{21} - P_1 + P_2 + R_{33}} \right) - R_{32}} \right]} \\ { - z\left( {z - 1} \right)\left( {1 - y} \right)\left( {R_{31} + R_{33}} \right)} & { - z\left( {z - 1} \right)\left[ {x\left( {R_{31} + R_{33}} \right) - R_{32}} \right]} & c \end{array}} \right)} \end{array}$$
(20)

Among them:

$$\begin{array}{l}a = \left( {2x - 1} \right)\left[ {z\left( {1 - y} \right)\left( {L_1 + P_1 + R_{31}} \right) + y\left( {L_1 + P_1 + R_{31}} \right) + C_{11} - C_{12} - R_{12}} \right]\\ b = - \left( {2y - 1} \right)\left[ {xz\left( {L_{21} - P_1 + P_2 + R_{33}} \right) + x\left( {P_1 - R_{33}} \right) - zR_{33} + C_{22} - C_{21} + R_2} \right]\\ c = \left( {2z - 1} \right)\left[ {x\left( {y - 1} \right)\left( {R_{31} + R_{33}} \right) - yR_{32} + C_3} \right]\end{array}$$

Then the above-mentioned eight equilibrium points are substituted into the Jacobian matrix of Eq. (20) to calculate the corresponding eigenvalues, from which the strategy stability of the evolutionary game system can be analyzed and the evolutionary stability strategy of the system can be obtained. The point is asymptotically stable if and only if all three eigenvalues are <0. Table 3 shows the Jacobian matrix eigenvalues corresponding to eight equilibrium points and the asymptotic stability of equilibrium points.

Table 3 Eigenvalues and asymptotic stability of the Jacobian matrix.
Full size table

As can be seen from Table 3, the equilibrium points E1(0,0,0), E2(0,0,1) and E5(1,0,0) are not asymptotically stable, as they all have positive eigenvalues. Therefore, only E3(0,1,0), E4(0,1,1), E6(1,0,1), E7(1,1,0) and E8(1,1,1) may be the ESS of the game system. Each of these five scenarios will be discussed below in relation to Table 3. The eigenvalue λ1, λ2, λ3 represents the cost–benefit relationship among the collusion-body, the government and the public respectively. It can be seen from Table 3 that the evolutionarily stable strategy combination of this game system exists in the following five scenarios:

Scenario 1: When C12−C11 + R12 < L1 + P1 + R31, C21−C22 < R2, R32 < C3, the system has and only one evolutionary stability point E3(0,1,0), namely (not to collude, active intervention, not to participate).

Scenario 2: When C12−C11 + R12 < L1 + P1 + R31, C21−C22 < R2−C32, C3 < R32, the system has and only one evolutionary stability point E4(0,1,1), namely (not to collude, active intervention, participate). This is the ideal state of the system.

Scenario 3: When C12−C11 + R12 > L1 + P1 + R31, C21−C22 > L21 + P2 + R2−R32, the system has and only one evolutionary stability point E6(1,0,1), namely (collude, formal intervention, participate).

Scenario 4: When C12−C11 + R12 > L1 + P1 + R31, C21−C22 < P1 + R2−R33, R32 < C3, the system has and only one evolutionary stability point E7(1,1,0), namely (collude, active intervention, not to participate).

Scenario 5: When C12−C11 + R12 > L1 + P1 + R31, C21−C22 < L21 + P2 + R2−R32, C3 < R32, the system has and only one evolutionary stability point E8(1,1,1), namely (collude, active intervention, participate).

By comparing the above five situations and combining with the above hypothesis, it can be seen whether the collusion-body chooses the collusion strategy, whether the government chooses the active intervention strategy, and whether the public chooses to participate in supervision are related to their respective moral hazard and income in any situation of stable equilibrium point of system evolution.

Simulation analysis

The previous analysis theoretically studied the stability of the tripartite evolutionary game model strategy of the collusion-body, the government, and the public in major engineering construction projects. The following is a simulation analysis to verify the correctness of the theoretical analysis and investigate the evolutionary path of the strategy.

Parameter setting

Through the expert interview and combined with the actual situation, the initial values of all parameters are set as: C11 = 40, C12 = 52, C21 = 12, C22 = 4, C3 = 3, R11 = 60, R12 = 15, R2 = 10, L1 = 18, P1 = 12, R31 = 8, R32 = 2, L21 = 12, L22 = 10, P2 = 8, L3 = 10, R33 = 8, then, it is assumed that the initial probabilities of the collusion-body, the government and the public to choose different strategies are all 0.5. Variable game parameters include: the cost gap between colluding and not colluding C12−C11, the additional benefits R12 of collusive behavior, the cost gap between active intervention and formal intervention C21−C22, additional benefits R2 when the government chooses to actively intervene, cost C3 and rewards R32 of public participation in supervision. Secondly, the influences of different sets of parameters on the strategies of the tripartite evolutionary game model of collusion-body, government, and public are analyzed, and the evolutionary paths of five stable strategies are investigated in the theoretical analysis. The values of each set of parameters are given in Table 4 of “Evolutionary diagrams of game system”.

Table 4 Simulation initial parameters.
Full size table

The cost gap between colluding and not colluding, C 12−C 11 = 5,10,15,20,25,30

The evolution of the equilibrium strategy after the change of the cost gap between colluding and not colluding is shown in Fig. 4. As can be seen from Fig. 4a, there is a threshold value for (C12−C11), when it is less than this value, the evolutionary stability strategy of the system is E3(0,1,0), and with the increase of (C12−C11), the system evolves to E7(1,1,0).

Fig. 4: Parameter analysis of C12−C11, the cost gap between colluding and not colluding.
figure 4

Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures represent the case where changes in parameters C12–C11 cause changes in x, y, and z and the case where changes in C12–C11 and changes in time t cause changes in x, y, or z.

Full size image

Further, Fig. 4b–d, respectively, show the evolution trajectories of the game strategies of the collusion-body, the government, and the public over time under different (C12−C11) conditions. It can be seen from Fig. 4b that the probability of collusion-body choosing collusion is positively correlated with (C12−C11). From Fig. 4c, d, it can be seen with the increase of (C12−C11), the evolution rate of the government is getting faster and faster, while the evolution rate of the public is slowing down, but it does not change their final strategy choice.

The additional benefits of collusive behavior, R 12 = 5,10,15,20,25,30

The evolution of the equilibrium strategy after the change of the additional benefits of collusive behavior is shown in Fig. 5. It can be seen from Fig. 5a that there is a threshold for R12, when it is less than this value, the evolutionary stability strategy of the system is E3(0,1,0), and with the increase of R12, the system evolves to E7(1,1,0).

Fig. 5: Parameter analysis of R12, the cost gap between colluding and not colluding.
figure 5

Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures represent the case where changes in the parameter R12 cause changes in x, y, and z and the case where changes in R12 and changes in time t cause changes in x, y, or z.

Full size image

Further, Fig. 5b–d, respectively show the evolution trajectories of collusion-body, the government, and the public game strategies over time under different R12 conditions. It can be seen from Fig. 5b that the probability of collusion-body choosing collusion is positively correlated with R12. From Fig. 5c, d, it can be seen with the increase of R12, the evolution rate of the government becomes faster and faster, while the evolution rate of the public slows down, but it does not change their final strategy choice.

The cost gap between active intervention and formal intervention, C 21−C 22 = 5,9,10,11,12,13

The evolution of the equilibrium strategy after the change of the cost gap between active intervention and formal intervention is shown in Fig. 6. As can be seen from Fig. 6a, with other parameters unchanged, when the value of (C21−C22) is less than or equal to 9, the evolutionary stability strategy of the system is E3(0,1,0), and with the increase of (C21−C22), the system cannot reach a stable state.

Fig. 6: Parameter analysis of C21−C22, the cost gap between active intervention and formalistic intervention.
figure 6

Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures represent the case where changes in the parameter C21-C22 cause changes in x, y, and z and the case where changes in C21-C22 and changes in time t cause changes in x, y, or z.

Full size image

Further, Fig. 6b–d, respectively show the evolution trajectories of the game strategies of the collusion-body, the government, and the public over time under different (C21−C22) conditions. As can be seen from Fig. 6b, d, when the value of (C21−C22) is less than or equal to 10, the collusion-body and the public tend to choose non-collusion and non-participating supervision policies, respectively, and reach a stable state. However, with the increase of (C21−C22), the strategy selection of both of them appeared to be volatile and could not reach stability. From Fig. 6c, the probability of the government choosing the active intervention strategy is negatively correlated with (C21−C22), and the interval value of (C21−C22) affecting the government’s choice of strategy is (9,12].

Additional benefits when the government chooses to actively intervene, R 2 = 3,5,6,8,9,10

The evolution of the equilibrium strategy after the change of additional benefits R2 when the government chooses to actively intervene is shown in Fig. 7. As can be seen from Fig. 7a, when other parameters remain unchanged and the value of R2 is ≤8, there is no evolutionary stability strategy for the system, and with the increase of R2, the system gradually evolves towards E3(0,1,0) and reaches stability.

Fig. 7: Parameter analysis of R2, additional benefits when the government chooses to actively intervene.
figure 7

Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures represent the case where changes in the parameter R2 cause changes in x, y, and z and the case where changes in R2 and changes in time t cause changes in x, y, or z.

Full size image

Further, Fig. 7b–d, respectively, show the evolution tracks of collusion-body, the government, and the public game strategies over time under different R2. As can be seen from Fig. 7b, d, when the value of R2 is ≤8, the strategy choice of the collusion-body and the public oscillates, and with the increase of R2, the strategy choice of the collusion-body and the public begins to stabilize, and finally the collusion-body choose not to collude while the public also chooses not to participate in supervision. Figure 7c, it can be seen the probability of the government choosing the active intervention strategy is positively correlated with R2, and the R2 interval value affecting the government’s strategy selection is [6,9).

Cost of public participation in supervision, C 3 = 0.5,1,2,3,4,5

The evolution of the equilibrium strategy after the change of cost of public participation in supervision is shown in Fig. 8. As can be seen from Fig. 8a, there is a threshold value for C3. When it is less than this value, the evolution strategy of the system is E4(0,1,1), which is the ideal state of the system. As C3 increases, the system begins to evolve towards E3(0,1,0) and reaches stability.

Fig. 8: Parameter analysis of C3, cost of public participation in supervision.
figure 8

Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures represent the case where changes in the parameter C3 cause changes in x, y, and z and the case where changes in C3 and changes in time t cause changes in x, y, or z.

Full size image

Further, Fig. 8b–d, respectively show the evolution tracks of collusion-body, government, and public game strategies over time under different C3. It can be seen from Fig. 8b, c that the value of C3 will affect the evolution rate of the collusion-body and the government, but will not change their final strategy selection. From Fig. 8d, the probability of social public choice to participate in supervision is negatively correlated with C3, and the value of the C3 interval affecting social public strategy choice is (1,3). Therefore, the cost of public participation in supervision can be controlled within the range of <1 for achieving ideal state.

Rewards of public participation in supervision, R 32 = 2,4,6,8,10,12

The evolution of the equilibrium strategy after the change of the rewards of public participation in supervision is shown in Fig. 9. As can be seen from Fig. 9a, when R32 = 4, the evolutionary stability strategy of the system is E3(0,1,0), while with the increase of R32, the system will not be able to achieve stability.

Fig. 9: Parameter analysis of R32, rewards of public participation in supervision.
figure 9

Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures represent the case where changes in the parameter R32 cause changes in x, y, and z and the case where changes in R32 and changes in time t cause changes in x, y, or z.

Full size image

Further, Fig. 9b–d, respectively show the evolution trajectories of collusion-body, the government, and the public game strategies over time under different R32 conditions. From Fig. 9b, it can be seen when R32 is ≤4, the collusion-body will choose a non-collusion strategy, and with the increase of R32, this strategy selection will fluctuate. It can be seen from Fig. 9c that the government’s choice of active intervention strategy is negatively correlated with R32, and the interval value of R32 that affects the government’s choice of strategy is [4,8). From Fig. 9d that when R32 is ≤2, the public chooses to participate in the supervision strategy. With the increase of R32, the public’s choice of strategy fluctuates. According to the value of y*, the social public’s choice to participate in the supervision strategy is positively correlated with R32. When R32 increases to a certain threshold, the social public will choose to participate in the supervision. However, due to the parameter setting in this paper, the simulation does not reflect this conclusion.

Evolutionary diagrams of game system

Based on different sets of parameters, the simulation analysis of the tripartite evolutionary game model of the collusion-body, the government and the public are not only the verification of theoretical analysis, but also helps to intuitively understand the evolution process of the game system. Five groups of initial simulation parameters are listed in Table 4, which correspond to scenarios 1–5 in the theoretical analysis in the section “Evolutionary stability analysis of the system”.

Starting from different initial strategy combinations, the initial parameters of the five groups in Table 4 evolve 50 times over time. The simulation results are shown in Fig. 10, where Fig. 10a–e correspond to scenarios 1–5, respectively.

Fig. 10: Simulation results of game system stability evolution.
figure 10

Note: x axis, y axis, and z axis respectively represent the probabilities of collusion-body, the government, and the public choosing “collude”, “active intervention”, and “participate” strategies. These figures are the simulation results of the five evolutionary stable strategies E3(0,1,0), E4(0,1,1), E6(1,0,1), E7(1,1,0) and E8(1,1,1), indicating that no matter where the strategy of the collusion-body, the government and the public starts, it will eventually evolve to the corresponding stable strategy.

Full size image

Conclusions and management suggestions

This paper constructs the evolutionary game model of collusion-body, the government and the public by forming collusion-body with the owner, the construction party and the supervisor with certain probability, studies the decision-making behavior of each participant, discusses the stability of game strategy and carries out simulation analysis, and obtains rich conclusions, which can provide management enlightenment for the governance of collusion in mega projects.

Decision-making behavior of collusion-body and the public

The cost and benefit of collusion have an impact on the public’s decision-making behavior. On the one hand, when the owner, the construction party, and the supervisor of major engineering projects obtain more additional benefits through collusion, the probability of public participation in supervision will increase. Collusion brings more additional benefit, which will inevitably increase the collusion strength of the collusion-body. With the increase of collusion strength, the harm of collusion to major engineering construction projects increases. As the stakeholders of major engineering projects, the public will inevitably strengthen the supervision of major engineering projects. On the other hand, when the difference between the cost of non-collusion and the cost of collusion increases, the probability of public participation in supervision will increase. The non-collusion of the owner, the construction party and the supervisor of mega projects will also produce normal costs, which will not change greatly in a certain period, and the change of the difference between the non-collusion and the collusion cost is mainly caused by more cost reduction brought by the collusion. When the owner, the construction party and the supervisor collude, passive sabotage, shoddy work and jerry-cutting will occur (Yang and Du, 1996; Yan et al., 2017; Wang et al., 2022), naturally requires greater public supervision.

The decision of the public has an impact on the decision-making behavior of the collusion-body. It is found that there is a certain critical probability of public participation in supervision. When the probability of public participation in supervision is equal to the critical value, “collude” or “not to collude” is possible. But when the probability of public participation in supervision is less than the critical value, the collusion-body must choose the “collude” strategy. When the probability of public participation in supervision is greater than the critical value, the collusion-body will inevitably choose the “not to collude” strategy.

The mutual influence of collusion-body and the public on decision-making behavior brings management enlightenment. In the governance of mega projects in reality, because of its high complexity, it is often difficult to judge whether there is collusion in the project. The foregoing conclusions suggest a simple approach, focusing on whether the owner, the constructor, and the supervisor have gained additional benefits that are far less than the normal costs. In addition, the public should maintain a high-pressure supervision situation and improve the public’s willingness to supervise as much as possible, which will help the owner, the construction party and the supervisor choose not to collude.

Decision-making behavior of collusion-body and the government

The costs and benefits of the government in mega projects have an impact on the decision-making behavior of the collusion-body. The likelihood of collusion will be reduced if the government receives more additional incentives through active intervention in mega projects. The additional incentives encourage the government to intervene more actively in mega projects, which will inevitably have a deterrent effect on the possible collusive behavior of the owner, the construction party, and the supervisor, and then restrain their collusive behavior. The cost of government intervention also has an important impact on the collusive behavior of the collusion-body. The greater the difference between the cost of active intervention and the cost of formal intervention, the more likely the collusion-body are to collude, which is a very interesting conclusion. In China, active government intervention in mega projects is a matter of course, and the costs incurred are relatively stable. However, some local governments are lazy in their policies, or individual regulatory implementers go through the motions of supervision due to human relations (Le et al., 2019; Wang et al., 2022; Gao et al., 2022). In this paper, the similar formal major project intervention is called formal intervention, and the costs of formal intervention will be much smaller. The larger costs difference means that the government will be weaker in supervision, and of course, the owner, the construction party and supervisor are more likely to choose collusion behavior.

The decision of the collusion-body has an impact on the decision-making behavior of the government. It is found that the critical probability of collusion exists. When the probability of collusion is equal to the critical value, the government may intervene actively or formally. But when the probability of collusion is greater than the critical value, the government must choose to actively intervene. When the probability of collusion is less than the critical value, the government will finally choose the formal intervention strategy.

The mutual influence of the collusion-body and the government brings two aspects of management enlightenment. On the one hand, the government should appropriately increase additional incentives in mega projects. For example, increase the governing incentives, encourage the government to actively intervene in mega projects, and put an end to lazy politics; In addition, we should strengthen the supervision of government leaders in mega projects to prevent the formality and rent-seeking behavior in supervision (Li and Zhang, 2021). On the other hand, identify opportunities for active government intervention in mega projects. The conclusion shows that there is a critical probability of collusion between the owner, the construction party and the supervisor. The government should not wait until the probability of collusion is greater than the critical value to actively intervene, then the collusion-body may have completed the collusion behavior, and harm to the major project may have occurred. Therefore, the government needs to actively intervene in the initial stage of major project construction and maintain high pressure against collusion.

Decision-making behavior of the government and the public

In mega projects, the costs of public supervision and the rewards obtained by the government also have an impact on the decision-making behavior of the government. The more government rewards the public gets, the less probability the government will actively intervene in major engineering projects. By giving more rewards to the public, the government enhances the public’s willingness to participate in supervision, and the government itself takes more general intervention, thus reducing its own administrative affairs. In addition, when the costs of public participation in supervision increase, the likelihood of active government intervention decreases. The increase in the costs of public supervision indicates the high enthusiasm of the public to participate in supervision. When governments see enthusiasm for public scrutiny, they tend to do less of it themselves.

Government decisions also have an impact on public decision-making behavior. The study found that there is also a critical probability of active government intervention. When the probability of active government intervention is equal to this critical value, the public may or may not participate in supervision. But when the probability of the government’s active intervention is greater than the critical value, the public must participate in the supervision; When the probability of the government’s active intervention is less than the critical value, the public will eventually choose not to participate in the supervision.

The interaction between the government and the public is very interesting. In the construction of major engineering projects, in order to prevent the collusion of the owner, the construction party, and the supervisor, the government hopes that the public will participate more in supervision, even if it pays more incentive funds. The purpose of this is to transfer some of the supervision responsibility to the public, but the public does not necessarily “buy” (Sun and Sun, 2021). The public’s strategy is to participate in the supervision when the government actively intervenes to a certain extent, and not to participate in the supervision when the government does not actively intervene. The public chooses to “dance with the government”. The management enlightenment obtained is that the government must play a leading role in the governance of the collusive behavior of mega projects. The government must view the public supervision from the overall perspective, and the government supervision and the public supervision must promote each other. The government should not shirk its responsibilities, and it must actively intervene in mega projects to set an example for public supervision. Only in this way can the dual role of the government and the public in the governance of collusive behaviors of mega projects be fully played, which is conducive to preventing collusive behaviors and ensuring the quality of mega projects.

Decision-making behavior of collusion-body, the government, and the public

The decision-making behavior of the collusion-body, the government, and the public are in the relationship of mutual dependence and mutual influence. In the evolutionary game between the collusion-body, the government, and the public, they each have two strategies to choose from, so there is a total of eight possible evolutionary stable strategies. The conclusion of the section “Evolutionary stability analysis of the system” shows that E1(0,0,0), E2(0,0,1), and E5(1,0,0) are not asymptotically stable and therefore cannot be ESS, but E3(0,1,0), E4(0,1,1), E6(1,0,1), E7(1,1,0), and E8(1,1,1) may be ESS.

E3(0,1,0), E4(0,1,1), E6(1,0,1), E7(1,1,0), and E8(1,1,1) correspond to the strategic combinations of the five scenarios of the collusion-body, the government, and the public, respectively, which are (not to collude, active intervention, no to participate), (not to collude, active intervention, participate), (collude, formal intervention, participate), (collude, active intervention, not to participate) and (collude, active intervention, participate), the section “Evolutionary stability analysis of the system”, respectively gives the conditions for these five situations to become ESS. This paper aims to discuss the governance of collusive behavior in mega projects. Therefore, for E3(0,1,0) and E4(0,1,1), namely (not to collude, active intervention, not to participate) and (not to collude, active intervention, participate), no special attention is required. If the relevant conditions are met, as long as the government actively intervenes, no matter whether the public participates in supervision or not, the owner, the construction party, and the supervisor will not collude, which is a stable state.

We need to focus on E6(1,0,1), E7(1,1,0), and E8(1,1,1), namely (collude, formal intervention, participate), (collude, active intervention, not to participate) and (collude, active intervention, participate), and a careful analysis of them will provide more management implications. The important question is whether E6(1,0,1), E7(1,1,0), and E8(1,1,1), which have collusive strategies here, can be transformed into non-collusive strategies E3(0,1,0) and E4(0,1,1). In E6(1,0,1), that is, (collude, formal intervention, participate), can the government change from formal intervention to active intervention to transform E6(1,0,1) to E4(0,1,1)? The conclusion is uncertain, because E6(1,0,1) can also be transformed into E8(1,1,1). There is a similar situation in the transformation process from E7(1,1,0) to E4(0,1,1) by changing the state of public participation supervision. Similarly, this happens when E8(1,1,1) transitions to E3(0,1,0) by changing the state of public non-participation in supervision.

The central question is why both E3(0,1,0) and E7(1,1,0), E4(0,1,1) and E8(1,1,1) are evolutionary stable strategies. When the government is actively involved and the public does not participate in the supervision, both “collude” and “not to collude” are ESS. When the government is actively involved and the public participates in supervision, both “collude” and “not to collude” are ESS. It can be seen from the section “Evolutionary stability analysis of the system” that the establishment of each ESS needs to meet different conditions, which are caused by the different sizes of parameters such as costs, benefits, rewards, and fines of the collusion-body, the government, and the public.

By comparing the conditions for E3(0,1,0) and E7(1,1,0), E4(0,1,1), and E8(1,1,1) to become ESS, it is found that when the government changes from “formal intervention” to “active intervention”, in order to convert E6(1,0,1) to E4(0,1,1) rather than to E8(1,1,1), The costs of the collusion-body or the losses of the collusion exposure or the fines of the collusion exposure or the compensation of the collusion-body to the public must be increased, or the costs of non-collusion or the additional compensation of the collusion must be reduced. When the public changes from “not to participate” to “participate” in supervision, in order to convert E7(1,1,0) to E4(0,1,1) rather than to E8(1,1,1), it is still necessary to increase the costs or losses or fines or compensation of the collusion-body or to reduce the costs of non-collusion or additional compensation for colluding. Furthermore, by changing the relevant costs and benefits parameters, E8(1,1,1) can also evolve towards non-collusive behavior.

In general, in the game among the collusion-body, the government, and the public, if the government starts from the strategic height and takes the initiative, the governance of the collusive behavior of mega projects will achieve great results. Evolutionary stable strategy E4(0,1,1) is an ideal strategy for collusive behavior governance in mega projects. The government takes the initiative to assume the supervision responsibility, and at the same time introduces policies to encourage the public to participate in the supervision of mega projects, so as to combat the collusive behavior of the owner, the construction party, and the supervisor with the high-pressure situation of significantly increasing the collusion costs and reducing the collusion rewards. Then other evolutionary stability strategies will also be transformed into the ideal stability strategy E4(0,1,1). However, if the government does not act actively, the collusion-body, the government and the public are in a natural game state, then the governance of collusive behavior in mega projects will face huge challenges.