Introduction

Non-floodplain wetlands (NFWs) enclosed by uplands without surface runoff outlets1 provide hydrologic, biological, chemical, and ecological benefits to landscapes2,3. Thus, understanding NFW hydrologic connectivity with adjacent or distant water bodies through surface runoff or subsurface flow including groundwater (GW) is important for demonstrating their key roles in landscapes4. Water mediating the transport of matter, energy, and organisms within or between elements of the hydrologic cycle refers to hydrologic connectivity5. The degree, type, and frequency of NFW connectivity (i.e., hydrologic connectivity between NFW and other components) differ by geomorphic characteristics6. For example, surface water connectivity is prevalent in the Prairie Pothole region owing to limited underground hydraulic conductivity6, whereas GW connectivity between NFWs and other landscape components prevails on the Coastal Plain of the Chesapeake Bay Watershed (CBW)7,8.

Hydrologic connectivity between NFWs and DWs is a function of surface runoff and GW, and the major diver varies depending on the landscape and climatic characteristics1,9. Surface runoff connectivity is often measured using in-situ observations on the Coastal Plain of the CBW10,11. However, demonstrating GW connectivity using observational data is extremely challenging because of the inherent uncertainty in GW connectivity, which is characterized as a combination of nonlinear behaviors driven by interactions among climatic inputs, hydrogeologic characteristics, and human intervention3,12. Uncertainty regarding GW connectivity is further complicated by climatic seasonality (e.g., evapotranspiration [ET] and precipitation [P]). Climatic seasonality often drives landscape hydrology, leading to similar temporal dynamics of landscape components7.

On the coastal plain of the CBW, the NFW water budget increases with P and GW inflow but decreases with ET and GW outflow. When the water table is higher or lower than the bottom of NFW during the wet and dry seasons, GW inflow to and outflow from NFWs occur, respectively13. Surface inflow and outflow also affect NFW dynamics; however, the impact of surface runoff is mostly observed during heavy rainfall events7. Thus, NFW connectivity via surface water has been determined in this region after rainfall events or wet seasons10,11. In addition, NFW connectivity with DW via GW has been reported in this region, owing to subsurface permeable conditions that lead to the strong interactions between NFW and GW14,15,16,17. However, GW connectivity is speculated based on regional characteristics and the modeling approach; strong evidence in this regard is still lacking in this region.

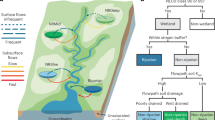
The major driving forces of the regional water budget on the CBW coastal plain are P and ET. When P is greater or lower than ET, the water budget of the landscape components, including NFWs increases or decreases, respectively. Landscape water storage is strongly dependent on wetlands in this region, which are characterized by low-gradient topography and poorly drained soils18. These conditions collectively lead to similar dynamics of NFW and DW, but their differences are observed after rainfall events for a short period7. To demonstrate GW connectivity between NFW and DW, the three components should exhibit a chain of causal relationships (represented as “cause” → “effect”) with different lag times (Fig. 1): NFW → GW with Laga, GW → DW with Lagb, and NFW → DW with Lagc. Any changes in NFWs will be reflected in GW and later in DWs along a hydrologic gradient due to lag times. A chain of causal relationships with NFW → GW and GW → DW have a direct causal relationship, while NFW indirectly affects DW. Thus, Lagc is equal to or greater than the summation of Laga and Lagb (i.e., Lagc ≥ Laga + Lagb). In contrast, the responses of NFW and DW to climatic seasonality might be simultaneous (i.e., no lag time) when the effects in both NFW and DW are linked to a shared cause (i.e., climatic seasonality). The causal relationships between NFW, GW, and DW with different lag times can be indicative of GW connectivity. Thus, identifying GW connectivity requires a metric that detects the causality between two variables with time-delayed interactions within nonlinear systems.

Figure 1
figure 1

Schematic diagram showing interactions among NFWs, GW, DW, and climatic seasonality (left) and their causal chain (right). The figure is partially adopted from Pyzoha et al.19. “A”, “B”, and “C” indicate flow from NFW to GW, GW to DW, and NFW to DW, respectively. D is a causal variable shared by NFW and DW, resulting in similar patterns. In the causal chain, Laga, Lagb, and Lagc stand for the lag for flow from NFW to GW, from GW to DW, and from NFW to DW, respectively. The figure was generated by the MS Office PowerPoint.

Full size image

Convergent cross mapping (CCM) is a novel approach for detecting causality in nonlinear systems20,21. This causal inference method is unique because it can detect causal relationships between two variables with weak or moderate coupling. CCM has been successfully tested to demonstrate causal relationships between two time-series datasets of environmental systems: temperature impacts on greenhouse gases22, invading species and soil nitrate23, between summer precipitation and aboveground biomass23, population dynamics of anchovies and sardines24, soil moisture impacts on precipitation25, hydrologic connectivity between two reservoirs26, and interactions between hydrologic and climatic variables27, and surface and groundwater relationship28. Extended CCM has also been used for distinguishing between uni- and bi-directional flow and detecting causal chains between entities with varying degrees of lagged behaviors21. Extended CCM can quantify whether two entities causally interact with each other (i.e., bi-directional) or whether only one entity affects the other entity (i.e., unidirectional)21.

In this study, we employed extended CCM to demonstrate the hydrologic connectivity of NFW with DW through GW and quantify the time delay in this causal relationships in the Greensboro watershed (GBW) within CBW in the USA7. We speculated that if NFW has any hydrologic connectivity with DW via GW, the following would be observed from CCM analysis: (1) two direct causality (NFW → GW and GW → DW) and one indirect causality (NFW → DW) would be present; (2) the opposite direction of causality would not appear, and (3) direct causality would have shorter lag time than indirect causality. Because of the high uncertainty in the causation between GW and DW, we considered pseudo DW (DWadj) adjacent to the DW located at the outlet of the watershed, including the NFW (DWorg). It was also assumed that causality would be observed between NFW and DWorg but not between NFW and DWadj.

Materials and methods

Study area and data

The NFW is located within the GBW, which is the drainage area of the U.S. Geological Survey (USGS) gauge station #01491000, on the coastal plain of the CBW (Fig. 2). The CBW is divided into 11 hydrogeomorphic regions (HGMRs) based on the rock type and physiographic province17. The study area is included in the coastal plain upland (CPU) with high precipitation infiltration into shallow aquifer due to well-drained soils and flat topography17. The CPU is also underlaid with unconsolidated sediments with high permeability, leading to large groundwater discharge to streams17.

Figure 2
figure 2

The spatial location of the studied wetland. CBW indicates the chesapeake bay watershed. GBW (Greensboro watershed) and TCW (Tuckahoe Creek watershed) are the drainage areas of the USGS gauge stations #01491000 and #01491500, respectively. NHD stands for the National Hydrography Dataset. The location of well and piezometer was further zoomed-in in Fig. S1 of the Supplementary Material and the data source used in this figure is listed in Table S1 of the Supplementary Material. The description of the hydrogeomorphic region (HGMR) is available in Table S2 of the Supplementary Material. The map was generated by ArcMap 10.7.

Full size image

The sizes of NFW and its drainage area are 1 ha and 3.1 ha, respectively; and the drainage area is dominated by forest7. The nearest streams indicated by the USGS high-resolution National Hydrography Dataset (NHD) is 0.1 km from NFW (Fig. 2). The “Wetland” component of the U.S. Department of Agriculture Conservation Effects Assessment Project (CEAP‐Wetlands) implemented a well and piezometer to explore the surface water level and groundwater level of NFW in this region, respectively29. A PVC pipe with a 2.54 cm diameter was utilized to construct a well and piezometer, with well screens being positioned over the whole length of the wells and the lower 30 cm of the piezometers. The well was utilized to directly measure the height of the water column, whereas the piezometer was employed to assess the pressure of the groundwater exerted by the water column. The well was equipped with pressure transducers (Campbell Scientific CS451, Campbell Scientific, Logan, Utah, United States), while the piezometer was physically linked to the data logger (Campbell Scientific CR1000). To see the interactions between the surface and groundwater, a well and piezometer were installed side by side (Fig. S1 of the Supplementary Material) since different soil conditions under the bottom of NFW might not correctly capture their interactions30.

The studied NFW was monitored from January 2016 to December 2019 (Table 1). The water levels were continuously collected by a well and piezometer at every 15-min, respectively (Fig. 2). The well and piezometer in the NFW was installed to 0.9 and 3.0 m below the wetland bottom, respectively, and they were spatially close each other30. Following similar previous studies7,30, this study assumed the water levels monitored by a well and piezometer indicated NFW and GW, respectively.

Table 1 Descriptions of the studied NFW and its monitoring.
Full size table

Baseflow from streamflow collected from the USGS gauge station was used to represent DWorg, and USGS gauge station #01491500 was also prepared for DWadj (Fig. 2). Both DWorg and DWadj were spatially adjacent, and thus they similarly responded to regional climatic seasonality. DWorg was hydrologically downstream of NFW based on the watershed boundary. Baseflow separation was calculated using the EcoHydRology package31 in the R programming environment. The digital filter separation described by Nathan and McMahon32 was used in this package, and the default settings were applied in our study.

15-min data were aggregated into daily values for the CCM analysis. The NFW measurements included 177 missing samples (January 11th–July 6th, 2017), and data incompleteness could cause errors in the CCM analysis. The missing samples were filled with simulations from the process-based model developed to predict the water level of NFW33. The process-based model was modified to simulate the hydrology of NFW, and the model successfully predicted the daily water level of the NFW studied with high accuracy with the R2 value of 0.84–0.88 and further detailed results are provided in Junyu et al.33.

Convergent cross mapping

In this study, we introduced CCM, a method suggested by Sugihara et al.20 and extended by Ye et al.21, to detect causal relationships between variables of interest. CCM is a handy and robust numerical tool to determine causal influence when the time series of two variables are available. The theoretical basis of this approach comes from Takens’ theorem: when “x” (cause) influences “y” (effect) in dynamical systems, the value of “x” can be retrieved from the value of “y”. One critical process is to determine whether the accuracy of the reconstruction of “x” from “y” increases as the number of L (library vectors) of “y” increases. As the number of L means the number of different time points used for the reconstruction. In other words, it tests whether the inclusion of “y” values from longer periods reconstructs “x” better. The degree of how accurately “y” estimates “x”, called cross map skill (p), is determined based on Pearson’s correlation between observed and estimated “x”20. Most importantly, this test allows screening of spurious correlational relationships. If “x” and “y” have a spurious correlational relationship, an increase in L does not result in a more accurate reconstruction of “x”, because the correlation is only due to the short-time synchronization of the two variables. In CCM, this relationship between x and y is represented as “y xmap x” that means x is estimated from y. In this study, we stated “y (effect) xmap x (cause)” as “x → (affects) y” to better indicate the relationship between cause and effect. This study also tested the significance of CCM results (p-value < 0.01) to identify spurious causation using the method introduced in Bonotto et al.28 and Ye et al.34. The test included assessing whether the cross-map skill at full library size is significantly greater than the highest lagged cross-correlation and surrogate time series. The p-value was computed as below:

$$p{\text{-}}value=(n+1)/(k+1),$$
(1)

where k is the total number of surrogates and n is the number of replicates with greater cross-map skill than the actual value.

The extension and enhancement of CCM by Ye et al.34 solved one of the weaknesses of the original version: overwhelming influence from “x” on “y” may lead to successful CCM in both directions (meaning that “y” also affects “x”), although this is not the case. This weakness, called ‘generalized synchrony,’ occurs when “y” is almost only affected by “x”, and thus, “x” and “y” act as one system. To address this issue, Ye et al.34 considered different lag times. Causal relationships signify that there exists a chronological order between the two variables. Therefore, if the causal relationship between “x” and “y” is unidirectional (here only “x” affects “y”), the lag time found in CCM recreating “x” from “y” will be negative, while the time lag found in CCM recreating “y” from “x” will be positive. The optimal time lag is decided when the cross map skill is largest. The negative optimal lag time of “x (cause)” → “y (effect)” indicates the response of “y” to any changes in “x” will appear after the optimal lag time. The zero optimal lag time of “x → y” denotes “y” promptly responds to “x” without any lag time, and the positive optimal lag time of “x → y” means “x (cause)” responds to “y (effect)” with the lag time, indicating illogical causation.

We used the rEDM package developed by Ye et al.34 to implement CCM processes in R. The processes involved the reconstruction of individual system states using a time series to generate the joint state, for the estimation of one variable from another. Individual system states were reconstructed by the time-delay embedding approach, which represents the delay coordinates of each system state. The optimal embedding dimension (E) of each system state was calculated through the rEDM package in R34.

Results

Temporal dynamics of non-floodplain wetland (NFW), groundwater (GW), and downstream water (DW)

The daily time series of NFW, GW, DWorg, and DWadj are shown in Fig. 3a,b. Overall, the temporal dynamics of NFW, GW, DWorg, and DWadj were highly similar in response to the seasonal trends of this area, with high and low water balance during the winter and summer seasons, respectively. NFW and GW ranged from − 0.9 to 0.4 m and from − 1.4 to 0.3 m, respectively, while the variation ranges of DWorg and DWadj were 2–403 (m3/s) and 15–195 (m3/s), respectively. DWorg and DWadj showed similar temporal dynamics (Fig. 3b). Monthly variations in ET were high during summer months (June, July, and August) and low during winter months (December, January, and February) and the monthly pattern of precipitation was overall uniform over the course of the year, indicating seasonality in this region (Fig. 3c,d).

Figure 3
figure 3

(a) Daily time series of non-floodplain wetlands (NFW) and groundwater (GW), (b) daily time series of two downstream waters (DWs), (c) monthly time series of evapotranspiration (ET), and (d) monthly time series of precipitation. The yellow-green line in (a) indicates the predicted NFW by the process-based model33. DWorg and DWadj are baseflow derived from streamflow measured at USGS gauge stations #01491000 and #01491500, respectively. The figure was generated by the R 3.6.1 program.

Full size image

NFW and GW dynamics did not comply with several peaks of DW owing to the vertical limits in the monitoring range of NFW and GW (dotted vertical purple arrows in Fig. 3b). When the water storage of NFW was filled by heavy rainfall, the fill-spill dynamics of NFW frequently occurred10,11. Regarding the configuration of a well and piezometer (Fig. S2 of the Supplementary Material) the maximum upper water level of NFW and GW is the same as the depth of the NFW while the monitoring range of DW had no limit, leading to different dynamics between NFW/GW and DW. The monitoring lower limit also caused the flat level of NFW during the summer of 2019 (dotted vertical purple arrow in Fig. 3a). In addition, DW is the summation of intra-watershed processes and thus the behavior of DW might be different from NFW and GW that are the tiny landscape component.

Embedding dimension and nonlinearity

To apply the CCM method, the embedding dimension (E) should be determined. The embedding dimension (E) is the number of time steps used for the prediction. Following previous studies, the optimal E values for NFW, GW, and DW were computed using a simplex projection (Table 2)24,25. Nonlinearity was identified by observing the best prediction when different combinations of the degree of nonlinearity (θ) and embedding dimension (E) were tested. When the best prediction was shown with θ > 0, the time-series variable was nonlinear. The nonlinearity was assessed by S-map with the embedding dimension (E, 1, 2,…, 10) and the degree of nonlinearity (θ, 0, 0.25, 0.5,…, 0).

Table 2 The optimal embedding dimensions (E) and degree of nonlinearity (θ) of time-series observations.
Full size table

Differentiation of causation from non-causal relationships

In the CCM method, we attempted to differentiate causation from non-causal correlations between observed and estimated variables: NFW → GW, GW → DW, and NFW → DW, using cross map skill. Figure 4 shows the cross map skill (p) between the observed and estimated variables with different library lengths (L). Interestingly, overall relationships had high cross map skill (p) with a longer library length (L) with the significant results (p-value < 0.01). The causality was detected at NFW → GW, which was driven by the vertical water flow from surface to groundwater. The high cross map skill (p) of GW → NFW was likely due to the seasonal flow from upland to NFW via GW in this region7. The causality results between precipitation and hydrologic variables (e.g., NFW, GW, and DWorg) showed precipitation exhibited a causal relationship with three hydrologic variables (p-value < 0.01, Fig. S3 of the Supplementary Material). This finding suggested that the seasonal lateral movement of GW to NFW could be substantiated by the causative link between precipitation and these hydrologic variables.

Figure 4
figure 4

Cross map skill (p) of observed and estimated values as a function of the length of the library (L): (a) NFW and GW, (b) GW and DWorg, (c) NFW and DWorg, (d) GW and DWadj, and (e) GW and DWadj. The dotted horizontal line is the highest lagged cross-correlation. x → y indicates x affects y. NFW and GW indicate non-floodplain wetland and groundwater, respectively. DWorg and DWadj are baseflow derived from streamflow measured at USGS gauge stations #01491000 and #01491500, respectively. The figure was generated by the R 3.6.1 program.

Full size image

However, the significant test showed that the cross map skill of GW → NFW at full library size was lower than the highest lagged cross-correlation, indicating non-causation (Fig. 4a). The cross map skill (p) of GW → DWorg and DWadj was high and remained unchanged regardless of the length of the library (L). DWorg and DWadj represents the combination results of hydrological landscape components. A tiny component (GW) could have minimal impacts on DWorg and DWadj and thus the cross map skill (p) of GW → DWorg and DWadj did not consistently increase with an increase in the length of the library (L). In contrast, DWorg and DWadj complied with seasonal dynamics indicated by dominant driving forces (e.g., P and ET), leading to a relatively high value of the cross map skill (p) of DWorg and DWadj → NFW/GW7. Except for GW → NFW, all interactions were statistically significant.

Detecting causality in the hydrological connectivity between NFW, GW, and DW

First, we applied extended CCM method to further identify the true causality among NFW, GW, DWorg and DWadj. The true causations in Fig. 4 were further explored. Figure 5a shows that the optimal cross map lags of NFW → GW was not distinguishable from zero lag time. This was likely because the spatial configuration of the well and piezometer might lead to synchronization between NFW and GW. In addition, daily measurements might not capture lagged responses of GW to NFW.

Figure 5
figure 5

Cross map skill (p) with cross map lag between: (a) NFW and GW, (b) GW and DWorg, (c) NFW and DWorg, (d) GW and DWadj, and (e) GW and DWadj. x → y indicates x affects y. NFW and GW indicate non-floodplain wetland and groundwater, respectively. DWorg and DWadj are baseflow derived from streamflow measured at USGS gauge stations #01491000 and #01491500, respectively. The figure was generated by the R 3.6.1 program.

Full size image

The optimal lag time of GW → DWorg was observed at a negative one day (Fig. 5b), indicating that changes in GW would be reflected in DWorg one day later. Non-causation with the positive optimal lag time was found in the opposite direction (DWorg → GW). The optimal lag time of NFW → DWorg was negative 3 days, and the opposite direction was zero (Fig. 5c). The results of NFW → DWorg informed that after 3 days, any changes in NFW would affect DWorg. Regarding the lag time in the causal chain of NFW, GW, and DWorg, the CCM results represented changes in NFW caused changes in GW and then subsequently affected DWorg. The lag times of among NFW, GW, and DWorg agreed with our assumption as the sum of the lag times of two direct causal links (NFW → GW and GW → DWorg) was lower than the indirect causal link (the optimal lag of NFW → DWorg). Moreover, the two lagged interactions (GW → DWorg and NFW → DWorg) were found to be statistically significant (p-value < 0.01). Regarding the optimal lag times, the significance of two causal links (GW at t → DWorg at t + 1 and NFW at t → DWorg at t + 3, where t represents the time) were assessed using the method proposed by Bonotto et al.28 and Ye et al.34. The results from extended CCM well demonstrated the causal chain from NFW to DWorg via GW with different lag times.

In the case of GW → DWadj, the optimal lag time was a positive one day, representing that DWadj responded to GW although any changes did not take place at GW (Fig. 5d). The optimal lag time of DWadj → GW with the positive optimal lag time also showed non-causation. Interestingly, a negative one day was the optimal lag time of NFW → DWadj, indicating the changes in NFW will be reflected in DWadj after one day. Regarding a transitive causal chain from NFW to DW through GW, the negative one-day optimal lag time of NFW → DWadj could not support the GW hydrologic connectivity between NFW and DWadj because GW was not causal to DWadj (Fig. 5e). Therefore, the extended CCM analysis showed that the evidence of causal relationships in a transitive causal chain from NFW to DW through GW was only found at DWorg and not at DWadj based on the lagged responses among them.

Discussions and limitations

In this study, CCM was used to find causal relationships in nonlinear dynamical systems for observables with weak or moderate coupling. Previous studies explored various causal relationships between two entities in environmental systems using CCM22,23,24,25,26,27,28. Among them, different causal methods including CCM were compared for the hydrologic variable26,27,28. A study by Bonotto et al.28 tested the impacts of data seasonality, sampling frequency, and long-term trends on the performance of CCM. Following previous studies, this study could provide additional insight on the use of CCM on the causality between one small casual variable (i.e., NFW) and an aggregated affected-variable (i.e., DW). NFW is one of water storages that drains to DW known as the summation of intra-watershed processes, and thus NFW might have trivial impacts on DW. To partially address the uncertainty on the causal impacts of NFW on DW, this study introduced pseudo DW to demonstrate the reliability of CCM results. This method could offer the potential way of using CCM to see causality between a small causal variable and the aggregated-affected variable. However, the observed causal relationship between NFW and DW was uncertain although this study adopted pseudo DW to partially address this issue. Extensive observations along the hydraulic gradient from NFW to DW might offer reliable evidence of causation, but this is challenging. To achieve dependable causality, efforts to install multiple observations along a hydrologic gradient between NFW and DW would be critical.

This study used daily time series of NFW, GW and DW mainly due to missing data in NFW (see the green line in Fig. 3a). In-situ observational data from a well and piezometer inevitably includes missing data due to uncontrollable environment conditions. The CCM results with daily time series represented the synchronized behaviors between NFW and GW (Fig. 5a), but sub-daily time series might show the lagged interaction between NFW and GW. The CCM analysis could not be performed with missing data. Accordingly, 15-min monitoring data were converted into daily data to replace missing data by the simulations from a process-based model that demonstrated decent performance measures in this region33. The process-based model only simulated daily dynamics of NFW33. Sub-daily observations data are recommended to see lagged responses of GW to NFW since the CCM results were sensitive to the sampling frequency28.

To test the influence of sampling frequency on CCM results, this study applied a conversion process that transformed daily data into 3-day and 7-day intervals through the averaging of daily values (Fig. 6). Despite variations in sampling frequency, the overall trends remained consistent. The highest lagged cross-correlation, represented by the dotted horizontal line, tended to increase as the temporal frequency decreased from 1 to 7 days. Notably, the causal link between NFW and GW exhibited significance with one-day data but did not show significance with 7-day data. This discrepancy was attributed to the lower cross-map skill at the full library size, which fell below the highest lagged cross-correlation (Fig. 6f). This observation suggests that the causal interaction between NFW and GW might not be effectively captured by CCM when utilizing 7-day data, as their interactions are subtle and low-frequency data fails to depict their causal behaviors. The conversion of data from higher to lower frequencies likely resulted in smoother data patterns, allowing for the generalization of subtle behaviors observed in individual NFWs.

Figure 6
figure 6

Cross map skill (p) of observed and estimated values as a function of the length of the library (L) with 3-day (a–e) and 7-day (f–j) data. The figure was generated by the R 3.6.1 program.

Full size image

The spatial configuration of a well and piezometer also likely led to synchronization between NFW and GW (Fig. 5a). If a piezometer was distant to a well, the lagged response of GW to NFW might be observed. However, the subsurface soil characteristic greatly affected the vertical water transport from NFW to GW30. When groundwater flow direction was not clear, measurements from a piezometer might not be associated with those from a well away from a piezometer. Thus, implementing a piezometer at the spot distant to a well is challenging. Although NFW and GW were monitored at the same spot with different vertical ranges, that practices might be the best option to see hydrologic interactions of NFW with sub-surface systems.

Using pseudo DW (represented as DWadj), this study showed a transitive causal chain from NFW to DW via GW in this region. The two direct causations (NFW → GW and GW → DWorg) had a shorter lag time than one indirect causation (NFW → DWorg), but the one direct causation (GW → DWorg) showed a lower correlation than indirect one (NFW → DWorg). Extended CCM method emphasized a direct causation with shorter lag times and stronger correlation than an indirection one21. However, our results were not consistent with the previous study21. It was speculated that: (1) a lower correlation in direction causation was likely due to the monitoring spot of GW spatially far away from DW; and (2) the two entities (NFW and DWorg) in indirect causality were directly exposure to driving forces and their behaviors might have great similarity while GW indirectly affected by driving forces could have less similarity.

In this region, the nutrient transport time via GW ranged from years to decades and this time varied by subsurface conditions35. Our results estimated a 3-day lag time from NFW to DW via GW, which is not in agreement with a previous study35. This could be explained by “old” water in long-term groundwater storage36,37. The streamflow is mainly comprised of baseflow derived from long-term groundwater storage (“old” water), and the “new” precipitation has strong impacts on streamflow at storm events36. The water vertical transport from NFWs to GW is the pressure head of the groundwater storage, sequentially pushing the old water from upgradient to downstream and eventually releasing “old” water closer to streamflow. As groundwater storage is influenced by various landscape components, the analysis of a 3-day lag time using only the concept of “old” water may not be adequately comprehensive. The cumulative effects of multiple landscape elements on downstream water through groundwater could lead to an extended lag time for indirect causation, compared to the total of the lag times for two direct causations. More accurate estimation of lag time would be possible using tracers38 and extensive monitoring stations. This study is the first attempt to corroborate GW hydrologic connectivity between NFW and DW using CCM with available monitoring data and showed causal signals. This finding would provide insight on the role and NFW at a watershed. As emphasized by Bonotto et al.28, environmental monitoring data are often limited and thus the interpretation of CCM results should be performed with detailed observations.

Conclusions

Our study applied a causal inference method (CCM) to detect causality between NFW and DW through GW on the Coastal Plain of the CBW. The hydrologic connectivity of NFW with DW via surface runoff was often observed, but demonstrating the connectivity via GW is difficult because strong climatic seasonality causes all landscape components have similar behaviors. CCM could detect causality among variables in nonlinear dynamical systems using time-series observations. Using CCM, we examined the causal relationship between NFW and DW via GW using daily time series. The CCM results showed a transitive causal chain from NFW to DW through GW with shorter lag of direct causation (NFW → GW and GW → DW) relative to indirect causation (NFW → DW). However, this causal chain was not observed with pseudo DW. These results support the notion that NFW is hydrologically connected with DW through GW. These findings emphasize the important role and benefits of NFW in landscape hydrology.