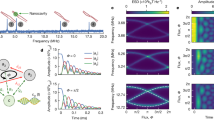
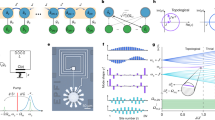
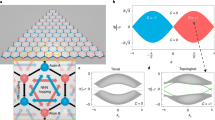
Abstract
The fermionic Kitaev chain is a canonical model featuring topological Majorana zero modes1. We report the experimental realization of its bosonic analogue2 in a nano-optomechanical network, in which the parametric interactions induce beam-splitter coupling and two-mode squeezing among the nanomechanical modes, analogous to hopping and p-wave pairing in the fermionic case, respectively. This specific structure gives rise to a set of extraordinary phenomena in the bosonic dynamics and transport. We observe quadrature-dependent chiral amplification, exponential scaling of the gain with system size and strong sensitivity to boundary conditions. All these are linked to the unique non-Hermitian topological nature of the bosonic Kitaev chain. We probe the topological phase transition and uncover a rich dynamical phase diagram by controlling interaction phases and amplitudes. Finally, we present an experimental demonstration of an exponentially enhanced response to a small perturbation3,4. These results represent the demonstration of a new synthetic phase of matter whose bosonic dynamics do not have fermionic parallels, and we have established a powerful system for studying non-Hermitian topology and its applications for signal manipulation and sensing.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data in this study are available from the Zenodo repository at https://doi.org/10.5281/zenodo.10279485.
References
Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys.-Usp. 44, 131–136 (2001).
McDonald, A., Pereg-Barnea, T. & Clerk, A. A. Phase-dependent chiral transport and effective non-Hermitian dynamics in a bosonic Kitaev–Majorana chain. Phys. Rev. X 8, 041031 (2018).
Budich, J. C. & Bergholtz, E. J. Non-Hermitian topological sensors. Phys. Rev. Lett. 125, 180403 (2020).
McDonald, A. & Clerk, A. A. Exponentially-enhanced quantum sensing with non-Hermitian lattice dynamics. Nat. Commun. 11, 5382 (2020).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Ma, G., Xiao, M. & Chan, C. T. Topological phases in acoustic and mechanical systems. Nat. Rev. Phys. 1, 281–294 (2019).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Bergholtz, E. J., Budich, J. C. & Kunst, F. K. Exceptional topology of non-Hermitian systems. Rev. Mod. Phys. 93, 015005 (2021).
Ding, K., Fang, C. & Ma, G. Non-Hermitian topology and exceptional-point geometries. Nat. Rev. Phys. 4, 745–760 (2022).
Gong, Z. et al. Topological phases of non-Hermitian systems. Phys. Rev. X 8, 031079 (2018).
Kawabata, K., Shiozaki, K., Ueda, M. & Sato, M. Symmetry and topology in non-Hermitian physics. Phys. Rev. X 9, 041015 (2019).
Peano, V., Houde, M., Marquardt, F. & Clerk, A. A. Topological quantum fluctuations and traveling wave amplifiers. Phys. Rev. X 6, 041026 (2016).
Bandres, M. A. et al. Topological insulator laser: experiments. Science 359, 4005 (2018).
Yao, S. & Wang, Z. Edge states and topological invariants of non-Hermitian systems. Phys. Rev. Lett. 121, 086803 (2018).
Kunst, F. K., Edvardsson, E., Budich, J. C. & Bergholtz, E. J. Biorthogonal bulk–boundary correspondence in non-Hermitian systems. Phys. Rev. Lett. 121, 026808 (2018).
Martinez Alvarez, V. M., Barrios Vargas, J. E. & Foa Torres, L. E. F. Non-Hermitian robust edge states in one dimension: anomalous localization and eigenspace condensation at exceptional points. Phys. Rev. B 97, 121401 (2018).
Okuma, N., Kawabata, K., Shiozaki, K. & Sato, M. Topological origin of non-Hermitian skin effects. Phys. Rev. Lett. 124, 086801 (2020).
Zhang, K., Yang, Z. & Fang, C. Correspondence between winding numbers and skin modes in non-Hermitian systems. Phys. Rev. Lett. 125, 126402 (2020).
Ghatak, A., Brandenbourger, M., Wezel, J. & Coulais, C. Observation of non-Hermitian topology and its bulk-edge correspondence in an active mechanical metamaterial. Proc. Natl Acad. Sci. USA 117, 29561–29568 (2020).
Helbig, T. et al. Generalized bulk–boundary correspondence in non-Hermitian topolectrical circuits. Nat. Phys. 16, 747–750 (2020).
Weidemann, S. et al. Topological funneling of light. Science 368, 311–314 (2020).
Xiao, L. et al. Non-Hermitian bulk–boundary correspondence in quantum dynamics. Nat. Phys. 16, 761–766 (2020).
Liang, Q. et al. Dynamic signatures of non-Hermitian skin effect and topology in ultracold atoms. Phys. Rev. Lett. 129, 070401 (2022).
Zhang, L. et al. Acoustic non-Hermitian skin effect from twisted winding topology. Nat. Commun. 12, 6297 (2021).
Wang, K. et al. Generating arbitrary topological windings of a non-Hermitian band. Science 371, 1240–1245 (2021).
Chen, C.-W. et al. Mechanical analogue of a Majorana bound state. Adv. Mater. 31, 1904386 (2019).
Qian, K. et al. Observation of Majorana-like bound states in metamaterial-based Kitaev chain analogs. Phys. Rev. Res. 5, 012012 (2023).
Wanjura, C. C., Brunelli, M. & Nunnenkamp, A. Topological framework for directional amplification in driven-dissipative cavity arrays. Nat. Commun. 11, 3149 (2020).
Yokomizo, K. & Murakami, S. Non-Bloch band theory in bosonic Bogoliubov–de Dennes systems. Phys. Rev. B 103, 165123 (2021).
Flynn, V. P., Cobanera, E. & Viola, L. Topology by dissipation: Majorana bosons in metastable quadratic Markovian dynamics. Phys. Rev. Lett. 127, 245701 (2021).
Mathew, J. P., Pino, J. & Verhagen, E. Synthetic gauge fields for phonon transport in a nano-optomechanical system. Nat. Nanotechnol. 15, 198–202 (2018).
Pino, J., Slim, J. J. & Verhagen, E. Non-Hermitian chiral phononics through optomechanically-induced squeezing. Nature 606, 82–87 (2021).
Wanjura, C. C. et al. Quadrature nonreciprocity in bosonic networks without breaking time-reversal symmetry. Nat. Phys. 19, 1429–1436 (2023).
Metelmann, A. & Clerk, A. A. Nonreciprocal photon transmission and amplification via reservoir engineering. Phys. Rev. X 5, 021025 (2015).
Hatano, N. & Nelson, D. R. Vortex pinning and non-Hermitian quantum mechanics. Phys. Rev. B 56, 8651–8673 (1997).
Xiong, Y. Why does bulk boundary correspondence fail in some non-Hermitian topological models. J. Phys. Commun. 2, 035043 (2018).
Coulais, C., Fleury, R. & Wezel, J. Topology and broken hermiticity. Nat. Phys. 17, 9–13 (2021).
Brunelli, M., Wanjura, C. C. & Nunnenkamp, A. Restoration of the non-Hermitian bulk–boundary correspondence via topological amplification. SciPost Phys. 15, 173 (2022).
Porras, D. & Fernández-Lorenzo, S. Topological amplification in photonic lattices. Phys. Rev. Lett. 122, 143901 (2019).
Wanjura, C. C., Brunelli, M. & Nunnenkamp, A. Correspondence between non-Hermitian topology and directional amplification in the presence of disorder. Phys. Rev. Lett. 127, 213601 (2021).
Wan, L.-L. & Lü, X.-Y. Quantum-squeezing-induced point-gap topology and skin effect. Phys. Rev. Lett. 130, 203605 (2023).
Yuan, H. et al. Non-Hermitian topolectrical circuit sensor with high sensitivity. Adv. Sci. 10, 2301128 (2023).
Parto, M., Leefmans, C., Williams, J. & Marandi, A. Enhanced sensitivity via non-Hermitian topology. Preprint at arxiv.org/abs/2305.03282 (2023).
Könye, V. et al. Non-Hermitian topological ohmmeter. Preprint at arxiv.org/abs/2308.11367 (2023).
Bardyn, C. E. & Imamoglu, A. Majorana-like modes of light in a one-dimensional array of nonlinear cavities. Phys. Rev. Lett. 109, 253606 (2012).
Barlas, Y. & Prodan, E. Topological braiding of non-Abelian midgap defects in classical metamaterials. Phys. Rev. Lett. 124, 146801 (2020).
Patil, Y. S. S. et al. Measuring the knot of non-Hermitian degeneracies and non-commuting braids. Nature 607, 271–275 (2022).
Lee, G., Jin, T., Wang, Y.-X., McDonald, A. & Clerk, A. Entanglement phase transition due to reciprocity breaking without measurement or post-selection. PRX Quantum 5, 010313 (2023).
Busnaina, J. H. et al. Quantum simulation of the bosonic Kitaev chain. Preprint at https://arxiv.org/abs/2309.06178 (2023).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Weaver, M. J. et al. Coherent optomechanical state transfer between disparate mechanical resonators. Nat. Commun. 8, 824 (2017).
Shkarin, A. B. et al. Optically mediated hybridization between two mechanical modes. Phys. Rev. Lett. 112, 013602 (2014).
Meystre, P. & Sargent, M. Elements of Quantum Optics 4th edn (Springer, 2007).
Acknowledgements
We acknowledge A. A. Clerk for discussions. M.B. acknowledges funding from the Swiss National Science Foundation (Grant No. PCEFP2_194268). J.d.P. acknowledges financial support from the ETH Fellowship programme (Grant No. 20-2 FEL-66). This work is part of the research programme of the Netherlands Organisation for Scientific Research. It is supported by the European Research Council (Starting Grant No. 759644-TOPP).
Author information
Authors and Affiliations
Contributions
J.J.S. and E.V. conceived the project. J.J.S. fabricated the sample, developed the experimental methods, performed the experiments and analysed the data. C.C.W., M.B., J.d.P. and A.N. developed the theory with input from J.J.S. and E.V. All authors contributed to the interpretation of the results and writing the manuscript. E.V. and A.N. supervised the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Xin-You Lü, Weijian Chen and Haitan Xu for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Topological phase diagrams for varying chain lengths.
These panels show the calculated end-to-end gain \({\chi }_{{x}_{1}\to {x}_{N}}\) for finite open chains of length N = 4 (panel (a), corresponding to Fig. 3c), N = 10 (b), and N = 20 (c), as a function of phase φ and squeezing amplitude λ/J for J/γ = 5/16. As in Fig. 3c, the dashed lines depict the phase boundaries, determined by the structure (point gap and winding of origin) of the complex spectrum for an infinite chain under PBC. We recognize that the conditions for which the end-to-end gain exceeds unity align closely with the topological phase boundary that marks spectral winding of the origin. Slight deviations between those two are observed for smaller chains near φ = 0 and φ = π/2, and are thus associated with finite size effects. Still, the general structure of the phase diagram of the infinite chain is clearly recognized in the end-to-end gain for N = 4.
Extended Data Fig. 2 Experimental frequency accuracy.
(a) Thermomechanical reference spectra. Before each experimental run, a set of thermomechanical spectra is taken, with modulations off, to determine the value of the mechanical resonance frequencies ωj. A typical set is shown. Spectra are averaged over 50 runs and fitted by a Lorentzian function, with uncertainty (standard deviation) in the extracted ωj’s (grey dashed lines) between σω,fit/(2π) = 20 − 24 Hz, estimated from the fit residuals. (b) Frequency stability of the mechanical modes. Resonator frequencies ωj are extracted from thermomechanical resonance spectra, measured repeatedly over a duration of 90s. Error bars denote the ± 2σ fit uncertainty interval estimated from residuals. Over time, fluctuations in ωj are observed with standard deviation σω,fluct/(2π) = 43 − 64 Hz, depending on the mode. Correlated fluctuations across the modes indicate a common origin, that we attribute to fluctuations in the optical spring effect. This is compatible with the observation that mechanical modes with higher index and lower optomechanical couplings g0,j experience smaller frequency fluctuations.
Extended Data Fig. 3 Bar chart depiction of response matrices.
(a) Bar chart representation of the susceptibility matrices \({(\gamma {\chi }_{jk})}^{2}/4\) plotted in Fig. 1d, for G = 0.75, G = 1.0, and G = 1.25. (b) The same data as in (a), depicted in a basis of rotated quadratures chosen to numerically minimize the weight of the off-diagonal blocks. The close correspondence between (a) and (b) illustrates that the original (unrotated) calibration of quadratures was performed accurately, and represents the quadrature sensitivity of the response optimally.
Extended Data Fig. 4 Inferred experimental dynamical matrices.
The dynamical matrix \({{\mathcal{M}}}_{a}\) describing the evolution of mode operators \({a}_{j},{a}_{j}^{\dagger }\) is inferred from the measured susceptibility matrix χ through \({{\mathcal{M}}}_{a}={{\mathcal{T}}}^{-1}{({\rm{i}}\chi )}^{-1}{\mathcal{T}}\), where \({\mathcal{T}}\) is the matrix that transforms from mode basis \(\{{a}_{j},{a}_{j}^{\dagger }\}\) to the quadrature basis {xj, pj}. A perfect bosonic Kitaev chain has purely imaginary \({{\mathcal{M}}}_{a}\), that is, no on-site detunings and purely imaginary coupling rates. In our experiments, the real part of the diagonal elements of \({{\mathcal{M}}}_{a}\) indicates a small residual detuning (averaged across the four participating modes) of 3%, 5% and 7% of the mechanical linewidth γ for G = 0.75, 1, 1.25, respectively. The first two modes have higher optomechanical couplings g0 and are therefore more susceptible to fluctuations and nonlinearities in the optical spring effect.
Supplementary information
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Slim, J.J., Wanjura, C.C., Brunelli, M. et al. Optomechanical realization of the bosonic Kitaev chain. Nature 627, 767–771 (2024). https://doi.org/10.1038/s41586-024-07174-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-024-07174-w
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.