Quantum Kibble–Zurek mechanism and critical dynamics on a programmable Rydberg simulator

Abstract

Quantum phase transitions (QPTs) involve transformations between different states of matter that are driven by quantum fluctuations¹. These fluctuations play a dominant part in the quantum critical region surrounding the transition point, where the dynamics is governed by the universal properties associated with the QPT. Although time-dependent phenomena associated with classical, thermally driven phase transitions have been extensively studied in systems ranging from the early Universe to Bose–Einstein condensates^2,3,4,5, understanding critical real-time dynamics in isolated, non-equilibrium quantum systems remains a challenge⁶. Here we use a Rydberg atom quantum simulator with programmable interactions to study the quantum critical dynamics associated with several distinct QPTs. By studying the growth of spatial correlations when crossing the QPT, we experimentally verify the quantum Kibble–Zurek mechanism (QKZM)^7,8,9 for an Ising-type QPT, explore scaling universality and observe corrections beyond QKZM predictions. This approach is subsequently used to measure the critical exponents associated with chiral clock models^10,11, providing new insights into exotic systems that were not previously understood and opening the door to precision studies of critical phenomena, simulations of lattice gauge theories^12,13 and applications to quantum optimization^14,15.

Main

The Kibble–Zurek mechanism^2,3, which describes nonequilibrium dynamics and the formation of topological defects in a second-order phase transition driven by thermal fluctuations, has been verified experimentally in a wide variety of physical systems^4,5. Recently, the concepts underlying the Kibble–Zurek description have been extended to the quantum regime^7,8,9. Here, the typical size of the correlated regions, ξ, after a dynamical sweep across the QPT scales as a power law of the sweep rate, s, with an exponent μ determined entirely by the QPT’s universality class. Specifically, QKZM postulates that when the timescale over which the Hamiltonian changes becomes faster than the characteristic response time, τ, which is determined by the inverse of the energy gap between the ground and excited states, nonadiabatic excitations prevent the continued growth of correlated regions (Fig. 1a, b). The resulting scaling exponent, μ = ν/(1 + νz), is determined by a combination of the critical exponent, ν, which characterizes the divergent correlation length, and the dynamical critical exponent z, which characterizes the relative scaling of space and time close to the critical point¹. Although QKZM has many important implications—for example, in quantum information science¹⁴—its experimental verification is challenging owing to the coupling of many-body systems to the environment¹⁵. Recently, experimental control over isolated quantum systems enabled the observation of scaling behaviour across QPTs described by mean-field theories^16,17. Although important aspects of QPTs have already been explored in strongly correlated systems¹⁸, experimental observation of quantum critical phenomena beyond mean-field approximations in real-time dynamics remains a challenge^15,19,20.

Fig. 1: Quantum Kibble–Zurek mechanism and phase diagram.

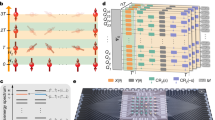
a, Illustration of the QKZM. As the control parameter approaches its critical value, the response time, τ, which is given by the inverse energy gap of the system, diverges. b, When the temporal distance to the critical point becomes equal to the response time, as marked by the red crosses in a, the correlation length, ξ, stops growing owing to nonadiabatic excitations. c, Numerically calculated ground-state phase diagram. Circles (diamonds) denote numerically obtained points along the phase boundaries, calculated using (infinite-size) density-matrix renormalization group techniques (Methods). The shaded regions are guides for the eye. Dashed lines show the experimental trajectories across the phase transitions determined by the pulse diagram (inset). d, Measured density–density Rydberg correlations (circles) with fits to the expected ordered pattern (solid lines), consistent with ${{\mathbb{Z}}}_{4}$- (orange), ${{\mathbb{Z}}}_{3}$- (purple) and ${{\mathbb{Z}}}_{2}$-ordered (green) states. Error bars denote the standard error of the mean (s.e.m.) and are smaller than the marker size.

We investigate quantum criticality using a reconfigurable one-dimensional array of  ⁸⁷Rb atoms with programmable interactions²¹. In our system, 51 atoms in the electronic ground state $\left|g\right\rangle$, which are evenly separated by a controllable distance, are homogeneously coupled to the excited Rydberg state $\left|r\right\rangle$, in which they experience van der Waals interactions with a strength that decays as V(r) ∝ 1/r⁶, where r is the interatomic distance. This system is described by the many-body Hamiltonian,

$$\frac{{\mathscr{H}}}{\hbar }=\frac{\Omega }{2}\sum _{i}\left(\left|{g}_{i}\right\rangle \left\langle {r}_{i}\right|+\left|{r}_{i}\right\rangle \left\langle {g}_{i}\right|\right)-\Delta \sum _{i}{n}_{i}+\sum _{i < j}{V}_{ij}{n}_{i}{n}_{j}$$

(1)

where ${n}_{i}=\left|{r}_{i}\right\rangle \left\langle {r}_{i}\right|$ is the projector onto the Rydberg state at site i, Δ and Ω are the detuning and Rabi frequency of the coherent laser coupling between $\left|g\right\rangle$ and $\left|r\right\rangle$, respectively, V_ij is the interaction strength between atoms in the Rydberg state at sites i and j, and ħ is the reduced Planck constant. For negative values of Δ, the many-body ground state corresponds to a state in which all atoms are in the electronic ground state $\left|g\right\rangle$, up to quantum fluctuations, and belongs to a so-called ‘disordered’ phase with no broken spatial symmetry. For Δ > 0, several spatially ordered phases arise from the competition between the detuning term, which favours a large Rydberg fraction, and the Rydberg blockade, which prohibits simultaneous excitation of atoms separated by a distance smaller than the blockade radius, R_b, defined by V(R_b) ≡ Ω. As illustrated in Fig. 1c, d, we probe different QPTs into states breaking various symmetries by choosing the interatomic spacing and sweeping the control parameter, Δ, across the phase boundary.

We first focus on the QPT into the antiferromagnetic phase with broken ${{\mathbb{Z}}}_{2}$ symmetry, which is known to belong to the Ising universality class¹. Using an interatomic spacing, a, such that R_b/a ≈ 1.69, we create an array of 51 atoms in the electronic ground state and slowly turn on Ω at Δ < 0, adiabatically preparing the system in the ground state of the disordered phase. We then increase the detuning at a constant rate, s, up to a final value Δ_f, at which point we slowly turn off Ω (see inset of Fig. 1c) and measure the state of every atom. We examine the dynamical development of correlations between the atoms, characterized by the Rydberg density–density correlation function:

$$G(r)=\sum _{i}\left(\left\langle {n}_{i}{n}_{i+r}\right\rangle -\left\langle {n}_{i}\right\rangle \left\langle {n}_{i+r}\right\rangle \right)/{N}_{r}$$

(2)

where the normalization factor N_r is the number of pairs of sites separated by distance r. By fitting an exponential decay to the modulus of the correlation function, we extract the correlation length. The experimental results show growth of the correlation length as the detuning approaches the critical point, followed by saturation once the detuning is swept past the critical point into the ordered phase (Fig. 2b). From the individual images it is apparent that, whereas for fast sweeps the ordered domains are frequently interrupted by defects (domain walls), for slow ramps considerably longer domains are observed (Fig. 2a). A systematic analysis of the final correlation lengths after crossing into the ordered phase shows that a power-law scaling model ξ(s) = ξ₀(s₀/s)^μ with μ = 0.50(3), where the uncertainty represents one standard deviation, describes our measurements accurately (Fig. 2c). These results are consistent with numerical simulations (red points) of the coherent evolution of the system using matrix product states (MPS).

Fig. 2: QKZM for a QPT into the ${{\mathbb{Z}}}_{2}$-ordered phase.

a, Single-shot images of the atom array before and after a fast (orange arrow) and a slow (blue arrow) sweep across the phase transition, showing larger average sizes of correlated domains for the slower sweep. Green spots (open circles) represent atoms in $\left|g\right\rangle$ $\left(\left|r\right\rangle \right)$. Blue rectangles mark the position of domain walls, and the red and grey coloured regions highlight the extent of the correlated domains. b, Correlation length growth and saturation as the system crosses the QPT at different rates. The grey dashed line indicates the critical detuning. c, Experimental (green) and MPS-simulated results (red) for the dependence of the correlation length on the inverse sweep rate across the phase transition. The length is extracted from fitting the modulus of the correlation data to an exponential decay. Error bars denote fit uncertainty. The dashed line indicates a power-law fit to the experimental results with a scaling exponent of μ = 0.50(3).

The QPT into the ${{\mathbb{Z}}}_{2}$-ordered phase is in the Ising universality class¹, with critical exponents in one dimension of z = 1, ν = 1 and, consequently, μ_Ising = 0.5. Our observations are consistent with these quantitative predictions and are distinct from those associated with a mean-field Ising transition, which are described^1,16 by z = 1, ν = 1/2 and yield μ_mf = 1/3. These results offer the first experimental verification of the QKZM in an isolated quantum system that defies a mean-field description.

A key concept associated with critical phenomena is that of universality, which is manifested by the collapse of correlations to a universal form when rescaled according to the corresponding critical exponents¹. Such a signature is a strong test of an underlying universal scaling law and, in connection with the QKZM, should appear upon rescaling lengths²² by (s/s₀)^μ. Figure 3a shows that the rescaled correlations for R_b/a ≈ 1.81 indeed collapse onto two smooth branches, which in turn collapse on top of each other when the correlations are rectified as (−1)^rG(r) (inset in Fig. 3a), according to the ${{\mathbb{Z}}}_{2}$-order parameter.

Fig. 3: Universality of spatial correlations.

a, c, Collapse of the measured (a) and numerically calculated (c) correlations in the ${{\mathbb{Z}}}_{2}$-ordered phase, with distances rescaled according to the extracted scaling exponents. The purple line connects the points of the correlation function that correspond to the slowest sweep rate. The insets show the staggered rescaled correlations. The negative values of the correlation function indicate nontrivial correlations between domain walls. b, d, Collapse of the measured (b) and numerically calculated (d) correlations in the ${{\mathbb{Z}}}_{3}$-ordered phase, highlighting the energetic difference of the different types of defect, as shown by the distinguishability of the two negative branches, that is, a deviation from a period-3 density wave. All error bars indicate the s.e.m.

While the QKZM is a coarse-grained description that predicts the mean density of defects, the shape of the correlation function gives further access to microscopic details of the system. Detailed inspection of the rescaled correlation functions reveals nontrivial deviations from a simple exponential decay. In particular, the correlations in Fig. 3a become negative for a range of distances, which implies complex dynamics in the formation and spreading of defects. The observed corrections to simple QKZM predictions are consistent with recent theoretical analyses^22,23 and are in good agreement with numerical simulations using MPS (Fig. 3c). Finally, applying the universal rescaling to the correlation growth shown in Fig. 2b enables us to independently estimate the values of critical exponents (Extended Data Fig. 7), showing that our results are consistent with z = ν = 1, which is associated with the Ising QPT.

Having established the validity of the QKZM—as well as its limitations—for a QPT in the Ising universality class, we now explore transitions into more complex ${{\mathbb{Z}}}_{N}$-ordered phases, where Rydberg excitations are evenly separated by N > 2 sites (see Fig. 1c). The correlation functions at smaller interatomic spacings after slow detuning sweeps reflect the spatial ordering of the ${{\mathbb{Z}}}_{3}$- and ${{\mathbb{Z}}}_{4}$-ordered phases (Fig. 1d). In addition, we determine the probability of finding two Rydberg excitations separated by N sites for each value of N and R_b (Fig. 4b). By combining these measurements with the numerically obtained critical points (see Fig. 1c), we experimentally identify approximate boundaries for the regions that are consistent with the ${{\mathbb{Z}}}_{2}$-, ${{\mathbb{Z}}}_{3}$- and ${{\mathbb{Z}}}_{4}$-ordered phases in Fig. 4b. Within these regions, the dominant type of order is the one associated with the corresponding phase, whereas the second most prevalent type of order arises from the lowest-energy (most probable) defects. In particular, we observe that in the ${{\mathbb{Z}}}_{3}$-ordered phase, the most likely type of defect changes from ${{\mathbb{Z}}}_{2}$-like (for smaller values of R_b/a) to ${{\mathbb{Z}}}_{4}$-like as R_b/a increases.

Fig. 4: Power-law scaling for different interactions.

a, Experimental realization of the CCM²⁵. The top row shows a single fluorescence image of a state in the ${{\mathbb{Z}}}_{3}$-symmetry-broken phase (R_b/a ≈ 2.16), with four ${{\mathbb{Z}}}_{2}$-type defects displacing the Rydberg atoms in one direction (anticlockwise chirality). The bottom rows display a system with stronger interactions (R_b/a ≈ 2.43), in which ${{\mathbb{Z}}}_{4}$-type defects are favoured and the Rydberg atoms are displaced in the opposite direction (clockwise chirality). The coloured regions highlight the extent of the correlated domains, which are labelled by clock orientations in connection to the CCM. b, Fraction of the final state consistent with the different ${{\mathbb{Z}}}_{N}$-ordered states observed in the experiment (left, circles) and in numerical simulations (right, diamonds). Within the ${{\mathbb{Z}}}_{3}$-ordered region, the most dominant type of defect changes from ${{\mathbb{Z}}}_{2}$- to ${{\mathbb{Z}}}_{4}$-type as the interaction range increases. The higher contrast in the calculated domain probabilities in Fig. 4b is due to finite detection fidelity, which does not affect the extracted value of μ. c, Scaling exponent, μ, as a function of R_b/a, obtained from experimental data (left, circles) and MPS simulations (right, diamonds). Pale-blue points indicate instances in which the measured correlation lengths do not grow beyond the size of R_b/a. Shaded areas indicate regions consistent with ${{\mathbb{Z}}}_{2}$- (green), ${{\mathbb{Z}}}_{3}$- (purple) and ${{\mathbb{Z}}}_{4}$-ordered (orange) phases. The solid green line corresponds to μ_Ising, the purple dashed lines represent the upper²⁵ and lower²⁶ bounds of μ_CCM, and the purple dotted line denotes the value of μ_CCM obtained from the best numerical estimates of z (ref. ²⁵) and ν (ref. ²⁷). Error bars represent the 68% confidence interval (b) and one standard deviation of the power-law fit (c), which is dominated by systematic effects in the extraction of individual correlation lengths.

We test for a power-law scaling behaviour of the correlation length growth as a function of ramp speed at different interaction strengths (Fig. 4c). To compare the results for all interaction strengths consistently, we fit the correlation function to an exponentially decaying density wave with a period set by the underlying order (as opposed to the modulus of the correlation function used in Fig. 2c). The scaling is extracted through a power-law fit to the resulting correlation lengths. In parameter regimes far from regions of competing order, we observe three stable plateaus for the regions consistent with ${{\mathbb{Z}}}_{2}$, ${{\mathbb{Z}}}_{3}$ and ${{\mathbb{Z}}}_{4}$ order. For interaction strengths at which there is a strong competition between different types of order, we do not observe the formation of long-range correlations (pale-blue points in Fig. 4c). In these cases, the detuning sweeps either do not fully cross the phase boundary into the ordered phases (Methods) or potentially enter theoretically predicted incommensurate phases^11,24.

To understand these observations, we compare them to finite-size scaling analyses of ground-state properties^25,26,27, as well as MPS-based numerical simulations of our experimental protocol for the full Hamiltonian (equation (1)). For the transitions into the ${{\mathbb{Z}}}_{2}$-ordered phase, some of the extracted values of μ are slightly larger than the exponent expected from the Ising model, μ_Ising = 0.5. We attribute these deviations to a combination of long-ranged interactions, of finite-size and/or time effects, and of systematic effects related to the inversion of the alternating pattern (Fig. 3a, c; see also Methods).

QPTs associated with the breaking of a ${{\mathbb{Z}}}_{3}$ symmetry are more complex owing to competition between the different types of defects that can be formed. In our system, the defects correspond to two different types of domain walls, in which the distance between neighbouring Rydberg excitations is two and four sites (see Fig. 4a). For experimentally accessible parameter regimes, the different associated excitation energies generally lead to an asymmetry between these defects (see also Fig. 4b). Correspondingly, the ${{\mathbb{Z}}}_{3}$-symmetry breaking is believed to be in the universality class of the three-state chiral clock model (CCM) (see Fig. 4a, Methods and ref. ²⁵).

The exact nature of such phase transitions has been a subject of intense theoretical research for the past three decades^{10,11,25,26,27,28}. Only very recently, numerical studies of equilibrium scaling properties^25,26,27 provided evidence for a direct transition²⁷ along some paths across the phase boundary, where the expected range of values of the scaling exponent is μ_CCM < 0.45 (ref. ²⁵) and μ_CCM > 0.25 (ref. ²⁶). Our experimental results are consistent with a direct CCM phase transition over a range of interaction strengths with μ ≈ 0.38, in agreement with the theoretical value obtained by combining the results of the most extensive numerical finite-size scaling studies^25,27 (dashed line in Fig. 4c). Further evidence for a direct chiral QPT is provided by the universal scaling behaviour into the ${{\mathbb{Z}}}_{3}$-ordered phase (see Fig. 3b, d).

The transition into the ${{\mathbb{Z}}}_{4}$-ordered phase is even more involved. At present, complete understanding of this transition is lacking owing to the potential presence of an intermediate gapless incommensurate phase^11,28. Our experimental results in this region are reasonably consistent with power-law scaling with μ ≈ 0.25. Although recent theoretical work shows that QKZM scaling may still hold on quenching through a gapless phase, albeit with a modified (system-specific) power-law exponent²⁹, detailed theoretical understanding of our experimentally observed exponents in the ${{\mathbb{Z}}}_{4}$ regime requires further studies.

Detailed comparison of our experimental results across all phases with the numerical simulation of the Hamiltonian dynamics using MPS are presented in Fig. 4. Although qualitatively similar, the datasets display clear discrepancies. The most important one is a systematic offset between the extracted values of μ from the experiment, finite-size scaling analysis and time-dependent MPS simulations. Although it can be potentially attributed to experimental imperfections and subtle differences between the experimental system and the model used for the numerical simulations (see Methods), the disagreement of the MPS simulation with both the experimental results and the finite-size scaling analyses of equilibrium properties highlights the difficulty in approximately modelling complex nonequilibrium dynamics of many-body systems.

Our observations demonstrate a new approach for investigating quantum critical phenomena and provide insights into the physics of exotic QPTs that do not lend themselves to simple theoretical analyses. Increasing the system size, improving the atomic coherence properties and exploring wider parameter regimes may allow more precise probing of exotic QPTs into both ordered and incommensurate phases^11,24,25,27 in various models. In particular, the present approach is well suited for simulations of lattice gauge theories¹³. Whereas the system studied here is formally equivalent to a quantum link model on a ladder geometry³⁰, two- and three-dimensional systems realized using novel trapping techniques^31,32 can be used to simulate a wide variety of non-trivial lattice gauge models¹². Finally, the methods demonstrated in this work can be used to effectively encode and explore solutions to computationally difficult combinatorial optimization problems, such as finding the maximum independent set³³. Detailed understanding of quantum dynamics in such systems might have direct application to exploring quantum speedup in both adiabatic and dynamical quantum optimization algorithms¹⁴.

Methods

Rydberg array preparation

The experiment uses an acousto-optic deflector to generate multiple optical tweezers, which are loaded probabilistically from a cold gas of ⁸⁷Rb atoms in a magneto-optical trap. Each tweezer can be loaded with up to a single atom. Once the cloud is dispersed, a fluorescence image, similar to the ones shown in Fig. 2a, is taken to identify loaded traps. The traps are then rearranged to generate a defect-free regular array of 51 atoms that are evenly separated by distance³⁴ a.

We define our spin Hamiltonian according to two pseudospin-1/2 states. The first is a ground-state hyperfine sublevel, $\left|g\right\rangle =\left|5{S}_{1/2},F=2,{m}_{F}=-2\right\rangle$, and the second is the interacting Rydberg state $\left|r\right\rangle =\left|70S,J=1/2,{m}_{J}=-1/2\right\rangle$, where F, m_F and J, m_J are the hyperfine and total angular momentum quantum numbers, respectively. These two states are coupled by a two-photon process via the intermediate state $\left|e\right\rangle =\left|6{P}_{3/2},F=3,{m}_{F}=-3\right\rangle$. The two lasers operate at wavelengths of 420 nm for the lower transition and 1,013 nm for the upper transition.

The 420-nm laser is a frequency-doubled titanium–sapphire laser (SolsTiS 4000 PSX F by M Squared) locked to an optical reference cavity (ATF- 6010-4 from Stable Laser Systems). The 1,013-nm laser is an external-cavity diode laser (CEL002 by MOGLabs) that is locked to the same reference cavity. The light transmitted through the cavity is used to injection-lock another 1,013-nm laser diode, which is then amplified by a tapered amplifier³⁵. Both beams are focused along the array axis (aligned with the quantization axis) to drive σ⁻ and σ⁺ transitions for the 420-nm and 1,013-nm beams, respectively.

Pulse generation

We modulate the 420-nm Rydberg laser with an acousto-optic modulator (AOM) driven by an arbitrary waveform generator (AWG; M4i.6631-x8 by Spectrum Instrumentation). For each experiment, we program a waveform with varying amplitudes, frequencies and phases in the time domain into the AWG, which is then transmitted to the AOM through a high-power radiofrequency amplifier (ZHL-1-2W+ by Mini-Circuits).

The nonlinear AOM response to changes in amplitude and frequency poses a technical challenge. The deflection efficiency is not proportional to the waveform amplitude, and large changes in the latter lead to variations in the former. These effects lead to distortions in the pulse shape. We apply feed-forward corrections to the amplitude to match the output intensity to the desired waveform amplitude, as well as to compensate for the variations with frequency.

Pulse parameters

All pulses begin by turning on the value of Ω linearly over 1 μs at a fixed initial detuning Δ₀. We select our initial detuning to be as close to the critical point as possible and subject to the constraint that the initial turn-on is still fully adiabatic. We identify this detuning experimentally by ramping Ω on and then off for various fixed detunings. In the adiabatic case, all the atoms should return to $\left|g\right\rangle$. We therefore select the detuning closest to resonance that shows no excess excitation at the end of the pulse. For a typical measurement in the ${{\mathbb{Z}}}_{2}$ regime, we select Δ₀ = −2.5 MHz (Extended Data Fig. 1).

The final detunings of the sweeps are chosen in most cases to cross the tip of the corresponding phase boundary. In some cases in which the interaction strength is on the border between two phases, we do not fully cross over the boundary (Extended Data Fig. 2a).

The power-law scaling behaviour of the correlation length can be limited owing to strong nonadiabaticity far from the critical point, where the behaviour of the system is susceptible to microscopic details and is expected to deviate from universal theories, limiting the speed of the sweeps across the phase transition. At the same time, slow sweeps are more susceptible to decoherence, both because of the longer pulse time window and because the system remains closer to the ground state near the critical point and the growing quantum correlations are increasingly sensitive to environmental noise. To determine the range of rates for which QKZM scaling can be observed, we perform a sweep into each of the ordered phases at a wide range of sweep speeds s. We fit the correlation lengths for each parameter, discarding all the instances in which the correlation length is smaller than the size of the blockade radius, with a model that accounts for incoherent processes as saturation in the final size of the correlation length, namely:

$$\xi (s)=\left(\begin{array}{cc}{\xi }_{0}{({s}_{0}/s)}^{\mu } & s\le {s}_{{\rm{c}}}\\ {\xi }_{0}{({s}_{0}/{s}_{{\rm{c}}})}^{\mu } & s > {s}_{{\rm{c}}}\end{array}\right.$$

(3)

From this fit, we set s_min > s_c and find s_max such that ξ(s_max) > R_b (an example is shown in Extended Data Fig. 3). In this way, we determine the sweep parameters for the different values of the interaction strength (see Extended Data Table 1).

Numerical computation of the phase diagram

The quantum critical points along the phase boundary on the phase diagram presented in the main text were obtained using both finite- and infinite-system density-matrix renormalization group (DMRG) algorithms^{36,37,38,39,40,41}. The filled coloured regions in Fig. 1c are not the result of numerical simulations and only show the expected shape of the phases approximately. In this section, we describe the details of the DMRG calculations.

For the infinite-system DMRG (iDMRG), we generally follow the method summarized in ref. ⁴², in which translationally invariant matrix product states (iMPS) are used as variational ansatze for ground-state wavefunctions. Our Hamiltonian with long-range interactions is encoded using matrix product operator representations, where 1/r⁶-decaying interactions are approximated by a linear combination of four exponentials:

$$\frac{1}{{r}^{6}}\approx \sum _{i=1}^{4}{c}_{i}{x}_{i}^{r}$$

(4)

with (c₁, c₂, c₃, c₄) = (170.55, 1.29, 0.0252, 0.000279) and (x₁, x₂, x₃, x₄) = (0.00519, 0.0835, 0.279, 0.565)⁴³. The resulting function provides an excellent approximation with relative error less than 10⁻⁵ (Extended Data Fig. 4). This accuracy implies that even with the strongest interaction strength probed in our experiments (R_b ≈ 3.5), the maximum correction, ${V}_{0}\left|\left(1/{r}^{6}\right)-{\sum }_{i=1}^{4}{c}_{i}{x}_{i}^{r}\right|\lesssim (2{\rm{\pi }})\times 36{\rm{kHz}}$, is much weaker than the smallest energy scale that can be probed within our experimental timescales.

Our phase diagram involves quantum phases that spontaneously break spatial translation symmetry. Hence, it is important that the number of spins in a translationally invariant unit cell of our iMPS ansatz must be compatible with the broken spatial symmetry. We use two or six spins as a unit cell to probe phase transitions from disordered to ${{\mathbb{Z}}}_{2}$-ordered or ${{\mathbb{Z}}}_{3}$-ordered phases, respectively. Incommensurate phases or onset of spatial symmetry breaking that is not compatible with the number of spins per unit cell can be identified by oscillatory behaviour of wavefunction overlaps or energy densities over iterations.

To obtain the ground-state wavefunction, we iteratively optimize iMPS tensors until the (local) overlap between wavefunctions from two consecutive optimization steps approaches unity up to a small error ε. As convergence criteria, we require that either ε ≤ 10⁻⁸ or ε is limited by truncation errors arising from a finite bond dimension⁴², D. We use a wide range of bond dimensions up to D = 200, depending on the quantity of interest to be computed and on the convergence of the wavefunctions. For example, computing the ground-state energy density is relatively insensitive to bond dimensions, whereas extracting correlation lengths near the critical point requires a substantially larger D.

We thus extract the phase boundaries from the energy density. Specifically, we use iDMRG to extract the ground-state energy density ${\mathscr{E}}$ along a line in the parameter space, (R_b/a, Δ/Ω), and compute its second derivative along the line. When crossing a QPT, the second-order derivative of the energy density exhibits a sharp feature. For example, Extended Data Fig. 2b shows the numerically computed energy densities per unit cell (six spins) as a function of R_b/a ∈ [1.75, 2.25] for a fixed Δ/Ω = 2 with D = 10. We find clear cusps at R_b/a ≈ 1.86 and 2.18, corresponding to critical points from ${{\mathbb{Z}}}_{2}$-ordered to disordered and to ${{\mathbb{Z}}}_{3}$-ordered phases. Similar procedures along different lines lead to the phase diagram in Extended Data Fig. 2a and in Fig. 1c.

These phase boundaries are also reproduced using finite-system DMRG^44,45 with a bond dimension of up to D = 60 for a chain of L = 51 atoms and open boundary conditions. The first three energy levels are individually targeted, which in turn gives us access to the energy gap. The closing of the gap outlines well-defined lobes in the phase diagram, the boundaries of which overlap well with the points extracted previously with iDMRG (Extended Data Fig. 5).

A few remarks are in order. First, it has been previously discussed that the ${{\mathbb{Z}}}_{3}$-ordered phase may be interfacing incommensurate phases²⁴. However, we do not find any evidence of incommensurate phases between ${{\mathbb{Z}}}_{2}$ and ${{\mathbb{Z}}}_{3}$ phases with up to Δ/Ω = 12 within our numerical precision. The nature of the direct transition from disordered to ${{\mathbb{Z}}}_{3}$-ordered phases is discussed in refs ^25,26,27. Second, we have not explicitly identified the phase transition between disordered to ${{\mathbb{Z}}}_{4}$-ordered phases. This is because our choices of a unit cell (two or six spins) are not compatible with ${{\mathbb{Z}}}_{4}$-ordered wavefunctions. Instead, the boundary of the disordered phase for R_b/a > 3 (yellow diamonds in Extended Data Fig. 2a) has been extracted from the convergence of the iDMRG algorithm; as Δ/Ω increases with a fixed R_b/a, the yellow diamonds in Extended Data Fig. 2a indicate the points at which the iDMRG algorithm ceases to converge and instead exhibits oscillatory behaviours. Our method does not distinguish whether this is due to the onset of the ${{\mathbb{Z}}}_{4}$-ordered phase or to a gapless incommensurate phase.

Extraction and scaling of correlation length

From the fluorescence images obtained at the end of an experimental sequence, we calculate the two-dimensional Rydberg density–density correlation map:

$$G(i,j)=\langle {n}_{i}{n}_{j}\rangle -\langle {n}_{i}\rangle \langle {n}_{j}\rangle $$

(5)

To minimize boundary effects, we disregard eight sites from each edge. From the remaining bulk correlations, we average out this map over diagonal lines of constant |i − j| to obtain the Rydberg density–density correlation described in equation (2) (Extended Data Fig. 6). The uncertainties on the values of G(r) are found via jackknife analysis.

Two different approaches are used to extract a characteristic length from such correlations. For transitions into ${{\mathbb{Z}}}_{N}$-ordered states (Fig. 4), we perform a least-squares fit to the data with the model function:

$$\hat{G}(r)=A{{\rm{e}}}^{-r/\xi }{\hat{G}}_{N}{(r)}_{{\rm{gs}}}$$

(6)

where A is the amplitude at r = 0, ξ is the correlation length and ${\hat{G}}_{N}{(r)}_{{\rm{gs}}}$ is the ideal correlation function at integer values of r for the corresponding ${{\mathbb{Z}}}_{N}$-ordered state, with a peak every N sites:

$$\begin{array}{l}{\hat{G}}_{2}{(r)}_{{\rm{g}}s}=cos(2{\rm{\pi }}r/2)\\ {\hat{G}}_{3}{(r)}_{{\rm{g}}s}=cos(2{\rm{\pi }}r/3)\\ {\hat{G}}_{4}{(r)}_{{\rm{g}}s}=cos(2{\rm{\pi }}r/4)+(1/2)cos(2{\rm{\pi }}r/2)\end{array}$$

(7)

The range of distances used for all fits is 0 < r ≤ 20, where the cutoff at 20 sites is used to avoid any potential finite-size effects of the system.

In addition to the procedure described above, for ${{\mathbb{Z}}}_{2}$-ordered states it is possible to extract a correlation length by fitting an exponential decay to the modulus of the correlation function, as is done in Fig. 2. This method enables the determination of the correlation length in a way that is less susceptible to systematic effects arising from inversions of the alternating pattern, as observed in Fig. 3a. However, this method cannot be applied to ${{\mathbb{Z}}}_{N}$-ordered states for N > 2, necessitating the use of a more general approach, such as the function $\hat{G}(r)$ defined above. Whereas the scaling exponents extracted using both of these methods for the ${{\mathbb{Z}}}_{2}$-ordered-state data are consistent within error bars, $\hat{G}(r)$ is used to obtain all exponents in Fig. 4c.

To extract the most likely scaling exponent μ at a given interaction, we fit the data with a power law

$$\xi ={\xi }_{0}{(s/{s}_{0})}^{-\mu }$$

(8)

where s is the detuning sweep rate.

${{\mathbb{Z}}}_{N}$ domain density

In the fluorescence images obtained at the end of each experimental sequence, we identify the loss of an atom to a Rydberg excitation. In this way, we can directly count the number of instances of two lost atoms separated by N sites, with every site in between containing an atom. To extract the data for Fig. 4b, we disregard the first eight sites from the edges and count the instances in which both ends of the N atom chain are within the bulk, f_N. The relative probability for two lost atoms separated by N sites is given by:

$${p}_{N}=\frac{N\times {f}_{N}}{{\sum }_{i > 0}(i\times {f}_{i})}$$

(9)

Unlike G(r), p_N is susceptible to detection infidelity^21,35.

Length rescaling of correlation functions

In Fig. 3, we use the normalized measured density–density correlation functions, $\frac{1}{{A}_{i}}G{(r)}_{i}$, and rescale the length r by the QKZM length-scaling exponent found via the scaling analysis of the correlation length, r → (s/s₀)^μr.

Finite-time scaling

The length-scaling exponent, μ, found experimentally sets constraints to the possible combinations of the critical exponents z and ν at a given interaction strength. To estimate, or qualitatively test, the possible values of z and ν, given the constraints set by μ, we make use of the fact that in the critical region, all system properties scale in a universal way. The QKZM predicts a universal scaling of time with a scaling exponent of zν/(1 + zν), in addition to the scaling of length⁴⁶ with μ = ν/(1 + zν). In the experiment, the control parameter used to cross the QPT is δ = Δ−Δ_c, where Δ_c is the value of the detuning at the critical point and can be estimated through numerical simulations (see section ‘Numerical computation of the phase diagram’). Near the critical point, the control parameter varies in time as δ(t) = st, leading to a universal scaling of δ(s) = δ₀(s₀/s)^κ, where κ = −1/(1 + zν). Using the data shown in Fig. 2 for the correlation length growth across the transition into the ${{\mathbb{Z}}}_{2}$-ordered phase, we can apply the transformation ξ → ξ(s/s₀)^μ and δ → δ(s/s₀)^κ to observe how well the data collapse to a universal shape. Extended Data Fig. 7 shows that these data are consistent with having critical exponents z = 1 ≈ ν, as expected for the Ising universality class.

Numerical simulation of Kibble–Zurek dynamics

We model the dynamics of the system numerically using MPS and use a variant of a time-evolving block decimation algorithm to propagate the state. We use a state update that allows us to include exactly the effect of the interaction between atoms that are separated by less than $\ell =7$ sites. Interactions beyond this range are neglected. To this end, we use a trotterization for the unitary that propagates the system from a time t_k to a time t_k+1 = t_k + Δt as

$$U({t}_{k}\to {t}_{k+1})\approx \prod _{p=1}^{N-\ell }exp\left(-i{h}_{p}({t}_{k}){\rm{\Delta }}t\right)$$

(10)

where

$${h}_{p}({t}_{k})=\frac{1}{\ell }\sum _{j=0}^{\ell -1}\left(\frac{\Omega ({t}_{k})}{2}{\sigma }_{p+j}^{x}-\Delta ({t}_{k}){n}_{p+j}\right)+\sum _{i=0}^{\ell -2}\sum _{j=i+1}^{\ell -1}\frac{1}{\ell -(j-i)}{V}_{i,j}{n}_{p+i}{n}_{p+j}$$

(11)

for 1 < p < N − $\ell$, and h₁ and h_N−${}_{\ell }$ are similar but with appropriately adjusted coefficients.

We simulate the evolution according to the same pulse shape as that applied in the experiment, with a time step of Δt = 0.15 ns and a bond dimension of 128. A comparison between the numerically simulated dynamics and the experimental results for different interaction strengths is shown in Fig. 4. As described in section ‘Extraction and scaling of correlation length’, deviations of the individual correlation functions from an exponentially decaying period-N density wave lead to systematic effects that dominate the uncertainty in the determination of the values presented in Fig. 4b. The comparison between experimental and numerical results is susceptible to multiple effects, including finite-size effects⁴⁷, accuracy of the approximate numerical methods used, experimental imperfections and data fitting, which contribute to the observed discrepancy.

Chiral clock models

QPTs in the Rydberg Hamiltonian (equation (1)) involving breaking of the ${{\mathbb{Z}}}_{n}$ (n ≥ 3) translational symmetry along one spatial direction are expected to be in the universality class of the extensively studied ${{\mathbb{Z}}}_{n}$ CCMs^{10,11,28,48,49,50,51}. To elucidate this connection, let us focus on n = 3 and consider the case when V₁ ≫ |Ω|, |Δ|; that is, nearest-neighbour interactions are strong enough to effectively preclude two neighbouring atoms from simultaneously being in the Rydberg state. Because van der Waals interactions decay rapidly as V_x = C₆/x⁶, we neglect couplings beyond the third-nearest neighbour by approximating V_x ≈ 0 for x ≥ 3, leading to a truncated model of the form:

$${H}_{{\rm{Ryd}}}=\sum _{i=1}^{N}\frac{\Omega }{2}\left(\left|{g}_{i}\right\rangle \left\langle {r}_{i}\right|+\left|{r}_{i}\right\rangle \left\langle {g}_{i}\right|\right)-\Delta {n}_{i}+{V}_{2}{n}_{i}{n}_{i+2}$$

(12)

supplemented with the constraint n_in_i+1 = 0.

The Hamiltonian in equation (12) can be mapped to a system of hard-core bosons, in which no more than one boson can occupy a single site. This follows upon identifying the state in which the atom at site i is in the internal state $\left|r\right\rangle$ $\left(\left|g\right\rangle \right)$ with the presence (absence) of a boson. By defining the bosonic annihilation and number operators, b_i and ${n}_{i}={b}_{i}^{\dagger }{b}_{i}$, respectively, we obtain

$${H}_{{\rm{b}}}=\sum _{i=1}^{N}\frac{\Omega }{2}({b}_{i}^{\dagger }+{b}_{i})-\Delta {n}_{i}+{V}_{2}{n}_{i}{n}_{i+2}$$

(13)

together with n_in_i+1 = 0. This model (often referred to as the U–V model) was shown by refs ^24,52 to exhibit a phase transition in the universality class of the three-state CCM, over a set of parameters.

The ${{\mathbb{Z}}}_{n}$ CCM is a simple extension of the transverse-field Ising model, in which each spin is promoted to have n > 2 states. However, instead of extending the symmetry from ${{\mathbb{Z}}}_{2}$ to ${{\mathbb{S}}}_{n}$, which would result in the n-state Potts model⁵³, the interactions are constructed to be invariant under ${{\mathbb{Z}}}_{n}$ transformations. With n = 3, the three-state CCM is defined by the Hamiltonian^49,51

$${H}_{{\rm{CCM}}}=-f\sum _{j=1}^{N}{\tau }_{j}^{\dagger }{{\rm{e}}}^{-i\varphi }-J\sum _{j=1}^{N-1}{\sigma }_{j}^{\dagger }{\sigma }_{j+1}{{\rm{e}}}^{-i\theta }+{\rm{h}}{\rm{.c}}{\rm{.}}$$

(14)

acting on a one-dimensional chain of N spins. The three-state spin operators τ_i and σ_i, which can be represented as

$$\tau =\left(\begin{array}{ccc}1 & 0 & 0\\ 0 & \omega & 0\\ 0 & 0 & {\omega }^{2}\end{array}\right),\,\sigma =\left(\begin{array}{ccc}0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0\end{array}\right)$$

(15)

act locally on site i, and each satisfy

$${\tau }^{3}={\sigma }^{3}={\rm{1,}}\hspace{2.77626pt}\sigma \hspace{2.77626pt}\tau =\omega \tau \hspace{2.77626pt}\sigma ;\hspace{2.77626pt}\omega \equiv exp\left(2{\rm{\pi }}i/3\right)$$

(16)

Here, ϕ and θ define two chiral interaction phases: to describe spatially ordered phases, we need ϕ = 0, where time reversal and spatial parity are both symmetries of the Hamiltonian but a purely spatial chirality is still present. We note that H_Ryd does not break time-reversal symmetry, necessitating the choice of ϕ = 0 in the quantum clock model (equation (14)). However, with both ϕ and θ non-zero, time-reversal and spatial-parity (inversion) symmetries are individually broken but their product is preserved.

As depicted in Fig. 4a, a generic state in the Hilbert space of the ${{\mathbb{Z}}}_{3}$ CCM can be mapped to one of three states of a clock according to the eigenvalue 1,ω or ω² of the operator σ at each site. Consequently, there can be two domain walls in the system that differ in their energies, depending on whether the clock rotates clockwise or anticlockwise upon crossing the wall. With ϕ = 0 and θ ≠ 0, these have different energies, 2Jsin[(π/6)–θ] and 2Jsin[(π/6)+θ], and are thus inequivalent, leading to a chirality in the system, which is absent for ϕ = θ = 0.

On setting both ϕ = θ = 0, H_ccm reduces to the Hamiltonian for the three-state Potts model, which possesses a larger symmetry, ${{\mathbb{S}}}_{3}$; the concomitant order–disorder phase transition has critical exponents z = 1, ν = 5/6^53,54,55 and, accordingly, μ ≈ 0.45. We note that these exponents are fundamentally distinct from those of the ${{\mathbb{Z}}}_{3}$ CCM; namely, z ≈ 1.33 and ν ≈ 0.71, yielding μ_CCM ≈ 0.37. The Rydberg Hamiltonian described in the main text contains a point along the phase boundary for which the condition of ϕ = θ = 0 is fulfilled, and with fine-tuned pulses it may be possible to explore the critical properties of the three-state Potts model.

For n = 4, the transitions of both the Potts and the achiral clock model are in the Ashkin–Teller universality class^56,57. The critical exponents of the four-state Potts model are z = 1 and ν = 2/3 (implying μ = 0.40), whereas the four-state achiral clock model is equivalent to two uncoupled Ising systems with z = 1 and ν = 1. With a non-zero chirality, however, it is believed that there is no direct transition from the ordered to the disordered phase in the four-state CCM, because an intermediate gapless incommensurate phase always intervenes^11,28,58.