Main

In parallel to investigations into electronic topological insulators, the recent demonstration of photonic topological insulators5,6,7 has shown that topological phenomena are not limited to the motion of electrons in solid-state materials. In fact, topological protection is a general wave phenomenon that applies equally well to many wave systems, including electromagnetic waves5,6,7,8,9,10,11,12,13,14,15, acoustic waves16,17, mechanical waves18,19 and cold atoms20,21. Among these, photonic topological systems have been found to be useful in demonstrating effects that would otherwise be unreachable in the context of condensed-matter physics, such as Anderson localization22,23, very strong strain24, non-Hermitian behaviour25 and the concept of topological bound states in the continuum26. Furthermore, topological photonic systems provide a complementary set of potential technological applications, including new mechanisms for integrated optical isolation and general robustness to imperfections in the fabrication of photonic devices.

Here we demonstrate a topological Anderson insulator. Our experiments are carried out in a photonic platform, as proposed theoretically27, based on a two-dimensional time-reversal-symmetry-broken Floquet topological insulator. In particular, when sufficient disorder is introduced, we enter the topological phase and observe unidirectional edge transport. Our key result, which demonstrates the possibility of inducing a topological phase using disorder, is universal and carries over to different dimensions28 and to symmetry-protected topological phases4,35. The experimental platform that we use is an array of evanescently coupled helical waveguides29, where the diffraction of light through the system is described by the paraxial wave equation, which is mathematically equivalent to the Schrödinger equation. A closely related system has been used for the observation of Floquet photonic topological insulators5.

To explain the mechanism that underlies our photonic topological Anderson insulator, we start with a honeycomb lattice of helical waveguides5, which is a photonic Floquet topological insulator. The equation that describes the diffraction of a paraxial beam of light in this lattice can be written, under the tight-binding approximation, as

$$i{{\rm{\partial }}}_{z}{\psi }_{i}=c\hspace{-2.77626pt}\sum _{j({\rm{n}}{\rm{n}}\hspace{1pt}i)}{{\rm{e}}}^{-i{\boldsymbol{A}}(z)\cdot {{\boldsymbol{r}}}_{i,j}}{\psi }_{j}+{m}_{\delta }{\delta }_{i}{\psi }_{i}\equiv \sum _{j}{\hat{H}}_{ij}(z){\psi }_{j}$$
(1)

where z is the distance of propagation along the waveguide axis, ψi is the envelope function of the electric field in the ith waveguide, c is the coupling strength between waveguides, A(z) = kRΩa(cos(Ωz), sin(Ωz), 0) is the gauge field induced by the helicity, k is the wavenumber of the light in the medium (fused silica), R is the radius of the helix, Ω is the longitudinal frequency associated with the helix, a is the nearest-neighbour spacing and ri,j is the displacement vector pointing from waveguide i to waveguide j. The honeycomb lattice comprises two triangular sublattices. The parameter δi takes the value 1 in one sublattice and −1 in the other, such that the on-site energies of the two are separated by the detuning 2mδ. Equation (1) defines \(\hat{H}(z)\) as the Hamiltonian at propagation distance z, and the summation therein is taken over nearest-neighbour waveguides. This is exactly the Schrödinger equation, where z takes the role of time. Because A(z) is z-dependent and periodic, solutions to equation (1) can be obtained by using Floquet’s theorem. Thus, the band structure can be obtained by diagonalizing the unitary evolution operator for one period30. Detuning the two triangular sublattices breaks the inversion symmetry of the structure and opens a trivial bandgap. This can be quantified with a mass mδ associated with the effective Dirac equation of the honeycomb lattice in the absence of the periodic driving. In the undetuned case (mδ = 0), the Dirac-cone dispersion is equivalent to that of massless relativistic particles. Such detuning can be realized experimentally in waveguide arrays by allowing the two honeycomb sublattices to have different refractive indices.

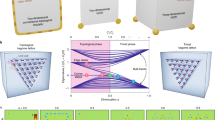
The mechanism according to which we realize the photonic topological Anderson insulator is depicted schematically in Fig. 1a. The band structure of the honeycomb lattice with straight and identical waveguides, so that the induced gauge field A(z) = 0 and mδ = 0, is shown in Fig. 1b. This band structure corresponds to that of a ribbon (associated with the zigzag edge of graphene31). As known in graphene physics, the ribbon band structure exhibits two Dirac cones (red ellipses in Fig. 1b) that are connected by a flat band of edge states31. When the waveguides follow a helical trajectory such that A(z) is non-zero (Fig. 1c), the z-reversal symmetry is broken and a bandgap opens. In this case, each valley acquires an opposite mass: mτ and −mτ for the left and right valleys, respectively. These opposite masses imply that the edge states cross the bandgap, with each edge state localized to opposite sides of the ribbon. Therefore, the bandgap is topological; the edge states form a single backscattering-free chiral edge state that is localized to the edge of the structure. This is the essence of a Floquet topological insulator in the honeycomb system5.

Fig. 1: Floquet topological Anderson insulator in a detuned honeycomb lattice.
figure 1

a, Mechanism for realizing the topological insulator phase in a photonic waveguide lattice. The white arrows indicate the trajectory through the phase diagram in the experimental protocol. The parameters for the band-structure calculations are chosen for illustration purposes. b, Band structure for a trivial honeycomb lattice with straight waveguides. The red ellipses indicate the Dirac cones. c, Time-reversal symmetry is broken by helical waveguide trajectories, opening a topological bandgap. d, Breaking the parity symmetry of the structure by detuning the sublattices sufficiently causes a trivial bandgap to form. e, Sufficiently strong disorder suppresses the effect of the parity-symmetry-breaking terms and moves the system into the topological Anderson insulator phase. The band structure shown in this case is for illustration purposes; there is no well defined band structure in the disordered case.

Full size image

Consider now what happens when the sublattices of the Floquet topological insulator are detuned so that the two sublattices exhibit different refractive indices. Introducing non-zero detuning breaks the inversion symmetry of the lattice, which adds a positive mass term mδ to each valley. If the detuning is large enough (mδ > mτ), then the masses mτ + mδ and −mτ + mδ in both valleys become positive and the bandgap becomes trivial (Fig. 1d). In other words, the outcome of a sufficiently detuned honeycomb lattice of helical waveguides is a topologically trivial system with broken inversion and time-reversal symmetry. This is where disorder comes into play: as was recently proposed27, this system can be brought into a topologically non-trivial phase using disorder. More specifically, it has been shown27 (using the Born approximation) that introducing on-site disorder, which is achieved by randomizing the refractive-index contrasts of the waveguides, causes an effective decrease in the detuning mδ. The decrease in mδ grows stronger as the strength of the disorder is increased. Therefore, upon introducing disorder and increasing its strength, the mobility gap closes when mτ = mδ and reopens for mτ > mδ. When the gap reopens, the system is topological (Fig. 1e). This is precisely the effect of photonic topological Anderson insulators: adding disorder brings the system from being topologically trivial (mδ > mτ) to topologically non-trivial (mτ > mδ).

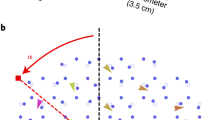
A schematic depiction of the waveguide configuration is shown in Fig. 2a. In this setting, it is essential to control which states are excited. We do that by adding a one-dimensional auxiliary array—a ‘straw’—through which we selectively excite the modes of the system at a fixed energy (kz). More specifically, in a one-dimensional waveguide array, tilting the phase front of the wave that illuminates the input facet determines the momentum of the excited Bloch mode. Here, such selective excitation is especially important because we would like to excite states entirely within the gap, to determine whether the gap exists and whether it is trivial or topological. By controlling the tilt angle of input of the beam, we can control kx, the Bloch wavevector in the horizontal direction. The band structure (kz versus kx) of the straw is shown in the inset in Fig. 2a. We fix kz (the Floquet quasienergy) by choosing kx, and kz is conserved as the beam travels through the straw and enters the honeycomb array. Thus, simply by changing the incidence angle of the beam, we can tune the quasienergy of the modes that are excited in the structure. The bandwidth in kz of the straw depends on kx and is relatively wide (determined by the number of sites in the straw and input beam), limiting our ability to perform precise spectroscopy. However, it remains a highly useful tool for selective excitation of wave packets in the honeycomb lattice.

Fig. 2: Set-up and functionality of the lattice system.
figure 2

a, Hybrid structure composed of a one-dimensional straw and a two-dimensional honeycomb lattice of helical waveguides (top), along with the corresponding dispersion relations (bottom). b, Determining the correct input angle for the incident light, such that a chiral edge state in the topological gap is excited. Two experimental images are shown, for kx = π/(2a) and kx = 3π/(4a); the excitation in the dispersion relation is sketched in the bottom plots of a. If the launch angle does not correspond to excitation in the gap, extensive coupling into the lattice bulk is observed. a.u., arbitrary units. c, Changing the input position (indicated by the white arrows) facilitates the observation of the evolution of the edge states as they propagate along the edge and pass the upper corner, never penetrating into the bulk.

Full size image

We first consider a system that breaks z-reversal symmetry (mτ ≠ 0) with identical (non-detuned) waveguides (mδ = 0), and repeat the previous realization of a Floquet topological insulator5 (see Methods for details). Owing to the helicity of the waveguides, the system has a topological bandgap at quasienergy kz = 0, and we expect to find a chiral edge state in this bandgap (the Floquet band structure is shown in the inset to Fig. 2a). This is precisely what we see. In Fig. 2b we show the output facet of the array in the case where kz lies in the bandgap (top) and the case where it lies in the band (bottom). When kz is in the gap, a chiral edge state is excited: the optical wave packet is launched from the straw and couples to the chiral edge state, where it propagates unidirectionally upwards in a clockwise direction around the honeycomb lattice, but does not penetrate into the lattice. On the other hand, when kz lies in the band, the wave packet couples to bulk states; hence, it penetrates into the lattice and spreads into the array, so does not stay confined to the edge. The evolution of the edge state is shown in Fig. 2c. As the input beam is brought closer to the array, the edge state travels farther along the edge until it passes the top corner. The fact that it moves only upwards, and stays confined to the edge, is a signature of the chirality of the edge state. We note that for the choice of parameters of the waveguide array used in the experiment the longitudinal frequency of the helix Ω is smaller than the total bandwidth (6c) in the absence of the helix. This results in an additional topological gap, which opens at a quasienergy of around kz = Ω/2 and hosts chiral edge states, as shown in Fig. 2a. However, by using the selective excitation through the straw, in this experiment we always excite states with quasienergies close to kz = 0 and do not probe states with quasienergy near kz = Ω/2.

We now describe the probing of a series of helical photonic lattices, where we introduce detuning between the sublattices (mδ ≠ 0) of the honeycomb structure by making their refractive indices different. In practice, this is done by changing the speed of the laser-writing beam during the fabrication process (a higher writing speed results in a lower refractive index of the waveguides). In a series of six waveguide arrays, we systematically increase this detuning, decreasing the gap size as mδ increases, and examine how much the wavefunction launched through the straw penetrates into the lattice (plotted in Fig. 3). To do that, we choose kx = π/(2a), where the Bloch wavenumber in the straw corresponds to the value of kz in the centre of the bandgap of the honeycomb lattice. For sufficiently strong detuning mδ, we observe a sharp decrease in the penetration of light along the edge, which corresponds to the closing of the topological bandgap and the reopening of the trivial bandgap at kz = 0. This observation constrains mδ to be larger than 1.57 cm−1, although precise determination of the on-site waveguide propagation constants within the array is not possible (owing to the exponential sensitivity of the refractive index to write speed and the effect of the lattice environment on the individual waveguides). Indeed, in the trivial gap, no states are present, and there is a dramatic drop in the penetration into the array along the edge. The inability to couple to edge states establishes that we have introduced sufficiently strong detuning, mδ, to have opened the trivial bandgap, which does not support edge modes.

Fig. 3: Engineering the topologically trivial phase.
figure 3

For sufficiently strong detuning between the sublattices of the honeycomb lattice, a trivial gap opens, such that the chiral edge state ceases to exist and all incident light is reflected back into the straw. The experiments show the light-intensity pattern as it exits the helical waveguide array (insets; colour scale as in Fig. 2) and the measured integrated intensity at the boundary as a function of detuning (main panel; in units of translation velocity of the writing laser). For zero detuning, the incident light resides only on the edge (indicating the topological insulator phase). When the detuning is small, the system is still in the topological phase and almost all the incident light resides on the edge. When the detuning is increased further, the system becomes topologically trivial and the incident light does not penetrate along the edge. There is no disorder in this lattice. The error bars indicate measurement uncertainty, and the confidence interval is about 0.06 of the maximum intensity observed (normalized to unity).

Full size image

Next, we introduce on-site disorder and demonstrate the formation of the photonic topological Anderson insulator by observing whether the mid-gap excitation gives rise to coupling to a topological edge state. The disorder enters equation (1) on the right-hand side via an additional term, wriψi, where ri is a uniformly distributed random variable between −0.5 and 0.5 and w is the strength of the disorder. We find that for sufficiently strong disorder (corresponding to a maximum variation in laser write speed of 8 mm min−1), the mid-gap excitation is able to couple into the lattice, staying largely confined to the edge (see Fig. 4a–c). As we move the input beam closer to the array, the light coupled into the array propagates farther along the edge, much as in the non-disordered topological system (with mδ = 0) of Fig. 2c. The beam moves up along the left edge, implying the presence of a chiral edge state (that was not present when the system was not disordered). We find the group velocity of the edge state to be 21 μm cm−1. We fit the profile of the excited wavefunction and find that it decays exponentially away from the edge, consistent with having excited predominantly the edge states (see Methods). For comparison, we show the same scenario but with no disorder and with the same mδ in Fig. 4d–f. When no disorder is present, there is no observable edge excitation and minimal bulk penetration; that is, the beam launched into the topologically trivial photonic bandgap is reflected. The small amount of bulk penetration seen in Fig. 4d–f probably arises from the finite bandwidth of the input beam in kz. The appearance of the chiral edge state when the disorder is sufficiently strong is evidence of the photonic topological Anderson insulator phase27. In Fig. 4g we show a phase diagram that indicates the topological invariant that counts the number of edge states at quasienergy kz = 0 as a function of detuning mδ and disorder strength w (a full description of the topological invariant32,33 that we use is provided in Methods). The phase diagram shows that adding sufficiently strong disorder to the detuned lattice in the trivial phase necessarily takes the system into the topological phase. For considerably stronger disorder, localization sets in, making the system Anderson-localized4.

Fig. 4: Formation of the photonic topological Anderson insulator.
figure 4

a–c, When sufficient disorder is added, the system is driven into the topological Anderson insulator phase and chiral edge states form. This is demonstrated by moving the excitation in the straw (solid arrows) close to the (disordered) honeycomb lattice, so that the edge state crawls up the edge (dashed arrows). The excitation in the straw is far from the honeycomb lattice (22 waveguides away; a); the excitation is at an intermediate distance from the lattice (11 waveguides away; b); and the excitation is close to the lattice (4 waveguides away; c). The dashed boxes indicate the honeycomb waveguide array. d–f, By contrast, in the fully ordered, detuned helical honeycomb lattice, essentially all light is reflected into the straw, with only a small part penetrating into the bulk without exciting any edge mode. The excitation in the straw is far from the honeycomb lattice (d); the excitation is at an intermediate distance from the lattice (e); and the excitation is close to the lattice (f) (distances as in a– c). g, Phase diagram showing the trivial and topological phases as a function of the detuning mass, mδ, and disorder strength, w, obtained using experimental parameters (see Methods). The red arrow indicates the trajectory through the phase diagram as the system starts from the trivial phase and enters the topological phase with increasing disorder strength.

Full size image

The experiments presented here demonstrate the observation of a topological Anderson insulator using a photonic platform. Specifically, we have shown that a topologically trivial system can undergo a transition and become topological when disorder is added. This was carried out by observing the emergence of a chiral edge state upon introducing sufficiently strong disorder (where there was none with no disorder). The topological Anderson insulator phase is a clear example of the complex relationship between topology and disorder: it goes beyond the usual notion whereby sufficiently strong disorder destroys topologically protected transport1. It shows that disorder is a key variable in probing topological phases, in the sense that even in trivial systems topological behaviour can emerge when disorder is introduced at sufficient strengths. We expect that our experimental realization of this phase will stimulate a range of theoretical and experimental studies to explore the role of disorder in topological systems. This prompts various important questions, such as what happens to the topological Anderson insulator phase in the presence of interactions in optical, atomic and condensed-matter systems, and whether there is a topological Anderson insulator phase in the quantum many-body regime. The answers to these questions are now being brought within experimental reach.

After this paper was submitted, a related paper34 appeared on arXiv that reported the observation of a topological Anderson insulator in one-dimensional atomic wires.

Methods

Details of the fabricated lattice

In our waveguide structures, we use a helix pitch of Z = 1 cm, a radius of R = 10 μm and a nearest-neighbour spacing of a = 14 μm; at our probe wavelength (λ = 633 nm), this corresponds to a dimensionless gauge field strength of |A| = kRΩa = 1.26, with k = 2πn0/λ, Ω = 2π/Z, an ambient refractive index n0 = 1.45 and a = 14 μm nearest-neighbour spacing, which gives rise to a nearest-neighbour coupling strength of 1.8 cm−1. The waveguides are written at an average writing speed of 90 mm min−1. A broad input probe beam is incident on the straw, with a beam waist of approximately 100 μm.

Discussion of the topological invariant that characterizes the photonic topological Anderson insulator phase

The topological invariant that characterizes the non-interacting two-dimensional periodically driven systems (in the absence of any additional symmetry besides particle number conservation) is the winding number \({W}_{{k}_{z}}\), which depends on the quasienergy kz. For each quasienergy kz, the value \({W}_{{k}_{z}}\) is equal to the number of chiral edge states at that quasienergy32, 33. To compute the winding number for kz = 0, we first compute the Bott index of the Floquet band27, which lies in the quasienergy interval 0 ≤ kz ≤ Ω/2. This Bott index essentially counts27 the number of chiral edge states that traverse the gap at kz = Ω/2 less the number of chiral edge states that traverse the gap at kz = 0. In addition, we verify that for the range of mδ shown in Fig. 4 (mδ > 1.4 cm−1), the gap at kz = Ω/2 hosts a single chiral edge state for the entire range of parameters with no disorder. Therefore, we conclude that, throughout the range of parameters shown in Fig. 4g, a Bott index of 0 corresponds to a topological gap at kz = 0 and a Bott index of 1 corresponds to a trivial gap at kz = 0.

Decay length of the edge state

We extract the decay length of the edge state from the experimental data. To achieve this, we analyse the intensity profile of the light propagating along the edge. To average over the disorder potential, we integrate the intensity per pixel along a direction parallel to the edge, and obtain the averaged intensity as a function of distance from the edge. The intensity profile (Extended Data Fig. 1a) decays with increasing distance from the edge, with peaks at the waveguide positions. We fit the envelope of the intensity profile to an exponential decay, which results in a decay length of the edge state of 47 μm (Extended Data Fig. 1b). This length scale is much smaller than the system size (158 μm). This result demonstrates that the system is sufficiently large for us to have observed the edge state. We do not observe any light at the far edge of the sample (the edge opposite the point at which the straw meets the sample), which indicates that the system size is sufficiently large that there is no considerable coupling between edge states on opposite sides.

We compare the experimentally obtained value of the decay length of the edge states with theoretical values obtained from a numerical simulation of a tight-binding model. The simulations are run for lattices with 60 × 30 unit cells with periodic boundary conditions along y and open boundary conditions along x for a total time of N = 30 periods of rotation of the helices. The parameters for the tight-binding model are chosen as c = 1.8 cm−1, cnnn = 0.234 cm−1, mδ = 1.6 cm−1, Ω = 2π cm−1, kRΩa = 1.26 and w = 1.6 cm−1, where cnnn is the next-nearest-neighbour hopping strength. To extract the decay length from the numerical simulation, we numerically compute the Green’s function GN(r0, r, NT) = 〈r|U(t = NT, 0)|r0〉, where U(t = NT, 0) is the evolution operator over N periods. From the Fourier transform of the Green’s function in time, we compute gN(r0, r, ε) = 〈|GN(r0, r, ε)|2〉, where the angle brackets denote averaging over multiple realizations of the disorder. (For more details on the definition of these quantities, see ref. 27; in short, U(t, t0) is the time-dependent propagator from time t0 to t, |r0〉 and |r〉 are position eigenstates and ε is the quasienergy, equivalent to kz in the experiment.) For initial positions r0 localized on the edge and ε in the mobility gap (near quasienergy ε = 0), the function gN(r0, r, ε) shows propagation along the edge and an exponentially localized profile confined to the edge. We integrate gN(r0, r, ε = 0), averaged over 100 realizations, along the direction parallel to the edge (that is, we integrate over the y component of r). We extract the decay length from the decay profile of the result (which is a function of only the distance from the edge). The results (Extended Data Fig. 1c) give a decay length of 7a.

From our numerical simulations, we can also extract the group velocity along the edge. This is achieved by examining the dependence of gN, averaged along the x direction (perpendicular to the edge), as a function of time. The spread of this function along the y direction (parallel to the edge) can be quantified using a typical length scale36 \({\Lambda }_{y}^{{\rm{typ}}}(N)\), which is obtained by examining the inverse participation ratio of the disorder-averaged Green’s function (integrated over the x direction)3. In the inset of Extended Data Fig. 1c, we show the dependence of \({\Lambda }_{y}^{{\rm{typ}}}(N)\) on N, which clearly shows a linear growth indicating the ballistic nature of the edge state. The slope gives the velocity, which is 1.2a cm−1.

From the numerically obtained disorder-averaged Green’s function, we also extract the localization length of the bulk states. We take an initial position r0 in the bulk of the system and plot the corresponding function gN(r0, r, ε) = 〈|GN(r0, r, ε)|2〉 (Extended Data Fig. 1d). This yields a bulk localization length of 4a. Our numerical analysis thus shows that quasienergies near ε = 0 are indeed in a mobility gap. Furthermore, the bulk localization length in the mobility gap near ε = 0 is indeed sufficiently smaller than the system size.

Data availability

All data generated or analysed during this study are available from the corresponding author upon reasonable request.