Main

Quantum algorithms are predicted to provide a computational speed-up over their classical counterparts. To be implemented, these algorithms need to be compiled on specific quantum hardware to decompose global operations into the naturally available elementary gates. Given the stringent resource constraints offered by the noisy intermediate-scale quantum (NISQ) technology foreseeable in the next 5–10 years1, it is essential to optimize the use of every qubit and every gate cycle to enable successful near-term applications2. One effective strategy is to fully explore the hardware capabilities and diversify the available gate alphabets to optimize compilation3,4,5.

Several global or multi-qubit operations are textbook circuit components essential for building quantum algorithms6. The best-known examples are the quantum arithmetic circuits used in Shor’s factoring algorithm7 and the multiply controlled gates used in Grover’s search algorithm8. The latter are nontrivial multi-qubit quantum logics that perform unitary operations on target qubits conditioned on the states of all the control qubits. Relevant applications include quantum error correction9,10,11, quantum simulation12 and quantum machine learning13. One brute-force approach for an extensible implementation of these large operations is to decompose them into a finite set of universal gates. For example, the generalized Toffoli gate, that is, the n-qubit controlled-NOT (CNOT) gate, can be constructed using quadratically many (\({{{\mathcal{O}}}}({n}^{2})\)) two-qubit CNOT gates plus single-qubit gates on a qubit array with all-to-all connections14 and even more gates on devices with nearest-neighbour couplings15. A more efficient approach is to concatenate together small Toffoli gates, assisted by ancilla qubits6,16. Leaving aside the extra resources needed, it is challenging to achieve high-quality small Toffoli gates. Apart from brute-force decomposition, small Toffoli gates may be obtained via one-step manipulations17,18,19,20,21,22,23 or by leveraging either, again, ancilla qubits24,25 or ancilla levels26,27,28,29,30. Despite successful demonstrations of single small Toffoli gates in various systems, a scalable synthesis has never been experimentally realized because of the prohibitive implementation cost. A scheme that is, at the same time, hardware-efficient, low-depth, easy to control and compatible with state-of-the-art hardware31,32,33 is yet to be realized. We note that native global entangling operations are available in ion traps, which have unique all-to-all connections34, and in specially designed superconducting circuits35. However, these global operations are based on pairwise interactions and thus not equivalent to the multiply controlled gate, although they may be used for faster synthesis36.

In this Article we introduce a quantum version of the AND (QuAND) gate, a novel gate type that, as inspired by ref. 28, utilizes an ancilla level for temporary information storage only. The QuAND gate enables a scaling advantage in the circuit depth when synthesizing arithmetic circuits and multiply controlled gates. We experimentally implement QuAND gates on a superconducting quantum processor featuring simplified wiring and low crosstalk, and demonstrate a linear-depth synthesis of generalized Toffoli gates with up to eight qubits, that is, a total of seven control qubits. Our demonstration is large in size and shows high performance (truth table fidelity: 89.1%, 53.2% and 39.1% for n = 4, 6 and 8, respectively). Using these gates, we perform Grover’s search algorithm with multiple amplification cycles and achieve significant success probabilities (46.8% and 3.9% for searches of 16 and 64, respectively), demonstrating the feasibility of our method for scaled applications. Note that alternative efficient compilation schemes have been proposed in recent theoretical studies11,37. However, these schemes generally require the manipulation of a multi-level system with high degrees of freedom, adding considerable operational complexity.

Simplifying quantum logic using QuAND gates

The logic AND operation is a basic ingredient for designing both classical and quantum algorithms. Unfortunately, it cannot be directly implemented on qubits because of the reversibility of quantum operations. One workaround is to extract it from a Toffoli gate at the cost of an extra qubit6. This overhead hinders scaled implementation on realistic hardware. In this Article we propose a resource-efficient QuAND gate scheme (Fig. 1a) in which one of the two outputs registers the AND result of the inputs, that is, \({\left|{{{\rm{A\& B}}}}\right\rangle}\), and the other output \({\left|{{{\rm{C}}}}\right\rangle}\) spans three different states, in our case, \({\left|{1}\right\rangle}\), \({\left|{2}\right\rangle}\) and \({\left|{0}\right\rangle}\) for input states \({\left|{00}\right\rangle}\), \({\left|{01}\right\rangle}\) and \({\left|{10}\right\rangle}\), respectively. The use of the ancilla level \({\left|{2}\right\rangle}\) preserves reversibility; the reverse QuAND gate simply switches the inputs and outputs. We refer to the AND-value qubit as the ‘parent’ and the other qubit as the ‘child’. The circuit notation, truth table and decomposition schemes of the QuAND gate and its reversal are illustrated in Fig. 1a. Here we decompose the QuAND gate (or its reversal) into a single-qubit X gate in front of (or after) an iSWAP-like operation between \({\left|{11}\right\rangle}\) and \({\left|{20}\right\rangle}\) (denoted iSWAP11−20), which is naturally available on our hardware, as shown later.

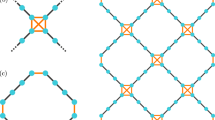
Fig. 1: Simplifying compilation using the quantum version of the AND (QuAND) gate.
figure 1

a, Circuit notation, truth table and decomposition of the QuAND gate and its reversal. The AND-value qubit, indicated by an &, is referred to as the ‘parent’, and the other qubit is referred to as the ‘child’. A QuAND gate is indicated by an arrow pointing from the child to the parent, with an arrow in the opposite direction indicating a reverse QuAND gate. Both can be synthesized with a single-qubit X gate and an iSWAP-like operation between \({\left|{11}\right\rangle}\) and \({\left|{20}\right\rangle}\), which is indicated by a double-cross sign with a dashed cross on the child qubit. b, Circuit decomposition of an n-qubit controlled-Z (CZ) gate on a 1D qubit chain using a sequence of QuAND gates, a CZ gate and a sequence of reverse QuAND gates, shown here with time progressing from left to right. During embedding, the sequentially applied QuAND gates register the AND results of all the qubits from the upper and lower halves of the chain onto the two root parents, Qk and Qk + 1, respectively. The embedded information is later released via the reverse QuAND gates to recover the original binary encoding. The CZ gate is only effective when all qubits are in state \({\left|{1}\right\rangle}\). c, Sketch showing a quantum processor with qubits connected in an arbitrary topology. A branching tree is enacted for implementing the QuAND gate sequence (arrows) with time progressing from dark blue to light green. The CZ gate is performed between the two root parents. The QuAND gate could also be performed across multiple processors (arrows pointing from outside) to efficiently implement global operations on a larger quantum network.

Full size image

One direct application of a QuAND gate is to simplify the compilation of large gate operations, in particular, multiply controlled gates, which are experimentally challenging to realize and the focus of this study. Figure 1b shows the circuit decomposition for an n-qubit CZ gate on a one-dimensional (1D) qubit chain divided into three stages: embedding, the controlled-unitary operation and recovery. Let \({\left|{s}\right\rangle }={\left|{s}_{1}{s}_{2}...{s}_{n}\right\rangle}\) (si = 0, 1) denote a basis state at the input. During embedding, we apply QuAND gates sequentially to the chain from both ends inward. At the end of the QuAND sequence, the two root parents in the middle, Qk and Qk + 1, temporarily register the AND result of all the qubits from the upper and lower halves of the chain, respectively. In other words, \({\left|{s}_{k}^{\prime}\right\rangle }={\left|{\wedge }_{i = 1}^{k}{s}_{i}\right\rangle}\) and \({\left|{s}_{k+1}^{\prime}\right\rangle }={\left|{\wedge }_{i = k+1}^{n}{s}_{i}\right\rangle}\), where ∧ is the notation for the global AND operation. Therefore, the subsequent CZ gate, which flips the wavefunction sign when \({\left|{s}_{k}^{\prime}{s}_{k+1}^{\prime}\right\rangle }={\left|11\right\rangle}\), is effectively a phase flip conditioned on all qubits, \({(-1)}^{{\wedge }{s}_{i}}\). The recovery sequence then transfers the state back to the original binary encoding and completes an n-qubit CZ gate. There are a total of 2n − 3 two-qubit gates in this sequence. The linear (\({{{\mathcal{O}}}}{(n)}\)) circuit depth (the number of two-qubit gate cycles) as a result of using QuAND gates manifests a scaling advantage over the quadratic depth when using only CNOT gates14. Note that the ancilla levels are used here only for the temporary storage of the state information and that only a state-transfer operation is needed, which is in contrast to schemes that require more complex, hard-to-engineer operations with ancilla levels29,30,37. Moreover, other types of multiply controlled gate, such as the generalized Fredkin (controlled-SWAP) gate, can be synthesized similarly. In fact, any classical circuit, such as Boolean logic and arithmetic circuits, can be constructed efficiently using QuAND and single-qubit gates, because the classical NAND gate is universal. Examples of quantum adder circuits are shown in SupplementarySection I.

An even more impressive scaling advantage can be achieved on qubit arrays with higher connectivity. To see this, it is helpful to first identify the key idea of our proposal, that is, to enact a branching tree graph on an arbitrarily connected qubit array and apply QuAND gates sequentially to register the AND results of neighbouring qubits onto the parents, layer by layer, from the leaves up to the root, as illustrated in Fig. 1c. Ignoring the constant, the optimal circuit depth is then equivalent to the depth of the tree. For example, the circuit depth can be reduced to \({{{\mathcal{O}}}}{(\sqrt{n})}\) on a 2D square array and to \({{{\mathcal{O}}}}({\log }_{2}{n})\) on a binary tree (SupplementarySection II); such polynomial or exponential speed-up in compiling global operations can constitute a huge boost for relevant quantum applications. In addition, because this scheme only requires that qubits be connected, it is well suited to a distributed quantum network where only sparse connections are likely to be available.

Implementing a QuAND gate with superconducting qubits

Our experimental device (Fig. 2a), tested inside a dilution refrigerator at a base temperature of 10 mK, consists of eight fixed-frequency transmon qubits38, known for long coherence and simplified control, arranged in a ladder array and interconnected via ten frequency-tunable couplers. The two couplers in the middle have no control lines, resulting in the qubit array having a ring topology. Each qubit has a dedicated readout resonator, and all the resonators share a common feed line enabling a multiplexed dispersive readout. The qubit frequencies are arranged alternately between a red band (6.2–6.5 GHz) and a blue band (7.0–7.3 GHz) along the ring; such frequency planning helps suppress microwave crosstalk. The qubits are strongly coupled (with an interaction strength of g/2π ≈ 100 MHz) to their adjacent couplers, which are tunable via their flux biases Φe. The couplers are designed to turn off the inter-qubit coupling via multi-path interference39 near their maximum frequencies (8.0–8.4 GHz) at Φe = 0, which resolves the frequency-crowding problem and reduces the nearest-neighbour ZZ crosstalk down to ~50 kHz. In addition, the use of tunable couplers enables fast two-qubit gates between the fixed-frequency qubits, for example, the adiabatic CZ gate40,41. We use a shared control line to deliver the diplexed signals for both the qubit (4–8 GHz) and coupler (DC-1 GHz) control; these signals are synthesized at room temperature and transmitted to the device inside the dilution refrigerator. This design substantially simplifies the wiring effort both on the chip and inside the refrigerator, promising higher scalability. See SupplementarySection III for details concerning the device and experimental set-up.

Fig. 2: Implementing the QuAND gate on a high-scalability superconducting quantum processor.
figure 2

a, False-colour micrograph of the device. Red and blue indicate the lower and higher fixed-frequency transmon qubits, respectively. b, Eigenenergies of states \({\left|{101}\right\rangle}\) and \({\left|{200}\right\rangle}\) (tri-mode notation) in a qubit–coupler–qubit subsystem versus the coupler-flux bias, Φe. The thin black line with the embedded arrowheads indicates the state trajectory for the iSWAP11−20 pulse sent to the coupler (inset), where Ap is the amplitude of the parametric drive on the flux pulse plateau. c, Measured final state probabilities in states \({\left|{11}\right\rangle}\) and \({\left|{20}\right\rangle}\) after the iSWAP11−20 pulse versus the parametric drive amplitude. The dashed line indicates a full iSWAP11−20 operation.

Source data

Full size image

The QuAND and iSWAP11−20 gates on our device were implemented using coupler-assisted level transitions. According to the tri-mode (\({\left|{{{\rm{qubit}}}},\,{{{\rm{coupler}}}},\,{{{\rm{qubit}}}}\right\rangle}\)) notation, the iSWAP11−20 gate is a full swap operation between \({\left|{101}\right\rangle}\) and \({\left|{200}\right\rangle}\), which is realized by a flux pulse sent to the coupler. To activate such a transition we applied a flux pulse to the coupler, where the pulse consisted of an adiabatic rise and fall (40 ns each) separated by a sinusoidal pulse (30 ns), as illustrated in Fig. 2b. Under this pulse, as shown by the thin black line with embedded arrowheads, the system state first follows an adiabatic excursion on state \({\left|{101}\right\rangle}\) from the idling bias Φe = 0 Φ0 to Φe = 0.26 Φ0, then transits to \({\left|{200}\right\rangle}\) via a parametric drive resonant with the instantaneous frequency gap between \({\left|{101}\right\rangle}\) and \({\left|{200}\right\rangle}\), and eventually adiabatically returns to the idling bias. There are two major concerns when choosing the transition bias. First, the flux-induced \({\left|{101}\right\rangle}\) ↔ \({\left|{200}\right\rangle}\) transition is inhibited at Φe = 0 but is significantly enhanced at a sufficiently large bias as a result of wavefunction hybridization, as is evident by the strong bending of the energy levels42. Second, a proper bias is critical to avoid spurious transitions (SupplementarySection IV).

In the experiment, we calibrated the iSWAP11−20 gate by optimizing both the frequency and the amplitude of the parametric pulse. An example of the continuous swapping between \({\left|{11}\right\rangle}\) and \({\left|{20}\right\rangle}\) as a function of the pulse amplitude Ap is shown in Fig. 2c. The average observed transition error of 2.7% is primarily caused by energy relaxation during the pulse. All data presented here were corrected to account for the state preparation and measurement error. Note that, so far, we have ignored the phase factor of the iSWAP11−20 gate. In fact, a pair of iSWAP11−20 gates exchange the excitation back and forth, leading to a conditional phase on state \({\left|{11}\right\rangle}\), which can be calibrated away by adjusting the relative phase between the two iSWAP11−20 gates. SupplementarySection V provides details concerning the gate scheme, calibration procedures and data processing.

Low-depth synthesis of multi-qubit Toffoli gates

Using calibrated QuAND gates, we demonstrate the low-depth synthesis of a generalized Toffoli gate, which is equivalent to the n-qubit CZ circuit described in Fig. 1b, with two additional single-qubit gates. Figure 3a illustrates how we compile, on the 8-qubit ring, an n-qubit CZ gate with incremental size (n = 4, 6 and 8) in linear time steps. We characterize these large gates by measuring their truth tables, Uexp, that is, the output state probability distribution for each of the 2n input states, which are shown in Fig. 3b. The truth-table fidelities, \({{{{\mathcal{F}}}}}_{{{{\rm{tt}}}}}={\frac{1}{{2}^{n}}}{{{\rm{Tr}}}}({U}_{\exp }{U}_{\rm{ideal}})\), are 89.1%, 53.2% and 39.1% for n = 4, 6 and 8, respectively. We note that the 4-qubit Toffoli truth-table fidelity is higher than the measured gate fidelity (83.6%) from process tomography (Supplementary Section VI), as a result of underestimated phase errors when measuring the truth table. The relaxation-limited gate fidelities (total duration) for the 4-qubit, 6-qubit and 8-qubit Toffoli gates are 92.5% (0.4 μs), 66.7% (1.3 μs, staggered pulses) and 62.3% (1.1 μs), respectively, and are responsible for ~70% of the total error; the remaining error is due in part to dephasing and in part to stray couplings42,43,44.

Fig. 3: Low-depth synthesis of generalized Toffoli gates.
figure 3

a, Schematic showing the compiled sequence for implementing the 4-qubit (left), 6-qubit (centre) and 8-qubit (right) CZ gate circuits described in Fig. 1b on the 8-qubit processor with qubits indexed from 0 to 7. The arrows denote the QuAND gate sequence, with time progressing from dark blue to light green. We have omitted the reverse QuAND sequence. b, Measured truth tables of the corresponding generalized Toffoli gate. In these examples, the controlled-NOT operation is performed on Q7 in all cases.

Source data

Full size image

Grover’s search algorithm

Finally, we performed Grover’s search algorithm as a complementary method to benchmark our multi-qubit gates. The core steps of this algorithm encode a solution bit-string j with a phase oracle \({O}_{j}={\sum }_{s\ne j}{\left|{s}\right\rangle }{\left\langle {s}\right|}-{\left|{j}\right\rangle }{\left\langle {j}\right|}\), a unitary that accesses the input function, and amplify the probability of finding \({\left|{j}\right\rangle}\) via phase diffusion, with each step containing an n-qubit CZ gate (Fig. 4a); these two steps may be repeated for further amplification. Here, the phase oracle performs a conditional phase flip on \({\left|{j}\right\rangle}\); therefore, an arbitrary oracle can be constructed from an n-qubit CZ gate with additional pairs of X gates applied to qubits being conditioned on \({\left|{0}\right\rangle}\) instead of \({\left|{1}\right\rangle}\). We note that there is an alternative way to implement Grover’s search by replacing the diffuse operator with single-qubit gates at the cost of more oracle queries45.

Fig. 4: Demonstration of Grover’s search algorithm with multiple amplification cycles.
figure 4

a, Circuit diagram implementing Grover’s search algorithm. In this example, the encoded solution is 110101. Y±1/2 indicates a ±π/2 rotation about the Y axis. b, Measured output state probability distribution for each of the 2n encoded states in the 4-qubit and 6-qubit Grover’s search algorithms. c, Average algorithm success probabilities (dots) and four times the standard deviations (error bars) of all 2n cases versus the number of oracle-amplification cycles. The solid lines are fits to equation (1) with finite gate fidelity. The dashed lines correspond to the ideal case with unity fidelity.

Source data

Full size image

Figure 4b shows the results of the 4-qubit and 6-qubit single-solution Grover’s search algorithms with one oracle-amplification cycle (the Supplementary Information provides extended data of the multi-solution Grover’s search). The diagonal matrix elements correspond to the probabilities of finding the correct states, that is, the algorithm success probability (ASP), and are substantially higher than the other elements, on average 34.2% versus 4.4% for the 4-qubit Grover’s search and 3.9% versus 1.5% for the 6-qubit Grover’s search, showing the effectiveness of the amplification. Because of its insufficient fidelity, the 8-qubit Grover result (not shown) does not display a significant ASP gain.

To optimize the ASP, we tested Grover’s search algorithm with multiple rounds of amplification. As shown in Fig. 4c, the average ASP in the 4-qubit case shows a clear improvement to 46.8% with one additional cycle (M = 2), and a clear dependence is visible up to ten cycles, that is, a total of 20 CCCZ gates, due to the high gate fidelity. Ignoring contributions from the single-qubit gate error, which is estimated to be 0.14% from simultaneous randomized benchmarking, we developed a simplified model for estimating ASP (SupplementarySection VII):

$${{{\rm{ASP}}}}={{{{\mathcal{F}}}}}^{2M}{\sin }^{2}{\left(({2M+1}){\arcsin }\left({2}^{-\frac{n}{2}}\right)\right)}+{\frac{1-{{{{\mathcal{F}}}}}^{2M}}{{2}^{n}}},$$
(1)

where \({{{\mathcal{F}}}}\) is the n-qubit CZ gate fidelity. Fitting the data to equation (1) gives \({{{\mathcal{F}}}}= 84.4\%\) and 50.9% for the 4-qubit and 6-qubit cases, respectively, which are close to the above-measured truth-table fidelities.

Discussion

The low-depth circuit synthesis using the QuAND logic enabled our implementation of multiply controlled gates and Grover’s search algorithm at a high scale, confirming the feasibility of a scalable and resource-efficient approach to simplify algorithm compilation. At the essence of our scheme is engineering a coherent, selective transition between one of the computational levels and an ancilla level, enabling the quantum analogue of AND logic. Therefore, the scheme can be applied to other quantum computing platforms by encoding the ancilla level using, for example, different internal states in ion traps46, path variation in optical systems26, valley freedom in Si/SiGe systems47 and nuclear spin in the Si:P system48. This study should not only stimulate interest in exploring alternative compilation schemes using QuAND logic, but should also help reduce hardware-related challenges, in particular, the connectivity problem for which solid-state devices have long been criticized. With further improvements to fidelity, our work will help close the gap between most anticipated near-term applications and available NISQ devices.

Methods

Coupler-assisted iSWAP11−20

In the tri-mode (Q–C–Q) system, the static part of the Hamiltonian in the laboratory frame is (ℏ = 1):

$$\begin{array}{l}{H}_{{{{\rm{static}}}}}=\mathop{\sum}\limits_{i=1,\,2,\,{{{\rm{c}}}}}({\omega }_{i}{a}_{i}^{{\dagger} }{a}_{i}+\frac{{\alpha }_{i}}{2}{a}_{i}^{{\dagger} }{a}_{i}^{{\dagger} }{a}_{i}{a}_{i})\\ \qquad \quad +\mathop{\sum}\limits_{i=1,\,2}{g}_{i{{{\rm{c}}}}}({a}_{i}^{{\dagger} }+{a}_{i})({a}_{{{{\rm{c}}}}}^{{\dagger} }+{a}_{{{{\rm{c}}}}})+{g}_{12}({a}_{1}^{{\dagger} }+{a}_{1})({a}_{2}^{{\dagger} }+{a}_{2}).\end{array}$$
(2)

Here ωi and αi denote the frequency and the anharmonicity of mode i, and \({a_{i}^{\dagger}}\) is the corresponding annihilation(creation) operator. The qubits Q1 and Q2 couple to the coupler with coupling strength g1c and g2c, respectively, and to each other with a coupling strength g12. The time-dependent drive Hdrive = Hadia(t) + Hdia(t) can be divided into an adiabatic part Hadia(t) and a diabatic part, that is, the parametric drive, \({H}_{{{{\rm{dia}}}}}{(t)}={\xi (t)}{a}_{{{{\rm{c}}}}}^{{\dagger }}{a}_{{{{\rm{c}}}}}={A(t)\cos }({\omega }_{{{{\rm{d}}}}}{t}+{\theta }){a}_{{{{\rm{c}}}}}^{{\dagger }}{a}_{{{{\rm{c}}}}}\). ωd and θ denote the frequency and the phase of the parametric pulse, respectively. Note that we have absorbed into the adiabatic part a drive-amplitude-dependent frequency shift, which arises from the nonlinear relation between the coupler frequency and the applied flux. Following the instantaneous eigenbasis defined by Hstatic + Hadia(t), we may rewrite the approximate Hamiltonian of the two-level (\({\left|{i}\right\rangle}\) and \({\left|{j}\right\rangle}\)) system:

$${H}_{{{{\rm{TLS}}}}}{(t)}={\frac{1}{2}\left[{{{\varDelta }}}_{ij}+{\xi (t)}{\delta }_{ij}\right]{\hat{\sigma }}_{{{{\rm{z}}}}}+{\xi (t)}({n}_{ij}{\hat{\sigma }}_{-}+{{{\rm{h.c.}}}})},$$
(3)

where \({\hat{\sigma }}_{{{{\rm{z}}}}}={\left|{i}\right\rangle }{\left\langle {i}\right|}-{\left|\,{j}\right\rangle }{\left\langle \,{j}\right|}\), \({\hat{\sigma }}_{-}={\left|{i}\right\rangle \left\langle \,{j}\right|}\), Δij is the instantaneous level spacing, \({n}_{ij}={\left\langle {i}\right|{a}_{{{{\rm{c}}}}}^{{\dagger} }{a}_{{{{\rm{c}}}}}\left|\,{j}\right\rangle}\) and δij = nii − njj.

Defining the unitary operator \({{\varLambda }}{(t)}={\rm{e}}^{{{{\rm{i}}}}{\hat{\sigma }}_{z}[{{{\varDelta }}}_{ij}{\ t}+{\zeta (t)}{\delta }_{ij} \ ]/2}\), where \({\zeta (t)}={\int\nolimits_{0}^{t}\xi (t^{\prime} ){{{\rm{d}}}}t^{\prime}}\) and assuming a constant drive amplitude A(t) = b, we can express the effective Hamiltonian in the rotating frame as

$${H}_{\rm{TLS}}^{\prime}{(t)}={\Lambda}{H}_{\rm{TLS}}{\Lambda}^{\dagger}+{i}{\partial }_{t}{\Lambda}{\Lambda }^{\dagger} =\frac{1}{2}({\tilde{\Omega}}\,{\hat{\sigma }}_{-}+{{{\rm{h.c.}}}}),$$
(4)

where \({\tilde{\Omega }}={b\left[{J}_{0}(\frac{b{\delta }_{ij}}{{\omega }_{\rm{d}}})+{J}_{2}(\frac{b{\delta }_{ij}}{{\omega }_{\rm{d}}})\right]{n}_{ij}{\rm{e}}^{\rm{i}[({\Delta}_{ij}-{\omega }_{\rm{d}})t-\theta ]}}\). In the above equation, we have omitted fast oscillating terms and high-order Bessel terms in the Jacobi–Anger expansion. Here, it can be seen that the effect of the parametric modulation is similar to a Rabi drive between the two selected levels in the instantaneous eigenframe.

Under the resonant condition Δij − ωd = 0, the corresponding unitary operator in this subspace is

$${U}_{{{{\rm{TLS}}}}}^{\prime}={\left(\begin{array}{ll}\cos ({{\varOmega }}{t/2})&-{{{\rm{i}}}}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}\theta }{\sin }({{\varOmega }}{t/2})\\ -{{{\rm{i}}}}{{{{\rm{e}}}}}^{{{{\rm{i}}}}\theta }{\sin }({{\varOmega }}{t/2})&{\cos }({{\varOmega }}{t/2})\end{array}\right)},$$
(5)

where \({\Omega}={| \tilde{\Omega}|}\) after ignoring an irrelevant initial phase from nij. The dynamics is a coherent Rabi cycling with an effective Rabi frequency Ω, in which one can swap excitation between the two levels. A full excitation swap is realized by setting Ωt = π, leading to \({U}_{{{{\rm{TLS}}}}}^{\prime}=-{{{\rm{i}}}}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}\theta }{\left|i\right\rangle }{\left\langle \, j\right|}-{{{\rm{i}}}}{{{{\rm{e}}}}}^{{{{\rm{i}}}}\theta }{\left|\,{j}\right\rangle }{\left\langle {i}\right|}\). Note that the phase of the Rabi drive can be controlled by the phase of the parametric drive θ.

Phase calibration of the QuAND gate

From equation (5), the coupler-assisted iSWAP11−20 operation can be expressed by a unitary \(-{{{\rm{i}}}}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}\theta }{\left|{11}\right\rangle }{\left\langle {20}\right|}-{{{\rm{i}}}}{{{{\rm{e}}}}}^{{{{\rm{i}}}}\theta }{\left|{20}\right\rangle }{\left\langle {11}\right|}\), where the phase θ is controlled by the parametric drive. Because the ancilla state \({\left|{20}\right\rangle}\) is used only for temporary storage, the individual phase is irrelevant and only the relative phase between two iSWAP11−20 gates matters. Two consecutive iSWAP-like gates (with phases θ1 and θ2) cause the state evolution to follow \({{\left|11\right\rangle }\to -{{{\rm{i}}}}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}{\theta }_{1}}{\left|{20}\right\rangle }\to -{{{{\rm{e}}}}}^{{{{\rm{i}}}}({\theta }_{2}-{\theta }_{1})}{\left|{11}\right\rangle}}\), restoring the population distribution in the end but with an additional phase factor. Viewed in the computational subspace (\({\left|{00}\right\rangle}\), \({\left|{01}\right\rangle}\), \({\left|{10}\right\rangle}\), \({\left|{11}\right\rangle}\)), the extra phase on \({\left|{11}\right\rangle}\) becomes a conditional phase, which is unwanted if our goal is to retain an identity operation as prescribed in the QuAND scheme. The conditional phase may be eliminated by letting θ2 − θ1 = π. However, in practical implementations, there are a few more details to consider. First, the \({\left|{20}\right\rangle}\) state is at a different energy from the \({\left|{11}\right\rangle}\) state, and an additional phase accumulates during the idling period between the two iSWAP11−20 gates. After the second iSWAP11−20 gate, this phase shows up as a conditional phase on \({\left|{11}\right\rangle}\). Besides idling, an extra phase may also accumulate during the period of frequency modulation. Fortunately, we do not need to measure each of these contributions for correction. These phases can be grouped together as a total conditional phase, which we can calibrate away by sweeping θ2 (assuming an arbitrary θ1) while measuring the final conditional phase in the conditional Ramsey experiment. Further discussion on the calibration procedures is provided in SupplementarySection V.