Introduction

Following the discovery of superconductivity in the cuprates1 and the seminal work by Anderson2, the theoretical efforts to understand high-temperature superconductivity have been focusing to a large extent on a simple model: the one-band Hubbard model3,4,5. However, superconducting cuprates need to be doped, and the doped holes go into the oxygen orbitals6,7,8. This requires a more elaborate multi-band model such as the three-orbital Emery model9. If at all, the Hubbard model may mimic the physics of the Zhang-Rice singlet10 between the moment on the copper sites and the oxygen holes.

The recent discovery of superconductivity in Sr0.2Nd0.8NiO2 by Li et al.11 marked the beginning of a new, a nickel age of superconductivity, ensuing a plethora of experimental and theoretical work; see, among others, refs 12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34. Similar as for the cuprates, the basic structural elements are NiO2 square lattice planes, and Ni has the same formal 3d9 electronic configuration.

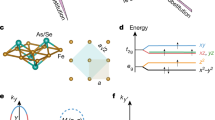
But at second glance, there are noteworthy differences, see Fig. 1a. For the parent compound NdNiO2, density functional theory (DFT) calculations show, besides the Ni \({d}_{{x}^{2}-{y}^{2}}\) orbital, additional bands around the Fermi level EF15,20,21,35 that are of predominant Nd-5d character and overlap with the former. Note that the Nd-5d bands in Fig. 1a extend below EF despite their centre of gravity being considerably above EF.

Fig. 1: Energy levels and phase diagram.
figure 1

a Energy levels comparing CaCuO2 and NdNiO2, with the DFT bandstructure as a background. b Phase diagram TC vs. Sr-doping as calculated in DΓA together with the hitherto only experimental point: 15 K for 20% Sr-doping11. In the blue-shaded region, a one-band Hubbard model description is possible with its doping given on the upper x-axis.

Full size image

Such bands or electron pockets have the intriguing effect that even for the parent compound NdNiO2, the Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital is hole doped, with the missing electrons in the Nd-5d pockets. In other words, the parent compound NdNiO2 already behaves as the doped cuprates. First calculations16,19,27 for superconductivity in the nickelates that are valid at weak interaction strength hence started from a Fermi surface with both, the Nd-5d pockets and the Ni-\({d}_{{x}^{2}-{y}^{2}}\) Fermi surface. Such a multi-orbital nature of superconductivity has also been advocated in refs 18,29.

There is additionally the Nd-4f orbital which in DFT spuriously shows up just above the Fermi energy. But these 4f orbitals will be localised which can be mimicked by DFT + U or by putting them into the core, as has been done in Fig. 1a. Choi et al.32 suggest a ferromagnetic, i.e., anti-Kondo coupling of these Nd-4f with the aforementioned Nd-5d states. A further striking difference is that the oxygen band is much further away from the Fermi level than for the cuprates, see Fig. 1a. Vice versa, the other Ni-3d orbitals are closer to the Fermi energy and slightly doped because of their hybridisation with the Nd-5d orbitals.

This raises the following issues: which orbitals are depopulated upon Sr doping NdNiO2; the validity of a single-orbital description in the superconducting doping range; the doping range in which SrxNd1−xNiO2 is actually superconducting; and the upper superconducting transition temperature TC.

Addressing these points calls for a proper treatment of electronic correlations since e.g., the formation of Hubbard side bands has the potential to alter the orbitals that host the holes induced by Sr doping. In a material-specific, ab initio way this can be done using DFT + dynamical mean-field theory (DMFT)36 and several groups have done such DFT + DMFT studies25,26,28,33,34. Most of these focus on the undoped parent compound and arrive at a picture that the main players are the Ni \({d}_{{x}^{2}-{y}^{2}}\) orbital plus A (and Γ) pocket.

However, if we further Sr-dope the system this picture must break down. If we have e.g., two holes in the Ni orbitals as for LaNiO2H28, it is clear that because of Hund’s rule coupling we need at least two Ni orbitals. Hence somewhere inbetween the undoped parent compound and the high Sr-doping regime, there must be a crossover from a Ni-\({d}_{{x}^{2}-{y}^{2}}\)-orbital picture plus hole pockets to a multi-Ni-orbital picture. Whether this crossover happens before, within or after the superconducting Sr-doping regime is one of the key questions for identifying the minimal model of superconductivity in nickelates.

In this paper, we show that, if we properly include electronic correlations by DMFT, up to a Sr-doping x of about 30%, the holes only depopulate the Ni-3\({d}_{{x}^{2}-{y}^{2}}\) and Nd-5d bands. Only for larger Sr-dopings, holes are doped into the other Ni-3d orbitals, necessitating a multi-orbital description. The hybridisation between the Ni-3\({d}_{{x}^{2}-{y}^{2}}\) and Nd-5d orbitals as calculated from the DFT-derived Wannier Hamiltonian is vanishing. We hence conclude that up to a Sr-doping of around 30% marked as dark blue in Fig. 1b, a single Ni-3\({d}_{{x}^{2}-{y}^{2}}\) band description as in the one-band Hubbard model is possible. However, because of the Nd-5d pocket(s), which acts like an electron reservoir and otherwise hardly interacts, only part of the Sr-doping [lower x-axis of Fig. 1b] goes into the Ni-3\({d}_{{x}^{2}-{y}^{2}}\)-band [upper x-axis], cf. Supplementary Note 2 for the functional dependence. We also take small Sr-doping out of the blue-shaded region since for such small dopings there is, besides the Nd-5d A-pocket, the Γ-pocket which interacts with the Nd-4f moments ferromagentically32 and might result in additional correlation effects. At larger doping and when including the Nd-interaction in DMFT the Γ-pocket is shifted above EF, see Fig. 2 below and e.g., refs 16,25,28,32.

Fig. 2: DFT+DMFT spectral function.
figure 2

a–c DFT + DMFT k-integrated spectral function A(ω) of SrxNd1−xNiO2 at 0%, 20% and 30% Sr-doping, orbitally resolved for the Nd-5d and Ni-3d orbitals. d DFT + DMFT k-resolved spectral function A(ω) for Sr0.2Nd0.8NiO2. e Zoom-in of d. The DFT bands are shown as (white) lines for comparison. Around the Fermi level there is a single Ni-3\({d}_{{x}^{2}-{y}^{2}}\) orbital, as in the one-band Hubbard model with an additional Nd-5dxy pocket around the A-point as a hardly hybridising bystander.

Full size image

Figure 1b further shows the superconducting critical temperature TC of the thus derived and doped Hubbard model, calculated by a method that is appropriate in the strong coupling regime: the dynamical vertex approximation (DΓA37). The agreement between DΓA and experiment in Fig. 1b is reasonable given that the experimental TC can be expected to be lower because of e.g., impurity scattering and the theoretical one is somewhat overestimated (The back coupling of the particle–particle channel to the particle-hole and transversal particle-hole channel is not included. While a (tiny) hopping tz in the z-direction is necessary to overcome the Mermin-Wagner theorem, somewhat larger tz’s may suppress TC38,39).

Results and discussion

DDFT + DMFT multi-orbital calculations

Let us now discuss these results in more detail. We start with a DFT calculation [cf. Supplementary Note 1] which puts the Nd-4f orbitals just above EF. But since their hybridisation with the Ni-3\({d}_{{x}^{2}-{y}^{2}}\) orbital is weak40, \(| {V}_{{x}^{2}-{y}^{2},4f}| =25\)meV, see Supplementary Note 2, they will localise and not make a Kondo effect. This localisation can be described e.g., by the spin-splitting in DFT+U, or by including the Nd-4f states in the core. It leaves us with a well defined window with just five Nd-5d and five Ni-3d around the Fermi energy. For these remaining ten orbitals we do a Wannier function projection (see Supplementary Note 2) and subsequent DMFT calculation with constrained random phase approximation (cRPA) calculated inter-orbital interaction \(U^{\prime} =3.10\)eV (2.00 eV) and Hund’s exchange J = 0.65 eV (0.25 eV) for Ni (Nd)28. Figure 2 presents the calculated DMFT spectral function for these ten bands. Let us first concentrate on Sr0.2Nd0.8NiO2 for which also the k-resolved spectral function on the right hand side is shown. Clearly in DMFT there is a single, compared to the DFT strongly renormalized Ni-3d band of \({d}_{{x}^{2}-{y}^{2}}\) character crossing EF = 0, see the zoom in Fig. 2e. Besides, there is also a pocket around the A-point of predominately Nd-5dxy character, but the Γ-pocket is shifted above EF, cf. Supplementary Notes 3 and 4 for other dopings.

Hence, we have two bands of predominately Ni-3\({d}_{{x}^{2}-{y}^{2}}\) and Nd-5dxy character. Their hybridisation is zero, see Supplementary Table III, which can be inferred already from the lack of any splitting around the DFT crossing points in Fig. 2d, e. There is some hybridisation of the Nd-5dxy with the other Ni-bands, which results in minor spectral weight of Nd-5dxy character in the region of the other Ni-3d bands at −0.5 to −2.5 eV in Fig. 2a–c and vice-versa of the Ni-3\({d}_{{z}^{2}}\) orbital between 1 and 3 eV. This admixing is however so minor, that it can be described by properly admixed, effective orbitals that are away from the Fermi energy, without multi-orbital physics.

If we study the doping dependence in Fig. 2a–c, we see that with Sr-doping all bands move upwards. More involved and beyond a rigid-band picture, also the Ni-3\({d}_{{x}^{2}-{y}^{2}}\) band becomes less and less correlated. The effective mass enhancement or inverse quasiparticle weight changes from m*/m = 1/Z = 4.4 for the undoped compound to m*/m = 2.8 at 20% Sr-doping to m*/m = 2.5 at 30% Sr-doping. The Hubbard bands gradually disappear.

At 30% Sr-doping we are in the situation that the other Ni-3d bands are now immediately below the Fermi energy. Hence around this doping it is no longer justified to employ a Ni-\({d}_{{x}^{2}-{y}^{2}}\)-band plus Nd-dxy-pocket around A picture to describe the low-energy physics. The other Ni-3d orbitals become relevant. Because of the weak hybdization, the Nd-dxy-pocket only acts as an electron reservoir, which changes the doping of the Ni-\({d}_{{x}^{2}-{y}^{2}}\)-band from the lower x-axis in Fig. 1b to the upper x-axis.

For this \({d}_{{x}^{2}-{y}^{2}}\)-band we have done a separate Wannier function projection which results in the hopping parameters t = 395 meV, \(t^{\prime} =-95\) meV, t″ = 47 meV between first-, second-, and third-nearest neighbors on a square lattice. We employed the onsite interaction U = 3.2 eV = 8t which is slightly larger than the cRPA zero frequency value [U = 2.6 eV16,20] to mimic the frequency dependence, as well as beyond cRPA contributions41. In the Supplementary Note 5 we present further calculations within a realistic range of U values. The hopping parameters in the z-direction are negligibly small tz = 34 meV, leaving us with a—to a good approximation—two-dimensional one-band Hubbard model.

T C in DΓA

This two-dimensional one-band Hubbard model with the properly translated doping according to Fig. 1b can now be solved using more sophisticated, numerically expensive methods such as the DΓA37. DΓA starts from a local irreducible vertex, which depends on three frequencies and is calculated at DMFT convergence. From this, DΓA builds non-local vertices and self-energies through ladder or parquet diagrams. The types of diagrams are similar as in the random phase approximation (RPA) or fluctuation exchange (FLEX), but the important difference is the starting vertex which is non-perturbative. As a consequence all local DMFT correlations are included as well non-local spin-, charge- or superconducting fluctuations. This way, among others, (quantum) critical exponents, pseudogaps and superconductivity in the one-band Hubbard model can be calculated37. Applying ladder DΓA to cuprates yields quite reasonable TC’s42, giving us some confidence to now explore the largely unknown nickelates. As a matter of course effects beyond the Hubbard model, such as disorder and phonons or a strengthening of charge fluctuations43 by non-local interactions which all are also considered to be of some relevance for superconductivity44 are not included. Studying a (tetragonal) rotational symmetry breaking45 would require a full parquet DΓA or an eigenvalue analysis like we do for d-wave superconductivity here.

Figure 3 shows the thus obtained DΓA Fermi surfaces at different dopings and two different temperatures. For the superconducting Sr0.2Nd0.8NiO2, which corresponds to \(n_{d_{x^{2}-y^{2}}}=0.822\) electrons per site in the Ni-\(d_{x^{2}-y^{2}}\)-(Wannier)-band, we have a well defined hole-like Fermi surface, whereas for \(n_{d_{x^2-y^2}}=0.9\) and, in particular for \({n}_{{d}_{{x}^{2}-{y}^{2}}}=0.95\), we see the development of Fermi arcs induced by strong antiferromagnetic spin fluctuations. The A = (π, π, π)-pocket is not visible in Fig. 3 because it is only included through the effective doping in the DΓA calculation. In any case it would be absent in the kz = 0 plane and only be visible around kz = π.

Fig. 3: DΓA spectrum.
figure 3

DΓA k-resolved spectrum at the Fermi energy for T = 0.02t = 92 K (upper panels) and T = 0.01t = 46 K (lower panels) and four different dopings \({n}_{{d}_{{x}^{2}-{y}^{2}}}\) of the Ni-\({d}_{{x}^{2}-{y}^{2}}\)-band (left to right).

Full size image

Whereas the Ni-3\({d}_{{x}^{2}-{y}^{2}}\)-band is strongly correlated and has a Fermi surface that is prone to high-TC superconductivity, the A-pocket is weakly correlated and hardly hybridises with the former. Nonetheless for some physical quantities, different from superconductivity, it will play a role. For example, the A-pocket will give an electron-like (negative) contribution to the Hall coefficient. Experimentally, the Hall coefficient11 is large and electron-like (negative) for NdNiO2, whereas it is smaller and even changes its sign from negative (electron-like) to positive (hole-like) below 50 K for Sr0.2Nd0.8NiO2. This doping dependence at low temperatures is strikingly different to the cuprates and can be naturally explained from the balance between a 3\({d}_{{x}^{2}-{y}^{2}}\) hole-contribution (like for cuprate) and an additional electron-like A-pocket contribution. In Fig. 3, we observed a pseudogap behaviour in the underdoped region. This should reduce the hole contribution somewhat as in underdoped cupates46. We expect hence that the electron-like A-pocket contribution wins in the low doping regime, but the 3\({d}_{{x}^{2}-{y}^{2}}\) hole-like contribution might well dominate for larger dopings, qualtitatively explaining the sign change of the Hall coefficient.

Moreover, in Fig. 3 we further see that for T = 92 K = 0.02t, we have a strong scattering at the antinodal point k = (π, 0), whereas at the lower temperature T = 46 K = 0.01t, we have a more well defined band throughout the Brillouin zone. This indicates that the 3\({d}_{{x}^{2}-{y}^{2}}\) hole contribution is suppressed at higher temperatures, whereas the uncorrelated A-pocket contribution essentially remains the same. This possibly explains why the Hall coefficient changes sign11 when increasing temperature for Sr0.2Nd0.8NiO2.

At the temperatures of Fig. 3, SrxNd1−xNiO2 is not yet superconducting. But we can determine TC from the divergence of the superconducting susceptibility χ, or alternatively the leading superconducting eigenvalue λSC. These are related through, in matrix notation, χ = χ0/[1 − Γppχ0]. Here χ0 is the bare superconducting susceptibility and Γpp the irreducible vertex in the particle–particle channel calculated by DΓA; λSC is the leading eigenvalue of Γppχ0. If λSC approaches 1, the superconducting susceptibility is diverging.

In Fig. 4 we plot this λSC vs. temperature, and see that it approaches 1 at e.g., T = 36 K = 0.008t for \({n}_{{d}_{{x}^{2}-{y}^{2}}}=0.85\). But outside a narrow doping regime between \({n}_{{d}_{{x}^{2}-{y}^{2}}}=0.9\) and 0.8 it does not approach 1. There is no superconductivity. Let us also note that the phase transition is toward d-wave superconductivity which can be inferred from the leading eigenvector corresponding to λSC.

Fig. 4: Superconducting eigenvalues.
figure 4

Leading DΓA superconducting eigenvalue λSC vs. temperature T. The superconducting TC corresponds to λSC → 1.

Full size image

Altogether, this leads to the superconducting dome of Fig. 1b. Most noteworthy Sr0.2Nd0.8NiO2 which was found to be superconducting in experiment11 is close to optimal doping \({n}_{{d}_{{x}^{2}-{y}^{2}}}=0.85\) or Sr0.16Nd0.84NiO2. Our results call for a more thorough investigation of superconductivity in nickelates around this doping, which is quite challenging experimentally12,13,14.

Besides a slight increase of TC by optimising the doping, and further room of improvement by adjusting \(t^{\prime}\) and t″, our results especially show that a larger bandwidth and a somewhat smaller interaction-to-bandwidth ratio may substantially enhance TC, see Supplementary Fig. 7, qualitatively similar as in fluctuation exchange (FLEX) calculations16. One way to achieve this is compressive strain, which enlarges the bandwidth while hardly affecting the interaction. Compressive strain can be realised by e.g., growing thin nickelate films on a LaAlO3 substrate with or without SrTiO3 capping layer, or by Ca-doping instead of Sr-doping for the bulk or thick films. Another route is to substitute 3d Ni by 4d elements, e.g., in Nd(La)PdO2 which has a similar Coulomb interaction and larger bandwidth17,47.

Note added: In an independent DFT+DMFT study Leonov et al.48 also observe the shift of the Γ-pocket above EF with doping for LaNiO2 and the occupation of further Ni 3d orbitals besides the 3\({d}_{{x}^{2}-{y}^{2}}\) for large (e.g., 40%) doping.

Second note added: Given that our phase diagram Fig. 1b has been a prediction with only a single experimental data point given, the most recently experimentally determined phase diagram49,50 turned out to be in very good agreement. In particular if one considers, as noted already above, that the theoretical calculation should overestimate TC, while the exerimentally observed TC is likely suppressed by extrinsic contributions such as disorder etc. Supplementary Note 6 shows a comparison, which corroborates the modelling and theoretical understanding achieved in the present paper.

Third note added: In recent single particle tunnelling measurements51, the authors observed the dominant d-wave and the additional s-wave component of the superconducting gap function, which is apparently consistent with our scenario: the dominant d-wave single orbital system with additional Fermi pockets.

Method

Density functional theory

We mainly employ the WIEN2K program package52 using the PBE version of the generalised gradient approximation (GGA), a 13 × 13 × 15 momentum grid, and RMTKmax = 7.0 with a muffin-tin radius RMT = 2.50, 1.95 and 1.68 a.u. for Nd, Ni and O, respectively. But we also double checked against VASP53, which was also used for structural relaxation (a = b = 3.86 Å, c = 3.24 Å)40, and FPLO54, which was used for Fig. 1a and Supplementary Fig. 1. The Nd-4f orbitals are treated as open core states if not stated otherwise.

Wannier function projection

The WIEN2K bandstructure around the Fermi energy is projected onto maximally localised Wannier functions55 using WIEN2WANNIER56. For the DMFT we employ a projection onto five Ni-3d and five Nd-5d bands; for the parameterisation of the one-band Hubbard model we project onto the Ni-3\({d}_{{x}^{2}-{y}^{2}}\) orbital. For calculating the hybridisation with the Nd-4f, we further Wannier projected onto 17 bands, with the Nd-4f states now treated as valence bands in GGA.

Dynamical mean-field theory

We supplement the five Ni-3d plus five Nd-5d orbital Wannier Hamiltonian by a cRPA calculated Coulomb repulsions28 \(U^{\prime} =3.10\)eV (2.00 eV) and Hund’s exchange J = 0.65 eV (0.25 eV) for Ni (Nd or La). The resulting Kanamori Hamiltonian is solved in DMFT36 at room temperature (300 K) using continuous-time quantum Monte Carlo simulations in the hybridisation expansion57 implemented in W2DYNAMICS58. The maximum entropy method59 is employed for the analytic continuation of the spectra.

Dynamical vertex approximation

For calculating the superconducting TC, we employ the dynamical vertex approximation (DΓA), for a review see ref. 37. We first calculate the particle–particle vertex with spin-fluctuations in the particle-hole and transversal-particle hole channel, and then the leading eigenvalues in the particle–particle channel, as done before in ref. 42. This is like the first iteration for the particle–particle channel in a more complete parquet DΓA37.