Introduction

High-transition temperature superconductors (high-Tc) such as copper oxides and iron pnictides have plethora of electronic phases that emerge from their three-dimensional (3D) antiferromagnetic (AF) ordered parent compounds.1,2,3,4,5,6 While the microscopic mechanism of such emergence remains elusive, it is generally believed that the formation of different phases results from a subtle balance among the spin, charge, lattice and orbital degrees of freedom. Therefore, by using an external probe such as pressure to tune this balance, one can manipulate different emergent electronic phases in high-Tc superconductors, and understand their relationship with superconductivity.

In the case of iron pnictides such as BaFe2(As1−xPx)2,7,8 where the parent compound BaFe2As2 has a collinear AF order below TN preceded by a tetragonal-to-orthorhombic lattice distortion at Ts with Ts ≥ TN (Fig. 1a–c),4,5,6 optimal superconductivity with Tc ≈ 30 K emerges upon complete suppression of the 3D AF order and Ts by increasing x to 0.39,10 or hydrostatic pressure.11,12,13 From transport, magnetic penetration depth, and heat capacity measurements, a quantum critical point (QCP), where a nonzero temperature phase transition is suppressed continuously to zero temperature, has been identified near x ≈ 0.3.10 Although initial nuclear magnetic resonance (NMR) measurements14 suggest that the observed QCP arises from the gradual suppression of the collinear AF order near x = 0.3, neutron diffraction and recent NMR measurements indicate that the AF transition in BaFe2(As1−xPx)2 disappears in a weakly first-order fashion near optimal superconductivity with an avoided magnetic QCP.15,16,17 On the other hand, a two-dimensional (2D) nematic phase, whose electronic properties break the in-plane rotational symmetry but preserve the translational symmetry of the underlying lattice,18 has been theoretically postulated below Ts19,20,21 and experimentally observed in different families of iron pnictides.22,23,24,25,26,27 In particular, elastoresistivity measurements in BaFe2(As1−xPx)2 reveal a diverging nematic susceptibility near x ≈ 0.3, suggesting a nematic origin for the observed QCP.28,29

Fig. 1
figure 1

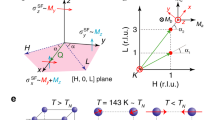
Summary of the electronic phase diagram and uniaxial pressure effect on transport data in BaFe2(As1−xPx)2. a The crystal structure of BaFe2(As1−xPx)2. The purple, silvery, and blue balls indicate Fe, As/P, and Ba positions, respectively. b The collinear AF structure of BaFe2As2, which requires orthorhombic lattice distortion. c The corresponding reciprocal space, where AF Bragg peaks occur at (1, 0, L) with L = 1, 3, …. d Schematic diagrams of the FeAs tetrahedron, showing the (As, P) height to iron plane is hAs/P = 1.304(7) Å and the nearest in plabe Fe–Fe atom distance is 2.774(2) Å, respectively, for BaFe2(As0.70P0.30)2 in 300 K. e By applying a uniaxial pressure along the c-axis, pnictogen height is hAs/P = 1.306(9) Å and the in-plane Fe–Fe atom distance increases to 2.778(3) Å correspondingly. f Temperature dependence of in-plane resistance for pressures up-to 480 MPa along the c-axis of BaFe2(As0.70P0.30)2 crystal. g The electronic phase diagram of BaFe2(As1−xPx)2, where AF, superconductivity, Fermi liquid, Non-Fermi liquid, and a QCP (red dot) are marked. The yellow and green colors represent the values of n in temperature dependence of the resistivity exponent.10 Arrow marks the position in the phase diagram of the compound measured in this work

Full size image

Although optimal superconductivity can be achieved by a continuous suppression of the finite temperature structural phase transition Ts and magnetic phase transition TN to zero temperature through increasing P-doping in BaFe2(As1−xPx)2 (Fig. 1a-c),9 it is rather difficult to study the interplay between the nematic/magnetic order and superconductivity due to the sensitive P-doping dependence of structural and magnetic transitions near the optimal superconductivity.10 Therefore, it is unclear if the nematic phase, which is associated with Ts, help or compete with superconductivity. Although it has been argued theoretically that nematic fluctuations can enhance superconductivity,30,31 the relationship between static nematic order and superconductivity is still unclear.

One way to resolve this problem is to use uniaxial pressure (strain) as a probe to tune the system toward or away from the optimal superconductivity. In general, Tc in iron based superconductors is related with crystal structural parameters including the height of As/P anion (pnictogen) to the Fe layer hanion = hAs/P (Fig. 1d).32,33,34,35,36 For BaFe2(As1−xPx)2, increasing P-doping concentration is linearly associated with decreasing pnictogen height hAs/P, and reaches optimal superconductivity with Tc ≈ 30 K near hAs/P ≈ 1.30 Å (Fig. 1d).37 From pressure dependence of thermodynamic measurements, it was found that a c-axis uniaxial pressure on BaFe2(As1−xPx)2 corresponds to an increased P-doping level.11,38,39 This means that in the P underdoped regime (x < 0.3), uniaxial pressure along the c-axis will increase Tc and suppress TN, while in the overdoped regime without static AF order (x ≥ 0.3), it will simply suppress Tc (Fig. 1e, f). Since nematic order in iron pnictides occurs below Ts,21 a c-axis aligned uniaxial pressure on the tetragonal structured BaFe2(As0.70P0.30)2 near the optimal superconductivity is not expected to induce static collinear AF order, which is associated with the in-plane orthorhombic lattice distortion (Fig. 1b). For BaFe2(As0.70P0.30)2 near optimal superconductivity,15,16 transport measurements at zero pressure revealed the linear temperature dependence of the resistivity above Tc [R(T) = R(0) + αTn with n ≈ 1, where R(T) is resistivity, α and n are fitting parameters.] (Fig. 1g).10 Application of a c-axis pressure is expected to push the phase diagram into the overdoped regime, and should not alter dramatically the linear temperature dependence of the resistivity.

Surprisingly, we find that a c-axis aligned uniaxial pressure on BaFe2(As0.70P0.30)2 not only suppresses Tc (Fig. 1f), but also induces resistivity deviation from the zero pressure linear temperature dependence (Fig. 2). Figure 3 shows uniaxial pressure dependence of Tc, suggesting an approximate linear relationship between the applied pressure and reduction in Tc below ~ 280 MPa. Upon further increasing uniaxial pressure, the reduction in Tc reduces, while the temperature where resistivity deviates from the linear temperature dependence increases (Fig. 3). Our neutron diffraction experiments on BaFe2(As0.70P0.30)2 reveal that the deviation in resistivity from the linear temperature dependence in Figs. 2, 3 arise from a pressure-induced collinear AF order with TN > Tc (Figs. 4, 5). This is difficult to understand within the conventional Fermi surface nesting picture,40 where a c-axis pressure is expected to induce pnictogen height reduction, promote electron itinerancy, and drive the system to the P-overdoped side with reduced Tc and no static AF order. Since the collinear AF order in iron pnictides has to be associated with the orthorhombic distortion of the underlying lattice (Fig. 1b),3,4,5,6 our results provide the compelling evidence that a c-axis pressure actually induces an in-plane C4 symmetry breaking field in the underlying lattice and drives the system into a nematic ordered phase. To understand this phenomenon, we carried out neutron diffraction experiments on single crystals with zero and ~ 400 MPa c-axis pressure. Our Rietveld analysis reveals that the dominant effect of a c-axis pressure is to suppress the c-axis and expand the in-plane lattice constants, and has limited effect on the average (As, P) pnictogen height hAs/P (Fig. 1d, e, and Table 1). This is true even though As and P atoms occupy distinct positions in BaFe2(As1−xPx)2.41 Based on the refined crystal structures at zero and finite pressure, we use a combination of density functional theory and dynamical mean field theory (DFT + DMFT)42 to study the effect of a c-axis pressure on the magnetic property of BaFe2(As0.70P0.30)2, and find that strong magnetoelastic coupling with the in-plane lattice is the driving force for the c-axis pressure induced the long-range static AF order. As the pressure-induced nematic order with TN, Ts > 30 K increases with increasing pressure (Figs. 2–5), we conclude that the nematic order is competing with superconductivity and therefore needs to be taken into account to understand the electronic properties of iron pnictides.

Fig. 2
figure 2

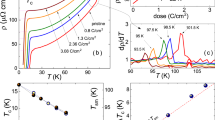
Summary of pressure dependence of resistivity. Temperature dependence of normalized in-plane resistance for different pressures along the c-axis of BaFe2(As0.70P0.30)2 crystal using automated uniaxial pressure device described in ref.51. a P = 0. The arrow indicates Tc at ρ = 0. b P = 10 MPa. c P = 20 MPa. d P = 40 MPa. e P = 60 MPa. f P = 80 MPa. g P = 100 MPa. h P = 140 MPa. i P = 180 MPa. j P = 280 MPa. k P = 380 MPa. l P = 480 MPa. The inset shows temperature derivative of the in-plane resistance, which reveals more clearly the deviation from linear temperature dependence. The black lines are the linear fits for high temperature data (80–120 K) and the vertical dashed green lines mark the temperature, where the observed resistance deviates from the linear temperature dependence

Full size image
Fig. 3
figure 3

The c-axis pressure dependence of Tc and TN as determined from transport measurement. The c-axis uniaxial pressure dependence of Tc at ρ = 0 and the deviation temperatures from the linear temperature resistance. The error bars are the superconducting transition widths with Pc = 0 and 480 MPa. The error bars for TN are estimated by using temperature derivative of the resistance data. The red and blue dashed lines are linear fits to the data

Full size image
Fig. 4
figure 4

Summary of neutron scattering results on sample A. The c-axis pressure-induced magnetic signal in sample A carried out at MIRA and HB-1A. a–c Wave vector scans through the (1, 0, 3) magnetic Bragg peak position at different temperatures with zero and finite pressure. The solid lines are Gaussian fits to the data, and the horizontal bars are instrumental resolution. d Wave vector scans along the [H, 0, L] direction with L = 1, 2, 3 at T = 30 K and finite pressure. e Temperature dependence of the magnetic scattering at QAF = (1, 0, 3) for P = Pa and P = 0. All shown data are background-corrected. All vertical error bars represent statistical error (1 s. d.)

Full size image
Fig. 5
figure 5

Summary of neutron scattering results on sample B. Wave vector and temperature dependence of the uniaxial pressure induced magnetic order for sample B. a Temperature dependence of the magnetic scattering at (1, 0, 3) with and without pressure. b–d Wave vector scans along the [H, 0, 3] direction with and without uniaxial pressure at different temperatures. The absence of magnetic scattering at low-temperature (4 K) suggests that superconductivity can completely suppress the pressure induced magnetic order. The solid lines in b and c are Gaussian fits to the data, and the horizontal bars are instrumental resolution. The solid line in a is a guide to the eye. The blue and green vertical dashed lines in a mark TN and Tc, respectively. All vertical error bars represent statistical error (1 s. d.)

Full size image
Table 1 Results of single crystal diffraction experiments on sample A with P = Pa and P = 0
Full size table

Results

Resistivity measurements

We chose to study the effect of a c-axis aligned uniaxial pressure on BaFe2(As0.70P0.30)2 because P-substitution does not introduce significant disorder43,44,45 and is expected to reduce the average pnictogen height linearly similar to c-axis applied pressure.37 Previous transport measurements on BaFe2(As1−xPx)2 single crystals reveal that both the AF order and superconductivity are sensitive to the applied pressure.39 Similar to other electron-doped iron pnictides,46,47,48,49,50 in-plane uniaxial pressure that breaks the C4 symmetry of the underlying lattice enhances the AF order and suppresses superconductivity in underdoped BaFe2(As1−xPx)2. For comparison, a c-axis aligned uniaxial pressure increases Tc and suppresses TN in the underdoped regime, and is expected to only suppress Tc in the optimal/overdoped regime (Fig. 1g).38,39 In addition, a c-axis pressure is also expected to expand the in-plane lattice parameter, akin to negative in-plane pressure.

We first describe c-axis pressure dependence of the resistivity on BaFe2(As0.70P0.30)2. Figure 1f shows pressure dependence of the resistivity near Tc. With increasing pressure from 0 to 480 MPa using a custom designed uniaxial pressure device,51 we see a systematic reduction in Tc from 29.5 to 28.5 K. Figure 2 summarizes temperature dependence of the resistivity as a function of increasing pressure. At zero pressure, we find linear temperature dependence of the resistivity above Tc and below 90 K, confirming previous work.10 With increasing pressure from 0 to 480 MPa, temperature dependence of the resistivity systematically deviates from the linear behavior as marked by the vertical green dashed lines in Fig. 2. This is reminiscent of the situation in BaFe2(As0.71P0.29)2 at ambient condition, where the system orders antiferromagnetically at a temperature above Tc.16 Assuming that the deviation from the linear temperature dependence is due to pressure-induced static AF order at TN, we show in Fig. 3 pressure dependence of Tc and TN. Simple linear fits to the data yield a reduction in Tc of 3.0 ± 0.2 K/GPa, and an increase of TN of 48 ± 2 K/GPa if we ignore the TN = 0 at zero pressure point (Fig. 3). From neutron diffraction experiments described below, we know that c-axis pressure-induced AF ordered moment in BaFe2(As0.70P0.30)2 is vanishingly small compared with that of the parent compound BaFe2As2. Therefore, we do not expect a c-axis pressure will be able to induce observable magnetic ordered moment change in BaFe2As2.

Neutron scattering results

To confirm the results of transport measurements, we have carried out neutron diffraction experiments. Two single crystals of BaFe2(As0.70P0.30)2, labeled A and B, were clamped between two Al plates using a pressure cell. We first carried out triple-axis measurements to determine the effect of uniaxial pressure on magnetic order. In order to determine the effect of c-axis uniaxial pressure on crystalline lattice, we measured many nuclear Bragg peaks in sample A after the triple axis measurements under pressure at room temperature. We then took another crystal from the same batch and put it in the identical pressure cell, and carried out the same diffraction measurement without pressure at room temperature. These two measurements allowed us to determine the effect of c-axis pressure on the atomic positions and lattice parameters of BaFe2(As0.70P0.30)2.

Figure 4 summarizes the triple-axis neutron scattering results at zero and finite a c-axis uniaxial pressure on sample A. At zero pressure, the sample has no static AF order at T = 29 and 6 K as shown in wave vector scans along the [H, 0, 3] direction through the magnetic Bragg peak position at (1, 0, 3) (Fig. 4a, b). Upon application of a c-axis aligned uniaxial pressure Pa, we find temperature-dependent peaks at (1, 0, 3) (Fig. 4a–c). The solid lines in Fig. 4a–c are Gaussian fits to the data, which give the static spin–spin correlation lengths of 220 ± 30 Å, indicating pressure-induced long-range magnetic order. To determine the spin arrangements in the pressure-induced magnetic phase, we measured magnetic Bragg peaks at different L positions along the [H, 0] direction. Figure 4d shows wave vector scans along the [H, 0] direction at L = 1, 2, 3. For collinear AF order in underdoped BaFe2(As1−xPx)2, we expect magnetic Bragg peaks at L = 1, 3 and no magnetic scattering at L = 2.4,5,6 Figure 4d shows that the magnetic scattering around (1, 0, 3) is about 3.1 times of that at (1, 0, 1), and no magnetic signal at (1, 0, 2). These results are consistent with the collinear AF order in underdoped BaFe2(As1−xPx)2.16 By normalizing the magnetic Bragg peak intensity with a weak nuclear Bragg peak, we estimate that the pressure-induced magnetic ordered moment is about 0.1 μB/Fe. Figure 4e compares temperature dependence of the (1, 0, 3) scattering at zero (P = 0) and finite (P = Pa) c-axis pressure. While the scattering has no temperature dependence at zero pressure consistent with no magnetic order, its behavior at Pa is similar to those of underdoped BaFe2(As1−xPx)2 with TN ≈ 55 K, where the reduction of magnetic scattering below Tc is due to the competition of superconductivity with static AF order.16

Assuming that the temperature where resistivity deviates from the linear temperature dependence in c-axis pressured sample signals the start of static AF order, we compare TN measured by neutron scattering in Figs. 3, 4 determined from transport measurements and find Pa ≈ 400 MPa. The estimated Pa is consistent with the observed reduction in Tc as seen in magnetic scattering intensity reduction in Fig. 4e, although Tc of the sample can only be approximately determined by such measurement. To accurately determine the effect of c-axis uniaxial pressure on the pnictogen height hAs/P and lattice parameters of BaFe2(As0.70P0.30)2, we measured 30 Bragg peaks with P = Pa and repeated the same measurement without pressure at room temperature using HB-3A four circle diffractometer. The Rietveld analysis of the single crystal diffraction data reveal that the major effect of a P ≈ 400 MPa pressure is to suppress the c-axis and expand the in-plane lattice parameters without affecting much the average pnictogen height hAs/P (Table 1).

To determine the uniaxial pressure dependence of the magnetic order, we carried out neutron scattering measurements on sample B under pressure P = Pb < Pa. Figure 5a shows temperature dependence of the magnetic scattering at (1, 0, 3) at zero and P = Pb. Similar to sample A, we find that uniaxial pressure induced magnetic order first appears below TN ≈ 42 K, competes with superconductivity below Tc, and is completely suppressed below 10 K. The lower TN in sample B suggests Pb ≈ 40 MPa based on transport measurements in Fig. 3. Figure 5b–d compare zero and finite pressure (P = Pb) wave vector scans around (1, 0, 3) at different temperatures. From these scans, we estimate that pressure induced AF order has in-plane and c-axis spin–spin correlation lengths of about 120 and 160 Å, respectively. These results are consistent with those described in Fig. 4, revealing that a c-axis aligned uniaxial pressure spontaneously induces the collinear AF order with TN > 30 K.

DFT + DMFT calculation

Our observation suggests that the magnetic properties of BaFe2(As0.70P0.30)2 is very sensitive to small structure changes induced by the c-axis pressure at the optimal P-doping, signaling a large magnetoelastic coupling. Earlier DFT calculations52 of the LaFeAsO parent compound revealed a strong dependence of the ordered magnetic moment on the As height. However, DFT calculations consistently overestimate the Fe ordered magnetic moment.53 Although DFT + DMFT calculations can accurately reproduce the experimental ordered magnetic moments of Fe atoms in a large numbers of iron-based compounds with the same Hubbard U and Hund’s coupling J as used in the current study,53 the dependence of the Fe magnetic moment on the As height has not been carefully studied by DFT + DMFT calculations.

To determine the magnitude of the magnetoelastic coupling and understand the unusual behavior under c-axis pressure, we use a DFT + DMFT theory to study BaFe2(As0.70P0.30)2.42 In the DFT + DMFT calculations, the electronic charge was computed self-consistently on DFT + DMFT density matrix. The quantum impurity problem was solved by the continuous time quantum Monte Carlo method,54,55 at a temperature of 72.5 K if not otherwise specified, and with a Hubbard U = 5.0 eV and Hund’s rule coupling J = 0.7 eV in the AF state.51,53,56 The experimental lattice constants of optimal P-doped BaFe2(As0.7P0.3)2, a = b = 5.5406 Å and c = 12.761 Å8 are used in the calculations while the internal As/P position zAs/P [where hAs/P = (zAs/P − 0.25)c] is varied from 0.349 to 0.347 in order to determine the (theoretical) critical As/P position/height. In the other set of calculations, the effect of c-axis pressure on the lattice is taken into account by expanding the in-plane lattice constant a by 1% and varying the internal As/P position in the same range whereas the c-lattice constant is fixed to the experimental value to simplify the computation since the As/P position/height and in-plane lattice constant are the dominating factors in determining the magnetic properties. By varying both the As/P height and the in-plane lattice constant, we are able to compute the magnitude of the in-plane and c-axis magnetoelastic coupling constants.

We summarize our DFT + DMFT results in Table 2. Keeping the lattice constant a and c unchanged and varying only the As/P height zAs/P (second row in Table 2), the Fe ordered magnetic moment is 0.138 μB/Fe at zAs/P = 0.349, and quickly decreases to 0.065 μB/Fe at zAs, P = 0.3485, and less than 0.002 μB/Fe at zAs, P = 0.348. The Fe ordered magnetic moment changes at a rate of 11 μB/Å with the hAs/P, much larger than the corresponding value of ~ 3.7 μB/Å in LaFeAsO.52 Therefore, the DFT + DMFT magnetoelastic coupling strength in optimal P-doped BaFe2(As1−xPx)2 is about 3 times stronger than the DFT magnetoelastic coupling strength in LaFeAsO, suggesting correlation-enhanced spin–phonon coupling.57,58,59

Table 2 The DFT + DMFT calculated Fe ordered magnetic moment in the collinear AF state as a function of As/P height zAs/P at the experimental and 1% expanded in-plane lattice constant while keeping the c-lattice constant unchanged
Full size table

Keeping the (As, P) height unchanged at zAs/P = 0.348 as a function of increasing pressure, as seen experimentally in BaFe2(As0.70P0.30)2 (Table 1), increasing the in-plane Fe–Fe spacing by 1% increases the Fe ordered moment to 0.049 μB/Fe, a change rate of 1.2 μB/Å, an order of magnitude smaller than the change rate with respect to the (As, P) height. Therefore, the (As, P) height is the dominating factor in the magnetic properties of the compound. This is further supported by the corresponding calculations at zAs/P = 0.3475 and 0.347 with experimental and 1% expanded in-plane lattice constant (Table 2). With slightly reduced zAs/P, expanding the in-plane Fe–Fe spacing by 1% barely increases the Fe ordered magnetic moment, in strong contrast to the results at zAs/P = 0.348. Therefore, the zAs/P = 0.348 is a critical (As, P) height where the Fe ordered magnetic moment is very sensitive to the in-plane Fe–Fe distance, similar to a previous observation that the Fe ordered magnetic moment shows a large enhancement under in-plane uniaxial pressure near an optimal superconductivity in BaFe2−xTxAs2 (T = Co, Ni).51

Finally, we adopt the experimental results and carry out additional DFT + DMFT calculations in the AF state by expanding the in-plane lattice constant a by 0.5% (from 3.9178 Å to 3.9374 Å) and compressing the c-axis lattice constant by 1% (from 12.761 Å to 12.6347 Å) while the internal As/P position zAs/P is changed from 0.348 to 0.349 in order to keep the As/P height unchanged. The calculations are done at a temperature of 29 K, below the experimental Néel temperature. We find that, without the c-axis pressure, the ordered Fe moment is still less than 0.01 μB, implying no long-range AF magnetic order. However, the long-range AF magnetic order emerges with an ordered Fe moment of 0.10 μB upon applying the aforementioned c-axis pressure. These findings are in good agreement with our experimental observation.

Discussion

Our transport, neutron scattering experiments, and DFT + DMFT calculations on BaFe2(As0.70P0.30)2 reveal that magnetism in this material is particularly sensitive to a c-axis-aligned uniaxial pressure. In previous transport, NMR, magnetic penetration depth, and heat capacity measurements, a QCP has been found at BaFe2(As0.70P0.30)2.10 In particular, differential elastoresistance measurements on BaFe2(As0.70P0.30)2 indicate a diverging nematic susceptibility at T = 0, suggesting that the QCP is nematic in origin.28 Since nematic fluctuations may enhance superconductivity,30,31 it would be important to sort out the relationship between the static nematic phase and superconductivity.

In principle, nematic order of iron pnicitdes is an electronic anisotropic property of the 2D FeAs plane and should couple linearly to anisotropic strain (or pressure) within the FeAs plane in the limit of infinitesimal strains.21 By measuring the rate of change of resistivity anisotropy with respect to the in-plane anisotropic strain, one can determine the nematic susceptibility.28 By contrast, uniaxial pressure along the c-axis, which does not break the in-plane crystalline lattice symmetry, exhibits nonlinear coupling with the nematic order parameter.60 Our surprising discovery that a c-axis aligned strain can actually induce AF order with in-plane symmetry-breaking field suggests that nematic order can also couple to the c-axis pressure via pressure-induced in-plane Fe–Fe distance expansion (Table 1). Although a ~ 400 MPa pressure along the c-axis suppresses the c-axis and expands the in-plane lattice parameters of BaFe2(As0.70P0.30)2, it has negligible effect on the (As, P) height hAs/P (Fig. 1d, e and Table 1). As demonstrated by our DFT + DMFT calculation, this means that BaFe2(As0.70P0.30)2 is at critical doping regime with a critical As/P height where the Fe ordered moment and associated nematic order depend sensitively on the in-plane Fe–Fe distance. In the underdoped region, the As/P height is larger than the critical value of hAs/P ≈ 1.30 Å and the long-range AF order already exists at ambient pressure. Applying a c-axis pressure does not change the AF order dramatically as it does at the optimal doping. On the other hand, in the overdoped region, where the As/P height is below the critical value, a c-axis pressure of similar magnitude should be unable to induce the long-range AF order as shown in Table 2. Further pressure-dependent transport and neutron scattering experiments as a function of P-doping will help us to better understand the quantum critical behavior in iron-based superconductors.

The c-axis pressure-induced AF order we observed in BaFe2(As0.70P0.30)2 is in someways reminiscent of the effect of biaxial strain on the phase transitions in Ca(Fe1−xCox)2As2.61,62 Similar to c-axis uniaxial pressure, biaxial in-plane strain achieved by using the differential thermal expansion between the samples and a rigid substrate affects the c/a ratio of the tetragonal samples but does not break the tetragonal symmetry.61 Instead of decreasing the c/a ratio by applying a c-axis pressure, biaxial in-plane strain in Ca(Fe1−xCox)2As2 increases the c/a ratio and shifts the phase diagram of Ca(Fe1−xCox)2As2 to higher x, without changing the maximum Tc and magnetic phase transition temperature.61 Here, the quantum phase transition between the superconducting tetragonal and AF orthorhombic phases is first-order, and the resulting phase separation into these two phases with different in-plane lattice parameters allows the material to respond to biaxial strain in a continuous fashion.62 For comparison with BaFe2(As0.70P0.30)2, it would be interesting to experimentally determine the biaxial pressure dependence of the iron pnictogen height and Fe–Fe distance, and use DFT + DMFT calculation to see if the experimental phase diagram can be reproduced.

In summary, our neutron scattering results reveal that a moderate uniaxial pressure along the c-axis in BaFe2(As0.70P0.30)2 superconductor can spontaneously induce a three-dimensional stripe AF order with TN > 30 K, while only slightly suppresses Tc. These results indicate a strong magnetoelastic coupling near optimal superconductivity, suggesting a uniaxial pressure-induced nematic phase and stripe AF order competing with superconductivity in BaFe2(As1−xPx)2. These results are also consistent with zero pressure temperature dependence of neutron Larmor diffraction measurements on NaFe1−xNixAs, where the local orthorhombic lattice distortions associated with nematic phase were found to compete with superconductivity.63

Method

Single crystals of BaFe2(As0.70P0.30)2 were prepared using self-flux method.16 Transport measurements were carried out using a commercial physical property measurement system (PPMS) with the standard four-probe method (see Supplementary Information for device used in resistivity measurements). Our neutron scattering experiments were carried out using the MIRA triple-axis spectrometer at Maier–Leibnitz, Garching, Germany,64,65 HB-1A triple-axis spectrometer and HB-3A four circle diffractometer at High Flux Isotope Reactor, Oak Ridge National Laboratory (see Supplementary Information for the description of pressure cell used in neutron scattering experiments and addition data measured on HB-3A). We define the wave vector Q in three-dimensional reciprocal space in Å−1 as Q = Ha* + Kb* + Lc*, where H, K, and L are Miller indices and a* = \(\widehat {{a}}\)2π/a, b* = \(\widehat {{b}}\)2π/b, c* = \(\widehat {{c}}\)2π/c are reciprocal lattice units (r.l.u.). In the low-temperature AF orthorhombic phase of BaFe2(As1−xPx)2, a ≈ 5.57 Å, b ≈ 5.55 Å, and c ≈ 12.80 Å.15 In this notation, we expect magnetic Bragg peaks of the collinear AF structure to occur at (1, 0, L) with L = 1, 3, 5 positions.4,5,6 Near optimal superconductivity, the sample is a tetragonal paramagnet with a = b. Details of DFT + DMFT calculations are described in the Supplementary Information for additional data and analysis.