Magnetic field-induced ferroelectricity in S = 1/2 kagome staircase compound PbCu₃TeO₇

Abstract

Ni₃V₂O₈ is an archetypical multiferroic material with a kagome staircase structure of S = 1 (Ni²⁺) spins whose complex interplay between spin ordering and ferroelectricity has been studied for more than a decade. Here, we report a new kagome staircase compound PbCu₃TeO₇ with Cu²⁺ (S = 1/2) spins that exhibits two Néel temperatures at T_N1 = 36 K and T_N2 = 24 K, and a magnetic field (H)-induced electric polarization (P) below T_N2. Pyroelectric and magnetoelectric current measurements in magnetic fields up to 60 T reveal that for H||c of ~ 8.3 T, a spin-flop transition induces a transverse P||a with a magnitude of 15 µC/m² below T_N2. Furthermore, for a parallel configuration with P//H//a, two spin-flop transitions occur, the first at ~ 16 T with P//a of 14 µC/m², and the second at ~ 38 T, where P disappears. Monte Carlo simulations based on 12 major exchange interactions uncover that a sinusoidal amplitude modulation of the spins occurs along the b-axis below T_N1 and an incommensurate, proper screw-type spin order occurs in the ac-plane below T_N2. The simulation results show that P//a under H//c stems from a spin-flop transition facilitating an ab-plane-type spiral order, while the two successive spin-flop transitions for H//a result in spiral spin orders in the ab- and bc-planes. Based on the experimental and theoretical results, we establish field-induced magnetic and electric phase diagrams for the two H directions, demonstrating that the distorted kagome staircase structure with competing intra–interlayer interactions and lifted frustration creates a plethora of different noncollinear spin textures of S = 1/2 spins that in turn induce electric polarization.

Introduction

Research activities on multiferroics and magnetoelectric (ME) materials have resumed since early 2000s because of the fundamental interests in the physics of strong coupling between spin and lattice degrees of freedom as well as the application potential for numerous low-power electronic devices.^1,2,3,4,5 In particular, magnetic ferroelectrics, in which ferroelectric polarization (P) is induced by spin order, have drawn lots of attention due to the intriguing complexity of the spin textures and magnetoelectric coupling mechanisms, as well as the ability to control 100% of the electric polarization with magnetic ordering. In magnetic ferroelectrics, one route to creating ferroelectricity is via competing magnetic interactions that induce complex nontrivial spin orders. These complex spin orders in turn break spatial inversion symmetry of the combined spin-lattice system and thus induce P.^4,5 For example, ferroelectricity observed in quasi-one-dimensional spin chain compounds MnWO₄,⁶ Ca₃Co_1.04Mn_0.96O₆,⁷ and Lu₂CoMnO₆⁸ can be explained by such complex spin orders induced by the competing nearest and next-nearest neighbor exchange interactions.

Another effective way to realize complex spin orders is to make use of “lifted frustration”. In geometrically frustrated lattice such as triangular, kagome, or spinel structures, the frustration is so complete that no single ordered ground state can occur in theory, giving rise to classical or quantum-spin liquids. However, in real systems, the perfect spin frustration is often lifted by symmetry-reducing lattice distortions that eventually lead to spontaneous spin ordering at finite temperatures. These lattice distortions can directly cause ferroelectricity, or the resulting spin orderings are also sufficiently complex as to induce electric polarization, as occurs, e.g., in Ni₃V₂O₈,^{9,10,11,12,13,14} CuFeO₂,^15,16 CoCr₂O₄¹⁷, and AgCrO₂.¹⁸

Among geometrically frustrated lattices,^6,7,8 the kagome structure has received particular attention since it is a prime candidate for creating quantum-spin-liquid states.¹⁹ Numerous studies^20,21 have mainly focused on the quest for a possible quantum-spin-liquid ground state in the ideal kagome lattices, whereas multiferroic properties have not been extensively studied. Ni₃V₂O₈, however, is a rare example of exhibiting multiferroic behavior in a distorted kagome structure. Here, Ni²⁺ (S = 1) spins organize into a buckled form of the kagome structure, called as the kagome staircase structure. Extensive studies on Ni₃V₂O₈ have now made significant progresses in understanding its intriguing ME coupling and complex phase diagram.^{9,10,11,12,13,14} Upon being cooled, Ni₃V₂O₈ exhibits four magnetic phases below 9.3 K; high- and low-temperature incommensurate (HTI and LTI) and two commensurate ones. Among those, ferroelectricity has been found only in the LTI phase, in which neutron scattering studies^9,12 have revealed stabilization of a spin cycloid structure in the ab-plane. Therefore, the origin of spontaneous P is now understood as coming from the so-called inverse Dzyaloshinskii–Moriya (IDM) mechanism.^22,23,24

In terms of multiferroics/ME properties, the S = 1/2 system containing Cu²⁺ ions has drawn continual interest because strong quantum fluctuation effects expected from the smallest possible spin value may show up in the magnetic and multiferroic properties.^25,26 Moreover, some of the Cu²⁺-containing compounds have high spin ordering temperatures because of their strong superexchange interaction arising from Cu–O–Cu bonding.^27,28 A number of multiferroic/ME compounds with S = 1/2 chains were indeed found; LiCu₂O₂,²⁵ SrCuTe₂O₆,²⁶ CuO,²⁷ CuBr₂,²⁸ LiCuVO₄,²⁹ CuCrO₄,³⁰ CuCl₂,³¹ PbCuSO₄(OH)₂,³² Cu₃Mo₂O₉,³³ α-Cu₂V₂O₇,³⁴ Cu₃Nb₂O₈,³⁵ Cu₃Bi(SeO₃)₂O₂Cl,³⁶ and KCu₃As₂O₇(OD)₃.^37,38 Most of these compounds listed in refs. 25,26,27,28,29,30,31,32,33,34,35,36,37,38 share a common feature of CuO₂ ribbons with edge-sharing CuO₄ square planes. Therefore, the nearest-neighbor spin interaction through the Cu–O–Cu path can compete with the next-nearest neighbor interaction through the Cu–O–O–Cu path, resulting in a cycloidal spin order. Spontaneous P can then be induced by the IDM mechanism.^22,23,24 Moreover, recently known multiferroic compound KCu₃As₂O₇(OD)₃ has a monoclinically distorted kagome structure, which allows long-range spin order with a cycloidal configuration.^37,38 However, to our knowledge, no ME or multiferroic behaviors have been found to date in the staircase kagome spin structure with S = 1/2 Cu²⁺ ions, which could open a new route to find exotic magnetic and multiferroic phenomena due to its unique opportunity of having quantum fluctuation, geometric spin frustration, and competing nearest- and next-nearest spin interaction all in one spin network.

We have recently found that Cu²⁺ (S = 1/2) ions in one of emergent copper tellurium oxides PbCu₃TeO₇,^39,40,41 form the kagome staircase structure. The previous studies of magnetization,³⁹ heat capacity,³⁹ and nuclear magnetic resonance (NMR) studies⁴⁰ have shown that PbCu₃TeO₇ has two antiferromagnetic (AFM) transitions at T_N1 = 36 K and T_N2 = 24 K and a small change in the magnetic susceptibility at T_N3 = 17 K. The Curie–Weiss temperature θ_CW = −150 K obtained from the magnetic susceptibility indicated the presence of moderate spin frustration. In addition, strong interlayer interactions through the Cu–O–Te–O–Cu path were evident in the NMR measurement.⁴⁰ This observation indicates that we should expect not only highly frustrated intralayer spin interactions, but also competing next-nearest exchange interaction via the strong interlayer coupling. Therefore, PbCu₃TeO₇ is a good candidate material for exhibiting the noncollinear spin order and magnetism-induced ferroelectricity.

In this article, we report the observation of magnetic-field (H)-induced ferroelectricity in PbCu₃TeO₇. We find that below T_N2 = 24 K, P_a is generated for transverse µ₀H_c > 8.3 T and longitudinal 16 T < µ₀H_a < 38 T, due to spin-flop (SF) transitions. We establish the phase diagram of PbCu₃TeO₇ for each H direction based on the electric and magnetic properties. Based on the exchange interactions obtained by the first-principles calculation, Monte Carlo (MC) simulations were performed to reveal spin configurations in each phase. Our calculations suggest that the P_a generated by µ₀H_c > 8.3 T and 16 T < µ₀H_a < 38 T stems from a cycloid spin phase rotating in the ab-plane.

Results

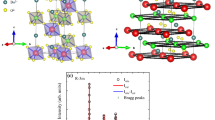
PbCu₃TeO₇ crystallizes in an orthorhombic structure (Pnma space group), in which Cu atoms form the two-dimensional kagome structure in the bc-plane (Fig. 1a, b). The kagome planes are buckled in a zigzag form to constitute the staircase kagome structure. The buckled kagome planes are also stacked along the a-direction and separated by Pb and Te atoms with a small interlayer distance of ~ 4 Å. The lattice parameters were obtained from the Rietveld refinement of powder XRD patterns; a = 10.484 Å, b = 6.347 Å, and c = 8.807 Å.³⁹ First-principles calculation based on the density functional theory (DFT) were performed to determine the values of the possible exchange interactions. Figure 1c summarizes the main intraplane exchange interactions labeled from J₁ to J₈ in the order of the distance between neighboring Cu pairs [Four additional interplane exchange interactions are not plotted here, but are summarized in Table 1].

Fig. 1

Crystal structure and magnetic susceptibility of PbCu₃TeO₇ single crystals. Crystal structures viewed along a the b-axis with all atoms and along b the a-direction showing the staircase kagome structure with spine Cu ions (green) and cross-tie Cu ions (blue). c Possible intralayer exchange interactions denoted from J1 to J8 in the order of the distance. d Temperature-dependent magnetic susceptibility data along each field direction

Table 1 Exchange parameters of PbCu₃TeO₇ determined by the DFT calculation. J_n (n = 1–8) refer to the intralayer exchange constants that appear in Fig. 1c, while J_in (n = 1–4) represent the interlayer ones

Figure 1d plots the magnetic susceptibility χ(Τ) data measured along each crystallographic direction. χ exhibits significant anisotropy consistent with the previous report by Koteswararao et al.³⁹ For H//a, there is an abrupt decrease of χ below T_N1 = ~ 36 K, signaling an AFM ordering, termed AFM 1. For H//c, χ starts to decrease below T_N2 = ~ 24 K and eventually becomes lower than the χ value measured along the a-axis, implying stabilization of another AFM ordering, termed AFM 2. However, for H//b, χ remains high without showing any anomaly. All these observations indicate that the crystallographic b-direction is the spin-hard axis in the two AFM phases, while the a-direction is the spin-easy axis in the AFM 1 phase. Moreover, with the stabilization of the AFM 2 phase, the crystallographic c-direction also becomes the spin-easy axis. Besides, a small kink is observed at ~ 17 K in the χ curve along H//a. It is also seen that the χ(Τ) curves along H//a and H//c cross each other at the anomaly at ~ 17 K.

Figure 2a–d present the electrical properties, i.e., the dielectric constant (ε_a), pyrocurrent I_p, and the corresponding electric polarization (P_a) curves. All are measured along the a-direction in the H//c configuration (H_c). In the low-field region (Fig. 2a), the ε_a curve exhibits a small kink in the vicinity of T_N2 = ~ 24 K. With increasing µ₀H_c, the kink feature grows and develops into a sharp peak; the peak intensity starts to increase above 6 T, shows an abrupt jump at µ₀H_c = 9 T, and becomes almost saturated for µ₀H_c ≥ 10 T (Fig. 2b). Finally, at the highest µ₀H_c = 14 T, ε_a exhibits the sharpest single peak. Consistent with this, we observe a dip feature in the I_p curves at µ₀H_c ≥ ~ 6 T (Fig. 2c). As the magnetic field increases beyond 8 T, the dip feature is progressively enhanced, exhibiting the most abrupt change between 8 and 9 T. Correspondingly, a finite P_a starts to appear at µ₀H_c ≥ 6 T and exhibits an abrupt increase between 8 and 9 T. The resultant P_a value at 2 K is summarized in Fig. 2e; it starts to appear at µ₀H_c ≥ 6 T, suddenly jumps between 8 and 9 T, and reaches the maximum value of 19.5 µC/m² at µ₀H_c = 14 T. The temperature, where P_a starts to appear, almost coincides with T_N2 = 24 K, implying that the AFM 2 phase at µ₀H_c ≥ 6 T is also ferroelectric. The sign of I_p is reversed after negative electric poling (−E_P) (not shown here), supporting the existence of ferroelectricity at µ₀H_c ≥ 6 T. In addition, for magnetic fields up to 14 T, the dip feature in I_p was only observed in this particular electric and magnetic field configuration, i.e., P//a and H//c.

Fig. 2

Temperature dependence of the electric and magnetic properties of PbCu₃TeO₇ for H//c. a, b Dielectric constant ε//a, c pyroelectric current, d electric polarization P//a, and f magnetization divided by H at selected H//c. e Electric polarization at various H//c estimated at 2 K

To further understand the spin configuration in the high-field region, the M/H curves are investigated along the c-axis in Fig. 2f at the bias fields µ₀H_c = 1, 7, 8, and 9 T. A sharp drop near T_N2 = ~ 24 K in the M/H curve at µ₀H_c = 1 T is consistent with the χ (H//c) curve in Fig. 1d, pointing to the stabilization of the AFM 2 phase. When the bias field is increased, the M/H curves remain nearly unchanged up to 6 T, then increase conspicuously between µ₀H_c = 8 and 9 T, and becomes almost temperature-independent at H_c = 9 T. This could result from an SF transition in the vicinity of µ₀H_c = 8 T. This observation is also consistent with the sharp increase of P_a between µ₀H_c = 8 and 9 T. Such concomitant sharp increases of P_a and M/H values imply that the SF phase of AFM 2 is responsible for the induced P_a at µ₀H_c ≥ 6 T.

In order to check possible H-induced P_a changes in other crystallographic directions and also at higher fields, we used a pulsed magnetic field up to 60 T to investigate the H-dependent ME current, magnetization (M), and ε curves in various H directions. Figure 3a summarizes the P(H) curve at 2 K for every H direction as obtained from the integration of the ME current. For H//c, P_a becomes finite at ~ 6 T and abruptly increases up to ~ 15 µC/m² at ~ 9 T; this is consistent with the P_a data obtained from the DC magnetic fields from the I_p measurement up to 14 T in Fig. 2. In this pulsed magnetic field experiment, we have verified that P_a remains almost constant up to 60 T. Moreover, we found in the H//a (H_a) measurement that P_a ~ 14 µC/m² also develops at µ₀H_a ≥ ~ 16 T and decreases again from µ₀H_a = 36 T to become zero at µ₀H_a = 41 T. Finally, we found no P_a for H//b.

Fig. 3

Magnetic-field dependence of the electric and magnetic properties of PbCu₃TeO₇ single crystals. a Electric polarization (P//a) and b magnetization M for each magnetic-field directions at 2 K. The arrows in the M curves indicate the potential SF transitions. ME coefficient (dP/dH), dielectric constant (ε//a), and field derivative of magnetization (dM/dH) at selected temperatures for c H//c and d H//a. For clarity, all the dP/dH, ε, and dM/dH curves above 2 K were shifted down by a vertical offset at each temperature

Figure 3b summarizes the corresponding magnetization M curve measured at 2 K obtained in pulsed magnetic fields up to 60 T. M increases linearly with H in the low-field region for each direction. M exhibits step-like increases at 8.3 T and 15.4 T for H//c and H//a, respectively. The linear extrapolations in both the M (H//c) curve at µ₀H_c > 8.3 T and the M (H//a) curve at µ₀H_a > 15.4 T result in a zero intercept at H = 0, implying that the spin ordering pattern realized at µ₀H_c > 8.3 T and µ₀H_a > 15.4 T in the high-field region is also AFM after the SF transition. In the configuration of H//a, an additional large step is observed at 38 T. The linearly extrapolated line along the M(H//a) curve at µ₀H_a > ~ 42 T still passed the zero offset, implying that another type of SF transition occurs. In contrast, for H//b, M increases linearly up to 60 T without any anomaly. Most importantly, in all the M vs. H curves presented in Fig. 3b, the fields where the SF transitions occur match those where the jumps in the P_a(H) curves are observed. This implies that the changes in the spin ordering pattern induced by the magnetic fields should be responsible for the P_a change. Furthermore, upon extrapolating the experimental magnetization data presented in Fig. 3b, we estimate the magnetic field for full saturation of magnetic moments to be ~ 120–140 T.

To determine the phase boundaries of the SF transitions as functions of the temperature and magnetic field, we investigated the field-derivative curves of P_a (dP_a/dH) and M (dM/dH), as summarized in Fig. 3c, d. For H//c (Fig. 3c), all the dP_a/dH, dM/dH, and ε_a curves exhibit a single sharp peak at the SF transition; their peak fields are consistent with each other and become almost temperature-independent. Moreover, the peaks are observed only below 24 K, proving that the SF transition occurs in the AFM 2 phase. The peak fields become higher at higher temperatures and eventually disappear at 24 K, which agrees with the temperature-dependent measurements shown in Fig. 2. The evolution of the peak fields can be clearly seen in Fig. 4a, in which the electric and magnetic phase diagram is presented for H_c.

Fig. 4

Temperature vs. magnetic-field phase diagram of PbCu₃TeO₇ for a H//c and b H//a. The data points indicate the anomalies in the dielectric constant (ε), magnetization (M), and electric polarization (P). Below the PM (paramagnetic), PE (paraelectric) phase, there exist several ordered phases: AFM 1, AFM 2, SF 1, SF 1’, SF 2, and FE (ferroelectric) phases

However, for H//a, both dP_a/dH and dM/dH curves display either peak or dip at µ₀H_a = ~ 16 T and ~ 38 T, pointing to the two consecutive SF transitions. The peak position at ~ 16 T in the dP_a/dH curve stays almost the same, while the second peak at ~ 38 T shifts to lower fields upon warming up to 22 K. Furthermore, both peaks disappear above 24 K. The corresponding dM/dH curves exhibit a peak and a dip feature at almost same temperatures where the peaks in dP_a/dH are observed. The peak and dip feature also disappears above 24 K. This directly proves that these field-induced SF transitions occur only within the AFM 2 phase stabilized below 24 K. The evolution of the peak or dip locations in dM/dH is also summarized in the phase diagram of Fig. 4b.

Based on the data presented in Figs. 2 and 3, we plot the phase diagram of PbCu₃TeO₇ for H//c and H//a in Fig. 4a, b, respectively. The peak positions in dP_a/dH, dM/dH, ε_a(H), ε_a(T), χ(H), and χ(T) and the temperatures, at which P_a(T) starts to appear or disappear, are drawn. The phase boundaries from each measurement are consistent, displaying three major phases: a high-temperature paramagnetic paraelectric phase, the AFM 1 below T_N1 = 36 K, and AFM 2 below T_N2 = 24 K. In particular, we find evidence of finite electric polarization and ferroelectricity for H//c above 6 T with a concomitant, sharp SF transition. Thus, we represent the ferroelectric phase realized for H//c above 6 T as SF 1 and FE. Moreover, for H//a, we find two SF-like transitions inside the AFM 2 phase, and the resulting phases are termed SF 1’ and SF 2. In particular, in the SF 1’ region, we observe the ferroelectric polarization along the a-axis, as summarized in Fig. 4b.

In order to understand the possible magnetic structures in each phase and the H-induced electric polarization, we conducted classical MC simulations using the exchange constants, which were determined by the DFT calculation as described in the Methods section and are summarized in Table 1. The studied compound contains magnetic ions with lowest possible spin (S = 1/2) and, therefore, a variant of quantum MC simulations possibly would have been better suited to study its magnetic properties. However, we use here classical MC calculations to obtain a qualitative picture and use the results such as modulation wave vectors as inputs for the symmetry analysis of ME interactions described below. The results of MC simulations supported by the symmetry analysis are in good agreement with the experimental findings. The model Heisenberg Hamiltonian has the form,

$${\cal H} = \mathop {\sum }\nolimits_{ < ij > } J_{ij}\vec S_i \cdot \vec S_j + \mathop {\sum }\nolimits_i \left( {K_xS_{ix}^2 + K_yS_{iy}^2 + K_zS_{iz}^2} \right) - \mathop {\sum }\nolimits_i \vec H \cdot \vec S_i,$$

(1)

where the spins $\vec S_i$ are classical vectors of unit length, $\vec H$ is the magnetic field, K_α (α = x,y,z) are anisotropy constants, and we assume that the axes x, y, and z are along the a-, b-, and c-directions, respectively. According to the succession of anomalies in the χ (T) data, one can conclude that K_x < K_z < K_y. We find that the simulation results based on the values K_x = −1 meV, K_y = 0.05 meV, and K_z = 0 could provide qualitative correspondence with the experiments. Preliminary simulations of 20 × 20 × 20 unit cells (96,000 magnetic ions) first identified that the magnetic structure is modulated along the b-direction with a wave vector close to $\vec k = \left( {0,\frac{1}{3},0} \right)$. Therefore, subsequent studies were performed using the 4 × 75 × 4 simulation box.

In order to understand the magnetic structure and its coupling to the electric polarization, we performed a symmetry analysis. In the $\vec k = \left( {0,\frac{1}{3},0} \right)$ point of the Brillouin-zone, the Pnma space group has four two-dimensional irreducible representations (IRs) Δ_i (i = 1,2,3,4). The magnetic structure belongs to the Δ₂⊗V′ exchange multiplet (here V′ is the pseudo-vector representation).⁴² This multiplet splits into the direct sum of IRs Δ₄, Δ₁, and Δ₃, according to which the x, y, and z components of spins transform, respectively, and we denote the respective order parameters by (a₁,a₂), (b₁,b₂), and (c₁,c₂).

The appearance of the modulated magnetic structure is in accordance with macroscopic symmetry since it allows the Lifshitz invariants

$$a_1\frac{{a_2}}{{\partial y}} - a_2\frac{{a_1}}{{\partial y}},\qquad b_1\frac{{b_2}}{{\partial y}} - b_2\frac{{b_1}}{{\partial y}},\qquad c_1\frac{{c_2}}{{\partial y}} - c_2\frac{{c_1}}{{\partial y}},$$

(2)

which result in the modulation of magnetic order along the b-axis.

According to the MC simulations at a zero magnetic field, upon lowering the temperature, the first phase transition occurs at T^MC_N1 = 35 K and shows a spatially modulated order parameter (a₁,a₂). Further cooling results in the additional appearance of a spatially modulated (c₁,c₂) at T^MC_N2 = 28 K. Thus, the AFM 1 phase is sinusoidally modulated, whereas in the AFM 2 phase, spins lie in the ac-plane, forming a proper screw-type spin order. In the AFM 2 phase, the spin modulation period is approximately 25 unit cells along b. In spin-ordered phases AFM 1 and AFM 2, the spatially varying order parameters can be approximated with good accuracy by harmonic functions, e.g., a₁ = A Cos(k y+y₀) and a₂ = A sin(k y + y₀). Therefore, in the following, we define amplitudes A, B, and C of the order parameters. The temperature dependence of amplitudes A and C is shown in Fig. 5a, whereas an example of a spatially modulated order parameter is presented in Fig. 5b.

Fig. 5

Results of the MC simulation on PbCu₃TeO₇. a Temperature dependence of order parameter amplitudes A and C at a zero-applied magnetic field, b spatial variation of the order parameters (a1, a2) along the b-direction, and c the magnetization, d polarization, and e, f order parameters as functions of the magnetic field along various directions

The dependence of the magnetization on external H applied along various directions is shown in Fig. 5c. Upon application of H_c above ≈ 1.2 A.U., the plane of spin rotations changes into the ab-plane and becomes perpendicular to the magnetic field as shown in Fig. 5e. This cycloidal spin structure is described by spatially modulated (a₁,a₂) and (b₁,b₂) and possesses electric polarization along a due to the ME interaction

$$\left( {a_1b_1 + a_2b_2} \right)P_a,$$

(3)

in accordance with the experimental results for the SF 1 phase.

However, the application of H_a results in a more complex behavior. The symmetry allows the interaction

$$\left( {a_1b_1c_2 + a_1b_2c_1 + a_2b_1c_1 - a_2b_2c_2} \right)M_a,$$

(4)

where M_a is the macroscopic magnetization along the a-axis. According to interaction (4), in the presence of the order parameters (a₁,a₂) and (c₁,c₂), the application of H_a induces a spatially varying order parameter that is modulated with a wave vector twice that of (a₁,a₂) and (c₁,c₂) and which we denote by $\left( {b_1^\prime ,b_2^\prime } \right)$ to distinguish it from (b₁,b₂) modulated with the same k. The order parameters (b₁,b₂) and $\left( {b_1^\prime ,b_2^\prime } \right)$ have the same symmetry; however, according to the results of the MC calculations, the latter describes the magnetic moment components along the c-axis and is given by

$$b_1^\prime \sim \left( {a_1c_2 + a_2c_1} \right)M_a,$$

(5)

$$b_2^\prime \sim \left( {a_1c_1 - a_2c_2} \right)M_a,$$

(6)

thus being proportional to H_a. Here, we have $b_1^\prime = B^\prime {\mathrm{cos}}\left( {2k\,{y} + {y}_0} \right)$ and $b_2^\prime = B^\prime {\mathrm{sin}}\left( {2k\,{y} + {y}_0} \right)$. The field dependences of A, B, $B^\prime$, and C are shown in Fig. 5f. Due to the fact that $\left( {b_1^\prime ,b_2^\prime } \right)$ is modulated with a doubled wave vector, its appearance with the application of H_a does not result in the emergence of electric polarization because the ME interaction represented by Eq. 3 averages to zero after the integration over the volume of the crystal. Therefore, model Hamiltonian (1) alone cannot explain the observation of P_a in the SF 1 phase realized under intermediated H_a.

However, our MC simulations show that further increases in H_a above ≈ 5.3 A.U. eventually results in an SF transition, at which the plane of rotation changes to the bc-plane, as shown in Fig. 5f, being consistent with the experiments identifying the SF 2 phase. At intermediate H_a < 5.3 A.U., it is possible to observe another field-induced phase transition, which can result either in a phase with all order parameters (a₁,a₂), $\left( {b_1^\prime ,b_2^\prime } \right)$, and (c₁,c₂) being commensurate and non-zero or in an incommensurate phase with order parameters (a₁,a₂) and $\left( {b_1^\prime ,b_2^\prime } \right)$ modulated with the wave vector $\vec k$ and (c₁,c₂) with $2\vec k$. Both possible phases will result in the emergence of P_a owing to Eq. 3. Such a field-induced phase transition can result from more complex magnetic anisotropies present in PbCu₃TeO₇, which are not captured in our simplified Hamiltonian. Thus, it represents a transition to a phase intermediate between the zero-field, ac proper screw, and high-field, bc cycloidal structures. Neutron diffraction studies are required in order to clarify the spin structure of this intermediate field-induced phase.

All of the spin structures obtained by the MC simulations are summarized in Fig. 6. In the ferroelectric phase, the spin structure is cycloidal and the spontaneous P emerges along the a-axis. The microscopic origin of P_a can be revealed by rewriting Eq. 3 in terms of spins. The corresponding analysis shows that P_a arises due to contributions from both single-spin, described, e.g., by p-d hybridization model, and two-spin interactions, possessing vector spin products. The latter can be interpreted as IDM²² or spin current²⁴ models. In the spin current model, the local electric polarization is expressed by

$${\boldsymbol{P}}_{{\boldsymbol{ij}}} \propto {\boldsymbol{e}}_{ij} \times \left( {{\boldsymbol{S}}_i \times {\boldsymbol{S}}_j} \right),$$

(7)

where e_ij is the propagation vector between S_i and S_j. In PbCu₃TeO₇, e_ij is along the b-direction and the spin current j_s( = S_i × S_j) is along the c-direction. Thus, the spin current model predicts the direction of P_ij ( = e_ij × j_s) to be along the a-axis, consistent with the experimental results. In addition, the polarizations P_ij between each of the two spins have the same direction in the cycloidal order, which thus results in the macroscopic electric polarization P_a.

Fig. 6

Schematics of spin arrangements in the a AFM 1, b AFM 2, c SF 1’, and d SF 1 and SF 2 phases in PbCu₃TeO₇. All the spin components were drawn based on the results of the MC simulations

In the SF 2 phase realized under H//a higher than 38 T, the spin rotation plane flips to the bc-plane. However, as the magnetic field is high, spins do not lie only in the bc–plane, but also are canted to the a-direction, resulting in the field-induced transverse conical (TC) spin order. In principle, the TC spin order should give rise to electric polarization P along the c-direction according to the spin current model. Macroscopic symmetry also allows a form of the ME interaction

$$\left( {b_1c_2 - b_2c_1} \right)P_c$$

(8)

The MC simulations show that at H_a > 5.3 A.U., the modulated order parameters (b₁,b₂) and (c₁,c₂) develop in a way that homogenous P_c arises owing to Eq. 8. Thus, this TC phase is ferroelectric with the polarization along the c-direction. In the experiments, however, we have not confirmed P//c yet as the pulsed field experiments have been so far performed only at the P//a configuration.

Discussion

The geometric spin frustration inherent to the kagome lattice generically suppresses the static long-range spin order. Therefore, ME/multiferroic properties, which are mostly coupled to a specific spin ordering, are rare in the kagome structure. However, the “distorted” kagome structures including the kagome staircase can relieve the degree of spin frustration either by anisotropic distortion in the kagome intralayer or by developing an interlayer interaction. As a result, several multiferroic/magnetoelectric compounds with the “distorted” kagome structures is characterized by only moderate spin frustration; for example, the ratio between the Curie–Weiss temperature and the Neel temperature θ_CW/T_N is ~ 2 in KCu₃As₂O₇(OD)₃, ~ 3.3 in Ni₃V₂O₈, and ~ 4 in PbCu₃TeO₇. More importantly, such “distorted” kagome materials possess significant competing next-nearest interaction, which can often produce noncollinear spin orderings that are directly linked to their ferroelectric and ME properties. Therefore, significant exchange interactions beyond the first neighbors and the lifted geometric spin frustration should be regarded as common key features relevant for both Ni₃V₂O₈ and the presently studied PbCu₃TeO₇.

In recently reported multiferroic KCu₃As₂O₇(OD)₃^37,38 with monoclinic two-dimensional kagome planes, the anisotropic intralayer distortion plays a dominant role in stabilizing a noncollinear spin ordering; it has nearly perfect two-dimensional kagome planes with the ratio of intralayer to interlayer interaction J_inter/J_intra ~ 0.01.³⁷ However, its intralayer distortion is significant enough to give rise to a high ratio of the intralayer lattice constants a/b of ~ 1.72, thus relieving the geometric frustration in the kagome plane considerably and resulting in a long-range magnetic ordering below 7 K.

However, kagome staircase compound PbCu₃TeO₇ studied here exhibits a much higher J_inter/J_intra ~ 1 (Table 1), thereby more strongly mitigating spin frustration through the interlayer coupling. Owing to the inherent characteristic of the kagome staircase structure, the ratio of the intralayer lattice constants c/b of ~ 1.4 in PbCu₃TeO₇ is still high enough to cause further reduction in the degree of spin frustration. The situation for kagome staircase compound Ni₃V₂O₈ is similar; J_inter/J_intra ~ 0.4⁹ and the ratio of the intralayer lattice constants is ~ 1.39¹³. Therefore, both PbCu₃TeO₇ and Ni₃V₂O₈ have a high number of considerable magnetic exchange interactions, which act together to reduce the geometric spin frustration and result in long-range incommensurately modulated magnetic ordering. External magnetic field perturbs the three-dimensional magnetic interactions in these staircase kagome compounds, which results in complex phase diagrams together with rich anisotropic behavior, as found in PbCu₃TeO₇ as well as in Ni₃V₂O₈.

The phase diagram of PbCu₃TeO₇ can be compared with that of Ni₃V₂O₈, where S = 1 and a cycloidal spin ordering is stabilized between 4 and 6.3 K in the low-temperature insulating phase. As another staircase kagome compound with S = 1/2, PbCu₃TeO₇ similarly exhibits a kind of noncollinear spin ordering, i.e., a proper screw-type spin ordering, below T_N2 = 24 K at a zero magnetic field. Both staircase compounds also form a collinear sinusoidal spin ordering at high temperatures above their noncollinear spin orderings. In this sense, they share close similarities in the spin ordering patterns. Furthermore, both compounds share another similarity of displaying complex electric/magnetic phase diagrams that are considerably different for each H direction.

However, Ni₃V₂O₈ has additional magnetic anisotropy, so that its spin rotation planes contain the spin propagation direction parallel to the Ni spins, forming a cycloid spin structure. Moreover, it exhibits two kinds of canted AFM order below 4 K, whereas PbCu₃TeO₇ maintains a proper screw-type spin ordering below T_N2, whose spin rotation plane is perpendicular to the spin propagation direction parallel to Cu spines. Therefore, in PbCu₃TeO₇, the magnetic field is used to control effective magnetic anisotropy to further induce SF transitions and resultant spin cycloid phases with ferroelectric polarization. This fundamental difference in their magnetic anisotropy may stem from the fact that Ni₃V₂O₈ possesses a larger spin value (S = 1) than PbCu₃TeO₇ (S = 1/2), thereby exhibiting additional sources of magnetic anisotropy due to zero-field splitting and stronger spin–orbit interactions. This may also explain why the polarization is larger in Ni₃V₂O₈ (~60 µC/m²)¹⁴ than PbCu₃TeO₇ (~15 µC/m²) and why the resultant field vs. temperature phase diagram of Ni₃V₂O₈ looks more complex than that of PbCu₃TeO₇.

Finally, we re-emphasize that the kagome staircase structure with both intralayer distortion and interlayer competing interaction can be a useful platform for searching for new field-induced ferroelectric polarization. In particular, the delicate balance in the magnetic anisotropy in three-dimensionally interacting spin networks can produce rich phase evolutions with various spin structures per different magnetic field directions. Therefore, our observation of field direction-dependent multiferroicity and nontrivial spin patterns in PbCu₃TeO₇, combined with former studies on Ni₃V₂O₈, points to an opportunity that ample field-induced phases and ME/multiferroic effects can also be found in other staircase kagome structures.

In conclusion, we have investigated the ME properties in new staircase kagome magnet PbCu₃TeO₇ with S = 1/2 Cu²⁺ spins. The investigation of electric and magnetic properties has revealed that PbCu₃TeO₇ becomes ferroelectric, exhibiting P_a at µ₀H_c > 8.3 T and 15 T < µ₀H_a < 38 T and its field-induced phase transitions are concomitant with the SF transitions. By means of MC calculations, we establish a model of spin structures for each phase that mostly explains the origin of magnetic-field-induced P. Our investigation reveals that staircase kagome magnet PbCu₃TeO₇ based on S = 1/2 (Cu²⁺) is a fertile source of competing interactions that create ferroelectric polarization owing to the realization of various inhomogeneous spin textures induced by magnetic fields. Further studies of neutron scattering and X-ray diffraction under a high-magnetic field will be helpful to fully identify the spin structures and to understand the origin of ME coupling in each high-field phase.

Methods

Single crystals of PbCu₃TeO₇ were grown using the flux method. First, a PbCu₃TeO₇ polycrystalline sample was prepared by the solid-state reaction method using starting materials PbO, CuO, and Te. They were ground with a molar ratio of 1: 3: 1 and synthesized at 750 °C for 5 days with three intermediate grindings. In order to grow single crystals, the polycrystalline of PbCu₃TeO₇ and NaCl/KCl flux was mixed with a molar ratio of PbCu₃TeO₇: NaCl: KCl equal to 1: 10: 10. The mixture was heated at 800 °C for 24 h and then cooled to 650 °C at a rate of 1 °C/h. The single crystals were extracted by washing with hot water.

For the electric measurements, we shaped the single crystal into thin plates, whose surface was normal to the crystal a-axis. The shaped crystal size was quite small with an area of 0.13 mm² and a thickness of 140 µm. The electrodes on both sides of the plate were formed with silver epoxy. We measured the pyroelectric and ME current (∝dP/dt) using KE617 electrometer and the dielectric constant using AH2550A capacitance bridge at a frequency of 1 kHz. The magnetic properties were collected using a vibrating sample magnetometer (VSM). These measurements were done in the 9 T PPMS^TM (Quantum Design) and the 14 T Cryogenic^LTD magnet system in the temperature (T) range from 2 K to 50 K.

The high-magnetic field ME current and magnetization measurements, using SR 570 current amplifier and the induction magnetometry technique, respectively, were done in the pulsed magnetic field up to 60 T at the NHMFL pulsed-field facility at LANL. The magnetization values from the pulsed field were calibrated using the VSM data measured in the 9 T PPMS^TM.

The DFT calculations of the exchange constants in PbCu₃TeO₇ were performed using the Vienna Ab initio Simulation Package.⁴³ We used the GGA+U approach with the on-site repulsion for Cu atoms by the Dudarev method.⁴⁴ The value U_eff = U−J = 10 eV was chosen similar to other DFT studies of Cu-containing magneloelectrics.^45,46 The plane-wave cutoff energy of 500 eV was used, whereas the Brillouin-zone was integrated with the 4 × 6 × 4 mesh determined by the Monkhorst–Pack scheme.⁴⁷ In the previous work,³⁹ the most important exchange paths were studied identifying eight (J₁ to J₈) intra and four (J_i1 to J_i4) interkagome plane couplings. In the present work, we calculate the respective exchange constants, which are summarized in Table 1.