Multidimensional Bose quantum error correction based on neural network decoder

Abstract

Boson quantum error correction is an important means to realize quantum error correction information processing. In this paper, we consider the connection of a single-mode Gottesman-Kitaev-Preskill (GKP) code with a two-dimensional (2D) surface (surface-GKP code) on a triangular quadrilateral lattice. On the one hand, we use a Steane-type scheme with maximum likelihood estimation for surface-GKP code error correction. On the other hand, the minimum-weight perfect matching (MWPM) algorithm is used to decode surface-GKP codes. In the case where only the data GKP qubits are noisy, the threshold reaches σ ≈ 0.5 ($\bar{p}\approx 12.3 \%$). If the measurement is also noisy, the threshold is reached σ ≈ 0.25 ($\bar{p}\approx 10.02 \%$). More importantly, we introduce a neural network decoder. When the measurements in GKP error correction are noise-free, the threshold reaches σ ≈ 0.78 ($\bar{p}\approx 15.12 \%$). The threshold reaches σ ≈ 0.34 ($\bar{p}\approx 11.37 \%$) when all measurements are noisy. Through the above optimization method, multi-party quantum error correction will achieve a better guarantee effect in fault-tolerant quantum computing.

Introduction

Reliable execution of large-scale quantum computing requires quantum error correction. The method of redundant information is an important method to store qubit information in continuous variable system or boson model^1,2, combined with classical error correction³. Numerous experimental platforms are now available to implement error correction operations for physical qubits encoding logical qubits. However, with the expansion of hardware overhead and the advancement of quantum bits in quantum systems⁴, it brings great challenges to quantum error correction. Intriguingly, boson quantum error correction has emerged as an efficient infinite-dimensional quantum error correction, where logical qubits encoded by numerous physical qubits are encoded in a system of continuous variables, or the boson model. It provides an infinite dimension for the encoding of quantum information under Hilbert space⁵. The most representative single boson model mainly includes boson error correction codes such as cat code⁶, binomial code⁷, and Gottesman-Kitaev-Preskill (GKP) code⁸.

At present, GKP codes have achieved great value in suppressing the logic error rate to be arbitrarily small under a single model, which has attracted extensive attention of boson error correction⁹. But there is a shortage, GKP code can not correct the offset error to the phenomenon space larger than the critical value in the continuous variable system. In reference to previous research¹⁰, the influence of noise is gradually weakened by using multi-qubit control gates to achieve higher-precision fault tolerance thresholds. In addition, research also shows that¹¹, quantum computation of holographic codes is realized by non-adiabatic multi-bit quantum gates and more good fidelity performance. Recently, some experts have also proposed that the combination of GKP code and color code can solve the error problem of non-horizontal gates¹² in the information transmission process, which is good for fault-tolerant calculations. Due to the topology and rotatability of surface codes, considering the combination of surface codes with GKP codes, the continuous error information that can be collected during the error correction process of GKP codes can improve the performance of next-level concatenated error correction. We know that the topological surface code itself has a stabilizer, and the threshold can reach about 0.34 in error correction and fault tolerance, but the additional error information measured by the stabilizer of the GKP code is introduced into the surface code, and the threshold can be increased to about 0.78. The error correction scheme of Surface-GKP code is similar to GKP, and can usually use Steane type scheme^13,14, Knill Glancy type scheme^15,16, and teleportation-based scheme¹⁷. The error correction scheme of the Steane type scheme is relatively simple to implement in the hardware circuit and is widely used. In order to make up for the deviation of the traditional Steane-type scheme in error correction, it cannot provide the best correction scheme. In the article¹⁸, the error offsets u₁ and u₂ of the data qubit and auxiliary qubit are assumed to be equal, where u represents the error bias caused by $\hat{p}$ and $\hat{q}$ in the polarizer. The Steane-type error correction scheme, which guarantees the maximum likelihood estimation through the above operations, provides higher performance. In order to ensure the normal error correction of the Steane-type scheme under the extremely low confidence interval, we have made a moderate modification in the offset error correction and changed the variance estimation to the standard deviation.

In the surface-GKP decoding process, we first select a simple decoding algorithm based on the Minimum Weight Perfect Matching (MWPM)¹⁹ algorithm to apply to the 3D spatiotemporal graph, and thresholds range from σ ≈ 0.25 ($\bar{p}\approx 10.02 \%$) to σ ≈ 0.5 ($\bar{p}\approx 12.5 \%$) in the perfect test of GKP decoding. The MWPM decoder threshold reaches $\bar{p}\approx 12.3 \%$ when the data qubit and stabilizer measurements are noisy but the GKP error correction is perfect, and σ ≈ 0.25 when the GKP error correction is also noisy. These results show that the surface-GKP code is comparable to the toric-GKP code under the same noise model. The neural network decoder is fast enough to decode in topological quantum error correction codes²⁰. It achieves an exponential improvement, and solves the hardware overhead²¹ problem by using the algorithmic improvement. In order to improve the decoding effect of the surface-GKP code, we introduce the currently popular neural network decoder, which uses the convolution operation of the neural network to decode the surface-GKP code under the continuous variable system, with a threshold of σ ≈ 0.78 ($\bar{p}\approx 15.12 \%$). Compared with the decoding of the surface code alone, the combined error correction code increases the decoding threshold to about 15%, which provides a higher limit guarantee for quantum error correction calculation.

Result

GKP code

GKP codes encode a qubit into a harmonic oscillator²², and we define the position and momentum operators as: $\hat{q}=({\hat{a}}^{{\dagger} }+\hat{a})/\sqrt{2}$ and $\hat{p}=i({\hat{a}}^{{\dagger} }-\hat{a})/\sqrt{2}$ where $\hat{a}$ and ${\hat{a}}^{{\dagger} }$ are annihilation and creation operators satisfying $[\hat{a},{\hat{a}}^{{\dagger} }]=1$. We compose the code space of GKP qubits by two commutable stabilizer operators as follows:

$${\hat{S}}_{p}={e}^{-i2\sqrt{\pi }\hat{p}},\quad {\hat{S}}_{q}={e}^{i2\sqrt{\pi }\hat{q}}.$$

(1)

When $| {\xi }_{q}| ,| {\xi }_{p}|\, < \,\sqrt{\pi }/2$ without the influence of noise, the phase space shift error of the ideal GKP qubit $\exp [i({\xi }_{p}\hat{q}-{\xi }_{q}\hat{p})]$ can be detected and corrected. Next, the logical Pauli operators X and Z are defined as:

$$\bar{X}={e}^{-i\sqrt{\pi }\hat{p}},\quad \bar{Z}={e}^{i\sqrt{\pi }\hat{q}}.$$

(2)

We clearly find that there are ${\bar{X}}^{2}=\hat{{S}_{q}}$ and ${\bar{Z}}^{2}=\hat{{S}_{p}}$, which proves that $\bar{X}$ (or $\bar{Z}$) commutes with $\hat{{S}_{p}}$ and $\hat{{S}_{q}}$. The logic state in the noise-free case is rewritten as:

$$\begin{array}{l}\left\vert \bar{0}\right\rangle \propto \mathop{\sum}\limits_{n\in {\mathbb{Z}}}\delta (q-2n\sqrt{\pi })\left\vert q\right\rangle =\mathop{\sum}\limits_{n\in {\mathbb{Z}}}\left\vert q=2n\sqrt{\pi }\right\rangle ,\\ \left\vert \bar{1}\right\rangle \propto \mathop{\sum}\limits_{n\in {\mathbb{Z}}}\delta (q-(2n+1)\sqrt{\pi })\left\vert q\right\rangle =\mathop{\sum}\limits_{n\in {\mathbb{Z}}}\left\vert q=(2n+1)\sqrt{\pi }\right\rangle .\end{array}$$

(3)

Quantum error correction requires the help of quantum circuits²³, among which Clifford gates are the most representative. On GKP qubits, the Clifford operator²⁴ can be implemented using Gaussian operations. The specific Clifford group set is as follows:

$$\begin{array}{lll}{\hat{S}}_{{{{\rm{gkp}}}}}&=&\exp \left[i\frac{{\hat{q}}^{2}}{2}\right],\\ {\hat{H}}_{{{{\rm{gkp}}}}}&=&\exp \left[i\frac{\pi }{2}{\hat{a}}^{{\dagger} }\hat{a}\right],\\ {{{{\rm{CNOT}}}}}_{{{{\rm{gkp}}}}}^{j\to k}&=&{{{{\rm{SUM}}}}}_{j\to k}\equiv \exp \left[-i{\hat{q}}_{j}{\hat{p}}_{k}\right].\end{array}$$

(4)

Pauli X and Z in (3) are ideal, but they are not normalizable and require infinite energy to squeeze. In noisy ambient states, we need to introduce finitely squeezed Gaussian states weighted by a Gaussian envelope. Instead of δ function, the GKP state in this noisy environment becomes:

$$\begin{array}{l}\left\vert \tilde{0}\right\rangle \propto \mathop{\sum}\limits_{n\in {\mathbb{Z}}}\int\nolimits_{-\infty }^{\infty }{e}^{-\frac{{\Delta }^{2}}{2}{(2n)}^{2}\pi }{e}^{-\frac{1}{2{\Delta }^{2}}{(q-2n\sqrt{\pi })}^{2}}\left\vert q\right\rangle dq,\\ \left\vert \tilde{1}\right\rangle \propto \mathop{\sum}\limits_{n\in {\mathbb{Z}}}\int\nolimits_{-\infty }^{\infty }{e}^{-\frac{{\Delta }^{2}}{2}{(2n+1)}^{2}\pi }{e}^{-\frac{1}{2{\Delta }^{2}}{(q-(2n+1)\sqrt{\pi })}^{2}}\left\vert q\right\rangle dq,\end{array}$$

(5)

where Δ represents the width of each peak in the Wigner function of the true GKP state. For a unified representation, the GKP state under arbitrary noise $\left\vert \tilde{\psi }\right\rangle =\alpha \left\vert \tilde{0}\right\rangle +\beta \left\vert \tilde{1}\right\rangle$ can be defined as the GKP state in the noiseless state $\left\vert \bar{\psi }\right\rangle$ Gaussian distribution affected by shift error:

$$\left\vert \tilde{\psi }\right\rangle \propto \iint {e}^{-\frac{{u}^{2}+{v}^{2}}{2{\Delta }^{2}}}{e}^{-iu\hat{p}}{e}^{iv\hat{q}}\left\vert \bar{\psi }\right\rangle dudv.$$

(6)

Using the Pauli rotation approximation theorem from the Gaussian displacement error channel ${{{\mathcal{N}}}}$, these errors can be applied to the noise-free GKP state in the variance σ² as:

$${{{\mathcal{N}}}}(\rho )\equiv \iint {P}_{\sigma }(u){P}_{\sigma }(v){e}^{-iu\hat{p}}{e}^{iv\hat{q}}\rho {e}^{-iv\hat{q}}{e}^{iu\hat{p}}dudv,$$

(7)

where ${P}_{\sigma }(x)=\frac{1}{\sqrt{2\pi {\sigma }^{2}}}{e}^{-\frac{{x}^{2}}{2{\sigma }^{2}}}$ is Gaussian distribution function with variance σ².

Under this error channel²⁵, the coherent displacement error is replaced by the displacement error of the incoherent mixed state in Fig. 1, due to the use of the Pauli rotation approximation theorem. In the case of incoherent misplaced mixed states, we can simplify the analysis to distinguish between pure and mixed states by measuring $\hat{q}$ or $\hat{p}$, but the disadvantage is that it increases the noise intensity compared with the coherent displacement error, and the number of photons in GKP also increased. Here we introduce a novel Steane error correction scheme to correct small Gaussian shift errors in the $\hat{q}$ or $\hat{p}$ quartic models caused by incoherent mixed states. Novel Steane error-corrected quantum circuit consisting of CNOT gates, homodyne measurements, and ideal GKP auxiliary qubits. To characterize the completeness of the circuit, we consider the inverse CNOT gate, which is shown in Section III to demonstrate the complete new Steane error correction process.

Fig. 1: Schematic diagram of GKP states with five photon numbers.

a The left image is the calculated ground state $\left\vert {0}_{{{{\rm{gkp}}}}}\right\rangle$ with an approximate GKP quantum state with an average photon number $\bar{n}=5$. b The right image is a GKP quantum state with an average photon number computational ground state $\left\vert {1}_{{{{\rm{gkp}}}}}\right\rangle$ of the approximate GKP quantum state of $\bar{n}=5$.

Surface code

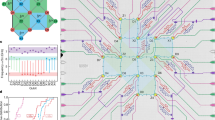
The surface code is a plane mapping of the toric code^26,27, and it is also a good stabilizer code due to its topology. The surface code is defined on a 2D square lattice, auxiliary qubits^28,29 can be attached to the qubits we want to protect, and the measurement of syndromes can be performed, and the intersection of syndromes can help identify the most likely error operators. For the chosen lattice, the qubits are clearly indicated in Fig. 2(a). As shown in Fig. 2(b), the four internally adjacent vertices form two types of lattice operators X and Z, and the boundary is formed by two vertices. As shown in Fig. 2(c), the lattice stabilizer associated with qubits 1, 2, 6, and 7 denoted by X, will be X₁X₂X₆X₇. On the other hand, the lattice stabilizer associated with qubits 8, 9, 13, and 14 represented by Z would be Z₈Z₉Z₁₃Z₁₄. To simplify the representation, we can use yellow for all stabilizer generators containing X, and blue for all stabilizer generators containing Z. If we denote the set of all yellow (blue) patches by {B_p}({W_p}), we can define a stabilizer on lattice p as follows:

$${B}_{p}=\mathop{\prod}\limits_{i\in v}{\sigma }_{i}^{x},{W}_{p}=\mathop{\prod}\limits_{i\in p}{\sigma }_{i}^{z}.$$

(8)

Fig. 2: Schematic diagram of a surface code with a code distance of 5.

a The data qubit corresponds to the vertex of the lattice. b Qubits form two types of lattice operators: X and Z. c The four data quantum bits surrounding the X(Z) ancilla qubits form an X(Z) stabilizer. d The surface code has periodic boundaries, and the logical operators can also be on both sides of the lattice.

For surface codes, logical operators operate on both sides of the lattice, as shown in Fig. 2(d), and can be expressed as Z = Z₁Z₂Z₃Z₄Z₅; X = X₅X₁₀X₁₅X₂₀X₂₅. Obviously, logical operators span two boundaries of the same type. The codeword length³⁰ is determined as the product of the side lengths, expressed in the number of qubits, and for the surface code in Figure, we have N = L_X ⋅ L_Z = 5 ⋅ 5 = 25.

The surface-GKP code

In order to solve the situation that the GKP code is difficult to correct the phase offset exceeding $\sqrt{\pi }/2$ in the single-mode space, the logical error rate in the GKP code space cannot be suppressed to an arbitrarily low level. Therefore, we connect GKP codes with topological surface codes³¹, namely surface-GKP codes, for quantum gates and quantum computation under noise reduction.

In the combination of the two, each data qubit in the surface code is replaced by a single-mode GKP code³². The advantage of this is that it provides the protection of the stabilizer, that is, the GKP single-mode measurement K times stabilizer ${\hat{S}}_{q}^{(k)}$ and ${\hat{S}}_{p}^{(k)}$. Secondly, additional auxiliary qubits can be GKP encoded, and the underlying noise model can be checked by measuring auxiliary qubits, which can be used to accurately estimate and correct noise on each GKP data pattern. In mathematical statistics, the qubits of the surface-GKP code are consistent with the number of qubits of the surface code, that is, d² data qubits and d² − 1 syndrome qubits to get a distance-d code.

$${\hat{S}}_{q}^{(k)}\equiv \exp [i2\sqrt{\pi }{\hat{q}}_{k}],\quad {\hat{S}}_{p}^{(k)}\equiv \exp [-i2\sqrt{\pi }{\hat{p}}_{k}].$$

(9)

Among them, k is the code distance: k ∈ {1, ... , d²}. Since the surface code has 1/2 degree of freedom³³, that is, the probability of error occurring in X is equal to the probability of error occurring in Z, corresponding to the parity check operator. There are two types: all X stabilizers can check for Z errors, and all Z stabilizers can check for X errors. In order to reduce the displacement error caused by the rotation code, we can modify the check operator of the surface code as shown in Fig. 3.

Fig. 3: Schematic diagram of surface-GKP code with a code distance of 5.

The small white circles in the surface-GKP code with code distance d = 5 represent the data GKP qubits, and the small gray circles correspond to each data GKP qubit one-to-one, which is used to measure the auxiliary GKP quantum of the stabilizer of the data GKP qubit bits. The small dark green circles and the small dark blue circles represent the syndrome qubits of the surface-GKP code, which are used to measure the Z type and X type surface code stabilizers of the data GKP qubit, respectively. The data GKP qubits and auxiliary bits corresponding to the light yellow and light blue squares and the corresponding SUM gates and inverse gates constitute the stabilizer generator.

Each $\bar{X}$-type parity check involves two $\bar{X}$ and two ${\bar{X}}^{{\dagger} }$, while each $\bar{Z}$-type parity check³⁴ only involves $\bar{Z}$. (Note in contrast to regular discrete qubits we do not have $\bar{X}={\bar{X}}^{{\dagger} }$ and $\bar{Z}={\bar{Z}}^{{\dagger} }$ outside the GKP codespace). In the process of parity checking, the circuit shown in Fig. 4 is used. Each GKP auxiliary qubit ($\bar{X}or\bar{Z}$) interacts with the adjacent four data qubits, and the Z operators which check is ${\bar{C}}_{Z}={e}^{i\hat{Q}\otimes \hat{Q}}$, and the X operator is a mixed check ${\bar{C}}_{X}={e}^{-i\hat{Q}\otimes \hat{P}}$ and ${\bar{C}}_{X}^{{\dagger} }={e}^{i\hat{Q}\otimes \hat{P}}$. To simplify the numerical analysis, the noise of the approximate GKP state and the error introduced in the error correction operation are modeled as independent Gaussian shifts of standard deviation σ, represented by the channel:

$${{{\mathcal{E}}}}{(\hat{\rho })}_{\sigma }=\frac{1}{2\pi {\sigma }^{2}}\int\,{{{{\rm{d}}}}}^{2}\zeta {e}^{-| \zeta {| }^{2}/2{\sigma }^{2}}\hat{D}(\zeta )\hat{\rho }{\hat{D}}^{{\dagger} }(\zeta ).$$

(10)

The noise channel³⁵ is strictly diagonal on the displacement operator basis. Using displacement rotation (but not necessarily following a Gaussian distribution), arbitrary noise channels can be brought closer to the diagonal form equation (10) describes, for example, a noisy process with the same loss and heating rate, given by the main equation $\dot{\hat{\rho }}=\kappa \left({{{\mathcal{D}}}}[\hat{a}]\hat{\rho }+{{{\mathcal{D}}}}[{\hat{a}}^{{\dagger} }]\hat{\rho }\right)$. However, in a real system, the Gaussian displacement channel³⁶ generally does not represent the physical noise often encountered in oscillator systems, such as loss, dephasing, or heating at arbitrary rates, which requires further consideration.

Fig. 4: Stabilizer calibration circuit.

The light yellow in the surface-GKP code indicates that the calculated ground state corresponding to the X-type stabilizer is the $\left\vert {0}_{{{{\rm{gkp}}}}}\right\rangle$ stabilizer measurement line, and light blue indicates the calculation corresponding to the Z-type stabilizer. The ground state is $\left\vert {1}_{{{{\rm{gkp}}}}}\right\rangle$ stabilizer measurement line.

To further improve the information compression performance, we denote the squeezing parameter ${{{\mathcal{S}}}}$ as ${{{\mathcal{S}}}}=-10{\log }_{10}(2{\sigma }^{2})$ (with the identification Δ² = 2σ²) to quantify the noise in equation, with large ${{{\mathcal{S}}}}$ meaning low noise. When the Gaussian displacement channel introduces the noise of each element of the GKP codeword and error correction circuit, when GKP uses Steane-based error correction, it is found that the threshold standard deviation of the displacement error is ${{{\mathcal{S}}}}=18.6$ dB. To compress the noise threshold, we limit the squeezing parameter search to a maximum of 10 dB of squeezing.

With very advanced optical compression in ref. ³⁷, we found that the best fidelity is achieved by saturating the compression to 10 dB in at least one mode, increasing the response to larger search for compressed values. In Fig. 5, we plot the Wigner function of $\left\vert {0}_{\Delta }\right\rangle$ with Δ = 10 dB, and the Wigner function of the optimal state (highest fidelity) output by the three-mode circuit, $\left\vert {0}_{\Delta }\right\rangle$ designed to generate ${n}_{\max }=$ 4, 6 and 12 photons. We see that as ${n}_{\max }$ decreases and core state resources reduce, the number and sharpness of peaks keep away $\left\vert {0}_{\Delta }\right\rangle$, and remove the origin of the phase spacein difference minimum. In other words, as long as the standard deviation of the displacement error is less than 0.09, logic qubits with arbitrarily small error probability can be realized, but at the same time, it brings huge overhead and it is difficult to provide hardware support. To this end, we design a novel Steane error correction scheme and neural network decoder to reduce hardware overhead by improving error correction performance and decoding efficiency.

Fig. 5: Wigner function at different photon numbers.

a The figure shows a standard diagram of the Wigner function for $\left\vert {0}_{\Delta }\right\rangle$ at ${n}_{\max }=10$ with compression noise below 10 dB. From b to d, it can be seen that as ${n}_{\max }$ decreases, the number of peaks becomes less and less (the darker color indicates that the number of peaks here is more, and the noise reduction effect is better). In addition, from left to right, it can be seen that the phase space state after projection (bottom illustration, the darker the color is closer to the origin, the closer to the $\left\vert {0}_{\Delta }\right\rangle$ state) becomes more and more dispersed, and the difference is getting bigger and bigger. It follows that the number and sharpness of peaks are closer to $\left\vert {0}_{\Delta }\right\rangle$ at ${n}_{\max }=10$.

Error model

The qubit model in this paper is proposed based on the Gaussian random distribution function³⁸, and we give priority to the Gaussian error displacement channels ${{{{\mathcal{N}}}}}_{1},{{{{\mathcal{N}}}}}_{2}$, and ${{{{\mathcal{N}}}}}_{m}$ in ref. ⁸. The other components in the circuit are assumed to be noise-free, that is, the CNOT gate and the initial auxiliary qubit are perfect. Auxiliary qubits have the following two functions: one is used for surface-GKP code error correction, and the other is used for stabilizer checking (symon measurement). When affected by the channel of Gaussian error displacement error, the measurements made in this paper can be regarded as perfect homodyne measurements in $\hat{q}$ or $\hat{p}$ quadrature. Since the surface code is CSS and has 1/2 free rotation, the errors in X and Z are corrected independently, and the two are interoperable. Therefore, this paper only analyzes the Gaussian displacement error of $\hat{q}$ and the X stabilizer check in detail, and the Z stabilizer check is the same. Two error models are considered in the surface-GKP code error correction protocol³⁹. The first model has perfect measurements but noisy data GKP qubits. In the second model, both the data GKP qubits and the measurements are noisy. In the first noise model, the GKP error correction and auxiliary measurements in the stabilizer check are both perfect, ${{{{\mathcal{N}}}}}_{2}=I$ and ${{{{\mathcal{N}}}}}_{m}=I$, where I is the identity operator. This error model corresponds to the code capacity error model⁴⁰, where only data qubit errors are considered. The decoding process is implemented after a single round of X or Z stabilizer checks. In Fig. 4, each data GKP qubit has a Gaussian error shift error u₁ from the Gaussian error shift channel ${{{{\mathcal{N}}}}}_{1}$. Error correction is then performed on each data GKP qubit. The displacement u₁ will be propagated through the CNOT gate to the GKP auxiliary qubit.

In the second noise model, the Gaussian error displacement channel ${{{{\mathcal{N}}}}}_{1}$ in the data qubit and the auxiliary qubit in the measurement ${{{{\mathcal{N}}}}}_{2}$ and ${{{{\mathcal{N}}}}}_{m}$ also exist. The Gaussian error displacement channels ${{{{\mathcal{N}}}}}_{2}$ and ${{{{\mathcal{N}}}}}_{m}$ are located behind the CNOT gate, so there is no error propagation from the auxiliary qubits to the data qubits, which corresponds to the phenomenological error model⁴¹. After applying ME-Steane error correction, each data GKP qubit is not fully corrected but carries a displacement error u₁ − η(u₁ + u₂), where u₂ is the error of the GKP auxiliary qubit from ${{{{\mathcal{N}}}}}_{2}$. This noise model corresponds to the phenomenological error model. Since the Gaussian error displacement channels ${{{{\mathcal{N}}}}}_{2}$ and ${{{{\mathcal{N}}}}}_{m}$ are located after the CNOT gate, no auxiliary qubit to data qubit will generate error propagation. After we apply the novel Steann error correction, each data GKP qubit is not fully corrected but has a displacement error u₁ − η(u₁ + u₂), where u₂ is the error of the GKP ancilla qubit from ${{{{\mathcal{N}}}}}_{2}$.

Since the stabilizer inspection is faulty, the stabilizer inspection process should usually be repeated d times, where d is the color-coded distance. In each round of stabilizer checks, we consider the effects of Gaussian error displacement channels ${{{{\mathcal{N}}}}}_{1}$, ${{{{\mathcal{N}}}}}_{2}$, and ${{{{\mathcal{N}}}}}_{m}$. At the same time, it is assumed that the last round of measurements are perfect in both GKP error correction and stabilizer checks. This assumption is to ensure that the final GKP state is back in code space so that one can successfully decode the code or produce an accurate color-coded logical error X_L. After applying the new Steann error correction, the stabilizer measurement cannot be completely corrected, and multiple decoding checks are required at this time, usually repeated d times, where d is the surface code distance. The periodic surface code is re-evaluated for the effect of the Gaussian error displacement channels ${{{{\mathcal{N}}}}}_{1},{{{{\mathcal{N}}}}}_{2}$, and ${{{{\mathcal{N}}}}}_{m}$ in each round of stabilizer checks. After multiple decoding measurements, we assume that the GKP data qubits and stabilizer measurements⁴² are noise-free in the last inspection result, realizing that the GKP quantum states with errors are brought back into the code space. From this, we can successfully decode the surface-GKP code or correct the logical error X_L.

Simulation analysis

Therefore, for the above decoding process, we obtained the threshold display of the surface-GKP code. As shown in Fig. 6, the threshold value under the first noise model is 0.35, in contrast, the threshold value of the second noise model is lower, that is, the decoded data is usually in the qubit overhead. and decoding speed is difficult to meet our needs.

Fig. 6: Schematic diagram of threshold value under MWPM decoder.

a The left picture is the rendering of MWPM decoder for the first error type, in which the green square, purple circle, blue diamond, and yellow triangle represent surface-GKP codes with code distances of 5, 7, 9, and 11, respectively. The σ represents the standard deviation of the stea error correction scheme, which is also expressed as the physical error rate by the Gaussian noise random channel. b The threshold in this figure can be seen from the right panel to be 0.50, and the right image is for the stabilizer measurement. Thresholding effect of the second error type MWPM decoder combined with Dijkstra’s algorithm, it can be clearly seen that the threshold is much lower at 0.25.

According to the above two models of low-performance decoder and pure error decoder, it corresponds to the threshold display under the low-performance decoder on the left side of Fig. 7 and the threshold display under the pure error decoder on the right. The threshold of the low-performance decoder is raised from 0.50 to 0.78 compared with the threshold under MWPM, which is greatly improved due to the improvement of the accuracy of the decoder model and the convolution operation of the neural network, and the effect of the threshold improvement is more obvious when the code distance increases.

Fig. 7: Schematic diagram of threshold value under neural network decoder.

a The image on the left shows the low-performance decoder under the neural network decoder for the first error type. b The effect on the right shows that the threshold effect for the second noise model under the pure error decoder is 0.34.

Compared with the threshold of the pure error decoder, we can see that the threshold is only 0.34, but it is much higher than that of the MWPM universal decoder. Under the pure error, the error correction of the decoder is concentrated at the highest level of the training model, which can maintain a good error correction state. The neural network decoder uses the feedforward neural network⁴³ full connection method, its input is that all the correctors and the output is one of the three possible logic errors. Compared with the MWPM decoding algorithm, they can get a higher threshold and do not need to do repetitive training. After getting the given training model, we only need to input all the correctors independently to get the final output. And it can adapt to many error models in the training process, and may even be tailored to specific qubit technology or even a single quantum computing sample.

Discussion

This paper effectively solves the problem that the GKP boson error correction code cannot achieve fault tolerance when the shift error is greater than $\sqrt{\pi }/2$ by combining the surface code with GKP, and the standard deviation parameter is introduced into the error correction scheme. A modification of the traditional Stean-type scheme takes into account the actual error situation, and compressing the threshold channel to 10 dB shows a good form of denoising. In order to solve the inconsistency between the two kinds of noise cases, this paper proposes a general-purpose MWPM decoder and Dijkstra’s algorithm for fusion, which improves the threshold level of surface-GKP codes. What is more effective is that this paper proposes an error correction code decoding scheme based on neural network decoder, which improves the decoding rate by 50% and improves the decoder threshold level from 0.50 to 0.78 under low performance. A large leap has been achieved.

The threshold under the pure error decoder achieves a good fault tolerance effect for the two error models, and the threshold level has achieved a breakthrough of more than 0.3, which is based on the paper¹⁷. The limit decoder failed to achieve decoding effect. We still need to conduct in-depth research on bose quantum error correction, and further deepen the hardware overhead and training layers of machine learning to obtain better decoding results, so as to ensure that quantum computers have better fault tolerance in the running process.

Methods

ME-Steane type GKP error correction scheme

The traditional Steane error correction scheme is affected by the Pauli rotation approximation in the noisy GKP quantum state, and its mixed quantum state is as follows:

$$\int\,du\int\,dv{P}_{\sigma }(u){P}_{\sigma }(v){e}^{-iu\hat{p}}{e}^{iv\hat{q}}\left\vert \bar{\psi }\right\rangle \left\langle \bar{\psi }\right\vert {e}^{-iv\hat{q}}{e}^{iu\hat{p}}.$$

(11)

Ideally, all components of the circuit are noise-free except for the CNOT gates through which the auxiliary qubits that need to be measured go through. We give the initial state. From this we set the initial quantum state as:

$${e}^{-i{u}_{1}{p}_{1}}{e}^{-i{u}_{2}{p}_{2}}\left\vert \bar{\psi }\right\rangle \left\vert \bar{+}\right\rangle ,$$

(12)

The probability of u₁ and u₂ obeys a Gaussian random distribution function ${P}_{{\sigma }_{1}}({u}_{1})=\frac{1}{\sqrt{2\pi {\sigma }_{1}^{2}}}\exp (-\frac{{u}_{1}^{2}}{2{\sigma }_{1}^{2}})$ and ${P}_{{\sigma }_{2}}({u}_{2})=\frac{1}{\sqrt{2\pi {\sigma }_{2}^{2}}}\exp (-\frac{{u}_{2}^{2}}{2{\sigma }_{2}^{2}})$. The output quantum state after passing through the CNOT gate is:

$$\begin{array}{l}{e}^{-i{u}_{1}{p}_{1}}{e}^{-i({u}_{1}+{u}_{2}){p}_{2}}\left\vert \bar{\psi }\right\rangle \left\vert \bar{+}\right\rangle \\ \qquad= \frac{1}{\sqrt{N}}\mathop{\sum}\limits_{n\in {\mathbb{Z}}}{e}^{-i{u}_{1}{p}_{1}}\left\vert \bar{\psi }\right\rangle \left\vert q=n\sqrt{\pi }+{u}_{1}+{u}_{2}\right\rangle .\end{array}$$

(13)

where N is the normalization constant, and the syndrome measurement⁴⁴ result is ${q}_{out}=n\sqrt{\pi }+{u}_{1}+{u}_{2}$. The correction ${q}_{cor}={q}_{out}\,{{{\rm{mod}}}}\sqrt{\pi }$ is given by introducing the traditional Steane error correction scheme. Under the premise that σ₂ is much smaller than σ₁, the shift error u₂ is negligible and the error u₁ can be corrected:

$${q}_{cor}={u}_{1}+2k\sqrt{\pi },$$

(14)

where k is an integer. Thus, the conditional error probability given q_out is:

$$p(\bar{X}| {q}_{out})=1-\frac{{\sum }_{k}{P}_{{\sigma }_{1}}({q}_{out}-2k\sqrt{\pi })}{{\sum }_{k}{P}_{{\sigma }_{1}}({q}_{out}-k\sqrt{\pi })}.$$

(15)

For considering the influence of actual noise and solve the situation caused by the shift error u₂, we update the error probability distribution of u₁ to ensure that the best choice for correcting q_cor can be found, the actual q_out output probability is:

$$f({u}_{1},{q}_{out})=\frac{{P}_{{\sigma }_{1}}({u}_{1}){\sum }_{k}{P}_{{\sigma }_{2}}({q}_{out}-k\sqrt{\pi }-{u}_{1})}{{\sum }_{k}{P}_{{\sigma }_{12}}({q}_{out}-k\sqrt{\pi })},$$

(16)

where ${\sigma }_{12}=\sqrt{{\sigma }_{1}^{2}+{\sigma }_{2}^{2}}$ is the variance of the variable w = u₁ + u₂. We are satisfied that the correction is that f(u₁, q_out) can be decomposed into Gaussian distribution functions with different weights:

$$f({u}_{1},{q}_{out})=\frac{{\sum }_{k}{w}_{k}\exp \left[-\frac{{({u}_{1}-\eta ({q}_{out}-k\sqrt{\pi }))}^{2}}{2{\sigma }^{2}}\right]}{2\pi {\sigma }_{1}{\sigma }_{2}{\sum }_{k}{P}_{{\sigma }_{12}}({q}_{out}-k\sqrt{\pi })},$$

(17)

where $\eta =\frac{{\sigma }_{1}^{2}}{{\sigma }_{1}^{2}+{\sigma }_{2}^{2}}$, ${\sigma }^{2}=\frac{{\sigma }_{1}^{2}{\sigma }_{2}^{2}}{{\sigma }_{1}^{2}+{\sigma }_{2}^{2}}$ and ${w}_{k}=\exp \left[-\frac{(\eta -{\eta }^{2}){({q}_{out}-k\sqrt{\pi })}^{2}}{2{\sigma }^{2}}\right]$. From this, we can clearly find that the peak value of the Gaussian function ${u}_{1}=\eta ({q}_{out}-k\sqrt{\pi })$ and the largest function point f(u₁) is ${u}_{1}=\eta ({q}_{out}\,{{{\rm{mod}}}}\sqrt{\pi })$. After updating the weights, the maximum likelihood estimate of the shift error u₁ is ${q}_{cor}^{(ME)}=\eta ({q}_{out}\,{{{\rm{mod}}}}\sqrt{\pi })$. After we obtain the maximum likelihood estimate of the novel Steane error correction scheme, the conditional probability of Pauli-X error is:

$${p}^{{\prime} }(\bar{X}| {q}_{out})=1-\mathop{\sum}\limits_{k}\int\nolimits_{2k\sqrt{\pi }-\frac{\sqrt{\pi }}{2}}^{2k\sqrt{\pi }+\frac{\sqrt{\pi }}{2}}f({u}_{1}+{q}_{cor}^{(ME)},{q}_{out})d{u}_{1}.$$

(18)

Correction ${q}_{cor}^{(ME)}$ is half of where σ₂ = σ₁$(\eta =\frac{1}{2})$ in a specific case q_cor. When σ₂ ≪ σ₁, the parameter η ≈ 1 in the maximum likelihood estimation of our shift error u₁, that is, the new Steane error correction scheme, is consistent with the traditional error correction scheme⁴⁵ (the formula can be obtained out, σ₂ → 0). When the second case occurs, that is, when the surface-GKP code has no other noise except for measuring auxiliary qubits, it continues to use the traditional Steane error correction scheme.

To characterize the performance of the novel error correction code, we cite a function as a demonstration of the error correction performance of GKP. Surface-GKP error correction⁴⁶ with perfect (noise-free) auxiliary qubits corresponds to the mapping of the shift error u₁ in the data qubits:

$$\pi ({u}_{1})=\left\{\begin{array}{lll}0,&&{{{\rm{if}}}}\,| {u}_{1}\,{{{\rm{mod}}}}2\sqrt{\pi }|\, < \,\frac{\sqrt{\pi }}{2};\\ \sqrt{\pi },&&{{{\rm{otherwise}}}}.\end{array}\right.$$

(19)

This means that the data qubit error u₁ becomes π(u₁) after the noise-free surface-GKP error correction. We can get that any small error u₁ can be corrected, while a large shift error u₁ may cause $\sqrt{\pi }$($\bar{X}$ error), which will affect measurements to the next level of stabilizer code. Similarly, when the auxiliary qubit is noisy, the mapping ${\pi }^{{\prime} }({u}_{1})$ of the Steane-type error correction scheme is

$${\pi }^{{\prime} }\left({u}_{1}\right)={u}_{1}-{q}_{cor}$$

(20)

Then we define the function $\Delta ({\pi }^{{\prime} },\pi )$ to measure the difference between the noiseless surface-GKP error correction and the noisy GKP error correction scheme, where the angle brackets denote all Gaussian variables u₁ and Gaussian weighted average of u₂. In order to find the optimal ${q}_{cor}^{(ME)}$ value and show it as the optimal correction scheme, we give different q_cor to simulate $\Delta ({\pi }^{{\prime} },\pi )$, it can be found from Fig. 8 that ${q}_{cor}^{(ME)}$ is the optimal selection condition to minimize $\Delta ({\pi }^{{\prime} },\pi )$.

Fig. 8: Steane type error correction scheme.

the red histogram in the figure indicates that $\Delta ({\pi }^{{\prime} },\pi )$ is a schematic diagram of Steane type error correction adjustment; The light blue histogram represents a schematic diagram of Steane type error correction adjustment when ${\sigma }_{1}^{2}$ is twice as much as ${\sigma }_{2}^{2}$; the dark blue histogram represents ${\sigma }_{1}^{2}$ is a schematic diagram of Steane type error correction adjustment in the case of four times ${\sigma }_{2}^{2}$. From the figure we can see that ${Q}_{COR}={Q}_{COR}^{(ME)}$ is the best correction to minimize $\Delta ({\pi }^{{\prime} },\pi )$.

After completing the new Steane error correction scheme, the problem of whether the maximum likelihood estimation of shift error still exists under coherent noise⁴⁷ is also solved. As can be seen from the formula, the pure quantum state is the same as the correction of ${q}_{cor}^{(ME)}$ above, resulting in consistent results. Therefore, we have obtained the optimal error correction conditions. Next, we need to perform decoding operations from surface-GKP error correction codes of different dimensions, and have obtained the maximum possible information protection and recovery operations.

Threshold is an important representative of the performance of physical qubits in line gate transmission. When the physical error rate is lower than a certain threshold, a quantum computer can suppress the logical error rate to an arbitrarily low level by applying a quantum error correction scheme. The threshold level is affected by the error noise model and decoding performance. We introduce two error noise models for the surface-GKP code and propose a comparison of two different decoding methods for the noise models, one is a MWPM decoder⁴⁸ where vertex matching can be done in one polynomial time, and the other is a neural network decoder that can decode in all directions using 2D matrices and convolution operations.

MWPM decoder

In order to improve the decoding performance and reduce the qubit overhead⁴⁹, we propose a general decoder for the above two error models based on¹⁷. The MWPM decoder can restate the noise model as a mathematical model: for a given syndrome geometry (all vertices in Fig. 6), the decoder can find a set of identical syndromes (set of lattices). In order to ensure that the quantum state information is not destroyed, we need to make the corrected qubit the same as the error qubit of the stabilizer, so as to avoid logical errors X_L and Z_L. For the two error noise models, it is difficult for us to find an effective maximum likelihood decoder (MLD). The combined GKP code measurement results are not binary, but continuous variable information, which can provide more logical error information. By computing q_out, we can get the average error probability of all GKP qubits:

$$\bar{p}=1-\mathop{\sum}\limits_{n\in {\mathbb{Z}}}\int\nolimits_{2n\sqrt{\pi }-\frac{\sqrt{\pi }}{2}}^{2n\sqrt{\pi }+\frac{\sqrt{\pi }}{2}}{P}_{\sigma }(x)dx.$$

(21)

It is obvious that it is not $\bar{p}$ that we want to find the maximum likelihood correction through the conditional error probability. To construct a general decoder model, the focus is on addressing the second error model where noise is present in both syndrome and stabilizer measurements. Since the results of the stabilizer check are unreliable, the measurements need to be repeated for d cycles. To this end, we apply MWPM decoder and Dijkstra’s algorithm to do 3D graph surface-GKP code matching in this paper to ensure maximum probability of detecting stabilizer measurement failures. The specific optimization description and performance display are described in detail in Supplementary Note 2: Optimize MWPM decoder. First, assuming that all components in the quantum circuit and the initial surface-GKP quantum state are noise-free, this paper performs the first round of stabilizer-free noise (the first error model) measurement cycle. Next, we add an additional ambient noise environment (the second error model) to measure the period under stabilizer noise, where the measurement period without noise is to ensure that the noise state can be restored to the code space, so as to determine whether the error correction is successful. Finally, we want to construct Z-type and the X-type 3D space-time graphs to represent the periodic results of a new round of stabilizer measurements. The detailed construction process is shown in Supplementary Note 1: Construction of 3D space-time graphs for decoding Z-type and the X-type of the syndrome output.

When we have constructed the 3D space-time map of the surface-GKP code from Supplementary Note 1: Construction of 3D space-time graphs, we use MWPM decoding algorithm to correct it:

• 1: Perform d rounds of noise stabilizer measurements on the initial GKP state, followed by a noise-free stabilizer measurement to construct the Z-type and the X-type 3D space-time diagram as shown in the figure;

• 2: Highlight the vertices in the assigned stabilizer value that are compared with the previous round. To ensure that the number of vertices is an even number, mark the boundary vertices when the number of vertices in the space-time graph is odd;

• 3: Using Dijkstra’s algorithm, we can find the minimum weight matching for both the Z-type and the X-type vertices highlighted by the markers. Connect matching vertices with solid lines to highlight the optimal weight path;

• 4: For the convenience of calculation, we need to project the 3D space-time map of the vertical side onto the 2D plane. Count the number of display times for each Z-type and the X-type horizontal boundary. If the horizontal boundary is highlighted, it will not be processed; otherwise, we will count the data of Z-type and the X-type Error correction for GKP qubits ${\hat{X}}_{{{{\rm{gkp}}}}}$ (${\hat{Z}}_{{{{\rm{gkp}}}}}$);

• 5: After the correction is completed, only the noise effect of the data qubit under the second noise model remains, corresponding to ${\xi }_{q}^{D}=({\xi }_{q}^{(D1)},\cdots \,,{\xi }_{q}^{(D{d}^{2})})$ and ${\xi }_{p}^{D}=({\xi }_{p}^{(D1)},\cdots \,,{\xi }_{p}^{(D{d}^{2})})$. Define ${{{\rm{total}}}}({\xi }_{q}^{D})\equiv \mathop{\sum }\nolimits_{k = 1}^{{d}^{2}}{\xi }_{q}^{(Dk)}$ and ${{{\rm{total}}}}({\xi }_{p}^{D})\equiv \mathop{\sum }\nolimits_{k = 1}^{{d}^{2}}{\xi }_{p}^{(Dk)}$. Then, we determine that there is

  $$\left\{\begin{array}{ll}{{{\rm{Pauli}}}}\,X\quad &{{{\rm{total}}}}({\xi }_{q}^{D})={{{\rm{odd}}}}\,\& \,{{{\rm{total}}}}({\xi }_{p}^{D})={{{\rm{even}}}}\\ {{{\rm{Pauli}}}}\,Z\quad &{{{\rm{total}}}}({\xi }_{q}^{D})={{{\rm{even}}}}\,\& \,{{{\rm{total}}}}({\xi }_{p}^{D})={{{\rm{odd}}}}\\ {{{\rm{Pauli}}}}\,Y\quad &{{{\rm{total}}}}({\xi }_{q}^{D})={{{\rm{odd}}}}\,\& \,{{{\rm{total}}}}({\xi }_{p}^{D})={{{\rm{odd}}}}\end{array}\right.$$

  (22)

  error. Otherwise if both ${{{\rm{total}}}}({\xi }_{q}^{D})$ and ${{{\rm{total}}}}({\xi }_{p}^{D})$ are even, there is no logical error.

Neural network decoder

In order to get a high-performance decoder and run fast enough to avoid problems such as data squeezing. The advent of neural networks brought a new dawn to error correction decoding. In this paper, an efficient decoding scheme of surface-GKP codes based on neural network decoder is proposed (the specific construction process of neural networks can be found in the literature). To accommodate the error-free model, we propose two independent neural network decoder schemes. One is a neural network decoder suitable for low-error levels. For example, the first error model in the above error model only has data qubit errors, and only the generated syndrome can be used as an output to obtain data qubits. The other is an advanced neural network decoder that combines a neural network decoder with a pure error decoder, where the pure error decoder (see Supplementary Note 3: Pure Error Decoder) contains both data qubits and stabilizer measurement errors, and the logic error is output by the neural network decoder, as follows:

Generate a true error model for training the neural network’s decoder model⁵⁰. Noise model sampling is required for data qubit errors (the impact of both models is the same, and the depolarized noise model is used here for convenience). First, avoiding the additional meaningless overhead of the decoder choosing a noise model that measures no errors, it is necessary to apply a random number in each cycle from the X, Y, or Z errors by depolarizing the noise model selection physical error to achieve. It is not pre-generated test data and training set, it is done dynamically before the neural network convolution in ref. ⁵¹. Second, so as to avoid data overfitting, the syndrome and logic errors generated by the decoder are used for training, and the performance is better when the code distance is less than 7, but when the distance is too large, the syndrome set is huge, and the training data set will cause too much volatility, which is difficult to correct. In this paper, the data is generated by simulation, and the data is kept dynamically refreshed, and the amount of data is not limited. Therefore, it avoids the interference of data correlation on error correction, and successfully reduces the problem of data over-fitting⁵². These data sets are then fed into the simulator of the surface-GKP code to obtain the corresponding error syndromes. Finally, the generated set of syndromes is passed to a low-level neural network decoder and an error-only decoder. The pure error is compared with the actual data qubit, and the logical difference between the two is used as the output target value of the neural network.

In the training process, we used batch size 5122 blocks (combined with the data support provided by the literature⁵³), and did not recycle the data set. In order to speed up the training speed, we trained 3 × 10⁵ batches of neural network elements. The neural network unit determines that the total data set for each training is 1.8 × 10⁹. Figure 9 shows the training effect on the neural network unit 2 × 10³ batches, it can be seen from the figure that the number of iterations reaches performance saturation after 180 iterations. To ensure the accuracy of the model, we do the training test again after the training is completed, and continue to use the 2 × 10³ batch of neurons for statistics. It can be seen from Fig. 9(b) that the error fluctuates between 0.12–0.15, the fitting degree of the data reaches more than 98%. To demonstrate the different performance on overhead in detail, this paper shows the decoding performance of different transfer functions. This work is detailed in Hyperbolic Tangent (TanH)^47,48, Corrected Linear Unit (ReLU)^54,55, and Extended Nonlinearity (SQNL) as follows :

$${{{\rm{TanH}}}}(x)=\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$$

(23)

$${{{\rm{ReLU}}}}(x)=\left\{\begin{array}{ll}0,\quad {{{\rm{for}}}}\,x \,<\, 0\\ x,\quad {{{\rm{for}}}}\,x \,\ge\, 0\end{array}\right.$$

(24)

$${{{\rm{SQNL}}}}(x)=\left\{\begin{array}{ll}-1,\qquad\quad {{{\rm{for}}}}\,x < -1\\ 2x+{x}^{2},\quad {{{\rm{for}}}}\,\,-1\le x\, < \,0\\ 2x-{x}^{2},\quad {{{\rm{for}}}}\,0\le x\le 1\\ 1,\qquad\quad\,\,\,\, {{{\rm{for}}}}\,x \,>\, 1\end{array}\right.$$

(25)

To avoid introducing new false noise, the transfer function chosen by each node is the same.

Fig. 9: Schematic diagram of neural network decoder training.

a As the number of iterations on the abscissa increases, the training performance of different transfer functions can be seen. b The performance of the SQNL purple graph is the best, but it reaches saturation when the number of iterations reaches 150.

Table. 1 compares the performance of different transfer functions, similar to the comparison of rotational symmetry. Take the computationally expensive hyperbolic tangent as a reference, the average performance difference between ReLU and TanH is not significant. Since ReLU is much cheaper in hardware overhead implementation (doesn’t need any exponential), this paper mainly adopts ReLU. From Fig. 9 and Table 1, we can see that the transfer function shows an amazing increase in the performance of fit at larger code distances, which indicates that a larger number of neural network layers is required to provide code training with larger distances. Based on the above data analysis, we adopted a movable neural network with SQNL function, which made up for the lack of iterative depth of the neural network, thus we obtained a neural network decoder with high fitting accuracy, low hardware overhead, and fast correction speed. The construction of the training model and the quantization error optimization process, as well as the superiority of the transfer function SQNL, see Supplementary Note 4: Training optimization.

Table 1 Training with different transfer functions on a surface code lattice with one-half degree of freedom of rotation, showing performance on different layers.