Introduction

Degenerative cervical myelopathy (DCM) describes a spectrum of age-related diseases of the cervical spine [1]. It is defined as a symptomatic dysfunction of the spinal cord caused by compression due to one or more etiologies including spondylosis/congenital stenosis, disc herniation, ossification of the posterior longitudinal ligament, hypertrophy of the ligamentum flavum, and degenerative subluxation [2]. DCM is the most common cause of nontraumatic spinal cord dysfunction globally. New et al. estimated that DCM encompasses 59% of nontraumatic spinal cord injury (SCI) in Japan, 54% in the United States, 31% in Europe, 22% in Australia, and 4–30% in Africa [3]. Prevalence of radiographic cord compression in asymptomatic volunteers (5.3%) highlights the importance of correlating imaging findings with clinical signs and symptoms [4].

A detailed diagnosis of the cervical spine in DCM patients is usually performed using axial and sagittal plane magnetic resonance (MR) images. Different methods for the estimation of canal stenosis on MR imaging have been reported throughout the literature. Initial attempts used proxies such as counting the number of compression sites, spinal cord occupation rate, maximum canal compromise (MCC), maximum spinal cord compression (MSCC), compression ratio (CR), and the absolute axial cross-sectional area (CSA) of the cord at the site of compression [4,5,6,7,8,9,10,11,12]. Irrespective of the metric used, these measurements aim to determine the severity of the cord compression at the level of stenosis. Highlighting that “true” stenosis is defined by the relationship between the cord and the canal (i.e., if the spinal cord is thin, and there is room in the spinal canal, then stenosis cannot be concluded), Kato et al. proposed the measurement of “occupation rate” defined as the ratio of the diameter of the cord to that of the canal in the mid-sagittal plane [4].

In the axial plane, CR is defined as the ratio of the anteroposterior (AP) cord diameter to the transverse (TR) cord diameter. However, CR has limited use in assessing circumferential compression, i.e., simultaneous compression in the sagittal and coronal planes [13]. Absolute CSA of the cord is useful in quantifying cord compression in such cases when there is a change in cord dimensions without any corresponding change in shape. Recognizing that canal and cord dimensions vary between individuals, Fehlings et al. highlighted that any measurement at the stenotic level must be normalized with respect to the normal adjacent levels [12]. Using mid-sagittal MR scans, metrics MSCC and MCC were developed to assess normalized cord and canal dimensions respectively at the level of injury, by making comparisons with the nearest normal mid-vertebral cephalad and caudal levels [12]. Although MSCC and MCC metrics have been developed and used extensively in the context of traumatic cervical SCI, validation of these metrics is required for assessing DCM patients [5, 6].

In an individual, geometrical variations exist in the cervical spinal canal and the cord along the rostrocaudal axis. In addition, there are geometrical variations amongst individuals that are attributable to various factors including age, sex, and body height [14]. Ulbrich et al. estimated normative values for sagittal diameter and TR area of the cord and the canal at C1, C3, and C6 levels for men and women, 45 years of age, in three different body height subgroups (1.50, 1.70, and 1.90 m) [14]. The authors found a wide variation in results, which highlighted the challenges with defining subject-specific normal values, even when factors including age, sex, and body heights are taken into account. We posit that for a metric used to quantify the severity of cervical stenosis, patient-specific normal values must be estimated for the stenotic level first. Deviation of the measured value from the estimated normal value will provide an explicit measure of the severity of cervical stenosis controlling for the variations attributable to cervical level, age, sex, and body height. This will also allow for comparisons to be made between various metrics regarding their SC (a cornerstone of an ideal metric). The other cornerstone for any useful measurement tool is its reliability or reproducibility, i.e., the level of consistency of repeated measurements by the same rater (intrarater reliability) and different raters (interrater reliability).

Therefore, the main objective of this retrospective cross-sectional study was to assess the SC and reliability of various mid-sagittal and axial plane metrics in the assessment of patients with single-level degenerative cervical stenosis on T2-weighted MR imaging. Patient-specific normal values for the metrics were estimated for the stenotic level using values measured at the nonstenotic cephalad and caudal levels. Deviation of the measured value from estimated normal value was calculated to assess the severity of stenosis and compare the potential of the metric for detecting change (SC). Interobserver and intraobserver reliabilities of the metrics were also assessed.

Methods

With prior approval from the University of New South Wales—Human Research Ethics Advisory Panel (UNSW-NRR-HC17222), a retrospective cross-sectional study of the MR images of patients who had presented for a scan of their cervical spine between September 2010 and August 2017 at the imaging facilities of Healthcare Imaging Services (St. Leonards, NSW, Australia) was conducted.

Patients

The inclusion and exclusion criteria for selecting patient records for the present study were as follows.

Inclusion criteria: age ≥ 18 years; evidence of nontraumatic, degenerative changes in the cervical spine, including disc desiccation, disc herniation, posterior osteophytes, flaval hypertrophy, and ossification of the posterior longitudinal ligament at one or more cervical levels; cervical stenosis at no more than one level, defined as a change in spinal cord contour at the level of an intervertebral disc on mid-sagittal MR scan; and nil compression, defined as nil canal compromise or cord indentation, at adjacent cephalad and caudal levels (to serve as controls).

Exclusion criteria: patients with a history of surgical intervention to the cervical canal or the cord; nondegenerative cord compression (e.g., tumorous or traumatic); and patients with multilevel compression, where adjacent cephalad and caudal levels show canal compromise and/or cord indentation.

A total of 85 de-identified T2-weighted MR imaging records of patients with single-level degenerative cervical stenosis were consecutively selected from the digital archives of Healthcare Imaging Services. The exclusion of patients with multilevel cervical stenosis facilitated comparison of stenotic values with adjacent nonstenotic levels giving patient-specific controls and normalizing for variables including age, sex, and height.

Measurements on T2-weighted MR images

T2-weighted MR images were selected for the assessment of cord compression and spondylotic changes because of the high contrast and sharpness of the cord-cerebrospinal fluid interface, thus clearly delineating cord and canal margins. Spondylotic changes assessed included osteophyte disc complexes, flaval hypertrophy, and severity of disc degeneration. Prior to interpretation, all the MR images were de-identified and randomly numbered from 1 to 85 by an administrative person unrelated to this research. The de-identified images were procured in JPEG file format, as a set of four images for each patient. This included images from the mid-sagittal plane and the axial plane at the stenotic level and the nonstenotic cephalad and caudal levels.

Assessment of cervical stenosis

The degree of degenerative cervical stenosis on T2-weighted MR scans was quantified through geometrical measurements in the sagittal plane and the axial plane images (Figs. 1 and 2). All the MR images were analyzed using imaging software tool ImageJ (vers. 1.51, US National Institutes of Health, Bethesda, MD, USA). The geometrical measurements were made at the three levels of interest: level of stenosis, nonstenotic cephalad, and caudal levels.

Fig. 1
figure 1

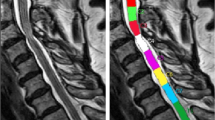
Mid-sagittal T2-weighted magnetic resonance images of a patient with single-level degenerative cervical stenosis. a, b \({\mathrm{M}}_{1} = {x}_{0}/{y}_{0}\), where \({x}_{0}\) is the cord diameter and \({y}_{0}\) is the canal diameter at the level of stenosis. c \({\mathrm{M}}_{2} = {x}_{0}/(0.5 {\times}({x}_1+{x}_{2}))\), where \({x}_{0}\) is the cord diameter at the level of stenosis, and \({x}_{1}\) and \({x}_{2}\) are the cord diameters at the mid-vertebral cephalad and caudal levels, respectively. d \({\mathrm{M}}_{3} = {y}_{0}/(0.5 {\times}({y}_1+{y}_{2}))\), where \({y}_{0}\) is the canal diameter at the level of stenosis, and \({y}_{1}\) and \({y}_{2}\) are the canal diameters at the mid-vertebral cephalad and caudal levels, respectively

Full size image
Fig. 2
figure 2

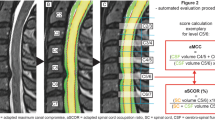
Axial T2-weighted magnetic resonance images of a patient with single-level degenerative cervical stenosis. a \({\mathrm{M}}_{4} = {x}/{y}\), where x is the anteroposterior diameter and y is the transverse diameter of the cord. b M5 = A, where A represents the absolute cross-sectional area of the cord as enclosed by the free-hand contour

Full size image

In the mid-sagittal plane, the following metrics were evaluated (Fig. 1):

Metric 1 (M1): Ratio of cord diameter to canal diameter;

Metric 2 (M2): Ratio of cord diameter to the average of mid-vertebral cephalad and caudal cord diameters;

Metric 3 (M3): Ratio of canal diameter to the average of mid-vertebral cephalad and caudal canal diameters.

In the axial plane, the following metrics were evaluated (Fig. 2):

Metric 4 (M4): Ratio of cord AP diameter to cord TR diameter;

Metric 5 (M5): Absolute area of the cord.

Geometrical changes along the rostrocaudal axis

Geometrical changes in the cervical spinal canal and the cord were examined along the rostrocaudal axis in all the 85 patients using the values obtained for the five metrics at the nonstenotic cephalad and caudal levels.

$$\mathrm{Morphological}\;\mathrm{variation}\;\Delta M_i\left(\%\right) = \left(1 - \frac{M_i\mathrm{caudal}}{M_i\mathrm{cephalad}}\right)\,\times\;100,$$
$$M_i(i = 1,2,3,4,5).$$

Sensitivity to change

SC for a metric was defined as the percentage deviation of the measured value from the patient-specific estimated normal value. The patient-specific estimated normal value for the given metric was calculated as the average of the values derived from nonstenotic cephalad and caudal levels

$$\mathrm{Sensitivity}\;\mathrm{to}\;\mathrm{Change}\;M_i({\mathrm{\% }}) = \frac{{M_i(\mathrm{stenotic}) - M_i(\mathrm{estimated}\;\mathrm{normal})}}{{M_i(\mathrm{estimated}\;\mathrm{normal})}}\,\times\;100.$$

Statistical analyses

For data analyses, statistical package SPSS (vers. 20, IBM Corporation, Armonk, USA) was used. The level of significance was set to 5% (α = 0.05). Normality assessment of the five MR metrics using the shape of the histograms and Shapiro–Wilk test revealed non-normality in the dataset. Therefore, nonparametric Friedman test was utilized for detecting significant differences between groups (level of stenosis, nonstenotic cephalad level, and nonstenotic caudal level). Post hoc analysis was conducted using Wilcoxon signed-rank tests with Bonferroni adjustment applied.

Two independent raters performed geometrical measurements on the spinal cord and the canal in all T2-weighted MR images. The first rater performed repeat measurements 3 weeks after the first measurements. The intrarater and interrater reliability were assessed by calculating intraclass correlation coefficients (ICC), with values <0.5, 0.5–0.75, 0.75–0.9, and >0.90 indicating poor, moderate, good, and excellent reliability, respectively [15, 16]. For interrater reliability analysis, ICC estimates and their 95% CI were based on single-rating, absolute-agreement, and two-way random-effects model. For intrarater reliability analysis, ICC estimates and their 95% CI were based on single-rating, absolute-agreement, and two-way mixed-effects model.

Results

Patient selection

Eighty-five consecutive patients (48 males and 37 females) satisfied the inclusion and exclusion criteria for this study. The average age of male patients at the time of MR scan was 58.56 (±12.70) years, and that of female patients was 57.51 (±13.46) years. The age range of patients was 25–93 years, and the median age was 58 years.

Cord compression across cervical levels showed a bimodal distribution, peaking at C5-6 level (n = 32, 37.6% of the patient cohort) and C3-4 level (n = 29, 34.1% of the patient cohort). Stenosis did not occur at C2-3 or C7-T1 levels in any of the 85 patients. More than half of the degenerative changes (53.6% of osteophyte disc complexes, 52.7% of flaval hypertrophy, and 58% of severe disc degeneration) occurred at C5-C6 and C6-C7 levels (Fig. 3).

Fig. 3
figure 3

Frequency distribution of various degenerative changes in the cervical spine of 85 single-level cervical stenosis patients assessed using T2-weighted magnetic resonance images. a Frequency distribution of osteophyte disc complexes at various cervical levels, b frequency distribution of flaval hypertrophy at various cervical levels, and c frequency distribution of the severity of disc degeneration at various cervical levels (based on Nil = 0; Mild = 1 or 2; and Severe = 3 or 4 from Sabnis et al. [25])

Full size image

Reliability analyses

The level of reliability for all the geometrical measurements on the spinal canal and the cord in the mid-sagittal plane was “moderate” to “excellent” for mid-sagittal plane measurements, and “poor” to “excellent” for axial plane measurements (Table 1).

Table 1 Interrater and intrarater reliabilities: intraclass correlation coefficient (ICC) and their 95% confidence interval (95% CI) for various geometrical measurements on mid-sagittal and axial T2-weighted MR scans of single-level cervical stenosis patients
Full size table

Average values at the level of stenosis and control levels

Average values (±standard deviation) for mid-sagittal and axial plane metrics, measured at the stenotic, and nonstenotic cephalad and caudal levels, are shown in Table 2. Rostrocaudal changes in metrics from normal cephalad to normal caudal levels were also determined in all 85 patients (Fig. 4). Although the average percentage change along the rostrocaudal axis across all the metrics was small (approximately −5%), the standard deviation was high compared with the average values (differences insignificant (P = 0.10) between mid-sagittal plane metrics M1, M2, and M3; differences insignificant (P = 0.588) between axial plane metrics M4 and M5). Along the rostrocaudal axis, the CSA of the cervical cord decreased in 47/85, increased in 28/85, and did not change (<1%) in 10/85 patients. The cord became more elliptical (decrease in CR) in 53/85, more circular (increase in CR) in 29/85, and did not change in 3/85 patients. The cord occupancy within the canal increased in 24/85, decreased in 56/85, and did not change in 5/85 patients. No consistent variation as such was observed in the cervical spinal canal and cord morphology along the rostrocaudal axis.

Table 2 Average (±standard deviation) values for T2-weighted magnetic resonance imaging based mid-sagittal plane (M1, M2, and M3) and axial plane (M4 and M5) metrics used for quantifying morphological characteristics of the cervical spine at the stenotic and nonstenotic (cephalad and caudal) levels in 85 patients with single-level cervical stenosis
Full size table
Fig. 4
figure 4

Change in the cervical spinal canal and cord geometry along the rostrocaudal axis quantified using T2-weighted magnetic resonance (MR) imaging based mid-sagittal plane (M1, M2, and M3) and axial plane (M4 and M5) metrics. Percentage change in the mid-sagittal and axial plane metrics were evaluated across all 85 patients, from normal cephalad to normal caudal levels. Polynomial trendlines of sixth order were also drawn to depict the trend. No trend as such was observed for geometrical changes in the cord and the canal along the rostrocaudal axis, neither with the mid-sagittal plane metrics (P = 0.100) nor with the axial plane metrics (P = 0.588)

Full size image

SC for metrics used for quantifying stenosis

Across all individual subjects (reflecting a range of stenosis severity), the SC data for mid-sagittal plane metrics M1 (16.64% ± 16.48%), M2 (−23.95% ± 11.12%), and M3 (−32.87% ± 10.60%) were significantly different (P = 0.000), and the post hoc analysis showed that all the pairwise comparisons were also significantly different (P = 0.000). Similarly, SC for M4 (−24.62% ± 12.17%) was significantly greater compared with the SC for M5 (−6.71% ± 11.08%) (P = 0.000) (Fig. 5).

Fig. 5
figure 5

Sensitivity to change (SC) for the mid-sagittal plane (M1, M2, and M3) and axial plane (M4 and M5) metrics used for quantifying the severity of single-level degenerative cervical stenosis on T2-weighted magnetic resonance (MR) images. Normal values for all the metrics at the level of stenosis were estimated by averaging the values measured at the nonstenotic cephalad and caudal levels. The SC for a given metric was calculated as the percentage deviation of the measured value from the estimated normal value at the level of stenosis. Polynomial trendlines of sixth order were also drawn to depict the trend in the SC for all the metrics. In the graphs, a vertical line drawn across a patient ID will give the SC for all the metrics used in the assessment of the same severity of stenosis. The SC data for mid-sagittal plane metrics were significantly different (P = 0.000), and the post hoc analysis showed all the pairwise comparisons were also significantly different (P = 0.000). The SC data for axial plane metrics were significantly different (P = 0.000). Metrics M3 and M4 were most sensitive in quantifying the severity of cervical stenosis

Full size image

Discussion

In this retrospective cross-sectional study of 85 patients with single-level degenerative cervical stenosis selected from a large MR database, we examined the SC and reliability of various mid-sagittal and axial plane metrics used for quantifying the severity of degenerative cervical stenosis on T2-weighted MR images. We further utilized these metrics to capture geometrical changes in the cervical spinal canal and the cord along the rostrocaudal axis.

Fehlings et al. developed and validated MSCC and MCC for assessing canal compromise and severity of cord compression in patients with acute cervical SCI [12]. The authors performed extensive reliability analyses and correlated the severity of cord compression and canal compromise with the baseline neurologic assessment using American Spinal Injury Association impairment scale [17,18,19,20]. Only one study (n = 17) has reported on the reliability of these metrics in assessing DCM patients and their correlation with the scores based on the modified version of the Japanese Orthopaedic Association scale [2]. To our knowledge, no study to date has reported on the SC of these MR-based metrics in the assessment of cervical stenosis.

Degenerative pathologies in our patient cohort peaked at C5-6 and C6-7 levels (Fig. 3), which is consistent with the data reported in the literature [21,22,23,24]. Cervical stenosis showed a bimodal distribution with the most frequent level being C5-6 (32/85) followed by C3-4 (29/85). When the nonstenotic cephalad and caudal levels were compared, no consistent variation was observed in the cord and canal geometry along the rostrocaudal axis (Fig. 4). The absence of any consistent trend suggests that the geometry of the cervical spinal canal and the cord is exclusive to the individual patient.

Therefore, for an accurate quantitative assessment of degenerative cervical stenosis, patient-specific normal values must be defined first at the level of stenosis, and only then the deviations should be captured from normality. In this study, we defined SC for a metric as the percentage deviation of the measured value from the estimated normal value. Normal values for all the metrics at the level of stenosis were estimated by averaging the values measured at the nonstenotic cephalad and caudal levels. The SC data allowed us to make an objective comparison of the ability of various MR metrics in capturing the same severity of cervical stenosis. Across all individual subjects (reflecting a range of stenosis severity), SC for all the five metrics was evaluated (Fig. 5). The distribution of the SC data closer to the horizontal axis (±10%) indicated a failure of the metric to capture cervical stenosis when it was indeed present (Fig. 5). We found that in the mid-sagittal plane, M1 failed to adequately capture cervical stenosis in 33/85, M2 in 10/85, and M3 in 1/85 patients. In the axial plane, M4 failed to adequately capture cervical stenosis in 8/85 and M5 in 48/85 patients. Our results suggest that in the mid-sagittal plane M3 is more sensitive to change compared with M1 and M2, and in the axial plane M4 is more sensitive to change compared with M5. Since M3 is a ratio of the canal diameter at the level of stenosis to the mid-vertebral cephalad and caudal canal diameters measured in the mid-sagittal plane, these results question the usefulness of sagittal plane cord dimensions in the assessment of cervical stenosis. The SC data for the axial plane metrics suggest that cervical stenosis results in cord distortion accompanied by a minimal change in the TR area of the cord. Perhaps, changes in the canal dimensions in the mid-sagittal plane and cord shape in the axial plane are more reliable indicators of canal stenosis on T2-weighted MR images. Interrater and intrarater reliabilities for measurements in the mid-sagittal plane ranged from “moderate” to “excellent.” In the axial plane, ICC estimates for the lateral diameter of the cord showed “excellent” reliability; however, the same was not true for the TR area and the AP diameter of the cord (Table 1).

Some limitations to the present study were noted. Only patients with single-level degenerative cervical stenosis were included to allow comparisons with nonstenotic adjacent levels. The relationship between the severity of stenosis and intensity of intramedullary cord signal change on T2-weighted MR images was not assessed. The prevalence of signal intensity change in patients with DCM has been reported in the range of 58–85% [13]. In contrast, it was recently reported that incidental signal intensity change occurred in 2.3% of asymptomatic Japanese volunteers [4]. Further research is needed to elucidate the relationship between the location of cervical stenosis and the region and the magnitude of the signal intensity change on MR scans. As the selections were made by the assessors conducting the study, there is a risk of selection bias. Also, being a purely imaging study, any correlation between stenosis (as measured by various metrics used in the study) and clinical symptoms was not examined. Lastly, differences in image quality, size, and resolution were a potential source of error and may explain the “poor” interrater and intrarater reliabilities recorded with some of the axial plane measurements.

In conclusions, our results show that the geometry of the cervical spinal canal and the cord is unique in each patient, and therefore, patient-specific normality must be established first for an accurate quantitative assessment of the severity of degenerative cervical stenosis. Changes in canal dimensions in the mid-sagittal plane and cord shape in the axial plane are more sensitive indicators of degenerative cervical stenosis on T2-weighted MR images.