State-conditional coherent charge qubit oscillations in a Si/SiGe quadruple quantum dot

Abstract

Universal quantum computation requires high-fidelity single-qubit rotations and controlled two-qubit gates. Along with high-fidelity single-qubit gates, strong efforts have been made in developing robust two-qubit logic gates in electrically gated quantum dot systems to realise a compact and nanofabrication-compatible architecture. Here we perform measurements of state-conditional coherent oscillations of a charge qubit. Using a quadruple quantum dot formed in a Si/SiGe heterostructure, we show the first demonstration of coherent two-axis control of a double quantum dot charge qubit in undoped Si/SiGe, performing Larmor and Ramsey oscillation measurements. We extract the strength of the capacitive coupling between a pair of double quantum dots by measuring the detuning energy shift (≈75 μeV) of one double dot depending on the excess charge configuration of the other double dot. We further demonstrate that the strong capacitive coupling allows fast, state-conditional Landau–Zener–Stückelberg oscillations with a conditional π phase flip time of about 80 ps, showing a promising pathway towards multi-qubit entanglement and control in semiconductor quantum dots.

Introduction

Since being proposed theoretically,^1,2 much experimental and theoretical progress has been made towards the development of a scalable quantum-computing architecture using electrically gated semiconductor quantum dot-based spin qubits.^3–23 Two-qubit Two-qubit gates are essential, and capacitive coupling has been used in GaAs quantum dot-based spin qubits to demonstrate both conditional singlet–triplet exchange oscillations,²⁴ and the generation of the entanglement of two neighbouring singlet–triplet qubits.²⁵ Recently, one- and two-qubit gate operations have been demonstrated in ²⁸Si-based quantum dot spin qubits,^26,27 harnessing the substantial improvement in coherence time achievable through isotopic purification and the corresponding reduction in nuclear spin density. Improving gate speeds provides an alternative route to realise high fidelity single- and multi-qubit gates, and intensive efforts have been made to realise fast manipulation of semiconductor spin qubits by mixing the spin degrees of freedom with charge degrees of freedom through spin–orbit coupling or the introduction of micromagnets.^28–30

Motivated by the search for high-speed qubits with strong interactions, semiconductor quantum dot charge qubits also have been studied and qubit manipulations performed in both GaAs^31–34 and Si,^35,36 with typical charge qubit coherence times of the order of 100 ps to 10 ns. Strong capacitive coupling between double dots is essential for two-qubit gates, and measured interdot capacitive couplings in GaAs quantum dots are in the range 25–120 μeV.^37–39 This capacitive coupling has been used to perform conditional rotations of a GaAs charge qubit;³⁸ yet similar measurements so far have not been possible in silicon-based quantum dots. Moreover, dopant-free devices, which have recently become prevalent for Si/SiGe quantum dot qubits, require a blanketing array of metal electrodes that partially screen the capacitive coupling, making this issue all the more urgent.^{12,17,30,40–43}

Here we present measurements of a quadruple quantum dot formed in an undoped Si/SiGe heterostructure and demonstrate fast and charge-state-conditional coherent manipulation of two strongly coupled double quantum dots. Non-adiabatic pulsed gate techniques allow fast two-axis control of the double dot charge qubit formed. We show that the strong capacitive coupling (>18 GHz) between two sets of double quantum dots enables charge-state-conditional coherent Landau–Zener–Stückelberg (LZS) interference with a conditional π phase flip time of approximately 80 ps, demonstrating progress towards realizing high-fidelity two-qubit control. Although we focus here on conditional coherent operations of a charge qubit, the measurement strategy and strong inter-qubit coupling deduced from the present study can also be directly applied to singlet–triplet²⁵ or hybrid quantum dot qubits,^18,20 where strong capacitive coupling will have an essential role in the realisation of fast two-qubit gates.

Results

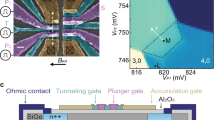
We study a linear quadruple quantum dot formed in an undoped Si/SiGe heterostructure, as shown in Figure 1a. The dots are formed under the gates D₁ through D₄, approximately under the dashed line shown in Figure 1a, and for the experiments we report here, it is useful to describe the quadruple quantum dot as a pair of double quantum dots. The right double dot (RDD), formed under the gates D₃ and D₄, forms a charge qubit that will be manipulated coherently based on the charge state of the left double dot (LDD), which is formed under gates D₁ and D₂. Charge sensing is performed by two charge-sensing quantum dots adjacent to the left (LSD) and right (RSD) hand sides of the quadruple dot array. The location of sensor RSD is close to the position that would naively be expected by examination of Figure 1a; to improve its charge sensitivity, sensor LSD is shifted to a position very close to the quadruple dot by careful tuning of the large number of gate voltages available on that side of the device. We monitor changes in the conductances g_L and g_R of sensor dots LSD and RSD, respectively, to monitor the electron occupations of double dots LDD and RDD. Figure 1c,d shows charge stability diagrams for the LDD (Figure 1c) and RDD (Figure 1d), respectively, demonstrating control of the four dot occupations as a function of the four gate voltages V_D1, V_D2, V_D3 and V_D4. As we show in Supplementary Figure S1e, the tunnel coupling and the capacitive coupling between the LDD and RDD both are reduced when the LDD has lower electron occupation. Thus, we perform here coherent manipulation in the regime for which the LDD has a total electron occupation larger than (10,10).

Figure 1

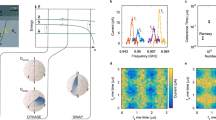
Si/SiGe device structure and charge stability diagrams of a pair of double quantum dots. (a) Scanning electron microscope image and schematic labelling of a device lithographically identical to the one used in the experiment. For clarity, only the gates in the bottom level are shown in the main panel. The inset to a shows the completed device with top level gates. Conductances through the left and right sensor dots (LSD and RSD) were used to monitor the charge occupations in the left and right double dots. (b) Schematic cross section through the dashed line in a and diagram of a pair of double quantum dots formed under gates D₁ to D₄. (c and d) Charge stability diagrams of the left (c) and right (d) double dots, measured using the conductance of LSD (g_L) and RSD (g_R), respectively. For clarity, a linear background was subtracted from the raw data, and the resulting conductance variations (Δg_L and Δg_R) are plotted.

We first show coherent two-axis control of an undoped Si/SiGe double dot charge qubit formed in the RDD. For this demonstration, the LDD energy detuning ε_L is kept >300 μeV so that the LDD charge occupation is not affected by the RDD manipulation pulses. The charge qubit states are defined as |0〉_R=|L〉 (excess charge is on the left dot) and |1〉_R=|R〉 (excess charge is on the right dot). The initial qubit state |0〉_R is prepared at negative RDD energy detuning ε_R. As shown schematically in Figure 2a–c, non-adiabatic control of the charge qubit is performed using abrupt changes in detuning energy with precise control of the pulse duration time as well as the amplitude. The pulses, generated using a Tektronix AWG70002A arbitrary waveform generator (AWG) with a rise time of 40 ps, are applied to gate D₃ through a commercial bias tee (Picosecond PulseLabs 5542–219). X-rotations on the Bloch sphere, shown in Figure 2a, correspond to oscillations between the qubit states |0〉_R and |1〉_R. Changing the peak detuning (ε_P) abruptly to ε_P=0, as shown by the green pulse in Figure 2b, yields in the ideal case an X-rotation on the Bloch sphere. At ε=0 the Hamiltonian is H=Δ_Rσ_x, where Δ_R is the tunnel coupling between D₃ and D₄, so the state evolves periodically in time at the Larmor frequency 2Δ_R/h, where h is Planck’s constant. In the experiment, there is a finite rise time for the pulse at the sample, and the axis of rotation on the Bloch sphere will depend on the exact detuning value reached at each stage of the pulse, so that the schematic drawings in Figure 2a,c are simpler than the case realized in the experiment. After a time evolution of duration t_p, the final state is measured by abruptly changing the detuning back to negative ε_R. We use the difference of the conductance of the RSD between |0〉_R and |1〉_R to determine a time-averaged signal proportional to the probability P₁ of the state being in |1〉_R.¹⁸

Figure 2

Demonstration of two-axis control of an undoped Si/SiGe charge qubit formed in the right double dot. (a) Time evolution of the Bloch vector during a non-adiabatic DC-pulsed gate (Larmor oscillation). An abrupt change in the detuning ε_R from a negative value, where state |0〉_R is the eigenstate of the Hamiltonian, to ε_P=0 induces a rotation of the state around the X-axis of the Bloch sphere. (b) Schematic energy level diagram of a double dot charge qubit with the pulse sequences for Larmor (X-axis rotation, green) and Ramsey (Z-axis rotation, orange) oscillation measurements. (c) Schematic time evolution of the Bloch vector during a Ramsey fringe measurement pulse sequence. An X_3π/2 pulse is applied to initialise the state on the XY plane of the Bloch sphere, and the state then evolves freely around the Z-axis for evolution time t_e with the rotation frequency E_01,R/h determined by the right qubit energy spliting E_01,R=$\sqrt{{{\epsilon }_{\mathrm{R}}}^2+{\left(2{\mathrm{\Delta }}_{\mathrm{R}}\right)}^2}$, where ${\epsilon }_{\mathrm{R}}$ and Δ_R are defined in the energy level diagram. A second X_3π/2 pulse maps the Y-axis to the (negative) Z-axis, and the average charge occupation is measured via the conductance change of the RSD (Figure 1a) (d) Coherent oscillation of uncalibrated probability P₁ in arbitrary units corresponding to Larmor oscillations (X-axis rotations) as a function of voltage V_D3 on gate D₃ and pulse duration t_p of a single-step pulse (see a, green pulse). (e) Line cut along the contour shown as the white dashed line in (d), which corresponds to ε_R=0, showing coherent Larmor oscillations. (f) Demonstration of Z-axis control performed with a Ramsey fringe experiment (corresponding to the orange pulse sequence shown in b): uncalibrated P₁ as a function of V_D3 and t_e. (g) Line cut through the Ramsey fringe data, taken at the value of V_D3 indicated by a red arrow in f, as a function of t_e. For clarity, a background probability variation of a third-order polynomial in time was removed from the raw P₁, as shown in the Supplementary Figure S3. The oscillations arise because of rotations of the Bloch vector about the Z-axis of the Bloch sphere. (h) Landau–Zener–Stüeckelburg (LZS) oscillation frequency f_LZS as a function of V_D3 in the regime, where the pulse maximum level detuning ε_p>Δ_R. The red solid line shows a linear fit to $\mathrm{\Delta }{f}_{\mathrm{LZS}}\approx {\alpha }_{{\epsilon }_{\mathrm{R},\mathrm{D}3}}\mathrm{\Delta }{V}_{\mathrm{D}3}$ with best fit parameter of gate D₃ lever arm ${\alpha }_{{\epsilon }_{\mathrm{R},\mathrm{D}3}}$≈32.5 GHz/mV≈135 μeV/mV.

Figure 2d,e shows coherent oscillations of P₁ resulting from the non-adiabatic Larmor pulse sequences described above. In Figure 2d, we plot P₁ as a function of t_p and the gate voltage V_D3, the latter of which determines the base level of ε_R. In order to overcome a sampling time limitation of our AWG, we modified the pulse generation scheme to allow sub-picosecond timing resolution (see Supplementary Figure S2). In Figure 2d, the path of the pulse maximum level detuning ε_P=0 is curved (see the white dashed curve following the maxima in Figure 2d, which is drawn by running a smooth curve through the oscillation peaks), most likely because of the finite rise time of the pulse and frequency-dependent attenuation in the microwave coaxial cable.³² Figure 2e shows a line cut through this path corresponding approximately to ε_P=0, revealing periodic oscillations in P₁ at a frequency of order 10 GHz, corresponding to Δ_R/h≃5 GHz. We typically observe beating of the oscillations after t_p=300 ps. This likely arises because of the superposition of a reflected part of the pulse with the original pulse, modifying the detuning amplitude.^18,32

The high-frequency oscillations of P₁ in Figure 2d for V_D3<222 meV arise from coherent LZS interference patterns.^44,45 As V_D3 becomes less positive in Figure 2d, the pulse maximum level detuning enters the regime ε_P>0, where the interdot tunnel coupling acts as a beam splitter.^46,47 Here the splitting ratio between the upper and lower branches of the charge qubit dispersion is determined by the detuning ramp rate in comparison with the tunnel coupling. On the return edge of the pulse, the two different trajectories returning through the beamsplitter at ε_P=0 can coherently interfere.

The measurement of qubit state rotations about the Z-axis on the Bloch sphere, shown schematically in Figure 2c, can be performed using two X_3π/2 pulses. The qubit state is first prepared in the state |−Y〉_R=$\sqrt{1/2}$(|0〉_R−i|1〉_R), by initialising to state |0〉_R and by performing an X_3π/2 rotation. The qubit state then acquires a relative phase $\mathit{\phi }=e^{-i{t}_{\mathrm{e}}\mathrm{\Delta }{E}_{01,\mathrm{R}}/h}$, where t_e is the time spent between the two X rotations at the base value of the detuning and the qubit energy splitting $E_{01,\mathrm{R}}=\sqrt{{{\epsilon }_{\mathrm{R}}}^2+{\left(2{\mathrm{\Delta }}_{\mathrm{R}}\right)}^2}$. This phase evolution corresponds to a rotation of the qubit state around the Z-axis of the Bloch sphere. Figure 2f,g shows the resulting quantum oscillations of the qubit state around the Z-axis of the Bloch sphere. In Figure 2g, the line cut is taken at V_D3∼222.7 mV in Figure 2f, corresponding to ε_P≈0, and a smooth third-order polynomial background oscillation was removed from the raw data for clarity^33,35 (Supplementary Figure S3). By fitting the data to an exponentially damped sinusoidal oscillation, we extract the Ramsey fringe oscillation frequency f_Ramsey ≈56 GHz and a coherence time $T_2^{*}$~51 ps.

The gate voltage dependence of both the LZS interference and the Ramsey fringe frequencies provides accurate measures of the detuning lever arm. Figure 2h shows the LZS oscillation frequency f_LZS as a function of V_D3. As these LZS oscillations are measured in the limit ε_P>Δ_R, we use an approximate form of the charge qubit energy level, $E_{01,\mathrm{R}}=\sqrt{{\epsilon }_{\mathrm{R}}^2+{\left(2{\mathrm{\Delta }}_{\mathrm{R}}\right)}^2}\approx {\epsilon }_{\mathrm{R}}=h{f}_{\mathrm{LZS}}$, and fit the data to the form $\mathrm{\Delta }{f}_{\mathrm{LZS}}={\alpha }_{{\epsilon }_{\mathrm{R},\mathrm{D}3}}\mathrm{\Delta }{V}_{\mathrm{D}3}$ to determine the gate lever arm ${\alpha }_{{\epsilon }_{\mathrm{R},\mathrm{D}3}}$≈32.5 GHz/mV≈135 μeV/mV.

We now discuss the measurement of the capacitive coupling between the double quantum dots. With the detuning lever arm calibrated as described above, the coupling strength can be measured by sweeping ε_L and ε_R through the LDD and RDD charge degeneracy points. Figure 3 shows the LDD and RDD polarisation lines, characterised by measuring the differential conductance of the left and right sensors, LSD (Figure 3a) and RSD (Figure 3b), as functions of the two critical variables, the detuning parameters for the LDD and RDD: ε_L and ε_R. We sweep ε_L and ε_R by controlling the voltages on (V_D1, V_D2) and (V_D3, V_D4), respectively. The positions of the excess charges (the electrons in each double dot that are free to move) are shown schematically as insets to Figure 3b. The coupled charge stability diagram reveals the four possible ground-state charge configurations for an extra electron in each of the two double dots. The grey dashed lines in Figure 3b show the RDD detuning energy shift (Δε_R) arising from the movement of a single electron from left to right in the LDD. The shift in this line is a direct measure of the energy shift in the RDD resulting from the capacitive coupling between the two double dots. From the energy calibrations reported above, we extract Δε_R≈75 μeV≈18.3 GHz. This energy shift is the available detuning modulation for the performance of two-qubit gates in quantum dots of a size and separation similar to those studied here.

Figure 3

Measurement of the capacitive coupling between two sets of double quantum dots. (a, b) The left and right double dot polarization lines are characterised by measuring the LSD (a) and RSD (b) differential conductances as functions of the detunings ε_L and ε_R. A polarisation line is identified by its large differential conductance. In b, the insets show schematic diagrams of the location of the excess charge in the capacitively coupled double quantum dots. The grey dashed lines represent the shift of RDD polarisation line detuning (Δε_R≈75 μeV) due to one electron moving from the left dot to the right dot in the LDD.

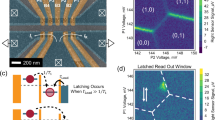
We now show that the capacitive coupling demonstrated above enables fast charge-state-conditional phase evolution of a quantum dot charge qubit. We study LZS oscillations in the RDD in the presence of a slowly varying perturbation from the excess charge in the LDD. Figure 4a illustrates schematically in green the pulse applied to the RDD for this experiment. The pulse is applied at a series of different values of ε_L (the vertical axis in Figure 4b–f). The pulse minimum detuning is controlled using V_D3, and the pulse amplitude is held fixed at 210 μeV. In Figure 4b–f, we vary V_D3 from 221.7 to 222.5 in steps of 0.2 mV. The effect of these steps is to change the energy in detuning of the maximum of the fast pulse, thus changing the frequency of the LZS oscillations. For example, the oscillations in Figure 4a are much faster than those visible in Figure 4f. The physical origin of this variation is the energy difference between the two charge qubit states: in Figure 4a, the maximum of the pulse sits at large detunings, corresponding to a large energy difference between the states. In contrast, in Figure 4f, the pulse maximum sits at detunings much closer to the charge qubit anticrossing, so that the energy difference between the charge qubit states is significantly smaller.

Figure 4

Charge-state-conditional coherent quantum interference. (a) Schematic diagram of the pulse sequence used for the measurement of Landau–Zener–Stückelberg (LZS) quantum interference in the right double dot (RDD) as a function of the detuning of the left double dot (LDD). (b–f) Coherent LZS oscillations of uncalibrated P₁ as a function of the LDD detuning ε_L and the duration t_p of the pulse applied to the RDD with fixed base levels of V_D3=221.7 (b), 221.9 (c), 222.1 (d), 222.3 (e) and 222.5 mV (f). (g) LZS interference frequencies, f_LZS, with (0, 1)_L—(black) and (1,0)_L—(red) excess charge configuration of the LDD as functions of V_D3. The black arrow in (e) highlights the shift in the location of the peak in the probability that corresponds to a conditional π phase rotation achieved in ∼80 ps.

For each of these LZS oscillation measurements, ε_L is slowly swept from +180 to −320 μeV (see the vertical axis in the top panels of Figure 4b–f). This variation in ε_L has two effects. First, the cross-talk between ε_L and the RDD results in a continuous shift in the detuning of the RDD, causing the LZS oscillations be tilted in each of the top panels of Figure 4b–f. Second (and this is the main result of Figure 4), at ε_L=0, the excess charge occupation of the LDD changes from (0, 1)_L to (1, 0)_L—this change occurs quite abruptly at zero detuning of the LDD, as can be observed in Figure 4b–f. This change in the charge configuration of the LDD produces a sudden decrease in frequency in Figures 4b–f at ε_L=0. This decrease in frequency reflects the decreased detuning ε_P that the LZS pulse maximum reaches because of the effective change in the pulse minimum detuning energy.

The bottom panels of Figure 4b–f show line cuts of the LZS oscillations in the RDD for the (0, 1)_L LDD ground state (black arrow on the left in Figures 4b) and (1, 0)_L LDD ground state (red arrow on the left in Figure 4b). At any given evolution time t_p, a phase change is clearly visible, and this phase change arises from the shift of one electron in the LDD. Using this effect, a charge-state-conditional π phase flip can be achieved in a time t_p as short as 80 ps, as indicated by the black arrow in Figure 4e.

Figure 4g shows the difference in f_LZS between the cases when the LDD ground state is (0, 1) (black circles) and when this ground state is (1, 0) (red circles). The frequency differences vary from 7 to 10 GHz, and this plot can be used to infer the speed of a conditional phase (CPHASE) gate if full control over qubits in both the left and right double dots in a device like that shown here is realized in the future. We emphasise that the frequency changes observed here arise from competing effects: f_LZS of the RDD increases as we change a gate voltage to increase ε_L, whereas f_LZS decreases as we cross zero detuning in the LDD, resulting in the motion of a single electron charge. As we take line cuts at ε_L≈±80 μeV to clearly show LZS oscillations in the (0, 1)_L and (1, 0)_L ground states, we believe that using an LDD detuning pulse amplitude <160 μeV, when LDD coherent manipulation is realized, can lead to a faster conditional phase gate than that estimated here.

Discussion

Here we have demonstrated a strong capacitive coupling of ≈18 GHz between two double quantum dots in a linear quadruple dot array geometry, and this coupling enabled the observation of fast charge-state-conditional coherent oscillations with a conditional phase flip time of 80 ps. Coupling of this magnitude demonstrates a key physical interaction necessary for a two-qubit CPHASE gate. Moreover, because we measure single-qubit X (Larmor) and Z (Ramsey) rotations with rotation frequencies also on the order of 10 GHz, one can envision universal quantum logic gates in semiconductor charge qubits that are all fast. Although we use abrupt changes in the baseline detuning here, resonant microwave control is also plausible,³⁶ in which case a two-qubit controlled not gate (CNOT) could be implemented in analogy with ref. 27. We stress, however, that the full demonstration of two-qubit charge qubit gates remains as a challenge, as in this work coherent control of the LDD could not be achieved. A more compact gate geometry that enables greater tunability in the tunnel coupling, which could potentially be achieved using an overlapped Al/Al₂O₃ gate structure,^26,43 is a promising path towards achieving fully tunable tunnel couplings in both neighbouring double quantum dots. Finally, we note that the strong capacitive coupling observed here is also a valuable resource with the potential to enable two-qubit gates in multi-electron spin qubits, including singlet–triplet^6,25 and hybrid quantum dot qubits.^{18,20,48–50}

Materials and methods

Fabrication

The device heterostructure was grown using chemical vapour deposition on commercially available SiGe substrates with a 29% Ge composition. The chemical vapour deposition growth sequence from the starting substrate was deposition of a strain-matched SiGe buffer layer followed by deposition of a 12-nm-thick strained Si well. The well was capped by deposition of 50 nm of SiGe, followed by a few nanometres of sacrificial strained Si to cap the heterostructure.

Devices were fabricated using a combination of electron beam lithography and photolithography. The device nanostructure was fabricated in two layers starting on a 15 nm gate dielectric of Al₂O₃ deposited by atomic layer deposition. The first layer of control gates was patterned in two electron beam lithography/metallisation steps to improve the gate density, and the metal layers were Ti followed by Au. The second reservoir gate layer (see inset to Figure 1a) is isolated from the first with another 80 nm layer of Al₂O₃ grown via atomic layer deposition. The second gate layer was also metallised with Ti/Au. A third layer of Al₂O₃ was deposited over the second gate layer to protect the gates during subsequent fabrication steps. Ohmic contacts were fabricated using annealed P+ ion implants.

Measurement

The charge stability diagrams of the LDD and RDD are characterised by measuring the conductance changes through the left and right sensor dots (LSD and RSD, respectively, see Figure 1a) that are operated at a fixed voltage bias of 50 μV, and the currents are measured with two current preamplifiers (DL Instruments model 1211). Supplementary Figure S1 shows large-scale charge stability diagrams and the positions of charge transitions of the LDD and RDD in the electron occupation regime used in the present experiment. For the manipulation of the RDD charge qubit, fast voltage pulses with repetition rate of 25 MHz are generated using two outputs of a Tektronix AWG70002A arbitrary waveform generator, which are added to the dot-defining dc voltage through a bias tee (Picosecond Pulselabs 5542–219) before being applied to gate D₃. The conductance change through the RSD with and without the manipulation pulses, measured with a lock-in amplifier (EG&G model 7265), is used to determine the average charge occupation. For the measurement of changes in charge occupation probabilities resulting from fast manipulation pulses, we modulated the manipulation pulses with a low frequency (≈777 Hz) square wave envelope, similar to the technique used in previous studies.^36,48 We compare the measured signal level with the corresponding |0〉_R to |1〉_R charge transition signal level, calibrated by sweeping gate D₃ and applying a 777 Hz square pulse to gate D₃ with an amplitude same as that of the manipulation pulses.