Main

Degenerate states appear ubiquitously in many physical settings as a result of an underlying symmetry. Breaking this symmetry through an external perturbation can lead to a splitting in the eigenvalue domain—an effect that has been exploited in a wide range of detection systems. In Hermitian environments, such as those encountered in quantum mechanics, the induced shift or separation in the eigenspectrum is at most of the same order as the perturbation ϵ itself (with ). In optics, this type of response is typically manifested in the resonance frequencies via variations in the complex refractive index and has provided the basis for various sensing arrangements, including microcavity sensors19,20,21 and ring laser gyroscopes22. In recent years, there has been a growing realization that non-conservative systems that operate around their degeneracies or exceptional points can provide a new way of enhancing their sensitivity beyond what is possible in standard arrangements. In such non-Hermitian configurations, the eigenfrequency splitting Δω can be accentuated by orders of magnitude, because it follows an ϵ1/N-dependence, where N represents the order of the exceptional point. In general, the order N is determined by the number of eigenvalues that simultaneously coalesce at the exceptional point. What makes this class of singularity so reactive to small perturbations is the fact that, in addition to the eigenvalues, all of the corresponding eigenvectors also merge at the relevant point in parameter space. In essence, around exceptional points, the system behaves as if it suddenly loses its dimensionality, because the vector space becomes severely skewed. Given that Δω ~ ϵ1/N, it is clear that the sensitivity of the system will increase with the order of the exceptional point—a feature that is highly desirable in detection applications. During the past few years, second-order exceptional points have been investigated in various photonic structures, including lasers11,12,23, photonic crystals7, synthetic lattices24 and topological arrangements25. On the other hand, higher-order non-Hermitian singularities have been reported only in coupled acoustic cavities that involve loss26. Such higher-order bifurcations and the ensuing boosts in the sensitivity of optical resonant arrangements have yet to be observed.

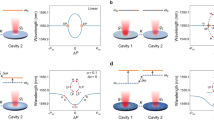
Of the many possible types of non-Hermitian photonic system, parity–time-symmetric arrangements are of particular interest because they provide an excellent platform for exploring the physics of exceptional points8,27. For instance, parity–time symmetry can be readily established in coupled resonators that simultaneously include gain and loss in a balanced fashion6,11, while allowing direct control over the energy exchange process through coupling. Figure 1a depicts two such parity–time-symmetric photonic molecules. The first involves two identical cavities, one experiencing gain and the other an equal amount of loss. The second consists of three resonators: the two from the first system separated by a neutral cavity. It can be shown that the former supports a second-order exceptional point, and the latter a third-order one. As a result, in the first case (N = 2), the eigenvalues are expected to diverge according to ϵ1/2, whereas for N = 3 the splitting would be more abrupt because it follows ϵ1/3. In principle, higher-order exceptional points can be synthesized in this manner by following a recursive bosonic quantization procedure28.

Figure 1: Parity–time-symmetric coupled cavity systems that support exceptional points.
figure 1

a, Schematics of binary (left) and ternary (right) parity–time-symmetric photonic molecules, with loss, gain and neutral resonators shown in blue, red and grey, respectively. Coupling between the resonators is represented by κ. b, A parity–time-symmetric ternary micro-ring system with equidistantly spaced cavities. The side resonators experience balanced gain and loss whereas the middle one is neutral. The rings (radius, 10 μm; width, 500 nm; height, 210 nm) consist of six quantum wells and are fabricated on an InP wafer. Three gold micro-heaters (thickness, approximately 150 nm) are fabricated underneath each cavity and are used to fine-tune the resonance wavelengths and to introduce thermal perturbations. The heating elements are shown in the inset. c, An SEM image of the structure at an intermediate fabrication step.

PowerPoint slide

Full size image

To demonstrate the enhanced sensitivity in a parity–time-symmetric ternary micro-ring laser system that supports a higher-order singularity (a third-order exceptional point), the active structure is implemented on an InP-based quantum well semiconductor wafer. The gain–neutral–loss profile is subsequently imposed by dynamically shaping the optical pump beam. In all cases, the resonance frequencies are fine-tuned using micro-heaters. By doing so, we can independently control the real and imaginary components of the refractive-index distribution, which is essential for establishing higher-order exceptional points. The resulting bifurcations in the frequency domain are monitored and characterized by allowing the system to operate in the lasing regime.

For the ternary parity–time-symmetric coupled micro-ring system (Fig. 1b), the two side ring resonators are subjected to equal amounts of gain and loss (g) while the middle ring remains neutral. In addition, the rings evenly exchange energy with each other with a coupling strength κ. A metallic (Au) heater is positioned under each cavity, with a vertical separation of approximately 3 μm. A scanning electron micrograph (SEM) image of the structure, at an intermediate stage of fabrication, is shown in Fig. 1c. The modal field evolution in this structure obeys idV/dt = H V, where V = (a, b, c)T represents the modal column vector, a, b and c represent field amplitudes in the amplifying, neutral and lossy cavities, respectively, and t represents time. H is the associated 3 × 3 non-Hermitian Hamiltonian:

in which +g (−g) accounts for the gain (loss). Without loss of generality, here the external perturbation ϵ is imposed on the cavity with gain; however it could be introduced anywhere along the diagonal of the matrix or to any of the coupling terms.

In the absence of any disturbance (ϵ = 0), assuming a harmonic dependence of V of the form , we can determine the complex eigenfrequencies ωn, (n ∈ {−1, 0, 1}) of the ternary system directly by solving the cubic algebraic equation

This equation indicates that when the gain/loss contrast reaches a critical value (in this case, ), all three eigenfrequencies coalesce at ωn = 0 and the system exhibits a third-order exceptional point. Moreover, at this specific point, the three eigenvectors of the ternary photonic molecule also coalesce, at , where A0 is a normalization constant, indicating that the energy in the central (neutral) cavity is twice that circulating in the other two resonators (which are subject to gain and loss).

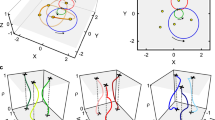
To understand how a small detuning or variation in the gain cavity affects the arrangement, we assume a small value for ϵ. In this case, the three complex eigenfrequencies of the configuration are obtained by numerically solving the characteristic cubic equation associated with the Hamiltonian in equation (1) (see Fig. 2a, b). Of particular interest is how this system reacts around the third-order exceptional point, when . The response is highlighted in the two cross-sections (in both the real and imaginary domains) in Fig. 2a, b, and in Fig. 2c, d (solid curves). The difference between two eigenfrequencies (in this case, ω0 and ω1) is also plotted (Fig. 2e, solid curve) as a function of ϵ. By considering the logarithmic behaviour of this curve (see Fig. 2f, solid line), we find that the slope of the response is 1/3, thus confirming that perturbations around a third-order exceptional point experience an enhancement of the form ϵ1/3.

Figure 2: Bifurcations of complex eigenfrequencies around a third-order exceptional point.
figure 2

a, The real parts of the eigenfrequencies (Re(ωn)) of the ternary parity–time-symmetric system as a function of the normalized gain/loss contrast g/κ and the detuning ϵ/κ. The third-order exceptional point (EP3) occurs at (blue plane) and ϵ = 0. b, The imaginary parts of the eigenfrequencies (Im(ωn)). c, d, Analytical (dashed lines) and numerical (solid lines) solutions for the real (c) and imaginary (d) parts of the eigenfrequencies, for . e, Analytical (dashed red line) and numerical (solid green line) results for Re(ω0 − ω1)/κ = Δω/κ, demonstrating cube-root behaviour as a function of the detuning. f, The results from e on a logarithmic scale. The slope of 1/3 confirms the cube-root response.

PowerPoint slide

Full size image

Alternatively, we can explain this behaviour using perturbation theory. Around the third-order exceptional point, the characteristic equation is

The roots of this cubic equation can be self-consistently obtained by assuming that , contrary to what might be expected in Hermitian settings, in which the perturbative series proceeds in integer powers of ϵ. From these expressions, we find that

with n ∈ {−1, 0, 1}. The response of the system based on this expression (Fig. 2c–f, dashed curves) is in close agreement to that obtained numerically. Our analysis indicates that the real parts of ω0 and ω1 diverge from each other in an ϵ1/3 fashion. (More details about the eigenvalue spectrum of these systems is provided in Methods section ‘Coupled mode analysis of the ternary system’.) Consequently, the sensitivity of the ternary system can be assessed by monitoring the separation of the ω0 and ω1 spectral lines, which is expected to approximately follow

The micro-ring resonators used in this study have radii of 10 μm (with a free spectral range of approximately 10 nm), widths of 500 nm and heights of 210 nm. The cross-section of each ring is designed to ensure single transverse mode conditions at the wavelength of operation λ0 ≈ 1,600 nm. The system was implemented using InGaAsP quantum wells to provide the necessary modal gain, which is estimated to be about 100 cm−1. Given that the optical group index in these nano-waveguides is approximately 4 around the operating wavelength, g ≈ 1012 s−1. The coupling coefficients κ reach similar levels when varying the distance between neighbouring rings. Details about the fabrication procedure of these structures are provided in Methods section ‘Fabrication’.

In our experiments, the imaginary components of the refractive index in the different regions of the structure are engineered by spatially shaping the pump beam at 1,064 nm (see Methods section ‘Measurement set-up’). The real part of the refractive index is fine-tuned using micro-heaters to ensure that the cavities are phase-matched. Both of these procedures are necessary to bring the coupled micro-ring lasers into the exceptional-point regime. Once the configuration is set to operate at such a state, the gain cavity is perturbed by supplying current I into the corresponding heater. By doing so, the change in the refractive index is varied linearly with the electrical power that is dissipated in the resistor (ϵ ∝ I2). As a result, the lasing frequencies begin to diverge and the ensuing splitting as a function of ϵ is monitored. The relationship between the induced differential detuning and the power of the heaters is experimentally characterized by intentionally decoupling the micro-rings (see Methods section ‘Characterization of thermally applied perturbations’).

Before carrying out experiments in the more involved ternary system, we first characterize the bifurcation behaviour of a second-order exceptional point associated with a parity–time-symmetric coupled micro-ring structure (Fig. 1a, left). As shown in Methods section ‘Coupled mode analysis of the binary system’, once a small frequency mismatch ϵ is thermally introduced to the optical oscillator around the second-order exceptional point, the two lasing frequencies split according to . The coupling factor in this binary arrangement is measured to be about 1012 s−1 when the rings are separated29 by 100 nm. Figure 3a clearly demonstrates a square-root wavelength splitting in response to changes in the power dissipated in the heater, in accordance with theoretical expectations. The observed linear slope of 1/2 in the corresponding logarithmic plot affirms this behaviour (Fig. 3a, inset). Figure 3b depicts the measured enhancement in sensitivity as a function of the induced perturbation (in terms of the shift in resonance frequency). In our study, the enhancement is defined in terms of experimentally accessible quantities (ΔωEP2/ϵ ∝ (κ/ϵ)1/2). Because of the presence of an exceptional point, the enhancement factor increases for small values of ϵ. In this case, we observed an enhancement of up to 13 times in the detuning range below 10 GHz (see Methods section ‘Role of coupling in sensitivity enhancement’ for more details).

Figure 3: Binary parity–time-symmetric system operating around a second-order exceptional point.
figure 3

a, Observed frequency splitting as a function of the power that is dissipated in the heaters (ϵ ∝ I2). The perturbation is imposed on the active cavity. The inset demonstrates a slope of 1/2 on a logarithmic scale, confirming the existence of a second-order exceptional point. The solid lines are the simulated square-root behaviour, the filled circles indicate experimental data, and the error bars indicate the uncertainty in frequency measurements due to the spectrometer. b, Measured enhancement factor as a function of the induced perturbation. For a detuning of less than 10 GHz, an enhancement of about 13 times is observed. The enhancement is defined in terms of experimentally accessible quantities (ΔωEP2/ϵ, where ϵ is the measured detuning for an isolated cavity at similar heater power). The solid line shows the curve ΔωEP2/ϵ ∝ (κ/ϵ)1/2 and squares depict experimental data. The inset shows the perturbation as a function of the dissipated power, where the solid line is a linear fit to the measured values (circles).

PowerPoint slide

Full size image

We next investigate the sensitivity of a ternary parity–time-symmetric system when operating close to a third-order exceptional point. The structure consists of three equidistantly spaced micro-rings, with a coupling strength of approximately 9 × 1011 s−1 when separated by 150 nm. To establish parity–time symmetry in the system, the pump beam is completely withheld from one of the side rings using a knife edge. In addition, the central (neutral) ring is partially illuminated while the third ring is fully pumped. By adjusting the position of the knife edge and the pump level, the three lasing modes of the structure gradually coalesce into one line (approximately 1,602 nm), which is associated with the emergence of a third-order exceptional point. The intensity profile (Fig. 4a) of the lasing mode at this point is captured using a charge-coupled device (CCD) camera and is found to be in agreement with that expected from theory. Integrating the intensity over the captured image reveals a distribution of (1, 1.95, 1.16); that is, the intensity in the neutral element is almost twice that in the others. Once the system reaches the regime in which the third-order exceptional point exists, the heater underneath the pumped cavity is activated. As a consequence of this perturbation, the single lasing mode splits into three distinct branches, as anticipated from theory (Fig. 2c). The spectral evolution of this transition is collected using a spectrometer with an array detector (Fig. 4b). We note that the spectral power and linewidth of each eigenvector are associated with the imaginary part of the corresponding eigenfrequency. In this regard, Fig. 4b indicates that the eigenfrequency with the largest real part (longest wavelength) is the one that exhibits the highest gain, as theoretically expected from Fig. 2c, d. Moreover, Fig. 4b confirms that the laser linewidth is enhanced when the system operates in the parameter regime that corresponds to a third-order exceptional point, as is known to be the case, owing to the so-called Petermann factors30. As previously indicated, in this experiment we monitor the difference between the resonance frequencies ω0 and ω1. Figure 4c verifies that the frequency separation ΔωEP3 exhibits cube-root behaviour as a function of ϵ; this is also confirmed by plotting these data on a logarithmic scale, from which we directly infer a slope of 1/3 (Fig. 4c, inset). The sensitivity enhancement factor (ΔωEP3/ϵ ∝ (κ/ϵ)2/3) corresponding to the ternary photonic molecule is plotted in Fig. 4d. In this case, the sensitivity is magnified approximately 23 times when the detuning between the active and neutral resonators is below 5 GHz. Further discussion about the practical aspects of sensitivity enhancement are provided in Methods section ‘Further discussion’.

Figure 4: Response of a ternary parity–time-symmetric system biased at a third-order exceptional point.
figure 4

a, Intensity profile (colour scale) of the lasing mode in a ternary parity–time-symmetric arrangement at a third-order exceptional point. The energy in the central cavity is approximately twice that in the side resonators, because the eigenvector is given by . b, Spectra of the three lasing modes (identified by the three peaks) as the system departs from the exceptional point with increasing I2 ∝ ϵ. c, The splitting between two neighbouring lasing lines as a function of I2. Inset shows a line with a slope of 1/3 on a logarithmic scale. The solid lines are the simulated cube-root behaviour, the filled circles denote experimental data, and the error bars indicate the uncertainty in frequency measurements due to the spectrometer. d, The measured sensitivity enhancement is about 23 times for detunings of less than 10 GHz. The solid line shows the curve ΔωEP3/ϵ ∝ (κ/ϵ)2/3 and squares indicate measured values. Inset, the perturbation as a function of I2, where circles denote experimental data and the solid line is a linear fit.

PowerPoint slide

Full size image

In conclusion, we have presented an experimental demonstration of higher-order exceptional points in an optical parity–time-symmetric coupled micro-resonator system. The response of the ternary lasing molecule exhibits cube-root behaviour, which could be used to improve the sensing performance of micro-resonator arrangements. Our approach can in principle be adopted in various other photonic configurations. Furthermore, the properties associated with these higher-order degeneracies can be exploited in fields other than optics, by introducing non-Hermiticity to enhance sensing capabilities. Our results may pave the way towards a new class of on-chip ultrasensitive sensing system.

Methods

Coupled mode analysis of the ternary system

In this section, we provide an analytical approach to studying the evolution of eigenfrequencies of a ternary parity–time-symmetric photonic molecule around an exceptional point. In such configurations, one resonator (with modal field a) is subjected to a gain g, the central cavity (with modal field b) is kept neutral and the third resonator (with modal field c) experiences an amount of loss −g equal to the gain of the first resonator. In the time domain, and considering sinusoidally time varying fields , the modal amplitudes a, b and c obey the coupled differential equations

where κ denotes the coupling strength between adjacent cavities. To determine the eigenvalues of this system, we use the representation , which leads to an eigenvalue equation of the form H0Vn = ωnVn, where the Hamiltonian H0 is

For non-trivial solutions (det(H0 − ωnI) = 0, where I is the identity matrix), we obtain the characteristic equation

which results in the following three eigenvalues:

For , all three eigenvalues are real. In this case, the system is considered to be in a regime in which parity–time symmetry is not broken. For  , two of the three eigenvalues become purely imaginary, resulting in a situation in which parity–time symmetry is broken. At , as the system transitions from the unbroken to the broken regime, all three eigenvalues and their corresponding eigenvectors coalesce. This juncture at which the dimensionality of the system abruptly changes from three to one is known as a third-order exceptional point. At this point, the eigenvalues are all equal (ωn = 0), and their associated eigenvectors are

To study the bifurcation properties of the eigenvalues, it is convenient to introduce a normalized parameter . The perturbed Hamiltonian H can then be written as

where, ϵ1, ϵ2 and ϵ3 represent the perturbations induced on gain, neutral and loss cavities, respectively. For the cases we study here, we assume that the perturbations negligibly affect the coupling. As a result, the perturbation terms (ϵ1, ϵ2 and ϵ3) appear only along the diagonal elements of H. The determinant of H equated to zero is

where . For a system that is biased at the exceptional point (), the associated characteristic equation is

Because , higher-order terms can be ignored and the above simplifies to

Here, three different scenarios are investigated, in which the perturbation is on (i) the gain element, (ii) the neutral element and (iii) the gain and neutral elements. The third scenario is the most relevant to our experiment, in which a heater located underneath the gain cavity introduces the perturbation, because the generated heat perturbs the neutral cavity as well, owing to thermal diffusion.

Perturbing the gain cavity only

In this case, ϵ1 = ϵ and ϵ2 = ϵ3 = 0 so equation (2) reduces to

This equation can be perturbatively expanded using a Newton–Puiseux series. Considering the first two terms only, , with the coefficients c1 and c2 being complex constants, results in

Forcing the coefficients of the first two terms to be zero, we obtain three sets of values for the coefficients c1 and c2, corresponding to the three eigenvalues:

The bifurcations in the eigenvalues now acquire the form

As equation (3) indicates, the frequency splitting between and and between and follow the cube-root of ϵ, whereas the difference between the real parts of and is of the order of ϵ2/3. This behaviour can be characterized experimentally in the spectral domain by monitoring the resonant frequency splitting of, for example, and . This splitting can be written as

In general, a detection target such as a nanoparticle or biological subject can alter not only the resonance frequency of the cavity sensor, but it also its Q-factor. In the proposed model, the applied perturbation ϵ can be complex, which accounts for the scattering loss induced by the target. In this regard, we write the perturbation as ϵ = ϵ0 + iβ ϵ0. However, small amounts of loss (for example, 0 < β < 1) introduced by a sensing subject do not have a large effect on the performance of the sensor that exhibits a third-order exceptional point.

Perturbing the neutral cavity only

For a perturbation of the neutral cavity, ϵ2 = ϵ and ϵ1 = ϵ3 = 0. As a result, the characteristic equation (equation (2)) can be written as

Again assuming a Newton–Puiseux perturbative expansion for , we obtain

The three sets of values for the coefficients c1 and c2 are

and the resulting bifurcations in the eigenvalues acquire the form

Perturbing the gain and neutral cavities

In this case, we assume the stronger perturbation is applied to the cavity with gain; therefore, ϵ1 = ϵ, ϵ2 = α ϵ (α < 1) and ϵ3 = 0. The characteristic equation, according to equation (2), is

After expanding the eigenvalues using , we obtain

By forcing the coefficients of the first two terms to be zero, we fine c1 and c2 to be

The bifurcations in the eigenvalues now acquire the form

The similarity between equations (4) and (3) demonstrates that the scenario in which the gain and neutral cavities are perturbed is very similar to that in which the perturbation affects the gain cavity only; the only differences are the (1 − 2α)1/3 coefficients. Therefore, the bifurcation characteristics in the latter scenario can to some extent be applied in the former scenario as well. For example, the frequency splitting between and follows the cube-root of the induced perturbation and can be written as

This equation indicates that the presence of ϵ2 reduces the sensitivity of the system by a factor of . Therefore, the sensitivity can be further improved when the outer cavities are fully isolated from the introduced perturbation.

Fabrication

Extended Data Fig. 1a shows the fabrication steps involved in the preparation of the coupled micro-ring structures used in this study. The multiple-quantum-well gain system consists of six Inx=0.734Ga1−xAsy=0.57P1−y wells (thickness, 10 nm), each sandwiched between two cladding layers of Inx=0.56Ga1−xAsy=0.938P1−y (thickness, 20 nm), all grown on a p-type InP substrate. The quantum wells are covered by a 10-nm-thick InP protective layer. The epitaxially grown wafer, using metalorganic chemical vapour deposition, was supplied by OEpic Semiconductors Inc.

To fabricate the micro-ring resonators, hydrogen silsesquioxane (HSQ) solution in methyl isobutyl ketone (MIBK) was first spin-coated on the wafer as a negative-tone inorganic electron beam resist; the wafer was then patterned using electron beam lithography. The structures were developed using tetramethylammonium hydroxide (TMAH) and subsequently transferred to the wafer through a reactive-ion-etching (RIE) process. The dry etching involves H2:CH4:Ar gases with flow rates of 40:4:20 standard cubic centimetres (sccm), a RIE power of 150 W and a chamber pressure of 30 mT. An SEM image of the sample at the end of this step is shown in Fig. 1b. Next, a 500-nm-thick silicon dioxide (SiO2) film is deposited on the structure using plasma-enhanced chemical vapour deposition (PECVD) to promote the adhesion of bisbenzocyclobutene (BCB). Subsequently, a 3-μm-thick layer of BCB was spin-coated on the sample and cured for planarization. The pattern of the heaters was then aligned on the top of the rings and projected onto a NR71000PY negative resist via photolithography. The pattern was developed in RD6 developer for 7 s. Next, we deposited 10 nm of titanium (for adhesion) and 150 nm of gold using thermal evaporation. The sample was then immersed in RR41 resist remover that was heated up to 100 °C to lift off the remaining photoresist. A microscope image of the sample at this stage (Extended Data Fig. 1b) shows the gold heaters that are fabricated at a vertical distance of 3 μm above the rings. This distance was chosen to eliminate the optical interaction between the cavity mode and the metallic section. The sample was then wire-bonded to a 16-pin carrier (TO8 header) to provide access to the heaters during the experiment (Extended Data Fig. 1c). Subsequently, the patterns were covered with SU8 photoresist for protection and to provide mechanical support. Finally, the InP substrate was removed by wet etching in hydrochloric acid (HCl). This wet etching process is highly selective and stops abruptly after removing the InP substrate, leaving the InGaAsP quantum wells intact. This process leaves the micro-rings partially embedded in the SiO2 matrix and exposed to air. Afterwards, the structure is accessible for the measurement from the backside through a hole drilled in the header (Extended Data Fig. 1d).

Measurement set-up

The micro-ring arrangements were optically pumped with a pulsed 1,064-nm laser (SPI fibre laser). A schematic of the measurement set-up is provided in Extended Data Fig. 2. The diameter of the beam was arranged such that at the surface of the sample it had a diameter of about 100 μm. A microscope objective with a numerical aperture of 0.42 was used to project the pump beam onto the rings and to collect the output light from the samples. Alignment of the pump beam to the desired cavity was performed by imaging the sample surface through two cascaded 4-f imaging systems onto an infrared CCD camera (Xenics Inc.), using a broadband infrared light source. Output spectra were obtained using a spectrometer (Horiba Scientific iHR320) equipped with a grating of 900 grooves per mm in conjunction with an electrically cooled InGaAs detector (Synapse EM). The spectrometer entrance slit was set to 100 μm to obtain the resolution of approximately 0.13 nm. To establish the parity–time symmetry in the structures, the micro-rings were pumped selectively by using a movable knife edge, imaged on the surface of the sample. The gain/loss distribution required was realized by adjusting the intensity of the pump beam and position of the knife edge. Extended Data Fig. 3 shows the intensity profile of the pump beam at the sample, with and without the image of the knife edge. The current to the heaters were supplied by precision current sources (ILX Lightwave) to ensure stability of the induced thermal perturbations. Extended Data Fig. 4a and b depicts the associated ring resonators when they are all evenly pumped, and the three heaters imaged on the measurement station using a broadband near-infrared source, respectively.

Characterization of thermally applied perturbations

This section provides some considerations regarding the experimental characterization of perturbations in the coupled micro-ring system. Generally, after reaching the exceptional point, the perturbation is applied through the micro-heater that is incorporated under the cavity with gain. However, owing to thermal diffusion, the power dissipated by this heater (P = RI2, with R the resistance) also affects the refractive index of other cavities, although to a lesser degree. One way to correctly factor in the effect of this heat diffusion is to intentionally decouple the micro-rings involved and then measure the resultant detuning in the resonance frequency (Δω) of the cavities as a function I2.

In the binary configuration (Extended Data Fig. 5a), the effective imposed perturbation is the difference between the shifts in the resonance frequencies of the two cavities, ϵ = Δω1 − Δω2, which is measured to be ϵ ≈ 1.17I2. In this case, the sensitivity enhancement (Fig. 3b) is defined as ΔωEP2/ϵ. Note that the relationship between the imposed detuning and the power of the heater is a function of various parameters in the system, such as ohmic resistance and the vertical separation of the heaters from the rings; hence it may vary from sample to sample. Consequently, the only way to reliably estimate the change in refractive index due to heat diffusion is to fully decouple the rings and measure it directly, as explained above.

For the ternary system (Extended Data Fig. 5b), the situation is yet more complicated because, in effect, two different perturbations are present. By changing the current of the heater, the perturbation will be applied not only to the cavity with gain but also to the other two cavities. In this respect, the most pronounced perturbation is between the gain and loss resonators (ϵ1 = Δω1 − Δω3). In addition, there is an inevitable perturbation between the neutral and loss cavities (ϵ2 = Δω2 − Δω3). In our system, these two values were measured to be ϵ1 = 1.4I2 and ϵ2 = 0.82I2. Following the approach in Methods section ‘Coupled mode analysis of the ternary system’, we write ϵ2 = α ϵ1, where α is measured to be 0.6. As discussed in Methods section ‘Coupled mode analysis of the ternary system’, the presence of ϵ2 in the system reduces the sensitivity by , which translates to a decrease in the ensuing frequency splitting and consequently the enhancement factor by a factor of two. For the ternary system, the sensitivity enhancement (Fig. 4d) is defined as ΔωEP3/(ϵ1 − ϵ2).

Coupled mode analysis of the binary system

A similar approach to that outlined in Methods section ‘Coupled mode analysis of the ternary system’ can be used to analyse a binary parity–time-symmetric photonic molecule. This system consists of two coupled cavities, one (a) that experiences a gain g and its counterpart (b), which is subjected to an equal amount of loss −g. The field evolution in this case is

Using the representation , this equation corresponds to the eigenvalue equation H0Vn = ωnVn. The matrix H0 is

Setting det(H0 − ωnI) = 0, where here I is the identity matrix, the corresponding characteristic equation and associated eigenfrequencies are

and

In this configuration, parity–time symmetry is unbroken under the condition g < κ, which implies that the two eigenvalues given by equation (5) are real. However, for g > κ, the two eigenvalues become imaginary and the system is said to have entered a broken-symmetry phase. At g = κ, the system is at its second-order exceptional point, at which the two eigenvalues coalesce (ω−1 = ω1 = 0). In addition, at this point the two eigenvectors are also identical:

The generalized perturbed Hamiltonian for this binary configuration can be written as

where the normalization is applied. Eigenvalues for H can therefore be found from the determinant

in which . The resulting characteristic equation is

Biasing the system around the exceptional point () transforms the characteristic equation to

Without loss of generality, we assume that the perturbation affects only the gain cavity (ϵ1 = ϵ, ϵ2 = 0). In this case, the characteristic equation above reduces to

In contrast to the analysis of third-order exceptional points, the Newton–Puiseux series that begins with a square-root element is required, because the exceptional point is of order two. Hence, the first two terms of this series can be written as

By inserting the above expansion into equation (6), we can determine the coefficients c1 and c2:

Setting the first two terms in this equation to zero leads to the following two sets of values:

The resulting eigenvalue bifurcations are

These expressions indicate that for a binary arrangement the real parts of the eigenfrequencies bifurcate with a square-root dependence on the applied perturbation ().

Role of coupling in sensitivity enhancement

For a two-ring system, the sensitivity enhancement follows the square-root of the coupling factor. The coupling strength can be determined experimentally by measuring the frequency splitting of the modes of a dimer laser directly when the two rings are equally pumped. Extended Data Fig. 6a shows how the coupling strength affects the perturbation-induced splitting. It is evident in Extended Data Fig. 6a that the sensitivity of the system is enhanced by increases in the coupling strength between the resonators. The same results are shown in a logarithmic scale in Extended Data Fig. 6b, and confirm the desired square-root behaviour (lines with a slope of 0.5).

Further discussion

In general, the gain threshold for lasing and the gain that is required to reach the exceptional point can be designed to be different. As long as the system is designed such that the gain required for exceptional point is larger than the gain threshold for each ring to lase, the system can be a laser at the exceptional point31,32.

As indicated in Methods section ‘Characterization of thermally applied perturbations’, the reported sensitivity response of the ternary system can be further boosted if the perturbation is applied on only one of the cavities. In our experiment, as a result of thermal diffusion, both (gain and neutral) resonators were differentially detuned and so the achievable enhancement was reduced by a factor of two. Finally, we note that in all of our measurements the observed maximum enhancement is limited by the detection limit that is imposed by the linewidth of our lasers, which can in principle be reduced either by switching to other gain systems or by using coherence-improving geometries33,34. The linewidth enhancement at the exceptional point, although still a subject of debate, is another important consideration in using these systems35,36. Such systems may find application in rotation sensing37.

Data availability

The datasets generated during and analysed during this study are available from the corresponding author on reasonable request.