Abstract
The whole frame of interconnections in complex networks hinges on a specific set of structural nodes, much smaller than the total size, which, if activated, would cause the spread of information to the whole network1, or, if immunized, would prevent the diffusion of a large scale epidemic2,3. Localizing this optimal, that is, minimal, set of structural nodes, called influencers, is one of the most important problems in network science4,5. Despite the vast use of heuristic strategies to identify influential spreaders6,7,8,9,10,11,12,13,14, the problem remains unsolved. Here we map the problem onto optimal percolation in random networks to identify the minimal set of influencers, which arises by minimizing the energy of a many-body system, where the form of the interactions is fixed by the non-backtracking matrix15 of the network. Big data analyses reveal that the set of optimal influencers is much smaller than the one predicted by previous heuristic centralities. Remarkably, a large number of previously neglected weakly connected nodes emerges among the optimal influencers. These are topologically tagged as low-degree nodes surrounded by hierarchical coronas of hubs, and are uncovered only through the optimal collective interplay of all the influencers in the network. The present theoretical framework may hold a larger degree of universality, being applicable to other hard optimization problems exhibiting a continuous transition from a known phase16.
Similar content being viewed by others
Main
The optimal influence problem was initially introduced in the context of viral marketing1, and its solution was shown to be NP-hard4 for a generic class of linear threshold models of information spreading17,18. Indeed, finding the optimal set of influencers is a many-body problem in which the topological interactions between them play a crucial role13,14. On the other hand, there has been an abundant production of heuristic rankings to identify influential nodes and ‘superspreaders’ in networks6,7,8,9,10,11,12,19. The main problem is that heuristic methods do not optimize a global function of influence. As a consequence, there is no guarantee of their performance.
Here we address the problem of quantifying nodes’ influence by finding the optimal (that is, minimal) set of structural influencers. After defining a unified mathematical framework for both immunization and spreading, we provide its optimal solution in random networks by mapping the problem onto optimal percolation. In addition, we present CI (Collective Influence), a scalable algorithm to solve the optimization problem in large-scale real data sets. The thorough comparison with competing methods (Supplementary Information section I20) ultimately establishes the better performance of our algorithm. By taking into account collective influence effects, our optimization theory identifies a new class of strategic influencers, called ‘weak nodes’, which outrank the hubs in the network. Thus, the top influencers are highly counterintuitive: low-degree nodes play a major broker role in the network, and despite being weakly connected, can be powerful influencers.
The problem of finding the minimal set of activated nodes17,18 to spread information to the whole network4 or to optimally immunize a network against epidemics11 can be exactly mapped onto optimal percolation (see Supplementary Information section IIB). This mapping provides the mathematical support to the intuitive relation between influence and the concept of cohesion of a network: the most influential nodes are the ones forming the minimal set that guarantees a global connection of the network5,9,10. We call this minimal set the ‘optimal influencers’ of the network. At a general level, the optimal influence problem can be stated as follows: find the minimal set of nodes which, if removed, would break down the network into many disconnected pieces. The natural measure of influence is, therefore, the size of the largest (giant) connected component as the influencers are removed from the network.
We consider a network composed of N nodes tied with M links with an arbitrary-degree distribution. Let us suppose we remove a certain fraction q of the total number of nodes. It is well known from percolation theory21 that, if we choose these nodes randomly, the network undergoes a structural collapse at a certain critical fraction where the probability of existence of the giant connected component vanishes, G = 0. The optimal influence problem corresponds to finding the minimum fraction qc of influencers to fragment the network: qc = min{q ∈ [0, 1]: G(q) = 0}.
Let the vector n = (n1,…, nN) represent which node is removed (ni = 0, influencer) or left (ni = 1, the rest) in the network ( ), and consider a link from i to j (i → j). The order parameter of the influence problem is the probability that i belongs to the giant component in a modified network where j is absent, νi→j (refs 22, 23). Clearly, in the absence of a giant component we find {νi→j = 0} for all i → j. The stability of the solution {νi→j = 0} is controlled by the largest eigenvalue λ(n; q) of the linear operator
), and consider a link from i to j (i → j). The order parameter of the influence problem is the probability that i belongs to the giant component in a modified network where j is absent, νi→j (refs 22, 23). Clearly, in the absence of a giant component we find {νi→j = 0} for all i → j. The stability of the solution {νi→j = 0} is controlled by the largest eigenvalue λ(n; q) of the linear operator  defined on the 2M × 2M directed edges as
defined on the 2M × 2M directed edges as  . We find for locally tree-like random graphs (see Fig. 1a and Supplementary Information section II):
. We find for locally tree-like random graphs (see Fig. 1a and Supplementary Information section II):

where  is the non-backtracking matrix of the network15,24. The matrix
is the non-backtracking matrix of the network15,24. The matrix  has non-zero entries only when (k → ℓ, i → j) form a pair of consecutive non-backtracking directed edges, that is, (k → ℓ, ℓ → j) with k ≠ j. In this case
has non-zero entries only when (k → ℓ, i → j) form a pair of consecutive non-backtracking directed edges, that is, (k → ℓ, ℓ → j) with k ≠ j. In this case  (equation (13) in Supplementary Information). Powers of the matrix
(equation (13) in Supplementary Information). Powers of the matrix  count the number of non-backtracking walks of a given length in the network (Fig. 1b)24, much in the same way as powers of the adjacency matrix count the number of paths5. Operator
count the number of non-backtracking walks of a given length in the network (Fig. 1b)24, much in the same way as powers of the adjacency matrix count the number of paths5. Operator  has recently received a lot of attention thanks to its high performance in the problem of community detection25,26. We show its topological power in the problem of optimal percolation.
has recently received a lot of attention thanks to its high performance in the problem of community detection25,26. We show its topological power in the problem of optimal percolation.
a, The largest eigenvalue λ of  exemplified on a simple network. The optimal strategy for immunization and spreading minimizes λ by removing the minimum number of nodes (optimal influencers) that destroys all the loops. Left panel, the action of the matrix
exemplified on a simple network. The optimal strategy for immunization and spreading minimizes λ by removing the minimum number of nodes (optimal influencers) that destroys all the loops. Left panel, the action of the matrix  is on the directed edges of the network. The entry
is on the directed edges of the network. The entry  encodes the occupancy (n3 = 1) or vacancy (n3 = 0) of node 3. In this particular case, the largest eigenvalue is λ = 1. Centre panel, non-optimal removal of a leaf, n4 = 0, which does not decrease λ. Right panel, optimal removal of a loop, n3 = 0, which decreases λ to zero. b, A NB walk is a random walk that is not allowed to return back along the edge that it just traversed. We show a NB open walk (ℓ = 3), a NB closed walk with a tail (ℓ = 4), and a NB closed walk with no tails (ℓ = 5). The NB walks are the building blocks of the diagrammatic expansion to calculate λ. c, Representation of the global minimum over n of the largest eigenvalue λ of
encodes the occupancy (n3 = 1) or vacancy (n3 = 0) of node 3. In this particular case, the largest eigenvalue is λ = 1. Centre panel, non-optimal removal of a leaf, n4 = 0, which does not decrease λ. Right panel, optimal removal of a loop, n3 = 0, which decreases λ to zero. b, A NB walk is a random walk that is not allowed to return back along the edge that it just traversed. We show a NB open walk (ℓ = 3), a NB closed walk with a tail (ℓ = 4), and a NB closed walk with no tails (ℓ = 5). The NB walks are the building blocks of the diagrammatic expansion to calculate λ. c, Representation of the global minimum over n of the largest eigenvalue λ of  versus q. When q ≥ qc, the minimum is at λ = 0. Then, G = 0 is stable (still, non-optimal configurations exist with λ > 1 for which G > 0). When q < qc, the minimum of the largest eigenvalue is always λ > 1, the solution G = 0 is unstable, and then G > 0. At the optimal percolation transition, the minimum is at n* with λ(n*, qc) = 1. For q = 0, we find λ = κ − 1 (κ = 〈k2〉/〈k〉, where k is the node degree) which is the largest eigenvalue of
versus q. When q ≥ qc, the minimum is at λ = 0. Then, G = 0 is stable (still, non-optimal configurations exist with λ > 1 for which G > 0). When q < qc, the minimum of the largest eigenvalue is always λ > 1, the solution G = 0 is unstable, and then G > 0. At the optimal percolation transition, the minimum is at n* with λ(n*, qc) = 1. For q = 0, we find λ = κ − 1 (κ = 〈k2〉/〈k〉, where k is the node degree) which is the largest eigenvalue of  for random networks25 with all nodes present (ni = 1). When λ = 1, the giant component is reduced to a tree plus one single loop (unicyclic graph), which is suddenly destroyed at the transition qc to become a tree, causing the abrupt fall of λ to zero. d, Ball(i, ℓ) of radius ℓ around node i is the set of nodes at distance ℓ from i, and ∂Ball is the set of nodes on the boundary. The shortest path from i to j is shown in red. e, Example of a weak node: a node with a small number of connections surrounded by hierarchical coronas of hubs at different ℓ levels.
for random networks25 with all nodes present (ni = 1). When λ = 1, the giant component is reduced to a tree plus one single loop (unicyclic graph), which is suddenly destroyed at the transition qc to become a tree, causing the abrupt fall of λ to zero. d, Ball(i, ℓ) of radius ℓ around node i is the set of nodes at distance ℓ from i, and ∂Ball is the set of nodes on the boundary. The shortest path from i to j is shown in red. e, Example of a weak node: a node with a small number of connections surrounded by hierarchical coronas of hubs at different ℓ levels.
Stability of the solution {νi→j = 0} requires λ(n; q) ≤ 1. The optimal influence problem for a given q (≥qc) can be rephrased as finding the optimal configuration n that minimizes the largest eigenvalue λ(n; q) (Fig. 1c). The optimal set n* of Nqc influencers is obtained when the minimum of the largest eigenvalue reaches the critical threshold:

The formal mathematical mapping of the optimal influence problem to the minimization of the largest eigenvalue of the modified non-backtracking matrix for random networks, equation (2), represents our first main result.
An example of a non-optimized solution corresponds to choosing ni at random and decoupled from the non-backtracking matrix23,27 (random percolation21, Supplementary Information section IID). In the optimized case, we seek to derandomize the selection of the set ni = 0 and optimally choose them to find the best configuration n* with the lowest qc according to equation (2). The eigenvalue λ(n) (from now on we omit q in λ(n; q) ≡ λ(n), which is always kept fixed) determines the growth rate of an arbitrary vector w0 with 2M entries after ℓ iterations of the matrix  The largest eigenvalue is then calculated by the power method:
The largest eigenvalue is then calculated by the power method:

Equation (3) is the starting point of an (infinite) perturbation series that provides the exact solution to the many-body influence problem in random networks and therefore contains all physical effects, including the collective influence. In practice, we minimize the cost energy function of influence  in equation (3) for a finite ℓ. The solution rapidly converges to the exact value as ℓ → ∞, the faster the larger the spectral gap. We find for ℓ ≥ 1, to leading order in 1/N (Supplementary Information section IIE):
in equation (3) for a finite ℓ. The solution rapidly converges to the exact value as ℓ → ∞, the faster the larger the spectral gap. We find for ℓ ≥ 1, to leading order in 1/N (Supplementary Information section IIE):

where Ball(i, ℓ) is the set of nodes inside a ball of radius ℓ (defined as the shortest path) around node i, ∂Ball(i, ℓ) is the frontier of the ball,  is the shortest path of length ℓ connecting i and j (Fig. 1d), and ki is the degree of node i.
is the shortest path of length ℓ connecting i and j (Fig. 1d), and ki is the degree of node i.
The first collective optimization in equation (4) is ℓ = 1. We find  , where Aij is the adjacency matrix (equation (39) in Supplementary Information). This term is interpreted as the energy of an antiferromagnetic Ising model with random bonds in a random external field at fixed magnetization, which is an example of a pair-wise NP-complete spin-glass whose solution is found in Supplementary Information section III with the cavity method28 (Extended Data Fig. 2).
, where Aij is the adjacency matrix (equation (39) in Supplementary Information). This term is interpreted as the energy of an antiferromagnetic Ising model with random bonds in a random external field at fixed magnetization, which is an example of a pair-wise NP-complete spin-glass whose solution is found in Supplementary Information section III with the cavity method28 (Extended Data Fig. 2).
For ℓ ≥ 2, the problem can be mapped exactly to a statistical mechanical system with many-body interactions which can be recast in terms of a diagrammatic expansion, equations (41)–(49) in Supplementary Information. For example,  leads to 4-body interactions (equation (45) in Supplementary Information), and, in general, the energy cost
leads to 4-body interactions (equation (45) in Supplementary Information), and, in general, the energy cost  contains 2ℓ-body interactions. As soon as ℓ ≥ 2, the cavity method becomes much more complicated to implement and we use another suitable method, called extremal optimization (EO)29 (Supplementary Information section IV). This method estimates the true optimal value of the threshold by finite-size scaling following extrapolation to ℓ → ∞ (Extended Data Figs 3, 4). However, EO is not scalable to find the optimal configuration in large networks. Therefore, we develop an adaptive method, which performs excellently in practice, preserves the features of EO, and is highly scalable to present-day big data.
contains 2ℓ-body interactions. As soon as ℓ ≥ 2, the cavity method becomes much more complicated to implement and we use another suitable method, called extremal optimization (EO)29 (Supplementary Information section IV). This method estimates the true optimal value of the threshold by finite-size scaling following extrapolation to ℓ → ∞ (Extended Data Figs 3, 4). However, EO is not scalable to find the optimal configuration in large networks. Therefore, we develop an adaptive method, which performs excellently in practice, preserves the features of EO, and is highly scalable to present-day big data.
The idea is to remove the nodes causing the biggest drop in the energy function, equation (4). First, we define a ball of radius ℓ around every node (Fig. 1d). Then, we consider the nodes belonging to the frontier ∂Ball(i, ℓ) and assign to node i the collective influence (CI) strength at level ℓ following equation (4):

We notice that, while equation (4) is valid only for odd radii of the ball, CIℓ(i) is defined also for even radii. This generalization is possible by considering an energy function for even radii analogous to equation (4), as explained in Supplementary Information section IIG. The case of one-body interaction with zero radius ℓ = 0 (equation (59) in Supplementary Information) leads to the high-degree (HD) ranking (equation (62) in Supplementary Information)10.
The collective influence, equation (5), is our second and most important result since it is the basis for the highly scalable and optimized CI algorithm which follows. In the beginning, all the nodes are present: ni = 1 for all i. Then, we remove node i* with highest CIℓ and set ni* = 0. The degree of each neighbour of i* is decreased by one, and the procedure is repeated to find the new top CI node to remove. The algorithm is terminated when the giant component is zero (see Supplementary Information section V for implementation, and Supplementary Information section VA for minimizing G(q) ≠ 0). By increasing the radius ℓ of the ball we obtain better and better approximations of the optimal exact solution as ℓ → ∞ (for finite networks, ℓ does not exceed the network diameter).
The collective influence CIℓ for ℓ ≥ 1 has a rich topological content, and consequently tells us more about the role played by nodes in the network than the non-interacting high-degree hub-removal strategy at ℓ = 0, CI0. The augmented information comes from the sum in the right hand side of equation (5), which is absent in the naive high-degree rank. This sum contains the contribution of the nodes living on the surface of the ball surrounding the central vertex i, each node weighted by the factor kj − 1. This means that a node placed at the centre of a corona irradiating many links—the structure hierarchically emerging at different ℓ levels as seen in Fig. 1e—can have a very large collective influence, even if it has a moderate or low degree. Such ‘weak nodes’ can outrank nodes with larger degree that occupy mediocre peripheral locations in the network. The commonly used word ‘weak’ in this context sounds particularly paradoxical. It is, indeed, usually used as a synonym for a low-degree node with an additional bridging property, which has resisted a quantitative formulation. We provide this definition through equation (5), according to which weak nodes are, de facto, quite strong. Paraphrasing Granovetter’s conundrum30, equation (5) quantifies the “strength of weak nodes”.
The CI-algorithm scales as  by removing a finite fraction of nodes at each step (Supplementary Information section VB). This high scalability allows us to find top influencers in current big-data social media and the minimal set of people to immunize in large-scale populations at the country level. The applications are investigated next.
by removing a finite fraction of nodes at each step (Supplementary Information section VB). This high scalability allows us to find top influencers in current big-data social media and the minimal set of people to immunize in large-scale populations at the country level. The applications are investigated next.
Figure 2a shows the optimal threshold qc for a random Erdös–Rényi (ER) network5 (marked by the vertical line) obtained by extrapolating the EO solution to N → ∞ and ℓ → ∞ (Supplementary Information section IV). In the same figure we compare the optimal threshold against the heuristic centrality measures: high-degree (HD)9, high-degree adaptive (HDA), PageRank (PR)7, closeness centrality (CC)6, eigenvector centrality (EC)6, and k-core12 (see Supplementary Information section I for definitions). Supplementary Information sections VI and VII show the comparison with the remaining heuristics6,11 and the Belief Propagation method of ref. 14, respectively, which have worse computational complexity (and optimality), and cannot be applied to the network sizes used here. Remarkably, at the optimal value qc predicted by our theory, the best among the heuristic methods (HDA, PR and HD) still predict a giant component ∼50–60% of the whole original network. Furthermore, the influencer threshold predicted by CI approximates very well the optimal one, and, notably, CI outperforms the other strategies. Figure 2b compares CI in scale-free (SF) networks5 against the best heuristic methods, that is, HDA and HD. In all cases, CI produces a smaller threshold and a smaller giant component (Fig. 2c).
a, G(q) in an ER network (N = 2 × 105, 〈k〉 = 3.5, error bars are s.e.m. over 20 realizations). We show the true optimal solution found with EO (‘×’ symbol), and also using CI, HDA, PR, HD, CC, EC and k-core methods. The other methods are not scalable and perform worse than HDA and are treated in Supplementary Information sections VI and VII (Extended Data Figs 8, 9). CI is close to the optimal  obtained with EO in Supplementary Information section IV. Note that EO can estimate the extrapolated optimal value of qc, but it cannot provide the optimal configuration for large systems. Inset, qc (obtained at the peak of the second-largest cluster) for the three best methods versus 〈k〉. b, G(q) for a SF network with degree exponent γ = 3, maximum degree kmax = 103, minimum degree kmin = 2 and N = 2 × 105 (error bars are s.e.m. over 20 realizations). Inset, qc versus γ. The continuous blue line is the HD analytical result computed in Supplementary Information section IIG (Extended Data Fig. 1b). c, Example of SF network with γ = 3 after the removal of 15% of nodes, using the three methods HD, HDA and CI. CI produces a much reduced giant component G (red nodes).
obtained with EO in Supplementary Information section IV. Note that EO can estimate the extrapolated optimal value of qc, but it cannot provide the optimal configuration for large systems. Inset, qc (obtained at the peak of the second-largest cluster) for the three best methods versus 〈k〉. b, G(q) for a SF network with degree exponent γ = 3, maximum degree kmax = 103, minimum degree kmin = 2 and N = 2 × 105 (error bars are s.e.m. over 20 realizations). Inset, qc versus γ. The continuous blue line is the HD analytical result computed in Supplementary Information section IIG (Extended Data Fig. 1b). c, Example of SF network with γ = 3 after the removal of 15% of nodes, using the three methods HD, HDA and CI. CI produces a much reduced giant component G (red nodes).
As an example of an information spreading network, we consider the web of Twitter users (Supplementary Information section VIII19). Figure 3a shows the giant component of Twitter when a fraction q of its influencers is removed following CI. It is surprising that a lot of Twitter users with a large number of contacts have a mild influence on the network. This is witnessed by the fact that, when CI (at ℓ = 5) predicts a zero giant component (and so it exhausts the number of optimal influencers), the scalable heuristic ranks (HD, HDA, PR and k-core) still give a substantial giant component of the order of 30–70% of the entire network. These heuristics also, inevitably, find a remarkably large number of (fake) influencers, which is at least 50% larger than that predicted by CI (Fig. 3b and Supplementary Information section VIII). One cause for the poor performance of the high-degree-based ranks is that most of the hubs are clustered, which gives a mediocre importance to their contacts. As a consequence, hubs are outranked by nodes with lower degree surrounded by coronas of hubs (shown in detail in Fig. 3c), that is, the weak nodes predicted by the theory (Fig. 1e).
a, Giant component G(q) of Twitter users19 (N = 469,013) computed using CI, HDA, PR, HD and k-core strategies (other heuristics have prohibitive running times for this system size). b, Percentage of fake influencers or false positives (PFI, equation (120) in Supplementary Information) in Twitter as a function of q, defined as the percentage of non-optimal influencers identified by the HD algorithm in comparison with CI. Below  , PFI reaches as much as ∼40%, indicating the failure of HD in optimally finding the top influencers. Indeed, to obtain G = 0, HD has to remove a much larger number of fake influencers, which at
, PFI reaches as much as ∼40%, indicating the failure of HD in optimally finding the top influencers. Indeed, to obtain G = 0, HD has to remove a much larger number of fake influencers, which at  reaches PFI ≈ 48%. c, An example of the many weak nodes found in Twitter. These crucial influencers were missed by all heuristic strategies. d, G(q) for a social network of 1.4 × 107 mobile phone users in Mexico representing an example of big data to test the scalability and performance of the algorithm in real networks. CI immunizes this social network using half a million fewer people than the best heuristic strategy (HDA), saving ∼35% of the vaccine stockpile.
reaches PFI ≈ 48%. c, An example of the many weak nodes found in Twitter. These crucial influencers were missed by all heuristic strategies. d, G(q) for a social network of 1.4 × 107 mobile phone users in Mexico representing an example of big data to test the scalability and performance of the algorithm in real networks. CI immunizes this social network using half a million fewer people than the best heuristic strategy (HDA), saving ∼35% of the vaccine stockpile.
Finally, we simulate an immunization scheme on a personal contact network built from the phone calls performed by 14 million people in Mexico (Supplementary Information section IX). Figure 3d shows that our method saves a large number of vaccines or, equivalently, finds the smallest possible set of people to quarantine; our method therefore also outranks the scalable heuristics in large real networks. Thus, while the mapping of the influencer identification problem onto optimal percolation is strictly valid for locally tree-like random networks, our results may apply also to real loopy networks, provided the density of loops is not excessively large.
Our solution to the optimal influence problem shows its importance in that it helps to unveil hitherto hidden relations between people, as witnessed by the weak-node effect. This, in turn, is the by-product of a broader notion of influence, lifted from the individual non-interacting point of view6,7,8,9,10,11,12,19,20 to the collective sphere: influence is an emergent property of collectivity, and top influencers arise from the optimization of the complex interactions they stipulate.
References
Domingos, P. & Richardson, M. Mining knowledge-sharing sites for viral marketing. In Proc. 8th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, 61–70 (ACM, 2002); http://dx.doi.org/10.1145/775047.775057
Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001)
Newman, M. E. J. Spread of epidemic disease on networks. Phys. Rev. E 66, 016128 (2002)
Kempe, D., Kleinberg, J. & Tardos, E. Maximizing the spread of influence through a social network. In Proc. 9th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, 137–143 (ACM, 2003); http://dx.doi.org/10.1145/956750.956769
Newman, M. E. J. Networks: An Introduction (Oxford Univ. Press, 2010)
Freeman, L. C. Centrality in social networks: conceptual clarification. Soc. Networks 1, 215–239 (1978)
Brin, S. & Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Networks ISDN Systems 30, 107–117 (1998)
Kleinberg, J. Authoritative sources in a hyperlinked environment. In Proc. 9th ACM-SIAM Symp. on Discrete Algorithms (1998); J. Assoc. Comput. Machinery 46, 604–632 (1999)
Albert, R., Jeong, H. & Barabási, A.-L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000)
Cohen, R., Erez, K., ben-Avraham, D. & Havlin, S. Breakdown of the Internet under intentional attack. Phys. Rev. Lett. 86, 3682–3685 (2001)
Chen, Y., Paul, G., Havlin, S., Liljeros, F. & Stanley, H. E. Finding a better immunization strategy. Phys. Rev. Lett. 101, 058701 (2008)
Kitsak, M. et al. Identification of influential spreaders in complex networks. Nature Phys. 6, 888–893 (2010)
Altarelli, F., Braunstein, A., Dall’Asta, L. & Zecchina, R. Optimizing spread dynamics on graphs by message passing. J. Stat. Mech. P09011 (2013)
Altarelli, F., Braunstein, A., Dall’Asta, L., Wakeling, J. R. & Zecchina, R. Containing epidemic outbreaks by message-passing techniques. Phys. Rev. X 4, 021024 (2014)
Hashimoto, K. Zeta functions of finite graphs and representations of p-adic groups. Adv. Stud. Pure Math. 15, 211–280 (1989)
Coja-Oghlan, A., Mossel, E. & Vilenchik, D. A spectral approach to analyzing belief propagation for 3-coloring. Combin. Probab. Comput. 18, 881–912 (2009)
Granovetter, M. Threshold models of collective behavior. Am. J. Sociol. 83, 1420–1443 (1978)
Watts, D. J. A simple model of global cascades on random networks. Proc. Natl Acad. Sci. USA 99, 5766–5771 (2002)
Pei, S., Muchnik, L., Andrade, J. S., Jr, Zheng, Z. & Makse, H. A. Searching for superspreaders of information in real-world social media. Sci. Rep. 4, 5547 (2014)
Pei, S. & Makse, H. A. Spreading dynamics in complex networks. J. Stat. Mech. P12002 (2013)
Bollobás, B. & Riordan, O. Percolation (Cambridge Univ. Press, 2006)
Bianconi, G. & Dorogovtsev, S. N. Multiple percolation transitions in a configuration model of network of networks. Phys. Rev. E 89, 062814 (2014)
Karrer, B., Newman, M. E. J. & Zdeborová, L. Percolation on sparse networks. Phys. Rev. Lett. 113, 208–702 (2014)
Angel, O., Friedman, J. & Hoory, S. The non-backtracking spectrum of the universal cover of a graph. Trans. Am. Math. Soc. 367, 4287–4318 (2015)
Krzakala, F. et al. Spectral redemption in clustering sparse networks. Proc. Natl Acad. Sci. USA 110, 20935–20940 (2013)
Newman, M. E. J. Spectral methods for community detection and graph partitioning. Phys. Rev. E 88, 042822 (2013)
Radicchi, F. Predicting percolation thresholds in networks. Phys. Rev. E 91, 010801(R) (2015)
Mézard, M. & Parisi, G. The cavity method at zero temperature. J. Stat. Phys. 111, 1–34 (2003)
Boettcher, S. & Percus, A. G. Optimization with extremal dynamics. Phys. Rev. Lett. 86, 5211–5214 (2001)
Granovetter, M. The strength of weak ties. Am. J. Sociol. 78, 1360–1380 (1973)
Acknowledgements
This work was funded by NIH-NIGMS 1R21GM107641 and NSF-PoLS PHY-1305476. Additional support was provided by Army Research Laboratory Cooperative Agreement Number W911NF-09-2-0053 (the ARL Network Science CTA). We thank L. Bo, S. Havlin and R. Mari for discussions and Grandata for providing the data on mobile phone calls.
Author information
Authors and Affiliations
Contributions
Both authors contributed equally to the work presented in this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 High-degree (HD) threshold.
a, HD influence threshold qc as a function of the degree distribution exponent γ of scale-free networks in the ensemble with kmax = mN1/(γ−1) and N → ∞. The curves refer to different values of the minimum degree m: 1 (red), 2 (blue), 3 (black). The fragility of SF networks (small qc) is notable for m = 1 (the case calculated in ref. 10). In this case (m = 1), the network contains many leaves, and reduces to a star at γ = 2, which is trivially destroyed by removing the only single hub, explaining the general fragility in this case. Furthermore, in this same case, the network becomes a collection of dimers with k = 1 when γ → ∞, which is still trivially fragile. This also explains why qc → 0 for γ ≥ 4. Therefore, the fragility in the case m = 1 has its roots in these two limiting trivial cases. Removing the leaves (m = 2) results in a 2-core, which is already more robust. For the 3-core m = 3, qc ≈ 0.4–0.5 provides a quite robust network, and has the expected asymptotic limit to a non-zero qc of a random regular graph with k = 3 as γ → ∞, qc → (k − 2)/(k − 1) = 0.5. Thus, SF networks become robust in these more realistic cases, and the search for other attack strategies becomes even more important. b, HD influence threshold qc as a function of the degree distribution exponent of scale-free networks with minimum degree m = 2 in the ensemble where kmax is fixed and does not scale with N. The curves refer to different values of the cut-off kmax: 102 (red), 103 (green), 105 (blue), 108 (magenta), and kmax = ∞ (black), and show that for a typical kmax degree of 103, for instance in social networks, the network is fairly robust with qc ≈ 0.2 for all γ. The curve with m = 2 and kmax = 103 is replotted in the inset of Fig. 2b.
Extended Data Figure 2 Replica Symmetry (RS) estimation of the maximum eigenvalue.
Main panel, the eigenvalue  , equation (92) in Supplementary Information for the two-body interaction ℓ = 1, obtained by minimizing the energy function
, equation (92) in Supplementary Information for the two-body interaction ℓ = 1, obtained by minimizing the energy function  with the RS cavity method. The curve was computed on an ER graph of N = 10,000 nodes and average degree 〈k〉 = 3.5 and then averaged over 40 realizations of the network (error bars are s.e.m.). Inset, comparison between the RS cavity method and EO (extremal optimization) for an ER graph of 〈k〉 = 3.5 and N = 128. The curves are averaged over 200 realizations (error bars are s.e.m.).
with the RS cavity method. The curve was computed on an ER graph of N = 10,000 nodes and average degree 〈k〉 = 3.5 and then averaged over 40 realizations of the network (error bars are s.e.m.). Inset, comparison between the RS cavity method and EO (extremal optimization) for an ER graph of 〈k〉 = 3.5 and N = 128. The curves are averaged over 200 realizations (error bars are s.e.m.).
Extended Data Figure 3 EO estimation of the maximum eigenvalue.
Eigenvalue λ(q) obtained by minimizing the energy function  (n) with τEO (τ-extremal optimization), plotted as a function of the fraction of removed nodes q. The panels are for different orders of the interactions. The curves in each panel refer to different sizes of ER networks with average connectivity 〈k〉 = 3.5. Each curve is an average over 200 instances (error bars are s.e.m.). The value qc where λ(qc) = 1 is the threshold for a particular N and many-body interaction.
(n) with τEO (τ-extremal optimization), plotted as a function of the fraction of removed nodes q. The panels are for different orders of the interactions. The curves in each panel refer to different sizes of ER networks with average connectivity 〈k〉 = 3.5. Each curve is an average over 200 instances (error bars are s.e.m.). The value qc where λ(qc) = 1 is the threshold for a particular N and many-body interaction.
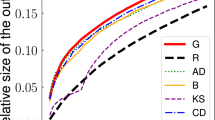
Extended Data Figure 4 Estimation of optimal threshold  with EO.
with EO.
a, Critical threshold qc as a function of the system size N, obtained with EO from Extended Data Fig. 3, of ER networks with 〈k〉 = 3.5 and varying size. The curves refer to different orders of the many-body interactions. The data show a linear behaviour as a function of N−2/3, typical of spin glasses, for each many-body interaction ρ. The extrapolated value  is obtained at the y intercept. b, Thermodynamic critical threshold
is obtained at the y intercept. b, Thermodynamic critical threshold  as a function of the order of the interactions ρ from a. The data scale linearly with 1/ρ. From the y intercept of the linear fit we obtain the thermodynamic limit of the infinite-body optimal value
as a function of the order of the interactions ρ from a. The data scale linearly with 1/ρ. From the y intercept of the linear fit we obtain the thermodynamic limit of the infinite-body optimal value  .
.
Extended Data Figure 5 Comparison of the CI algorithm for different radii ℓ of the Ball(ℓ).
We use ℓ = 1, 2, 3, 4, 5, on a ER graph with average degree 〈k〉 = 3.5 and N = 105 (the average is taken over 20 realizations of the network, error bars are s.e.m.). For ℓ = 3 the performance is already practically indistinguishable from ℓ = 4, 5. The stability analysis we developed to minimize qc is strictly valid only when G = 0, since the largest eigenvalue of the modified NB matrix controls the stability of the solution G = 0, and not the stability of the solution G > 0. In the region where G > 0 we use a simple and fast procedure to minimize G explained in Supplementary Information section VA. This explains why there is a small dependence on having a slightly larger G for larger ℓ, when G > 0 in the region q ≈ 0.15.
Extended Data Figure 6 Illustration of the algorithm used to minimize G(q) for q < qc.
Starting from the completely fragmented network at q = qc, the Nqc influencers are reinserted with their original degree and connected to their original neighbours with the following criterion: each node is assigned and index c(i) given by the number of clusters it would join if it were reinserted in the network. For example, the red node has c(red) = 2, while the blue one has c(blue) = 3. The node with the smallest c(i) is reinserted in the network: in this case the red node. Then the c(i)s are recalculated and the new node with the smallest c(i) is found and reinserted. These steps are repeated until all the removed nodes are reinserted in the network.
Extended Data Figure 7 Test of the decimation fraction.
Giant component G as a function of the fraction of removed nodes q using CI, for an ER network of N = 105 nodes and average degree 〈k〉 = 3.5. The profiles of the curves are drawn for different percentages of nodes fixed at each step of the decimation algorithm.
Extended Data Figure 8 Comparison of the performance of CI, BC and EGP in destroying G.
We also include HD, HDA, EC, CC, k-core and PR. We use a scale-free (SF) network with degree exponent γ = 2.5, average degree 〈k〉 = 4.68, and N = 104. We use the same parameters as in ref. 11.
Extended Data Figure 9 Comparison with BP for a network immunization.
a, Fraction of infected nodes f as a function of the fraction of immunized nodes q in the susceptible-infected-removed (SIR) model from the BP solution. We use an ER random graph of N = 200 nodes and average degree 〈k〉 = 3.5. The fraction of initially infected nodes is p = 0.1 and the inverse temperature β = 3.0. The profiles are drawn for different values of the transmission probability w: 0.4 (red curve), 0.5 (green), 0.6 (blue), 0.7 (magenta). Also shown are the results of the fixed density BP algorithm (open circles). b, Chemical potential μ as a function of the immunized nodes q from BP. We use an ER random graph of N = 200 nodes and average degree 〈k〉 = 3.5. The fraction of the initially infected nodes is p = 0.1 and the inverse temperature β = 3.0. The profiles are drawn for different values of the transmission probability w: 0.4 (red curve), 0.5 (green), 0.6 (blue), 0.7 (magenta). Also shown are the results of the fixed density BP algorithm (open circles) for the region where the chemical potential is non-convex. c, Comparison between the giant components obtained with CI, HDA, HD and BP. We use an ER network of N = 103 and 〈k〉 = 3.5. We also show the solution of CI from Fig. 2a for N = 105. We find in order of performance: CI, HDA, BP and HD. (The average is taken over 20 realizations of the network, error bars are s.e.m.) d, Comparison between the giant components obtained with CI, HDA, HD and BPD. We use a SF network with degree exponent γ = 3.0, minimum degree kmin = 2, and N = 104 nodes.
Extended Data Figure 10 Fraction of infected nodes f(q) as a function of the fraction of immunized nodes q in SIR from BP.
We use the following parameters: initial fraction of infected people p = 0.1, and transmission probability w = 0.5. We use an ER network of N = 103 nodes and 〈k〉 = 3.5. We compare CI, HDA and BP. All strategies give similar performance, owing to the large value of the initial infection p, which washes out the optimization performed by any sensible strategy, in agreement with the results shown in figure 12a of ref. 14.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data and Supplementary References. (PDF 1656 kb)
Rights and permissions
About this article
Cite this article
Morone, F., Makse, H. Influence maximization in complex networks through optimal percolation. Nature 524, 65–68 (2015). https://doi.org/10.1038/nature14604
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature14604
This article is cited by
-
Protein–protein interaction network-based integration of GWAS and functional data for blood pressure regulation analysis
Human Genomics (2024)
-
Robustness and resilience of complex networks
Nature Reviews Physics (2024)
-
Identifying key players in complex networks via network entanglement
Communications Physics (2024)
-
DomiRank Centrality reveals structural fragility of complex networks via node dominance
Nature Communications (2024)
-
An insight into topological, machine and Deep Learning-based approaches for influential node identification in social media networks: a systematic review
Multimedia Systems (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.






 with EO.
with EO.