Abstract
The concepts and ideas of coherent, nonlinear and quantum optics have been extended to photon energies in the range of 10–100 kiloelectronvolts, corresponding to soft γ-ray radiation (the term used when the radiation is produced in nuclear transitions) or, equivalently, hard X-ray radiation (the term used when the radiation is produced by electron motion). The recent experimental achievements in this energy range include the demonstration of parametric down-conversion in the Langevin regime1, electromagnetically induced transparency in a cavity2, the collective Lamb shift3, vacuum-assisted generation of atomic coherences4 and single-photon revival in nuclear absorbing multilayer structures5. Also, realization of single-photon coherent storage6 and stimulated Raman adiabatic passage7 were recently proposed in this regime. More related work is discussed in a recent review8. However, the number of tools for the coherent manipulation of interactions between γ-ray photons and nuclear ensembles remains limited. Here we suggest and implement an efficient method to control the waveforms of γ-ray photons coherently. In particular, we demonstrate the conversion of individual recoilless γ-ray photons into a coherent, ultrashort pulse train and into a double pulse. Our method is based on the resonant interaction of γ-ray photons with an ensemble of nuclei with a resonant transition frequency that is periodically modulated in time. The frequency modulation, which is achieved by a uniform vibration of the resonant absorber, owing to the Doppler effect, renders resonant absorption and dispersion both time dependent, allowing us to shape the waveforms of the incident γ-ray photons. We expect that this technique will lead to advances in the emerging fields of coherent and quantum γ-ray photon optics, providing a basis for the realization of γ-ray-photon/nuclear-ensemble interfaces and quantum interference effects at nuclear γ-ray transitions.
Similar content being viewed by others
Main
Quantum optics deals with the interaction of photons with the quantum transitions of matter, providing the basis for the new, fast-growing fields of quantum cryptography, quantum communication and quantum information (see, for example, ref. 9 and references therein). So far, experiments in these fields have been implemented with either microwave or optical photons interacting with atomic transitions, and typically require cryogenic temperatures.
The γ-ray photons (for which we use the shorthand ‘γ-photons’) in the 10–100-keV energy range have important potential advantages over the microwave and optical photons for applications in quantum cryptography, communication and information, for a number of reasons. First, with such photons there is nearly 100% detector efficiency and low noise (almost no false detections). Second, there is extremely high (potentially sub-ångström and, at the moment, nanometre10) spatial resolution. This removes what is now a fundamental limitation on the creation of nanoscale photonic circuits set by the diffraction limit, which is ∼1 µm for optical photons. Third, they have a high penetration depth in many materials that are opaque to optical photons. Fourth, with such photons the capacity of information channels is potentially much higher.
Nuclear transitions in solids in this energy range have a number of advantages compared with electronic optical transitions. They may present perfect two-level systems with very narrow linewidths (for example 1.1 MHz for the 14.4-keV transition in 57Fe) owing to the Mössbauer effect (even at room temperature) and deep shielding from the environment. The quality factor for the 14.4-keV transition is Q = 3 × 1012, as per definition: Q is the ratio of resonance energy to bandwidth. Coherent multiple scattering of a γ-photon in an optically thick, resonant absorber enables potential applications for single γ-photon/nuclear-ensemble interfaces owing to the collective enhancement of the photon–nucleus interaction. We note that in the optical range such single-photon/atomic-ensemble interfaces have been developed recently as a powerful alternative to cavity-enhanced single-photon/single-atom interfaces11. Moreover, natural sources of single γ-photons exist in the form of low-activity radioactive sources, for which discrete emissions well separated in time (compared with the natural lifetime of the level) ensure the single-photon nature of the radiation. Also, the cascade scheme of the decay, characteristic of some radioactive Mössbauer sources (for example 57Co; Fig. 1a), ensures heralding of the emission of the second γ-photon by detection of the first γ-photon in the cascade, which ‘starts the clock’ for measuring the waveform of the second photon12.
a, The 57Co nuclide in the state |d〉 decays with half-life of T1/2 = 272 d, producing an 57Fe nucleus in the state |c〉, which decays with a lifetime of Tc = 12 ns to the state |b〉, emitting a 122-keV γ-photon. The state |b〉 decays with lifetime of Tr = 141 ns to the ground state, |a〉, emitting a 14.4-keV photon. b, The 14.4-keV transition between the ground state, |1〉, and the first excited state, |2〉, of the absorbing 57Fe nucleus with the linewidth 1.13 MHz.
The methods for coherently controlling temporal waveforms of single photons (well developed in optics owing to the use of high-finesse cavities and bright, coherent sources of radiation) are limited in γ-optics, although the emerging state-of-the-art facilities, such as self-seeded hard X-ray free-electron lasers13 and nearly 100% reflecting mirrors14, will provide an impetus for the development of such techniques.
We propose an efficient method to shape γ-photons in an optically thick, uniformly vibrating, resonant, recoilless absorber, and perform a proof-of-principle experiment with a 57Co source of single γ-photons and a 57Fe absorber (Fig. 1).
The basic idea is that the vibration of an absorber leads to periodic modulation of the resonant  nuclear transition frequency (Fig. 1b) with respect to the frequency of the incident photons owing to the Doppler effect. As a result, the quasi-monochromatic incident radiation is transformed during its propagation into a spectral comb at the point where it exits the absorber. The relative amplitudes and phases of the produced spectral components are defined by the vibration amplitude and frequency, the detuning of the central frequency of the source from the resonant frequency of the absorber, the source and absorber linewidths, and the absorber optical depth. By changing these parameters, we can adjust the amplitudes and phases of the output spectral components and produce waveforms different from the incident γ-photons. In particular, the creation of a constant phase difference between equidistant neighbouring spectral components of comparable amplitude would result in a sequence of pronounced, bandwidth-limited pulses.
nuclear transition frequency (Fig. 1b) with respect to the frequency of the incident photons owing to the Doppler effect. As a result, the quasi-monochromatic incident radiation is transformed during its propagation into a spectral comb at the point where it exits the absorber. The relative amplitudes and phases of the produced spectral components are defined by the vibration amplitude and frequency, the detuning of the central frequency of the source from the resonant frequency of the absorber, the source and absorber linewidths, and the absorber optical depth. By changing these parameters, we can adjust the amplitudes and phases of the output spectral components and produce waveforms different from the incident γ-photons. In particular, the creation of a constant phase difference between equidistant neighbouring spectral components of comparable amplitude would result in a sequence of pronounced, bandwidth-limited pulses.
The discussed method to produce ultrashort γ-ray pulses essentially constitutes a γ-ray implementation of a general approach based on the ultrafast variation of the parameters of a resonant quantum transition (see ref. 15 and references therein). Whereas in the case of atomic transitions the modulation of the transition frequency was produced by the quasi-static Stark effect in a strong laser field, in the case of nuclear transitions it is due to the Doppler effect. This resonant parametric technique, unlike the traditional techniques of nonlinear optics, does not require a high intensity of incoming radiation and, hence, can be implemented even in the single-photon regime.
The frequency modulation of recoilless emission by mechanical vibration has been intensively studied since the late 1970s in applications to spectroscopic measurements and the calibration of mechanical displacements (see refs 16, 17 and references therein). Recently, there was a suggestion to produce ultrashort γ-pulses using a vibrating source, emitting frequency-modulated radiation, with a far-off-resonance absorber compensating the phase mismatch of the incident γ-radiation spectral components18. Although sound in principle, that proposal is difficult to implement experimentally, because weak non-resonant interaction requires an absorber so thick that off-resonance losses are undesirably large. Use of a resonant absorber resolves that problem. Also, in practice it is easier to realize uniform oscillations of a thin, resonant absorber than of a radiative source.
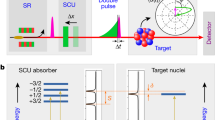
The scheme of our experimental set-up is given in Fig. 2. Observation of a single-photon waveform, shaped by the vibrating, resonant absorber, is based on the time-delayed coincidence counts of the sequentially emitted 122-keV and 14.4-keV γ-photons (Fig. 1a). Registering a 122-keV photon defines the initial moment, t0, of the formation of the 14.4-keV state and the beginning of photon emission (equation (2); all numbered equations are in Methods). We measure the delay, τ = t − t0, in the detection of the 14.4-keV photon at the exit of the absorber with a 5-ns bin width, repeating this procedure many times. As a result, we obtain the coincidence count rate, as a function of delay, N(τ), corresponding to the single-photon waveform  (refs 5, 12, 16–21). These experiments are essentially inspired by the recent demonstration of a new technique for optical single-photon shaping22.
(refs 5, 12, 16–21). These experiments are essentially inspired by the recent demonstration of a new technique for optical single-photon shaping22.
The emitter (E) is a radioactive 57Co:Rh foil. It can be moved by the Mössbauer transducer with tunable constant velocity, Vem, relative to the absorber (A), which is 25-μm-thick stainless-steel foil with a natural abundance (∼2%) of 57Fe (optical depth, TM = 5.18). It is glued on the polyvinylidene fluoride piezo-transducer that transforms the sinusoidal signal from the radio-frequency generator (G) into the uniform vibration (R, vibration amplitude). The time-to-amplitude converter (TAC), operating in the coincidence mode, receives the ‘start’ pulse, produced by detector D1 on registration of a 122-keV photon, and the ‘stop’ pulse, produced by detector D2 on registration of a 14.4-keV photon transmitted by the vibrating absorber. The delay, τ, between the stop and start pulses is measured by the pulse-height analyser (PHA). At times  , matching the chosen vibration phase,
, matching the chosen vibration phase,  , the generator also produces ‘gate-in’ signals, allowing TAC and PHA to measure the τ provided that the 122-keV photon is received only within the short interval between
, the generator also produces ‘gate-in’ signals, allowing TAC and PHA to measure the τ provided that the 122-keV photon is received only within the short interval between  and
and  .
.
Transmission through the absorber vibrating with frequency Ω results in the reshaping of the exponential waveform of the incident photon. The output shape depends on the vibration phase,  , at time t0, but because emission of 122-keV photon is a stochastic process,
, at time t0, but because emission of 122-keV photon is a stochastic process,  is random. To reveal the coherent effect of the absorber vibration on the 14.4-keV-photon waveform, we collect only the coincidence counts of 122-keV photons and those 14.4-keV photons whose 122-keV photons were detected within short intervals,
is random. To reveal the coherent effect of the absorber vibration on the 14.4-keV-photon waveform, we collect only the coincidence counts of 122-keV photons and those 14.4-keV photons whose 122-keV photons were detected within short intervals,  , around the times
, around the times  , where n = 0, 1, 2, … (Fig. 2), corresponding to the same vibration phase,
, where n = 0, 1, 2, … (Fig. 2), corresponding to the same vibration phase,  .
.
This technique allowed us to demonstrate the temporal compression of an individual γ-photon into a decaying train of ultrashort pulses that were an order of magnitude shorter than the decay time of the excited nuclear state (Fig. 3b). In the following, we show experimental results that were obtained under conditions leading to pulses with maximum peak height for the given absorber thickness.
a, Spectrum of the incident 14.4-keV-photon waveform in the reference frame of the vibrating absorber and in the laboratory reference frame (inset), calculated according to equation (5) (blue solid and red dashed lines are spectral amplitudes and phases, respectively). Central phases of the lower-frequency, principle-frequency and upper-frequency components are labelled by triangles, circle and squares, respectively. The vibration frequency, phase and amplitude (modulation index) are respectively Ω/2π = 10.2 MHz,  and R = 0.25 Å (p = 1.8). a.u., arbitrary units. b, The normalized coincidence count rate of 14.4-keV photons, N(τ)/N(0), passed through the vibrating absorber (γ-photon waveform). The ‘−1’ sideband is tuned to the absorber spectral line by moving the emitter towards the absorber with velocity Vem = 0.88 mm s−1. The experimental data are blue dots, the background is subtracted and the error bars are estimated from photon counting statistics as
and R = 0.25 Å (p = 1.8). a.u., arbitrary units. b, The normalized coincidence count rate of 14.4-keV photons, N(τ)/N(0), passed through the vibrating absorber (γ-photon waveform). The ‘−1’ sideband is tuned to the absorber spectral line by moving the emitter towards the absorber with velocity Vem = 0.88 mm s−1. The experimental data are blue dots, the background is subtracted and the error bars are estimated from photon counting statistics as  . Red solid and dashed curves are plotted according to equation (11) and equation (3), respectively. Upper inset, sinusoidal vibration of the absorber and the acquisition interval, Ωdt = π/2, limited by the equipment used. Lower inset, the single-photon waveform in the case where the ‘+1’ sideband is tuned to the absorber resonance. c, The 14.4-keV-photon waveform in the case where Ω/2π = 2.6 MHz,
. Red solid and dashed curves are plotted according to equation (11) and equation (3), respectively. Upper inset, sinusoidal vibration of the absorber and the acquisition interval, Ωdt = π/2, limited by the equipment used. Lower inset, the single-photon waveform in the case where the ‘+1’ sideband is tuned to the absorber resonance. c, The 14.4-keV-photon waveform in the case where Ω/2π = 2.6 MHz,  , R = 0.9 Å (p = 6.58), the emitter is moved towards the absorber with velocity Vem = 1.13 mm s−1 (tuning the ‘−5’ sideband to the absorber resonance), and the acquisition interval is π/8 (upper inset). Lower inset, the 14.4-keV-photon waveform under the same conditions, except that Vem = −1.13 mm s−1 (tuning the ‘+5’ sideband to the absorber resonance).
, R = 0.9 Å (p = 6.58), the emitter is moved towards the absorber with velocity Vem = 1.13 mm s−1 (tuning the ‘−5’ sideband to the absorber resonance), and the acquisition interval is π/8 (upper inset). Lower inset, the 14.4-keV-photon waveform under the same conditions, except that Vem = −1.13 mm s−1 (tuning the ‘+5’ sideband to the absorber resonance).
The physical origin of the waveform transformation is revealed by spectral analysis. The spectrum (Fig. 3a, inset) of the quasi-monochromatic incoming photon (Fig. 3b, red dashed curve) in the laboratory reference frame is ‘seen’ by the vibrating nuclei of the absorber as a comb of equidistant spectral components separated by the vibration frequency, Ω (Fig. 3a and equations (4) and (5)). Under the chosen modulation index, p = 1.8 (see Methods), there are seven major spectral components. It can be seen that the upper-frequency sidebands are phase-matched with a phase difference of π between each neighbouring pair (brown squares), whereas three lower-frequency sidebands are phase matched with a phase difference of 0 (green triangles). Taking into account the equivalence of 2πn-shifted phases of the ‘−2’ and ‘+2’ sidebands (Fig. 3a), we can match five major spectral components, eliminating either the ‘−1’ or the ‘+1’ sideband by tuning it to the absorber resonance (by properly choosing the constant velocity of the source with respect to the absorber). This leads to the waveforms shown by the red line in Fig. 3b (elimination of ‘−1’) and blue line in the inset of Fig. 3b (elimination of ‘+1’). In terms of the shift of the produced pulse train relative to the front edge of the photon, these waveforms differ from each other by half the vibration cycle, π/Ω. Owing to constructive interference of the generated sidebands, the peak values of the count rate rise above the exponential waveform of the incident photon. Even higher peak heights will be achieved if, instead of suppression of the phase-mismatched sideband through resonant absorption, its phase is shifted by π through resonant dispersion. Such a phase shift requires detuning from the exact resonance and a several-fold greater resonant optical depth; without strong off-resonance photoelectric absorption, it can be realized in a stainless-steel film highly enriched with 57Fe.
We also demonstrate the possibility of a single photon splitting into two pulses (Fig. 3c), for the first time realizing a time-bin qubit in the γ-ray frequency range23. The time interval between the pulses and the ratio of their amplitudes can be controlled by the vibration phase (Methods).
A direct count rate of the whole flow of the 14.4-keV photons versus time starting from  (without binding to the 122-keV photons) corresponds to averaging the 14.4-keV-photon count rate, N(t − t0), over the time t0 (equation (12)). In this case, the random flow of γ-photons transforms into a train of nanosecond pulses (Fig. 4). The pulse repetition period is equal to 2π/Ω, and the pulse duration is defined by the inverse of the product of the number of phase-matched components (proportional to the modulation index) and the modulation frequency. An increase in the vibration frequency at a fixed vibration amplitude results in a proportional shortening of both the pulse duration and the repetition period, owing to an increase in the separation between the sidebands (compare Fig. 4a with Fig. 4b and Fig. 4c with Fig. 4d). An increase in the vibration amplitude at a fixed vibration frequency results in a pulse shortening without change in the repetition period, owing to an increase in the number of sidebands (compare Fig. 4a with Fig. 4c and Fig. 4b with Fig. 4d). However, the short, intense pulses are accompanied by the additional weak pulses appearing as a result of the phase-mismatched components.
(without binding to the 122-keV photons) corresponds to averaging the 14.4-keV-photon count rate, N(t − t0), over the time t0 (equation (12)). In this case, the random flow of γ-photons transforms into a train of nanosecond pulses (Fig. 4). The pulse repetition period is equal to 2π/Ω, and the pulse duration is defined by the inverse of the product of the number of phase-matched components (proportional to the modulation index) and the modulation frequency. An increase in the vibration frequency at a fixed vibration amplitude results in a proportional shortening of both the pulse duration and the repetition period, owing to an increase in the separation between the sidebands (compare Fig. 4a with Fig. 4b and Fig. 4c with Fig. 4d). An increase in the vibration amplitude at a fixed vibration frequency results in a pulse shortening without change in the repetition period, owing to an increase in the number of sidebands (compare Fig. 4a with Fig. 4c and Fig. 4b with Fig. 4d). However, the short, intense pulses are accompanied by the additional weak pulses appearing as a result of the phase-mismatched components.
Count rate of the 14.4-keV photons versus time in the case where detector D1 is removed and the ‘gate-in’ signal, matched with the zero phase of vibration, triggers TAC and PHA to measure time elapsed until detector D2 produces a ‘stop’ signal on registration of 14.4-keV photon. Repeating this procedure many times results in a count rate of the 14.4-keV photons versus time corresponding to the intensity of 14.4-keV radiation. The constant velocity, Vem, of the emitter towards the absorber tunes the ‘−1’ sideband to the absorber resonance (Fig. 3a). a, Ω/2π = 5.16 MHz, Vem = 0.44 mm s−1, R = 0.25 Å, (p = 1.8); b, Ω/2π = 10.2 MHz, Vem = 0.87 mm s−1, R = 0.25 Å (p = 1.8); c, Ω/2π = 5.16 MHz, Vem = 0.44 mm s−1, R = 0.27 Å (p = 2); d, Ω/2π = 10.2 MHz, Vem = 0.87 mm s−1, R = 0.27 Å (p = 2). The experimental data are blue dots and the error bars are estimated from photon counting statistics as above. The red solid line is plotted according to equations (13) and (14).
The maximum potentially available vibration frequency is 1 GHz with rather small modulation index, p < 2. A much higher modulation index (p > 10) may be achieved with moderate modulation frequencies (10–100 MHz), but in this case additional care should be taken in phase-matching the produced sidebands (using, for example, a chain of properly tuned resonantly absorbing foils or external phase synchronization by the diffraction gratings). Thus, the shortest pulses, which potentially could be produced by that technique, are limited to 100 ps (unless other methods providing higher modulation frequency and higher modulation index of the nuclear transition are used).
The described set-up is at present the only known tabletop source of ultrashort γ-ray pulses. The parameters of the pulses, including the shape and number of pulses, the repetition rate (potentially variable in the megahertz–gigahertz range) and the duration (potentially 100 ns–100 ps), can be widely controlled. This allows for a variety of time-resolved experiments (including dynamic X-ray diffraction) directly in local labs, although such a tabletop set-up cannot compete, in terms of pulse duration and photon flux, with modern synchrotrons24. However, it has two unique features leading to applications that are unavailable with other existing sources of ultrashort X-ray pulses.
First, the produced pulses have exclusive spectral–temporal properties. At the moment, they are the only nearly transform-limited ultrashort pulses that can be produced in this frequency range. They can be used to generate frequency combs with a fixed frequency interval and phase-matched spectral components, providing a unique combination of wide spectral coverage and narrow spectral width for each component. Such pulses are promising for the realization of frequency comb spectroscopy (broadband, high-spectral-resolution spectroscopy) of nuclei in solids in the 10–100-keV energy range as well as time-resolved Mössbauer spectroscopy. They can also be used for efficient preparation of a coherent superposition of nuclear states, and for realization of quantum interference effects such as modulation-induced transparency25 and electromagnetically induced transparency26,27. The last effect has numerous applications in the optical frequency range, such as the implementation of resonantly enhanced nonlinearities (including single-photon nonlinearities), slow and stored light, lasing without inversion, and so on (see ref. 28 and references therein). Similar applications may be anticipated in the γ-ray range.
Second, at the moment our tabletop set-up is the only source of single-photon, ultrashort pulses with efficiently controllable waveforms. The splitting of the single photon into two pulses constitutes the first realization of a time-bin qubit in this range of frequencies. The production of single-photon, ultrashort-pulse trains with pulse duration much shorter than the natural lifetime of the emitting nuclear level and with controllable waveforms provides a unique opportunity for the realization of quantum memories29,30 and other nuclear-ensemble/γ-photon interfaces, opening the way to applications in quantum communication and information.
Methods Summary
The transformation of a recoilless, spontaneously emitted γ-photon on its propagation through a uniformly vibrating, resonant Mössbauer absorber is described semiclassically by numerically and analytically solving the Maxwell–Bloch equations with a harmonically modulated nuclear transition frequency in the rotating-wave and linear approximations. Modification of the shape of the γ-photon at the exit of the absorber is studied as a function of the parameters of the system, such as the frequency and amplitude of modulation, the detuning of the central frequency of the source from the resonance frequency of the absorber, and the vibration phase at the time of the γ-photon arriving at the absorber entrance.
We numerically plot waveforms for different parameter values to demonstrate how to produce a variety of waveforms from a single γ-photon (including a decaying train of ultrashort pulses, a double pulse and a single triangular pulse). The regime of formation of a train of γ-ray pulses with pulse-to-pulse coherence and a duration an order of magnitude less than the natural relaxation time of the resonant nuclear transition is described analytically within a simplified model.
Online Methods
The transformation of a recoilless γ-photon in a uniformly (piston-like) vibrating Mössbauer absorber can be considered as follows. The resonant absorber vibrates along the direction of propagation of the photon with amplitude R and frequency Ω/2π (Fig. 2). The vibration set-up was designed to provide uniform vibration of the absorber as a solid body. In particular, a small absorber thickness, L  2πVs/Ω, where Vs is the speed of sound in the absorber, ensures that the internal vibrational modes have frequencies far beyond Ω and are not excited by the absorber vibration. Correspondingly, the coordinate z′ in the reference frame of the vibrating absorber is related to the coordinate z in the laboratory reference frame by the relation
2πVs/Ω, where Vs is the speed of sound in the absorber, ensures that the internal vibrational modes have frequencies far beyond Ω and are not excited by the absorber vibration. Correspondingly, the coordinate z′ in the reference frame of the vibrating absorber is related to the coordinate z in the laboratory reference frame by the relation

The electric field of an individual 14.4-keV γ-photon emitted by the radioactive source, Er(z, t), in the laboratory reference frame is represented by a classical quasi-monochromatic wave3,4,8,17,19

where θ(x) is the Heaviside step function, τ = t − t0 is the time passed from detection of the preceding 122-keV photon at the moment t0 (Fig. 1a), Γr = 1/Tr (Γr/2π is the linewidth of the source and Tr is the natural lifetime of the state |b〉), ωr/2π is the carrier frequency of the emitted photon, c is the speed of light in vacuum and φ0 is the random phase. The propagation distance of the photon from the emitter both to the absorber and to the detector satisfies the condition Δz  cδτ, where δτ is the measurement error. Therefore, the count rate of the emitted photons in front of the absorber, calculated from equation (2), has the form (red dashed lines in Fig. 3b, c):
cδτ, where δτ is the measurement error. Therefore, the count rate of the emitted photons in front of the absorber, calculated from equation (2), has the form (red dashed lines in Fig. 3b, c):

In the reference frame co-moving with the absorber, the electric field in equation (2) takes the form

where  = Ωt0, Jn(p) is the Bessel function of the first kind of order n (n is the integer number), p = 2πR/λ is the modulation index and λ = 2πc/ωr is the photon wavelength. Equation (4) results from substitution of equation (1) into equation (2) in the nonrelativistic approximation, assuming that Γr
= Ωt0, Jn(p) is the Bessel function of the first kind of order n (n is the integer number), p = 2πR/λ is the modulation index and λ = 2πc/ωr is the photon wavelength. Equation (4) results from substitution of equation (1) into equation (2) in the nonrelativistic approximation, assuming that Γr  ωr and taking into account
ωr and taking into account  as well as
as well as  . Thus, the incident electric field ‘seen’ by the vibrating nuclei is frequency modulated and corresponds to a superposition of exponentially decaying spectral components with the carrier frequencies ωr ± nΩ. The amplitudes and phases of the sidebands are determined by the modulation index, p, through the magnitudes and signs of Bessel functions of corresponding orders, Jn(p). Thus, ‘±n’ sidebands, located symmetrically with respect to the carrier frequency, ωr, have the same amplitudes, and their phases differ by nπ.
. Thus, the incident electric field ‘seen’ by the vibrating nuclei is frequency modulated and corresponds to a superposition of exponentially decaying spectral components with the carrier frequencies ωr ± nΩ. The amplitudes and phases of the sidebands are determined by the modulation index, p, through the magnitudes and signs of Bessel functions of corresponding orders, Jn(p). Thus, ‘±n’ sidebands, located symmetrically with respect to the carrier frequency, ωr, have the same amplitudes, and their phases differ by nπ.
The Fourier transform,  , of the field of the incident γ-photon (equation (4)) in the case of a short, as compared with the photon length, propagation distance, Δz′
, of the field of the incident γ-photon (equation (4)) in the case of a short, as compared with the photon length, propagation distance, Δz′  cTr, yields a representation in the form of the spectral comb
cTr, yields a representation in the form of the spectral comb

For p = 1.8, which maximizes  , this structure is shown in Fig. 3a, where the blue line represents the squared spectral amplitudes and the red line represents the spectral phases, respectively. With an increase in modulation index, a larger number of sidebands is produced.
, this structure is shown in Fig. 3a, where the blue line represents the squared spectral amplitudes and the red line represents the spectral phases, respectively. With an increase in modulation index, a larger number of sidebands is produced.
Evolution of the electric field of the photon, E(z′, τ), during its propagation through the absorber ( ), is described by the wave equation
), is described by the wave equation

where  ,
,  is the background dielectric permittivity of the absorber, δe takes into account the non-resonant losses due primarily to the photoelectric absorption, and P is the resonant nuclear polarization, related to the coherence, ρ21, of the resonant nuclear transition
is the background dielectric permittivity of the absorber, δe takes into account the non-resonant losses due primarily to the photoelectric absorption, and P is the resonant nuclear polarization, related to the coherence, ρ21, of the resonant nuclear transition

via the probability of recoilless absorption, fa, the concentration of the resonant nuclei, N, and the dipole moment, d12, of the resonant transition  (Fig. 1b). Because the photons are depolarized and the dipole moments are randomly oriented, we can neglect the vector character of E, P and d12. The density matrix equation for the coherence of the resonant absorber transition has the form
(Fig. 1b). Because the photons are depolarized and the dipole moments are randomly oriented, we can neglect the vector character of E, P and d12. The density matrix equation for the coherence of the resonant absorber transition has the form

where ωa/2π is the frequency of the resonant transition, γa/2π is the half-linewidth of its spectral line and  is the population difference between the energy levels |1〉 and |2〉.
is the population difference between the energy levels |1〉 and |2〉.
We seek a solution of equations (6)–(8) in the form  , where F stands for E or P. In the rotating-wave approximation (|ω – ωa|
, where F stands for E or P. In the rotating-wave approximation (|ω – ωa| |ω + ωa|), from equations (7) and (8) we find that
|ω + ωa|), from equations (7) and (8) we find that

Fourier transforming equation (6), implementing the slowly-varying-envelope approximation ( ,
,  ) and using equation (9) results in the following equation for the field:
) and using equation (9) results in the following equation for the field:

where  is the Mössbauer optical thickness. The solution of equation (10), satisfying the input boundary condition
is the Mössbauer optical thickness. The solution of equation (10), satisfying the input boundary condition  (equation (5)), has the form of a spectral comb:
(equation (5)), has the form of a spectral comb:

This gives us the time dependence of the output field emerging from the absorber both in the vibrating reference frame,  , and in the laboratory frame of reference,
, and in the laboratory frame of reference,  . Finally, the count rate, Nout(τ)
. Finally, the count rate, Nout(τ)  |Eout(z, τ)|2, of γ-photons shaped by the vibrating resonant absorber has the form
|Eout(z, τ)|2, of γ-photons shaped by the vibrating resonant absorber has the form

where Te ≡ 2δeL is the non-resonant absorber optical thickness. It is worthwhile to point out here that, because |Eout(z, τ)|2 = |Eout(z′, τ)|2, the waveform of a photon, Nout(τ)  |Eout(z, τ)|2, in the laboratory reference frame is the same as in the reference frame of the vibrating absorber.
|Eout(z, τ)|2, in the laboratory reference frame is the same as in the reference frame of the vibrating absorber.
In general, the output γ-radiation constitutes an amplitude- and frequency-modulated signal that has a form determined by the number of produced spectral components (that is, the modulation index), as well as their relative amplitudes and phases. If the p < 2.4 (p = 2.4 is the first zero of J0(p)), then all Bessel functions Jn(p) of non-negative order are positive and the lower-frequency sidebands of the incident γ-photons in the vibrating reference frame (the first sum in equation (4)) are phase-matched with the phase difference between each neighbouring pair equal to  , whereas the upper-frequency sidebands (the second sum in equation (4)) are phase-matched with the phase difference between each neighbouring pair equal to
, whereas the upper-frequency sidebands (the second sum in equation (4)) are phase-matched with the phase difference between each neighbouring pair equal to  . This is illustrated in Fig. 3a for p = 1.8 (which is the position of the global maximum of J1(p)), corresponding to production of three upper and three lower sidebands, and
. This is illustrated in Fig. 3a for p = 1.8 (which is the position of the global maximum of J1(p)), corresponding to production of three upper and three lower sidebands, and  = 0. The phases of three upper-frequency sidebands and three lower-frequency sidebands are marked by brown squares and green triangles, respectively (see the right-hand vertical axis for the values of these phases). An elimination of either the ‘+1’ sideband or the ‘−1’ sideband from the incident spectrum (in the vibrating frame of reference, (equation (4))) by its tuning to the absorber resonance via the Doppler shift, caused by a constant velocity of the source relative to the absorber, leads to phase-matching of five out of the six remaining spectral components and results in the formation of pronounced ultrashort γ-ray pulses (see Figs 3b and 4 and Extended Data Figs 1 and 5). The theoretical curves on these figures are plotted in accordance with the numerical solutions of equation (11), (13) and (14), as well as the analytical formula in equation (15). To fit the experimental data in Figs 3 and 4, the calculated time dependencies were averaged over the acquisition intervals Ωdt = π/2 (Fig. 3b) and Ωdt = π/8 (Fig. 3c), determined by the experimental set-up. As is seen from Extended Data Fig. 1, the value of modulation index chosen for our experiment maximizes both the amplitude and the contrast of the produced pulses (red solid line). This happens because p = 1.8 corresponds to the global maximum of Bessel function J1(p), which determines the amplitude of the ‘−1’ sideband (in the vibrating reference frame), suppressed by the resonant absorber. Strengthening the spectrally selective impact of the absorber on the incident γ-photon in the vibrating reference frame leads to deeper modulation of the output photon in the laboratory frame of reference. As a result, reaching the peak of J1(p) corresponds to forming the most pronounced pulses. Reduction of the modulation index to p = 0.8 leads to a decrease in the contrast of the produced pulses because of the narrowing of the generated spectrum (blue dashed line in Extended Data Fig. 1). With an increase in modulation index, larger numbers of sidebands are produced, but because tuning the single absorber resonance allows for the elimination of only one ‘wrong phase’ spectral component (either ‘+1’ or ‘−1’), it becomes impossible to phase match all of them using a single absorber line. Thus, an increase in modulation index above the optimal value (an example corresponding to p = 2.8 is shown in Extended Data Fig. 1 by the green dashed line) leads to a reduction in the pulse contrast and generation of additional spikes because of the growing influence of the phase-mismatched spectral components.
= 0. The phases of three upper-frequency sidebands and three lower-frequency sidebands are marked by brown squares and green triangles, respectively (see the right-hand vertical axis for the values of these phases). An elimination of either the ‘+1’ sideband or the ‘−1’ sideband from the incident spectrum (in the vibrating frame of reference, (equation (4))) by its tuning to the absorber resonance via the Doppler shift, caused by a constant velocity of the source relative to the absorber, leads to phase-matching of five out of the six remaining spectral components and results in the formation of pronounced ultrashort γ-ray pulses (see Figs 3b and 4 and Extended Data Figs 1 and 5). The theoretical curves on these figures are plotted in accordance with the numerical solutions of equation (11), (13) and (14), as well as the analytical formula in equation (15). To fit the experimental data in Figs 3 and 4, the calculated time dependencies were averaged over the acquisition intervals Ωdt = π/2 (Fig. 3b) and Ωdt = π/8 (Fig. 3c), determined by the experimental set-up. As is seen from Extended Data Fig. 1, the value of modulation index chosen for our experiment maximizes both the amplitude and the contrast of the produced pulses (red solid line). This happens because p = 1.8 corresponds to the global maximum of Bessel function J1(p), which determines the amplitude of the ‘−1’ sideband (in the vibrating reference frame), suppressed by the resonant absorber. Strengthening the spectrally selective impact of the absorber on the incident γ-photon in the vibrating reference frame leads to deeper modulation of the output photon in the laboratory frame of reference. As a result, reaching the peak of J1(p) corresponds to forming the most pronounced pulses. Reduction of the modulation index to p = 0.8 leads to a decrease in the contrast of the produced pulses because of the narrowing of the generated spectrum (blue dashed line in Extended Data Fig. 1). With an increase in modulation index, larger numbers of sidebands are produced, but because tuning the single absorber resonance allows for the elimination of only one ‘wrong phase’ spectral component (either ‘+1’ or ‘−1’), it becomes impossible to phase match all of them using a single absorber line. Thus, an increase in modulation index above the optimal value (an example corresponding to p = 2.8 is shown in Extended Data Fig. 1 by the green dashed line) leads to a reduction in the pulse contrast and generation of additional spikes because of the growing influence of the phase-mismatched spectral components.
The waveform of an output γ-photon (equation (11)) strongly depends on detuning the central frequency of the source, ωr, from the resonance frequency of the absorber, ωa. The detuning, ωr − ωa, determines which component of the incident spectrum (in the vibrating reference frame) is affected by the absorber resonance (attenuated and/or phase-shifted owing to the resonant dispersion), and how the output spectrum is related to the incident spectrum. The time dependences of a γ-photon count rate, plotted for three different values of detuning, ωr − ωa = 0.5Ω, ωr − ωa = Ω and ωr − ωa = 2Ω, corresponding to tuning the absorber resonance into the middle between the ‘0’ and ‘−1’ sidebands, to the ‘−1’ sideband and to the ‘−2 sideband, respectively, are plotted in Extended Data Fig. 2. As is seen from that figure, only tuning the ‘−1’ sideband to the absorber resonance (as in our experiment; see Figs 3a, b and 4) leads to formation of the ultrashort γ-radiation pulses owing to elimination of the ‘wrong-phase’ spectral component (red solid line). Tuning the ‘−2’ sideband to the resonance leads to the less pronounced amplitude modulation of the output γ-photon, caused by elimination of the ‘right-phase’ component (green dashed line). In turn, tuning the absorber resonance between the sidebands leads to the weakest amplitude modulation (shown by blue dashed line) because of the limited influence of the absorber resonance on the spectrum of the incident γ-photon.
Although using higher values of the modulation index does not allow for an increase in the peak amplitude or a reduction in pulse duration, it does allow for efficient single-photon shaping (Fig. 3c), demonstrating spitting of the single γ-photon into two pulses. The time interval between the pulses and their relative amplitudes can be controlled by variation of the vibration phase,  , as shown in Extended Data Fig. 3.
, as shown in Extended Data Fig. 3.
As is seen in Extended Data Fig. 3, a change in the vibration phase at the moment of formation of the excited state |b〉 of the radiating nucleus (Fig. 1a) leads to a shift in the modulation pattern, produced as a result of the absorber’s vibration, with respect to the front edge of the photon. Accordingly, it leads to a time shift of the second pulse (generated inside the absorber) in the produced pulse pair relative to the first pulse (which is the Brillouin precursor). In the case of Fig. 3c and Extended Data Fig. 3, the vibration period, 2π/Ω = 385 ns, considerably exceeds the lifetime of the incident photon Tr = 141 ns, and a change in the vibration phase therefore strongly affects the output photon waveform. If the oscillation cycle is shorter than the incident photon lifetime, as in the case of Fig. 3a, b, where 2π/Ω = 98 ns, the vibration phase has a minor role (see Fig. 3b and its inset).
The output photon waveform also depends on the frequency of vibration, Ω, which determines the timescale of the beatings in the photon detection probability (or the intensity of the output radiation) produced as a result of the absorber’s vibration. This dependence is illustrated in Extended Data Fig. 4, where the output count rate is plotted for the parameters of the experiment on a double-pulse formation (Fig. 3c) and three different values of the vibration frequency: Ω/2π = 1.3 MHz (green dashed line), 2.6 MHz (the same as in Fig. 3c (red solid line)) and 5.2 MHz (blue dashed line). As is seen from Extended Data Fig. 4, an increase in the vibration frequency corresponds to a shrinking of the modulation structure in time, whereas a decrease in the frequency of vibration leads to a stretching of the modulation pattern in time.
It follows from Extended Data Figs 3 and 4 that the parameter values that were chosen for the experiment on double-pulse (time-bin qubit) formation from an incident γ-photon (Fig. 3c), that is, Ω/2π = 2.6 MHz and  are optimal for the generation of the two well-separated pulses of nearly the same amplitude.
are optimal for the generation of the two well-separated pulses of nearly the same amplitude.
So far, we have considered the single-photon waveforms described by equation (11). Averaging the output photon count rate, Nout(τ) = Nout(t − t0), over the moment t0 gives the time-dependence of the full flow of γ-photons, or an intensity of the continuous γ-radiation, which can be produced by a high-activity source:

The substitution of equation (11) into equation (12) results in

where Bnm = Bmn and ϕnm = ϕmn are real parameters defined by the relation

Under the approximation of complete suppression of a single ‘+1’ or ‘−1’ spectral component of the incident photon (in the vibrating frame of reference), and in the absence of the influence of the resonant absorber on all the other sidebands, equation (13) takes a very simple form:

Noting that cos(Ωt + π) = −cos(Ωt) and sin(Ωt + π) = −sin(Ωt), it is clearly seen from equation (15) that tuning the absorber line to the opposite sideband is equivalent to a change in the phase of vibration by π. If t0, the moment of formation of the excited state |b〉 of the radiating nucleus, is undefined, this is equivalent to shifting the starting observation time, which can be chosen arbitrarily, and does not change the intensity envelope. However, in the case of a single-photon waveform, both t0 and  are fixed by the instant of formation of the excited nuclear state (emitting the photon). Therefore, the photons ‘born’ in different vibration phases can have qualitatively different waveforms, as shown in Fig. 3c, its inset and Extended Data Fig. 3. Equation (15) also shows that the peak amplitude of the produced pulses is given by
are fixed by the instant of formation of the excited nuclear state (emitting the photon). Therefore, the photons ‘born’ in different vibration phases can have qualitatively different waveforms, as shown in Fig. 3c, its inset and Extended Data Fig. 3. Equation (15) also shows that the peak amplitude of the produced pulses is given by  . Thus, the pulses indeed reach their maximum intensity when the corresponding Bessel functions,
. Thus, the pulses indeed reach their maximum intensity when the corresponding Bessel functions,  , take their peak value,
, take their peak value,  , that is, at p = 1.8.
, that is, at p = 1.8.
Although equation (15) does not account for the finite spectral width of both the absorber resonance and the incident γ-radiation (that is, the width of each sideband of the incident spectrum in the absorber reference frame), in the case of high vibration frequency (relative to the source (and absorber) linewidth) it is in good qualitative as well as quantitative agreement with the experimental results (Extended Data Fig. 5).
As demonstrated in this work, the harmonic vibrations (with frequencies in the range of 1–10 MHz and modulation index ranging from 1 to 7) of the single stainless-steel absorber (with a natural abundance of 57Fe and an optical thickness of about 5) makes it possible to form ultrashort pulses with a duration an order of magnitude shorter than the lifetime of the upper nuclear level (141 ns) as well as to produce a variety of waveforms from a single γ-photon (including a decaying train of ultrashort pulses, a double pulse and a single triangular pulse) by changing the vibration frequency, the modulation index, the vibration phase at the moment of the photon’s arrival, and the detuning of the incident photon from the absorber resonance.
The range of possibilities for γ-photon shaping and ultrashort pulse production based on modulation of the nuclear transition frequency may be essentially extended by using both single and multiple absorbers of larger optical thicknesses (enriched with 57Fe), as well as absorbers with a split transition line; different Mössbauer isotopes (in particular 67Zn, which possesses a 93.3-keV recoilless transition with a 12.2-kHz linewidth); higher modulation frequencies and modulation indices; anharmonic (and even aperiodic) vibrations; and other techniques (such as the Zeeman effect) for modulation of the nuclear transition frequency. These possibilities will be addressed in our future studies.
References
Shwartz, S. et al. X-ray parametric down-conversion in the Langevin regime. Phys. Rev. Lett. 109, 013602 (2012)
Röhlsberger, R., Wille, H.-C., Schlage, K. & Sahoo, B. Electromagnetically induced transparency with resonant nuclei in a cavity. Nature 482, 199–203 (2012)
Röhlsberger, R., Schlage, K., Sahoo, B., Couet, S. & Rüffer, R. Collective Lamb shift in single-photon superradiance. Science 328, 1248–1251 (2010)
Heeg, K. P. et al. Vacuum-assisted generation and control of atomic coherences at x-ray energies. Phys. Rev. Lett. 111, 073601 (2013)
Shakhmuratov, R., Vagizov, F. & Kocharovskaya, O. Single γ-photon revival and radiation burst in a sandwich absorber. Phys. Rev. A 87, 013807 (2013)
Liao, W.-T., Pálffy, A. & Keitel, C. H. Coherent storage and phase modulation of single hard-X-ray photons using nuclear excitons. Phys. Rev. Lett. 109, 197403 (2012)
Liao, W.-T., Pálffy, A. & Keitel, C. H. Nuclear coherent population transfer with X-ray laser pulses. Phys. Lett. B 705, 134–138 (2011)
Adams, B. W. et al. X-ray quantum optics. J. Mod. Opt. 60, 2–21 (2013)
Ma, X.-S. et al. Quantum teleportation over 143 kilometres using active feed-forward. Nature 489, 269–273 (2012)
Döring, F. et al. Sub-5 nm hard X-ray point focusing by a combined Kirkpatrick-Baez mirror and multilayer zone plate. Opt. Express 21, 19311–19323 (2013)
Hammerer, K., Sørensen, A. S. & Polzik, E. S. Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 82, 1041–1093 (2010)
Hoy, G. R., Hamill, D. W. & Wintersteiner, P. P. in Mössbauer Effect Methodology Vol. 6 (ed. Gruverman, I. J. ) 109–121 (Plenum, 1970)
Amann, J. et al. Demonstration of self-seeding in a hard-X-ray free-electron laser. Nature Photon. 6, 693–698 (2012)
Shvyd’ko, Stoupin, S., Blank, V. & Terentyev, S. Near-100% Bragg reflectivity of X-rays. Nature Photon. 5, 539–542 (2011)
Antonov, V. A., Radeonychev, Y. V. & Kocharovskaya, O. Formation of a single attosecond pulse via interaction of resonant radiation with a strongly perturbed atomic transition. Phys. Rev. Lett. 110, 213903 (2013)
Helistö, P., Tittonen, I. & Katila, T. Enhanced transient effects due to saturated absorption of recoilless γ-radiation. Phys. Rev. B 34, 3458–3461 (1986)
Smirnov, G. V. & Potzel, W. Perturbation of nuclear excitons by ultrasound. Hyperfine Interact. 123/124, 633–663 (1999)
Kuznetsova, E., Kolesov, R. & Kocharovskaya, O. Compression of γ-ray photons into ultrashort pulses. Phys. Rev. A 68, 043825 (2003)
Smirnov, G. V. General properties of nuclear resonant scattering. Hyperfine Interact. 123/124, 31–77 (1999)
Kagan Theory of coherent phenomena and fundamentals in nuclear resonant scattering. Hyperfine Interact. 123/124, 83–126 (1999)
Hannon, J. P. & Trammell, G. T. Coherent gamma-ray optics. Hyperfine Interact. 123/124, 127–274 (1999)
Kolchin, P., Belthangady, C., Du, S., Yin, G. Y. & Harris, S. E. Electro-optic modulation of single photons. Phys. Rev. Lett. 101, 103601 (2008)
Pittman, T. It’s a good time for time-bin qubits. Physics 6, 110 (2013)
Röhlsberger, R. Nuclear Condensed Matter Physics using Synchrotron Radiation (Springer Tracts Mod. Phys. 208, Springer, 2005)
Radeonychev, Y. V., Tokman, M. D., Litvak, A. G. & Kocharovskaya, O. Acoustically induced transparency in optically dense resonance medium. Phys. Rev. Lett. 96, 093602 (2006)
Kocharovskaya, O. A. & Khanin, Ya. I. Population trapping and coherent bleaching of a three-level medium by a periodic train of ultrashort pulses. Sov. Phys. JETP 63, 945–949 (1986)
Harris, S. E. Electromagnetically induced transparency. Phys. Today 50, 36–42 (1997)
Fleischhauer, M., Imamoğlu, A. & Marangos, J. P. Electromagnetically induced transparency: optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005)
Lvovsky, A. I., Sanders, B. C. & Tittel, W. Optical quantum memory. Nature Photon. 3, 706–714 (2009)
Simon, C. et al. Quantum memories. Eur. Phys. J. D 58, 1–22 (2010)
Acknowledgements
We acknowledge the support from the US NSF (grant no. PHY-1307346), the RFBR (grants nos 13-02-00831 and 12-02-00263) and The Ministry of Education and Science of the Russian Federation (contract no. 11.G34.31.0011). V.A. acknowledges support from the Dynasty Foundation.
Author information
Authors and Affiliations
Contributions
F.V. developed the experimental methods, designed the experiment and derived all the experimental results. V.A., Y.V.R. and R.N.S. developed the theoretical description. V.A. and F.V. determined the optimal parameters for the experiments and provided the theoretical fit to experimental data. Y.V.R. and F.V. suggested the technique for observing the single-photon waveforms. R.N.S. obtained analytical solutions for some limiting cases. O.K. suggested the idea, coordinated the efforts and wrote the paper. All authors discussed the results and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Time dependences of a γ-photon detection probability for different values of modulation index.
The values of modulation index are p = 0.8 (blue dashed line), p = 1.8 (red solid line) and p = 2.8 (green dashed line). All the other parameters are the same as in our experiment (Fig. 3).
Extended Data Figure 2 Time dependences of a γ-photon detection probability for different detunings of the central frequency of the source, ωr, from the resonance frequency of the absorber, ωa.
The values of detuning are ωr − ωa = 0.5Ω (blue dashed line), ωr − ωa = Ω (red solid line) and ωr − ωa = 2Ω (green dashed line). All the other parameters are the same as in our experiment (Fig. 3).
Extended Data Figure 3 Variation of the waveform of a 14.4-keV γ-photon with a change in the vibration phase, 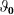 , at the moment of detection of the preceding 122-keV γ-photon.
, at the moment of detection of the preceding 122-keV γ-photon.
The parameter values are the same as in Fig. 3c, corresponding to double-pulse formation, except for the initial phases of vibration, which are as follows:  , the same as in Fig. 3c (red solid line),
, the same as in Fig. 3c (red solid line),  (blue dashed line),
(blue dashed line),  (the same as in the inset of Fig. 3c (green dashed line)) and
(the same as in the inset of Fig. 3c (green dashed line)) and  (cyan dashed line).
(cyan dashed line).
Extended Data Figure 5 Count rate of 14.4-keV photons versus time for the case of Fig. 4.
The blue dots centred at the confidence intervals correspond to the experimental data, and the red and green solid curves are plotted according to equations (13) and (14) and, respectively, equation (15).
Rights and permissions
About this article
Cite this article
Vagizov, F., Antonov, V., Radeonychev, Y. et al. Coherent control of the waveforms of recoilless γ-ray photons. Nature 508, 80–83 (2014). https://doi.org/10.1038/nature13018
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature13018
This article is cited by
-
Measurement of the sub-nanometer vibration amplitudes using 57Fe synchrotron Mössbauer source
Interactions (2024)
-
Optimal Motion Law of a Resonant Nuclear Absorber for the Formation of Short Pulses of Mössbauer Radiation
Radiophysics and Quantum Electronics (2023)
-
Slowing down x-ray photons in a vibrating recoilless resonant absorber
Scientific Reports (2022)
-
Reply to: On yoctosecond science
Nature (2022)
-
Nonlinearity-mediated digitization and amplification in electromechanical phonon-cavity systems
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.





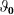 , at the moment of detection of the preceding 122-keV γ-photon.
, at the moment of detection of the preceding 122-keV γ-photon.