Main

The Heisenberg uncertainty principle is perhaps one of the most curious and surprising features of quantum physics: it prohibits certain properties of physical systems (for example the position and momentum of a single particle) from being simultaneously well defined1. Such incompatibility of properties, however, contrasts strongly with what we experience in our everyday lives. If we look at a globe of the Earth, we can see only one hemisphere at any given time, but we suppose that the shapes of the continents on the far side remain the same irrespective of the observer’s vantage point. Thus, by spinning the globe around to view different continents, we are able to construct a meaningful picture of the whole. It is reasonable to assume that observation reveals features of the continents that are present independent of which other continent we might be looking at. In an analogous way, classical physics allows us to assign properties to a system without actually measuring it. All these properties can be assumed to exist in a consistent way, whether or not they are measured.

The world view in which system properties are defined independently of both their own measurement and what other measurements are made is called non-contextual realism. From this viewpoint, mathematically speaking there must be a joint probability distribution for these properties, defining the outcome probabilities for an experiment in which they are observed (if a joint probability distribution exists, rolling appropriately weighted dice would reproduce all behaviour of such an experiment). The reverse is not necessarily true. Nature could in principle be such that although joint probability distributions exist they do not relate to properties of a system.

To derive the Bell-like inequality in ref. 19, consider five numbers, a1, a2, a3, a4 and a5, each equal to +1 or −1. For any choice of them, the following algebraic inequality is true:

Let these numbers now be the results of five corresponding two-outcome measurements, A1, A2, A3, A4 and A5. Then, assuming that there exists a joint probability distribution for the 25 possible measurement outcome combinations, taking the average of inequality (1) gives (see Supplementary Information, section 1)

Here, angle brackets denote averages of measurement outcomes and not quantum mechanical expectation values.

We would like to emphasize that, given only the result of inequality (2), an experimental violation of this inequality precludes the description of the measurement results using a joint probability distribution. The same form of argument can be used to show that such a violation also precludes the existence of any non-contextual realistic model for the results.

The above inequality can be tested experimentally if we assume that a long series of individual experimental runs would result in a fair sampling of a joint probability distribution (if one were to exist). Our experimental implementation consists of five main stages, depicted in Fig. 1b–f. We prepare single photons, each distributed among three modes (Fig. 1a) monitored by detectors. At each stage, the two outcomes of a given measurement are defined by determining whether the corresponding detector clicked. For example, at stage one (Fig. 1b), the outcomes of measurement A1 are given by the response of the upper detector, and we assign numbers to the outcomes as above: that is, A1 = −1 if the detector clicked and A1 = +1 if it did not. Similarly, the outcomes of measurement A2 are given by the response of the lower detector. By measuring A1 and A2 together for a number of photons, we obtain the average value 〈A1A2〉, the first term of inequality (2).

Figure 1: Experimental preparation and five successive measurement stages.
figure 1

Straight, black lines represent the optical modes (beams) and grey boxes represent transformations on the optical modes. a, Single photons are distributed among three modes by transformations TA and TB. This preparation stage is followed by one of the five measurement stages. b–f, At each stage, the response of two detectors monitoring the optical modes defines one of the pairs of measurements in inequality (2). Outcomes of the measurements are defined by determining whether the corresponding detector clicks. If a detector clicks then a value of −1 is assigned to the corresponding measurement; otherwise, a value of +1 is assigned. A key aspect of our experimental implementation is that each transformation acts only on two modes, leaving the other mode completely unaffected. Thus, the part of the physical set-up corresponding to measurement A2 is exactly the same in b and c (likewise, A3 is the same in c and d, and so on). We note that this set-up can also be arranged such that the choice between A1 and A3 is made long after A2 is measured. Thus, it seems reasonable to assume that measurement A2 is independent of whether it is measured together with A1 or A3. The same reasoning can be applied to measurements A3, A4 and A5.

PowerPoint slide

Full size image

To move to the second stage, we perform a transformation, T1, on the two upper modes (Fig. 1c). Because the mode monitored by the lower detector is not affected by T1, this detector still measures the outcome of A2. The upper detector, however, defines a different measurement—we call it A3. Most significantly, for any specific run of the experiment it seems reasonable to assume that whether or not detector A2 clicks must be independent of whether or not we apply the transformation to the other two modes. In the remaining three stages, we apply three more transformations, each time changing one measurement and leaving the other unaffected.

The last transformation, T4, is chosen such that the new measurement should be equivalent to the original measurement of A1. Unlike for the other measurements; however, this new measurement apparatus (Fig. 1f) is not physically the same as the one measuring A1 in Fig. 1b. We therefore call the sixth measurement and derive the following new inequality to replace inequality (2) (Supplementary Information, section 2):

Here and we note that for the ideal case of , this extended inequality reduces to inequality (2).

Measurements A1 and occur at different stages of the experiment, so the expectation value cannot be calculated in the same way as the other terms. Instead, we note that in the ideal case, whenever detector A1 fires, must also fire, and vice versa. Therefore, if the upper beam is blocked where A1 would be measured, then should never click. Likewise, blocking the other two modes should not change the count rate at detector . Therefore, we can rewrite as

with the conditional probabilities experimentally accessible by blocking and monitoring the appropriate modes (Supplementary Fig. 1). The extra term, ε, in inequality (3) therefore completely accounts for any differences between A1 and . It is an open question whether any experimental apparatus can be designed where A1 and are physically the same.

In our measurements, we find that ε = 0.081(2), thus bounding the left-hand side of inequality (3) by −3.081(2), and that the terms on the left-hand side are each less than −0.7 adding up to give −3.893(6). This represents a violation of inequality (3) by more than 120 standard deviations, demonstrating that no joint probability distribution is capable of describing our results. The violation also excludes any non-contextual hidden-variable model. The result does, however, agree well with quantum mechanical predictions, as we will show now.

A single photon distributed among three modes can be described by the mathematical formalism used for spin-one particles. Using this formalism, the measurements performed in our experiment can be expressed by spin operators as , where is a spin projection onto the direction in real three-dimensional space. Two measurements and are compatible if and only if the directions and are orthogonal. Thus, the five measurement directions have to be pairwise orthogonal to make the measurements themselves pairwise compatible (Fig. 2). In our experiment, we have three modes which by design represent orthogonal states. These can be seen as orthogonal directions in the spin case. An essential feature of a spin-one system is that out of three projections squared onto three orthogonal directions, exactly two are equal to 1 and the remaining one must be equal to 0. Correspondingly, a single photon distributed among three different modes will cause a click in exactly one detector only and none in the other two.

Figure 2: Representation of the measurements and a state providing maximal violation of the inequality (2) by directions in three-dimensional space19.
figure 2

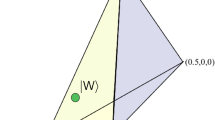
The measurement directions are labelled by the measurements Ai (i = 1, 2, …, 5). They are given as , where is a spin projection onto the direction . The five measurement directions are pairwise orthogonal, making the measurements Ai pairwise compatible. These five pairs correspond to the five measurement devices from Fig. 1b–f. For a maximal violation, the directions form a regular pentagram and the input state Ψ0 has zero spin along the symmetry axis of the pentagram.

PowerPoint slide

Full size image

For the maximal violation of inequalities (2) and (3), the five directions form a regular pentagram and the input state has zero spin along the symmetry axis of the pentagram19. In the ideal case, that is, when (ε = 0), if the optimal state is taken quantum mechanics predicts the value of the left-hand side of inequality (3) to be 5 − 4 ≈ −3.944. Smaller violations are also predicted for a range of non-ideal pentagrams and other input states. In our case, the departure from the maximum achievable violation can be attributed to residual errors in the settings of experimental parameters (Supplementary Information, section 5).

The five pairs of compatible measurements correspond to the five measurement devices described in Fig. 1b–f. Spin rotations, necessary to switch between various measurement bases, can be realized by combining the optical modes, for example on a tunable beam splitter. Each rotation of a measurement basis leaves one of the axes unaffected because only two modes are combined and one is untouched. Operationally, the measurements at each stage are compatible (co-measurable) because they are defined by independent detectors.

We realize the above scheme using heralded, single, 810-nm photons. In the type-II collinear spontaneous parametric down-conversion in a nonlinear crystal, pairs of orthogonally polarized photons are produced in a polarization product state. We separate them at a polarizing beam splitter, with detection of a vertically polarized photon heralding the horizontally polarized photon in the measurement set-up. In practice, therefore, we record pairwise coincidences between the heralding detector and any one of the three detectors in the measurement apparatus (heralded single clicks).

To realize a three-state system, our photons propagate in three modes. Two of the three modes are realized as two polarizations of a single spatial mode. Conveniently, two-mode transformations can then be implemented using half-wave plates acting on the two polarization modes propagating in the same spatial mode. Different spatial modes are combined using calcite crystals (acting as polarizing beam splitters). Thus, we are able to apply transformations to any pair of modes (Fig. 3).

Figure 3: Experimental set-up.
figure 3

a, Preparation of the required single-photon state. About 3 mW of power from a grating-stabilized laser diode (LD) at a wavelength of 405 nm is used to pump the nonlinear crystal (20 mm long, periodically poled potassium titanyl phosphate (ppKTP)), producing pairs of orthogonally polarized photons by means of spontaneous parametric down-conversion. The pump is filtered out with the help of a combination of dichroic mirrors and interference filters (labelled jointly as F). The photon pairs are split up at a polarizing beam splitter (PBS). Detection of the reflected photon heralds the transmitted one. Half-wave plates WPA and WPB transform the transmitted photon into the desired three-mode state. Calcite polarizing beam splitters separate and combine orthogonally polarized modes. b, In the measurement apparatus, half-wave plates WP1 to WP4 realize the transformations T1 to T4 on pairs of modes (wave-plate orientations are listed in Supplementary Table 1). Each transformation can be ‘turned off’ by setting the optical axis of the corresponding wave plate vertically (at 0°). The unlabelled (light blue) wave plates serve to balance the path lengths and to switch between horizontal and vertical polarization (the second unlabelled wave plate is set to 0°; the rest are set to 45°). Detecting heralded single photons in practice means registering coincidences between single-photon detectors: D0 and each of D1, D2 and D3. Registrations in two of the detectors D1, D2 and D3 give the values Ai necessary to evaluate the inequality (Table 1). The third detector is used to identify the trials when the photon is lost. We note that the assignment of measurements to detectors in the experimental set-up differs in some cases from that described in the simplified conceptual scheme (Fig. 1). We use home-built avalanche photodiode single-photon detectors and coincidence logic. The effective coincidence window (including the jitter of the detector) is about 2.3 ns.

PowerPoint slide

Full size image

The experiment consists in total of seven stages. The first five stages (corresponding to the five left-hand terms of inequality (3)) are the measurement configurations illustrated in Fig. 1b–f, whereas the final two, depicted in Supplementary Fig. 1, give us the value of ε. All of these measurements are realized with a single experimental apparatus tuned to one of seven configurations. Configurations one to five differ in the number of transformations that are ‘active’. We activate and deactivate the transformations by changing the orientation of wave plates (see Supplementary Table 1 for the specific settings). For the two measurements in the final stage, where we measure conditional probabilities by blocking the appropriate modes (Supplementary Fig. 1), we insert a polarizer in two orthogonal orientations between wave plates WPB and WP1 (Fig. 3).

For each measurement, we record clicks for 1 s, registering about 3,500 heralded single photons. We repeat each stage 20 times, average the results and calculate the standard deviation of the mean to estimate the standard uncertainties which we then propagate to the final results (Table 1). Owing to photon loss, sometimes no photon is detected in the measurement, despite the observation of a heralding event. We therefore discard all events for which only the trigger detector (D0) and none of the measurement detectors (D1, D2 and D3) fire. We assume that the photons we do detect are a representative sample of all created photons (fair-sampling assumption).

Table 1 Collected experimental results
Full size table

A key aspect of Kochen–Specker experiments is that the co-measured observables must commute; if they do not, the ‘compatibility loophole’20 is potentially opened. The construction of the measurements in our experiment enforces their compatibility and thus makes the experiment immune to the compatibility loophole. Detector efficiencies and losses in the set-up prevent us from closing the detection loophole. Instead, we assume that the statistics of unregistered events would have been the same as the statistics of observed ones.

Our experimental results are in conflict with any description of nature that relies on a joint probability distribution of outcomes of a simple set of measurements. This also precludes any description in terms of non-contextual hidden-variable models. To our knowledge, this is the first observation of such a conflict for a single three-state system, which, apart from being the most basic one where such a contradiction is possible, cannot even in principle contain entanglement. For such a system, inequality (2) involves the smallest number of measurements possible.

Our result sheds new light on the conflict between quantum and classical physics. To finish, we want to point out that any model based on a joint probability distribution can in principle be non-deterministic. The experimental preclusion of such models highlights the fact that even for a single, indivisible quantum system, allowing randomness is not sufficient to allow its description with a conceptually classical model.