Main

The formation of normal ripple patterns is driven by the 'separation zones' (regions with reversed flow) created in the troughs between ripple crests1,2. The wavelength of the ripples is set by the size of these zones, which is roughly proportional to the amplitude of the fluid oscillations and is independent of the frequency3,4,5. For a typical driving of amplitude 2.8 cm and frequency 0.5 Hz, for example, a ripple pattern with wavelength close to 4.0 cm is formed.

To investigate ripple patterns, we placed a thick layer of sand (spherical glass beads of diameter 250–350 μm) on a 0.6 m × 1 m tray inside a large, closed, stationary water tank with a transparent top lid, and pulled the tray back and forth sinusoidally. We started with completely regular patterns formed by pressing down a mould in the flat bed and then running the system (for a short time) with an amplitude 'commensurate' with the imprinted ripple wavelength.

We 'frustrated' these perfect patterns by suddenly changing the amplitude or frequency of the oscillations. When these changes are not too large, periodic ripple patterns are stable. For example, for a frequency of 0.67 Hz, ripples of wavelength 4.2 cm are stable for driving amplitudes between 2.4 and 3.4 cm. But when the driving amplitude or frequency is quenched beyond some threshold, three distinct short-wavelength instabilities occur.

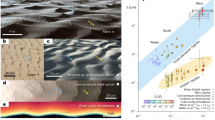
First, if the driving amplitude is increased sufficiently, the ripple crests distort along and transverse to the original ripples, and the pattern of compressed and 'bulging' regions forms a checkerboard tilted by 45° (Fig. 1a). As the deformations grow, dislocations occur until finally a new periodic ripple pattern with a larger wavelength is formed. Second, if the transition is reversed by decreasing the amplitude sufficiently, the pattern 'doubles' through the generation of small ripples between each of the original ones (Fig. 1b). Here, the separation zones become so small that they do not reach the troughs between the ripples. After the doubling, the wavelength of the system is then too small and the final state is reached through a bulging instability. Third, if the driving frequency is increased sufficiently, the ripples become unstable to the formation of stationary 'pearls' in the troughs between the ripples, which again form a tilted pattern (Fig. 1c). Unlike bulging and doubling, pearling saturates and disappears reversibly when the frequency is decreased.

Figure 1: Patterns obtained by changing the driving parameters for a tray of sand oscillating in a water tank.
figure 1

a, b, Sequences of pictures from two experiments in which the amplitude of the drive was changed. The tray area in each is 53 cm × 53 cm; the light source was on the left and the sand tray was oscillated in the left-right direction; the camera was directly above the sand bed. Below each picture is shown the central region of the corresponding power spectrum, 2.32 m−1 × 1.16 m−1. Numbers in the corners show the period at which the pictures were taken. For the top row (a), the initial wavelength was 4.2 cm, then the amplitude was 4.0 cm and the frequency 0.41 Hz. The power spectrum shows clear evidence of the bulging modulations mentioned in the text. For the bottom row (b), the imprinted wavelength was 5.6 cm, the driving amplitude was 2.8 cm and the frequency 0.68 Hz. The initial doubling is evident. c, The pearling transition and the corresponding power spectra in the range 1.88 m−1 × 0.94 m−1. Each picture shows an area of 43 cm × 53 cm. The ripples have a wavelength of 4.2 cm; the driving amplitude was 2.8 cm; frequencies (f) are indicated. Top, state well below the transition; bottom, fully developed pearling state. The pearls are new small ripples and not distortions of old ripples, because only the troughs and not the crests are deformed. Both states are stable at their respective driving parameters, so no period number is shown.

Full size image

Although our system superficially resembles other classic pattern-forming systems6 such as Rayleigh–Bénard convection, the transition scenarios described here have not been seen before. We believe that the theory of these instabilities must start with the separation zones, which have the shape of cylindrical vortices along the ripple troughs. These might be prone to instabilities7 like the Rayleigh–Plateau 'sausage' instability (which may lead to bulging), or the centrifugal instability that gives rise to Taylor vortices whose axes are transverse to the cylinder (which may lead to pearling).