Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Double-quantum vortex in superfluid 3He-A

Nature volume 404, pages 471–473 (2000)Cite this article

Abstract

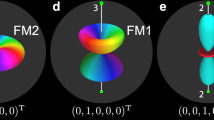
Linear defects are generic in continuous media1. In quantum systems they appear as topological line defects which are associated with a circulating persistent current. In relativistic quantum field theories they are known as cosmic strings2, in superconductors as quantized flux lines3, and in superfluids3,4 and low-density Bose–Einstein condensates5 as quantized vortex lines. A conventional quantized vortex line consists of a central core around which the phase of the order parameter winds by 2πn, while within the core the order parameter vanishes or is depleted from the bulk value. Usually vortices are singly quantized (that is, have n = 1). But it has been theoretically predicted that, in superfluid 3He-A, vortex lines are possible that have n = 2 and continuous structure, so that the orientation of the multi-component order parameter changes smoothly throughout the vortex while the amplitude remains constant. Here we report direct proof, based on high-resolution nuclear magnetic resonance measurements, that the most common vortex line in 3He-A has n = 2. One vortex line after another is observed to form in a regular periodic process, similar to a phase-slip in the Josephson effect.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Double-quantum vortex in superfluid 3He-A and its nuclear magnetic resonance signature.
Figure 2: Height of the vortex satellite peak in the NMR absorption spectrum, as a function of rotation velocity Ω.
Figure 3: Determination of the probability distribution for the interval ΔΩ which separates successive phase-slip events in periodic vortex formation.
Figure 4: Stable long-range periodicity of phase-slip process.

Similar content being viewed by others

References

  1. Kléman,M. Points, Lines, and Walls in Liquid Crystals, Magnetic Systems and Various Ordered Media (Wiley, New York, 1983).

    Google Scholar 

  2. Hindmarsh,M. & Kibble,T. W. B. Cosmic strings. Rep. Prog. Phys. 58, 477–562 (1995).

    Article  ADS  MathSciNet  Google Scholar 

  3. Tilley,D. R. & Tilley,J. Superfluidity and Superconductivity (IOP, New York, 1990).

    Google Scholar 

  4. Vollhardt,D. & Wölfle,P. The Superfluid Phases of 3He (Taylor & Francis, London, 1990).

    Book  Google Scholar 

  5. Matthews,M. R. et al. Vortices in a Bose–Einstein condensate. Phys. Rev. Lett. 83, 2498–2501 (1999).

    Article  ADS  CAS  Google Scholar 

  6. Onsager,L. Nuovo Cimento 6 (Suppl. 2), 249 ( 1949).

    Google Scholar 

  7. Feynman,R. P. Progress in Low Temperature Physics (ed. Gorter, C. G.) Vol. 1 , 17–51 (North-Holland, Amsterdam, 1955).

    Book  Google Scholar 

  8. Mermin,N. D. & Ho,T. L. Circulation and angular momentum in the A phase of superfluid helium-3. Phys. Rev. Lett. 36, 594–597 (1976).

    Article  ADS  CAS  Google Scholar 

  9. Ho,T. L. Spinor Bose condensates in optical traps. Phys. Rev. Lett. 81, 742–745 (1998).

    Article  ADS  CAS  Google Scholar 

  10. Achucarro,A. & Vachaspati,T. Semilocal and electroweak strings. Phys. Rep. (in the press); preprint hep-ph/9904229 at 〈xxx.lanl.gov〉 (1999).

  11. Anderson,P. W. & Toulouse,G. Phase slippage without vortex cores: Vortex textures in superfluid 3He. Phys. Rev. Lett. 38, 508–511 (1977).

    Article  ADS  CAS  Google Scholar 

  12. Volovik,G. E. & Kopnin,N. B. On rotating 3He-A. JETP Lett. 25, 22–24 (1977).

    ADS  Google Scholar 

  13. Hakonen,P. J., Ikkala,O. T. & Islander, S. T. Experiments on vortices in rotating superfluid 3He-A. Phys. Rev. Lett. 49, 1258 –1261 (1982).

    Article  ADS  CAS  Google Scholar 

  14. Seppälä,H. K. & Volovik,G. E. Evidence for nonsingular vorticity in the Helsinki experiments on rotating 3He. J. Low Temp. Phys. 51, 279– 290 (1983).

    Article  ADS  Google Scholar 

  15. Packard,R. E. The role of the Josephson-Anderson equation in superfluid helium. Rev. Mod. Phys. 70, 641–651 (1998).

    Article  ADS  CAS  Google Scholar 

  16. Ruutu,V. M. H., Parts, Ü., Koivuniemi,J. H., Kopnin,N. B. & Krusius, M. Intrinsic and extrinsic mechanisms of vortex formation in rotating superfluid 3He-B. J. Low Temp. Phys. 107, 93–164 ( 1997).

    Article  ADS  CAS  Google Scholar 

  17. Parts,Ü et al. Phase diagram of vortices in superfluid 3He-A. Phys. Rev. Lett. 75, 3320– 3323 (1995).

    Article  ADS  CAS  Google Scholar 

Download references

Acknowledgements

We thank H. Götz for help with the data analysis. This collaboration was carried out under the EU-TMR programme.

Author information

Authors and Affiliations

  1. Low Temperature Laboratory, Helsinki University of Technology, PO Box 2200, HUT, FIN-02015 , Finland

    R. Blaauwgeers, V. B. Eltsov, M. Krusius, J. J. Ruohio, R. Schanen & G. E. Volovik

  2. Kamerlingh Onnes Laboratory, Leiden University, PO Box 9504, Leiden , 2300 RA, The Netherlands

    R. Blaauwgeers

  3. Kapitza Institute for Physical Problems , Kosygina 2, Moscow, 117334, Russia

    V. B. Eltsov

  4. Centre de Recherches sur les Très Basses Températures, Centre National de la Recherche Scientifique, BP 166, Grenoble, F-38042 Cedex 09, France

    R. Schanen

  5. Landau Institute for Theoretical Physics, Kosygina 2, Moscow, 117334, Russia

    G. E. Volovik

Authors
  1. R. Blaauwgeers
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. B. Eltsov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Krusius
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. J. J. Ruohio
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. R. Schanen
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. G. E. Volovik
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. B. Eltsov.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Blaauwgeers, R., Eltsov, V., Krusius, M. et al. Double-quantum vortex in superfluid 3He-A. Nature 404, 471–473 (2000). https://doi.org/10.1038/35006583

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1038/35006583

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing