Introduction

Noncoding RNA (ncRNA) molecules are involved in various biological processes, such as catalytic and regulatory roles. To perform these functions, they need to form special tertiary structures. At present, the number of solved RNA tertiary structures are very limited and so many computational methods have been proposed to predict RNA tertiary structures1,2,3,4,5,6,7,8,9,10,11,12,13, such as, MANIP2, RNA2D3D3, FARNA5/FARFAR6, MC-Fold/MC-Sym7, iFoldRNA8, NAST9, BARNACLE10, ASSEMBLE11 and V-fold model12. Liang and Schlick13 evaluated the performance of these methods and found that most predictions have RMSD values larger than 6Å from experimental structures and for RNA molecules of larger size (50–130 nucleotides) the mean RMSD value is about 20 Å. Furthermore, most of these methods are not automated and need manual manipulations. Therefore, although a lot of efforts, current methods of RNA tertiary structure prediction suffer strong limitations: short chains and/or manual manipulation13. It is still a challenge for accurate, automated and fast prediction of tertiary structures of long RNA chains.

In this paper we provide a fast and automated method of building RNA tertiary structure based on secondary structure, 3dRNA. Since the organization of RNA structure is largely defined by topological constraints encoded at secondary structural level and tertiary contacts14, we build whole RNA tertiary structure from the smallest secondary elements (SSEs) by using a two-step procedure. We first assemble the SSEs into hairpins or duplexes and then into complete structure since the tertiary structures of hairpins and duplexes usually can be built with a high accuracy. In 3dRNA the SSEs are defined as base pair, hairpin loop, internal loop, bulge loop, pseudoknot loop and junction because we observed that the three-dimensional (3D) backbone conformations of the SSEs are similar even if their sequences are different and from different structural families (see Supplementary Fig. S1 online and discussions below). Thus, we have a larger sample space to select 3D conformations of the SSEs. Furthermore, the 3D conformations of the SSEs we extract from experimental structures also contain one more base pair at their 5′-end, which is superimposed on the 3′-end base pair of the preceding SSE during assembling process. This can easily solve the problem of proper assembling between loops and other parts and substantially avoid steric conflicts in the model built finally. We also use a network representation of the secondary structure to describe the locations and connectivity of the SSEs, which makes it easy to implement the assembling process automatically.

Results

We benchmarked our method in a dataset of 300 RNA molecules with sequence identity less than 0.75 and lengths from 12 to 101 nucleotides (nt) selected from the PDB database (http://www.rcsb.org/), including 115 duplexes (12–56 nt), 153 hairpins (10–63 nt) and 32 molecules (26–101 nt) with complex topology containing pseudoknot or junctions (see Supplementary Table S1 online). The shorter RNA molecules without well-defined structures are not considered in the benchmark test. The predicted structures have a mean RMSD (Root Mean Square Deviation) value of 3.74 Å: 1.93 Å for duplexes, 3.6 Å for hairpins and 5.7 Å for complex structures. It should be pointed out that all the structural templates used in the tertiary structure predictions of a RNA molecule are from different molecules (see Supplementary Table S2 online). Furthermore, among the predictions for 300 RNAs, only 12 cases (PDB ID: 1AFX, 1ATV, 1D0U, 1J4Y, 1K6H, 1KKA, 1LU3, 1NEM, 1PJY, 1Q75, 1SZY and 1UUU) used 3D modules from the same structural family.

For hairpins and duplexes with/without internal loops and bulges, our methods can give high prediction accuracy. Fig. 1a and 1b are two examples of complex hairpin and duplex: the hairpin 28SP (28 nt) contains a large internal loop and the predicted structure has an interaction network fidelity (INF) of 0.89 and RMSD of 2.99 Å (Fig. 1a); the duplex 1I9X (26nt) contains two bulge loops and the predicted structure has an INF of 1.00 and RMSD of 2.73 Å (Fig. 1b). For hairpins and duplexes without internal and bulge loops the predictions have RMSD values less than 2 Å (see Supplementary Table S1 online).

Figure 1
figure 1

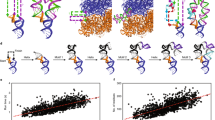
Predicted tertiary structures of typical RNA molecules.

(a) a hairpin with internal loop (28SP), (b) a duplex with two bulges (1I9X), (c) the pseudoknot 1KPZ, (d) Hammerhead ribozyme RNA 1NYI, (e) tRNA 1J1U and (f) SRP RNA 1Z43. The predicted structures (blue) are superimposed on their respective experimental structures (gold).

Full size image

The 3dRNA is not limited to predict RNA tertiary structures with simple topology and small size. It can also give reliable accuracy (5.7 Å on average) for RNA molecules with complex topology and larger size. For examples, the predicted structure of the pseudoknot 1KPZ (27 nt) has an INF of 0.73 and RMSD of 3.46 Å (Fig. 1c); Hammerhead ribozyme 1NYI (39 nt) is a Y-shaped structure with three-way junction and the predicted structure has 2.59 Å RMSD with 0.84 INF (Fig. 1d). It is worthy to note that the junction template used in the prediction is selected from different RNA family, signal recognition particle RNA (see Supplementary Table S2 online). The predicted structure of tRNA 1J1U (73 nt) is a standard L-shaped structure with four-way junction as the native one and has 3.80Å RMSD with 0.80 INF (Fig. 1e). In this prediction some 3D modules of the SSEs used to build tRNA are from other tRNA structures. If we remove all of them, the modeled tRNA 1J1U has a RMSD of 4.53 Å over all heavy atoms. Fig. 1f shows an example of large RNA, the signal recognition particle RNA 1Z43 with 101nt and the predicted structure also has a satisfactory accuracy (5.86 Å RMSD and 0.78 INF). These results show that all predicted structures have the same topology as the native ones.

We compare 3dRNA with five popular methods FARNA5, RNA2D3D3,8, MC-Sym7, iFoldRNA10 and V-fold model12. The RMSD values of our predictions are calculated over all heavy atoms and the predicted structures are not further refined by molecular dynamics.

Figure 2a shows the comparison of 3dRNA with FARNA and V-fold model. Since the programs of FARNA and V-fold are unavailable at present, the prediction results in the FARNA paper5 and V-fold model paper12 are used. In these cases all RMSD values are calculated over C4 atoms (see Supplementary Table S3 online). The mean RMSD value of our predictions is 1.19 Å and 0.66 Å smaller than FARNA and V-fold model, respectively. FARNA has updated to FARFAR recently6 and with the full use of the information of the secondary structure, tertiary motifs and RNA alphabet, the prediction accuracy of FARFAR is better than 2.0 Å RMSD for 14 out of the 32 benchmark tests. However, FARFAR is mainly applicable to short RNAs (6–20 nt). The prediction accuracy of 3dRNA using only secondary structure information is similar (2.3 Å heavy-atom RMSD on average) to FARFAR for short RNAs.

Figure 2
figure 2

Comparison of the prediction results of 3dRNA, iFoldRNA, RNA2D3D FARNA, V-fold model and MC-Sym.

(a) The C4-atom RMSD values of the predictions of 13 RNA molecules in the FARNA paper. (b) The RMSD distribution of the predictions of 185 RNA molecules. (c) The RMSD and (d) INF values of 32 RNA representatives with the sequence identity between any two of them being less than 50% from 185 RNA molecules. The RMSD values in (b) and (c) are calculated over all heavy atoms.

Full size image

We further compare 3dRNA with iFoldRNA, RNA2D3D and MC-sym (Fig. 2b to 2d). In this case, duplexes are not included because iFoldRNA, RNA2D3D and MC-sym are inapplicable. For fair comparison, we use the same sequence and secondary structure information and also the same method of calculating INF and RMSD values used in our manuscript. For MC-sym we used the online MC-sym server (option: model_limit = 1000 or time_limit = 12h) to predict the best models with lowest score. For RNA2D3D we used the RNA2D3D program to generate the models by sequences and secondary structures with default parameters. We did not do any minimization or modification. For iFoldRNA, the results are just considered as a reference because the available online web server only use sequence information as input with default parameters and so it is unfair to compare with other algorithms. Fig. 2b and Supplementary Table S4 show the prediction accuracies and their distributions of the four programs for 185 RNA structures, respectively. The mean prediction accuracies of 3dRNA, iFoldRNA, RNA2D3D and MC-sym are 3.97 Å, 6.87 Å, 6.37 Å and 5.87 Å, respectively. We also cluster the 185 RNA structures into 32 classes with the sequence identity between any two of them being less than 50%. One representative for each class is selected for comparison (see Supplementary Table S5 online), including simple hairpin (1ZIH) and typical L-shaped tRNA with four-way junction. Figure 2b and 2c show that most RMSD values of our predictions are less than 4 Å. If don't consider the 101nt-long RNA 1Z43, the mean RMSD value of our predictions are 2.95 Å, 2.55 Å and 1.6Å smaller than iFoldRNA, RNA2D3D and MC-sys, respectively (see Supplementary Table S5 online). The mean INF value (0.88) of 3dRNA taking into account all interactions (Watson-Crick, non-Watson-Crick and stacking) is similar to RNA2D3D (0.85) and MC-sym (0.86) and larger than iFoldRNA (0.71). This is because 3dRNA, RNA2D3D and MC-sym are based on the secondary structure but iFoldRNA only on sequence. If adding secondary structure information, iFoldRNA has similar INF value as RNA2D3D15. The mean INF values taking into account only non-Watson-Crick interactions are 0.45(3dRNA), 0.33(RNA2D3D), 0.35(MC-sym) and 0.08(iFoldRNA), respectively. iFoldRNA predicted tRNA structure with a RMSD value of about 21 Å if only using sequence as input and about 11.0 Å if considering the secondary structure information15. 3dRNA can give prediction accuracy (RMSD) of about 4.0 Å for tRNA using only secondary structure information. For the 101nt-long RNA 1Z43, 3dRNA has accuracy of 5.86 Å RMSD and other methods are larger than 32 Å (Fig. 2c and Supplementary Table S5). These results show that 3dRNA can build tertiary structures of large RNA molecules with reasonable accuracy. It is noted that MC-sys can give more accurate predictions if it samples larger conformational space but this will be very time-consuming and also needs an accurate scoring function to select the best structure.

We also evaluated 3dRNA by using the problems of the RNApuzzles16. RNApuzzles is a CASP-like contest for blind RNA three-dimensional structure prediction. The first RNApuzzles contains three problems. Problem 1 is to predict an RNA dimer using only sequence information, Problem 2 an RNA square by giving secondary structure and 3D coordinates of inner strands and Problem 3 a riboswitch domain using sequence information only. For Problems 1 and 3, we first predict their lowest free energy secondary structures (see the Method section for the details) and then build their tertiary structures by 3dRNA automatically. It is noted that in both cases the predicted secondary structures have some differences from the experimental ones in the internal loops and bulge loops. For problem 2, we first use 3dRNA to predict a quarter of the tertiary structure including a complete loop. Then, we do 0.1 ns molecular dynamics simulation for the predicted structure and select the structure with its inner chain conformation having the lowest RMSD values with relative to the given one. Finally, we assemble four quarters into the entire structure using the inner-strand structure as reference. The predicted results of the three problems by 3dRNA and other methods are presented in Supplementary Fig. S2 and Supplementary Table S6–S8. For the RNA dimer in Problem 1, 3dRNA gives the lowest RMSD value (3.30 Å) with relative to the experimental structure among all the methods. For the riboswitch in Problem 3, 3dRNA gives the second lowest RMSD value (11.11 Å) among all the methods. This higher RMSD value is mainly due to the small difference between the predicted and native secondary structures of the junctions. In these two cases, if we use the native secondary structures extracted from the experimental tertiary structures, the prediction accuracies of 3dRNA are much higher: 2.64 Å RMSD for Problem 1 and 6.67 Å RMSD for Problem 3 (see Supplementary Tables S6 and S8 online). It is noted that in both cases the 3D modules used are from non-homologous RNA families. For the RNA square in Problem 2, the prediction accuracy of 3dRNA is 2.83 Å RMSD and is higher than the mean value. Our results can be downloaded at the 3dRNA web server.

Discussion

Current algorithms of RNA tertiary structure prediction share a major difficulty of predicting loop conformations. We found that in different molecules the 3D conformations of the loops of a given type and length (e.g., 4 nt hairpin loop) are close to each other if they have the same sequence (Supplementary Fig. S1). Even their sequences are different the backbone conformations are still similar. For example, for non-redundant hairpin loops of a length from 4 to 13 nt, the relative heavy-atom RMSD values of backbone conformations distribute mainly between 2 and 4 Å and those of whole chain conformations between 3 and 5.5 Å (Fig. 3). This may explain why our prediction accuracy is about 3.97 Å on average. Therefore, we can generate appropriate loop backbones and consider the directions of bases as much as possible by sequence alignment.

Figure 3
figure 3

The ratio of the number of (a) backbone and (b) whole chain conformations versus relative heavy-atom RMSD values for non-redundant hairpin loops of different lengths.

Full size image

At present the total number of the solved RNA tertiary structures is less than 900 and is still limited in order to build a complete database of basic tertiary units, especially for longer loops, junctions and pseudoknot loops. For example, there is only one structure for 8-way junction or 9-way junction. This is one of the main reasons that restrict the prediction accuracy of 3dRNA for larger RNA molecules. This limitation can be improved as the number of the solved RNA tertiary structures increases. The prediction accuracy can be further improved by refinement of loop regions using scoring function or molecular dynamics in explicit water with metal ions. Our method can also sample the space of solutions by using different 3D units. In this case you need long time to sample the solution space and you also need a good scoring function to pick out the correct structure, which is still an unsolved problem. In the 3dRNA webserver, the number of sampling is limited to ten at present in order to finish a prediction not using very long time.

In summary, we introduced an automated and fast prediction method of RNA tertiary structure by assembling basic tertiary structural elements hierarchically. The only input of our method is secondary structure and one prediction can be finished in a few minutes. Our method not only predicts hairpin and duplex structures with high prediction accuracy comparable to the best algorithm available at present, but also can give satisfactory prediction accuracy for RNA molecules with complex topology and large size, e.g., structures with junctions and pseudoknots. 3dRNA provides an efficient and reliable method of building RNA tertiary structures for larger RNA molecules if their secondary structures are available from prediction or experiment.

Methods

Database of 3D conformations of SSEs

Since we build RNA tertiary structure by assembling the SSEs, we constructed a database of 3D conformations of the SSEs with non-redundant sequences, i.e., having one different nucleotide at least. The pairwise similarities of the sequences of 3D SSEs in the database are lower (Supplementary Fig. S3).

This database is divided into sub-databases: base pairs of standard A-form, junctions with different ways (e.g., 3-way junctions, 4-way junctions and so on) and loop of a given length and type including bulge loops, internal loops, hairpin loops and pseudoknot loops (e.g., 4-nucleotide hairpin loops, 2-nucleotide bulge loop and so on). The 3D conformations of loops were extracted from Structural Classification of RNA (SCOR) database17, junctions from RNAJunction database18 and pseudoknot loops from pseudoknot tertiary structures in RCSB PDB database. If a SSE has more than one conformation, we select the one with the largest occurrence probability.

When we extract 3D conformations of SSEs we include one more base pair at its 5′-end, which will be superimposed on the 3′-end base pair of the preceding SSE during assembling process. This can make the connecting region between loop and base pair have a proper conformation and avoid steric clashes.

Network representation of RNA secondary structure

We build RNA tertiary structure in two steps: firstly assembling SSEs into hairpins and duplexes and then the later into complete structure. Therefore, we need know the locations of the SSEs and also hairpins and duplexes along sequence and connectivity between them. This can be easily done by representing the input dot-bracket strip of RNA secondary structure by a graph with the SSEs (pairing bases, various loops and junctions) as nodes and the connections between them as edges. The node type (loop or pairing bases), its location and connectivity along backbone can be easily determined from consecutive dots or brackets in the dot-bracket strip. The non-backbone connectivity can be found as follows: Firstly, we search adjacent SSEs (nodes) from 5′ to 3′ end to determine if they form a hairpin or duplex. This also determines locations and connectivity of internal and bulge loops. Secondly, we search remaining SSEs (nodes) to check if they could form duplexes with nonadjacent nodes; Finally, the remaining SSEs are taken as junction component. Thus, we obtained a network of the SSEs, which are stored in a temporary file and will be used to assemble them into complete structure in two steps.

Building hairpin and duplex tertiary structures

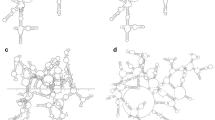
For hairpin or duplex RNA, we build their tertiary structure directly from the SSEs. The 3D conformation of each SSE is selected from our database with the highest sequence identity and at least one nucleotide matched to the target units (It is noted that the target and related molecules are removed in benchmark test)19. If there are several matches, we further compare the 3D elements with target elements nucleotide by nucleotide from 5′ to 3′ end and select the first element that matches the target element. Then, we assemble the selected 3D SSEs to tertiary structure from 5′ to 3′ end one by one. The adjacent elements are assembled together by superimposing the coordinates of C1′, C4′ and O5′ atoms of the 5′-end base pair of current SSE with those of the 3′-end base pairs of the preceding SSE. This is because these three atoms can represent the backbone architecture of the standard A-form conformation. Fig. 4a illustrates an example of this assembling procedure. Based on the sequence and secondary structure information of 1ZIH, we divide the structure into five SSEs (GCAA hairpin loop, G-U, G-C, G-C and C-G base pairs). The base pairs (G-U, G-C, G-C and C-G) are the standard A-form conformation. The GCAA hairpin loop is selected from ribosomal subunit structure 1J5E by sequence alignment algorithm. Then, the five SSEs are assembled one by one starting from 5′ to 3′ end. The first two SSEs are G-U and G-C base pairs. As mentioned above, the 3D modules of G-U and G-C base pairs have one more base pair at their 5′-end. We superimpose the coordinates of C1′, C4′ and O5′ atoms of this additional 5′-end base pair of 3D G-C module with those of the 3′-end base pair of 3D G-U module and then remove this 5′-end base pair. In the same way we add the third G-C pair and the fourth C-G pair to the assembled 3D module successively. Finally we assemble the additional 5′-end base pair of the 3D GCAA loop module with the 3′-end base pair of 3D G-U module and this completes the assembling process. Because the assembling does not preserve the chain connectivity very accurately, the assembled models are minimized (100 steps) with AMBER 98 force field20,21. The final predicted result is the structure after minimization.

Figure 4
figure 4

Schematic of assembling basic tertiary units.

(a) A simple hairpin RNA molecule containing one hairpin loop (GCAA) and four base pairs. (b) A complex three-way junction RNA molecule. See the main text for the detailed description.

Full size image

Building complex RNA structures

For complex RNA structures, we divide the whole RNA structure into independent hairpins and duplexes according to the network representation of the secondary structure22. We first construct the tertiary structures of these secondary components and then assemble them into the complete structure since hairpins and duplexes usually can be built with a high accuracy.

Fig. 4b illustrates an example of this assembling procedure. For large RNAs like signal recognition particle (SRP) RNA, we know from its graph representation that the whole RNA into four parts (two hairpins, one duplex and one three-way junction region). We first use the prediction strategy for hairpin and duplex above to build their tertiary structures, respectively. Then, we select the junction structure by comparing the length and sequence identity from our junction database. Finally, we assemble all the four parts into the complete tertiary structure from 5′ to 3′ end in a similar way as above. Again, the final predicted result is the structure after minimization.

Secondary and tertiary structure analysis

The S2S program is used to analyze and compare the base pairs of the native and the predicted tertiary structures23. RMSD (Root Mean Squared Deviation) and INF (Interaction Network Fidelity) against experimental structures are calculated to measure the prediction accuracy. The RMSD values are over all heavy atoms. The INF is used to evaluate the local interactions in contrast to the global architecture as RMSD values and its value is between 0 and 1. INF is calculated by using the positive predictive value (PPV) and sensitivity (STY) as follows24:

TP is the true positives interaction value, FP is the false positives interaction value and FN is the false negatives interaction value. The ptraj program in AMBER 11 is used for calculating the RMSD values. The tertiary structure visualization and figures are generated using VMD25 and PyMOL (http://www.pymol.org/)26.

In the calculations of the problems of the RNApuzzles16, we use the RNAshapes algorithm27 to predict the lowest free energy secondary structures of the RNA dimer and riboswitch domain. Since RNAshapes can work only for a single chain, a UUCG hairpin loop is added to connect the two chains of the RNA dimer but it is later removed from the predicted secondary structure. For problem 2, we do the 0.1ns molecular dynamics simulation for the predicted three-dimensional structure by using Amber program20,21 with AMBER 98 force field. All evaluation parameters are calculated using the same methods as the ref.16. For examples, the base pairs of native and predicted models are extracted by MC-Annotate28 and the clash scores are calculated by MolProbity29.

The 3dRNA web server

Our method of building three-dimensional RNA structures is provided at the 3dRNA web server (http://biophy.hust.edu.cn/3dRNA/3dRNA.html). The input of the 3dRNA server is (1) RNA sequence, e.g. GGGCGCAAGCCU and (2) RNA secondary structure in dot-brackets style, e.g. ((((….)))). You can load them from txt-format files or just paste them into the corresponding input windows. To accelerate the computation, you can also choose a structure type first: hairpin, duplex, pseudoknot or structure with junctions. Then, submit your job by clicking the “run” button. Once a task is submitted to the 3dRNA server, a web page is displayed to show the running steps and result. You can download the predicted RNA structure in pdb format from the result page or receive it by email. The datasets we used to test our program can also be downloaded from the 3dRNA web server.

At present the total number of the solved RNA tertiary structures is about 900 and is still limited in order to build a complete database of SSEs, especially for different longer loops and junctions. Therefore, to give reliable prediction, in our 3dRNA program the lengths of bulge loops are restricted from one to three nucleotides, the internal loops from one-one (internal loop with one nucleotide in one side and one nucleotide in the other side) to four-four, the hairpin loops from three to fourteen nucleotides and the terminal unpaired nucleotides is from zero to three. The junctions are limited to three-way and four-way. However, the 3dRNA can easily include long loops and junctions if we can collect enough data in the database of the 3D conformations of SSEs.