Introduction

Spintronics1,2, a new sub-disciplinary field of condensed matter physics, has been regarded as bringing hope for a new generation of electronic devices. The advantages of spintronic devices include reducing the power consumption and overcoming the velocity limit of electric charge1. The two degrees of freedom of the spin enable to transmit more information in quantum computation and quantum information. In the past decade, many interesting phenomena emerged, moving the study of spintronics forward. The spin-Hall effect predicts an efficient spin injection without the need of metallic ferromagnets3 and generates a substantial amount of dissipationless quantum spin current in a semiconductor4. All these provide the fundamental on designing spintronic devices, such as spin transistors that were predicted several years ago5. Experimental progresses have also been made in recent years6,7.

Since Rashba stated problems inherent in the theory of transport spin currents driven by external fields and gave his definition on the spin current tensor Jij8, there were several works on how to define the spin current in different cases. Sun et al. suggested that there was no need to modify the traditional definition on the spin current, but an additional term which describes the spin rotation should be included in the previously common-accepted definition9,10. A modified definition given by Shi et al.12 solved the conservation problem of the traditional spin current in the spin-orbit coupled system. His definition ensured an equilibrium thermodynamics theory built on spintronics, in accordance with other traditional transport theory, for instance, the Onsager relation. Jin, Li and Zhang11 first gave the continuity-like equation of the spin current in SU(2)×U(1) unified theory. The non-conservation of the spin current was due to the non-Abelian feature of the Yang-Mills field and an angular momentum was intentionally introduced to cancel the non-conservation effect. They made an analogical derivation on the non-relativistic Schroedinger Equation and did not use the Noether theorem. Thus, it is difficult to perform an exact analysis on the continuity of the spin current and the result can not be used in the systems in which the relativity should be considered (the electron behavior obeys the Dirac equation).

Spin-Hall effect, a vital phenomenon induced by spin-orbit coupling, has been extensively studied for years, although the microscopic origins of the effect are still being argued. Hirsch et al.13 referred that anisotropic scattering by impurities led to the spin-Hall effect, while an intrinsic cause of spin-Hall effect was proposed by Sinova et al.3. Both theoretical and experimental work reported recently demonstrated the achievements of spin polarization in semiconductors14,15,16.

In this study, the spin current Js, orbit angular momentum (OAM) current JL and the total angular momentum (TAM) current JJ, as well as the corresponding continuity equations have been delivered. In our tensor form expressions, the velocity operator α and the spin operator Σ can well display the physical meaning of the spin current. In addition, the non-relativistic approximation (NRA) expressions have been derived and the quantum effects have been predicted, which can not be deduced from previous definitions. Its vital effect on the finite size effect of the spin current is calculated in Hg/CdTe system. It is recommended to use the effective TAM and its current to replace the traditional spin and spin current in spintronics.

Results

The angular momentum current in a tensor form

According to the quantum electrodynamics(QED) theory17, the Lagrangian

can be represented in two terms

and the corresponding Hamiltonian of is well-known as

According of the Noether theorem, one can derive the following equation

while the corresponding Noether current is

where the spin current density Js is expressed as

and the OAM current JL

with . Here γµ is the Dirac Matrix and . The deduction details of Eq.(7) are shown in Methods.

The Lorentz invariance of the Lagrangian ensures the conservation of TAM current JJ of electrons. Eq.(6) shows that the spin current alone is not conserved, unless the orbital angular momentum is fixed.

The tensor form in three dimensional space

It is necessary to bridge the definition of the spin current JS with the traditional descriptions in spintronics. Using the operator and , the Eq.(7) turns as follows (see details in Methods)

thus the spin current operator is

where and are the velocity operator and the spin operator in Dirac equation, respectively.

In the traditional definition9, the spin current density operator means the carriers with a spin flowing at a speed of . However, the traditional definition based on an analogy of the classical current can not accurately describe the spin current, because the spin is an intrinsic physical character in quantum theory.

In relativistic quantum mechanics, the physical meanings of the velocity operator has been clearly described. Also, it should be pointed out that, there is a relationship between the electric current and the spin current in order (which is shown in the Discussion). The spin-orbit coupling effect demands to replace the momentum operator with the operator .

Deriving the expression of the OAM current JL and the TAM JJ is similar to that of spin current Js:

where OAM operator .

Angular momentum current of photons

Generating and manipulating the polarization of electrons is vital for spintronics. The main method is by letting the electron absorb or emit photons, in order to change its spin state.

The corresponding terms to describe the photon's spin current, the OAM current and the TAM current for the Maxwell field are

respectively. Here . Obviously, only the TAM current meet the continuity equation

By choosing the TAM current JJ (without the photon field) or (in the general occasion), one can keep the traditional theory unchanged, like the Onsager relation and the conservation law, which are built on the equilibrium state theory.

The NRA expression

In order to easily discuss and describe the physical meanings of the current expression, it is necessary to have a non-relativistic form of the spin current. After some tedious simplifications (shown in Methods), we derive the non-relativistic expression of the spin current, the OAM current and the TAM current.

where two important relations

are used. The result is shown to be completely equivalent to Eq.(9),(10) and (11) up to the order of . Obviously, not only the traditional term of the spin current, but also the other term

contributes to the spin current in the same order.

In quantum physics, there are some quantum effects that can not be analogized with the classical theory. The term (18) can only be described as “similar” as a kind of quantum rotation. In Sun's work9, the extra term ωs is used to describe the spin rotation, because a complete description of a vector current should include translation and rotation motions as the classical theory shows. Here, the term (18) which is accurately deduced yields two important conclusions as follows: Firstly, the traditional definition of spin current can not make the spin conserved, which has been widely accepted. Secondly, the term (18) causes the so-called quantum rotation, inducing the nonconservation property of the spin current, which is mentioned in Sun's paper9 and in Jin's paper11.

More importantly, because the term (18), with an “i” in its coefficient, stands for its quantum effect that can not be analogized classically, it does not only contribute to the magnitude of the spin current in the same order compared with the traditional definition, but also predict some important effects, such as the spin Hall effect.

Helical edge states in Quantum SHE system

We choose Kane model for semiconductors confining in a heterojunction of HgTe/CdTe. The parameters are adopted from the reference18.

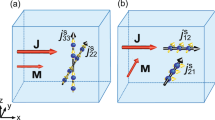
Fig. 1 shows the spin current of our definition. The wave functions Ψ(kx, y) are the edge states for L = 200 nm. It is shown that the current exists not only in the bulk, but also on both edges (dependent on the spatial distribution parameters of the wave functions λ1, λ2 and kinetic momentum k in reference18), while, no spin current exists according to the traditional definition

with .

Figure 1
figure 1

the spin current of Ψ↑+ (kx, y) at k = 0.01 nm−1,Ψ↓− (−kx, y) at k = −0.01 nm−1, the spin up, spin down,and the sum.

Full size image

When k = 0, the spin current still exists on the surface, as shown in Fig. 2. This distinctive character other than the traditional electric current has been discussed in previous papers1,3,4.

Figure 2
figure 2

the spin current of k = 0 nm−1: the spin up, spin down and the sum.

Full size image

It should be pointed out that the surface effect of the spin current can be much more enhanced due to the existence of the term (18). Because the quantum rotation is much stronger at the edges, it contributes much more than the traditional definition of the spin current.

The conservation and the continuity equations

As pointed out, the conservation of spin current is a contradictory issue. Different conclusions have been drawn for taking different occasions into consideration. In non-relativistic quantum mechanics, the spin is a conserved quantity when the OAM is frozen. The continuity equation is

When the OAM is not frozen (suitable for most spintronic systems), the continuity equation (19) turns into

The spin-orbit coupling effect makes the spin not a good quantum number any more. Because of the TAM J is a good quantum number, one can only choose the TAM and its corresponding current JJ to describe the transport phenomena. The QED theory points out that the electron's TAM can not stay in conservation in the external field. The Lorentz transformation of the system's Lagrangian gives out the continuity equation

Eq.(20) shows that the TAM of the system (the electrons and the photons) stays in conservation. It can be written in another form

The existence of enables the electrons and the photons to exchange angular momentum by some specific rules. This is exactly the theoretical support on the experiments, namely by absorbing and emitting the photons, the electron's TAM can be changed. Since the spin current itself is not conserved, its rate equation can be derived using the Heisenberg equation of motion (shown in Methods).

The TAM in semiconductors

The NRA of the Dirac equation Eq.(5) can be written

where

and

H2 is called the spin-orbit coupling, which is one of fundamentals of the spintronics. To study the transport properties, the electromagnetic susceptibility should be taken into calculation. In the case of the media having a relative velocity respect to the carriers, the electromagnetic field in the polarized media interacting with the carriers is

where is the relative speed of the media in the field. By placing these relations into Eq.(21) and utilizing the relation

the Hamiltonian (up to ) turns to be

The spin-orbit coupling H2 turns into a larger . According to the QED theory, the spin-orbit coupling is induced by the electric field in which the electron moves at a speed of acting on the electron's spin.

For the moving carriers, one should include the OAM into calculation, considering the electromagnetic polarization in the solid-state media under the external field. This means that not only the spin, but also the OAM is coupled with the electric field. When , the coupling term (28) turns back to be Eq.(29), the same as the traditional spin-orbit coupling. When , however, the orbit angular accumulation affects the coupling term to the same extent as the spin. Thus the OAM becomes crucial to describe the polarization of the system.

According to the theory of the spin-Hall effect, the carriers carrying different spins flow in the opposite directions. In our case, the carries with different angular momenta (j, jz) flow in the different directions. The only difference is that the OAM is included in our model. It should be noticed that the condition usually holds for most semiconductors, such as III-V compound semiconductors like GaAs and GaN. Thus,

According to the relation of the effective Lande g value and the effective mass, g in Eq.(30) should be replaced by g* in the semiconductors19. These imply that should replace the spin, as the physical quantity in more general cases.

Discussion

According to Eq.(15), the non-diagonal matrix element of the spin current that can be determined by

which is proportional to the matrix element of the current density operator in the QED.

Eq.(31) shows that the spin current of Jxz is proportional to the charge current Jy. This result coincides with the experimental data in Kato's work6, which strongly supports our definition. Therefore, the theoretical approach to estimate and calculate the spin current in terms of the density of electronic states has been provided. Meanwhile, the relation between the spin Hall conductance and the charge conductance has been formulated, laying the foundation of the electrically induced electron-spin polarization in spintronics.

Zhang proposed a semi-classical Boltzmann-like equation to describe the distribution of the spins20. The similar behaviour can also be deduced from our definition, considering the finite size effects. In the system, the spin up current is

The Jt and Je are the traditional definition of the spin current and the extra term (18), respectively. As shown in Methods, Jt is proportional to kx, namely

But Je is independent on kx and is only as a function of the density distribution of electrons in y direction, namely

This is a similar result compared to the Eqs. (12) and (13) in Zhang's work20. The spin accumulates in y direction, which is exactly the same as his conclusion drawn from the anomalous Hall field. The spin diffusion is decided by the parameters ω and D in his study. However, in our expression, the spin diffusion is determined by the spatial distribution parameters λ1 and λ218. Now Let us discuss the spin-Hall effect in GaAs bulk system with consideration of the spin-orbit coupling effect. According to Eq.(28), the Rashba effect can be written in cikiji. , and accumulate on one edge while , , on the other edge, namely the TAM j accumulates in both edges. It is easy to find that on both sides,

The Kerr angular rotation21 is proportional to whose expression is

where Ψa is the ground state, Ψb is the excitation state and is the energy gap. When , the Kerr rotation occurs.

The TAM j accumulation gives the same image as the traditional spin-Hall effect. Note that the spin does not accumulate actually, so the OAM plays an important role on the accumulation. Moreover, because the TAM J offers more degrees of freedom, one can use it to transmit more information under the same conditions. In summary, the spin-orbit coupling has been regarded as the TAM j coupling with the electric field in systems with a large . It is recommended that the TAM j current replaces the spin current to describe the motion of the carriers with different angular momenta. The physical nature of polarization accumulation and the Kerr rotation can be explained using our theory.

Methods

The definition of spin current

The Lagrangian of the system17 of is

According to the Noether theorem, when ,

When ,

Here, is the current operator of the spin s and is the current operator of the OAM.

where .

The tensor form

In Dirac representation, we have

The NRA form of spin current

The tensor form of the spin current is

and

where . Thus,

The Eq. (35) turns to be

The NRA expressions of the OAM current and the TAM current are similar, except for that the (σ)Σ should be replaced by the operators L and J, respectively.

The momentum current of Photons

The Lagrangian of the system of s = 117 is

Similar to , . According to the Noether theorem, one gets

The OAM current and the spin current are

where .

The motion equations of angular momentum currents

According to the Heisenberg equation, we have

Because of the relations

namely,

the Eq.(36) turns into

The spin-Hall effect in the finite size effect

For the edge states Ψ↑+

For the edge states Ψ↑−

The Spin-Orbit coupling in media

According to the Maxwell equations in the media

the first term in the NRA of Dirac equation turns to be

Therefore,