Introduction

Problems are the heart of mathematics. The set of 23 influential mathematical problems posed by David Hilbert inspired a great deal of progress in mathematics science (Hilbert, 1902). Einstein even advocated that raising new problems and new possibilities to regard old problems from a new angle requires creative imagination and marks a real advance in science (Einstein and Infeld, 1938). Therefore, problem-posing plays a critical role in mathematics.

In the 1980s, mathematical problem-posing (MPP) emerged in the area of mathematics education but was seldom considered an independent teaching and learning activity (Kilpatrick, 1987; Silver, 1994; Stoyanova, 1997). Later curriculum standards initially emphasized the importance of mathematical problems posing in teaching mathematics (see, e.g., NCTM, 1989, 1991; MOE, 2012, 2022). Meanwhile, many studies focus on the teaching of problem-posing (see, e.g., Kar, 2015; Lowrie, 2002; Dang et al. 2023b); developing the ability to pose problems (see, e.g., English, 1997; Crespo, 2003; Bicer et al. 2020); exploring the problem-posing strategies and processes (see, e.g., Kilpatrick, 1987; Silver, 1994; Stoyanova, 1997; Silver and Cai, 1996; Silver et al. 1996; Cai and Hwang, 2002; Lv and Wang, 2006; Cai et al. 2013; Cai et al. 2015; Van Harpen and Sriraman, 2013; Lee, 2021; Zhang et al. 2022; Cai et al. 2022; Cai, 2022). For instance, the “what-if-not” strategy (Brown and Walter, 2005); the five stages of problem-posing (Gonzales, 1998); the four thinking processes of problem-posing (Christou et al. 2005); the thinking strategy of problem-posing with six specific strategies (Cruz, 2006); the five activities (situation analysis, variation, generation, problem-solving, and evaluation) in the problem-posing processes (Baumanns and Rott, 2022), and the general problem-posing process model which contains four phases of orientation, connection, generation, and reflection (Cai and Rott, 2024); and various techniques (see, e.g., Kontorovich et al. 2012, Silver et al. 1996, Dang et al. 2023a), such as constraint manipulation, goal manipulation, targeting a particular solution, symmetry, generalization, and chaining, etc.

However, Kontorovich et al. claimed that the strategies in problem posing were not systematically classified and lacked empirical research about the types of problems posed in a specific task (Kontorovich et al. 2012). Students always pose related and parallel problems in the problem-posing tasks (Silver and Cai, 1996), and investigating the performance of students’ MPP from a progressive perspective is increasingly important (Liljedahl and Cai, 2021). Cai explored the mathematical thinking of Singaporean students in problem-posing and problem-solving and found that there were significant differences between fourth- and fifth-grade students (Cai, 2003). Guo et al. evaluated the performance of MPP of Chinese junior high school students (Guo et al. 2021). However, what mathematics problem-posing strategies students would prefer to use (Cai and Leikin, 2020) and how students pose mathematical problems in a given situation need further revealing (Cai et al. 2022). Meanwhile, it is necessary to investigate the performance of students’ mathematical problem-posing strategies from a progressive perspective. The open literature did not fully investigate which strategies students prefer to use and the processes undertaken in MPP (Cai and Leikin, 2020). Further, current research on MPP is highly lacking in such empirical studies, i.e., an investigation and analysis of a large scale of participants to explore the general pattern of junior high school students’ applications of mathematical problem-posing strategies during they engaging in MPP, and explore the variability and selectivity of junior high school students use of MPP strategies at different grade levels. Therefore, this is our motivation for conducting this survey, and we intend to construct an analytical framework to uncover phenomena about the specific strategies that Chinese students prefer to use when posing problems and the tendency between grades.

In this paper, we would like to examine the following two research questions:

  1. (1)

    Which strategies would junior high school students prefer to use in problem-posing tasks with specific situations?

  2. (2)

    How do the strategies develop for junior high school students as the grade level up?

Theoretical considerations

Definitions

Silver defined problem-posing as the generation of new problems based on a given situation or the reformulation of given problems (Silver, 1994). Students who pose mathematical problems reflect their thinking processes, and their performance depends on the strategies they use (Uittenhove and Lemaire, 2012).

Strategies of problem posing

Strategy is “a procedure or a set of procedures to achieve a higher-level goal or task” (Lemaire and Reder, 1999) and is not only specific to a particular situation but also cognitive processing programs that can be used in the face of a class of situations, with certain universality and generalization. Problem-posing strategies are the processes of cognitive processing and the methods used in the process of posing problems and are a systematic way of analyzing and transforming the conditions of a given problem-posing task and generating problems (Kontorovich et al. 2012). Problem-posing strategies refer to some specific techniques that problem-posers can adopt when they pose better mathematical problems. Problem-posing strategies can be used independently or jointly (Dang et al. 2023a). Problem posers always use different strategies (Lemaire et al. 2000; Siegler, 2007) and are always influenced by whether they are required to solve the given problem and will use different strategies to pose problems (Lavy and Bershadsky, 2003). Further, there are differences in the problem-posing strategies used by students at different grade levels (Xu, 2019). Strategies are not heuristics only, but also the approaches adopted by problem posers when they execute a task of problem posing. However, so far, problem posing has not resulted in a model comparable to the problem-solving model—Polya’s problem-solving techniques.

Many researchers built useful strategies or processes of MPP, such as Kilpatrick (1987); Silver et al. (1996); Contreras (2003, 2007); Christou et al. (2005); Gonzales (1998); Moore-Russo and Weiss (2011); Koichu and Kontorovich (2013); Crespo and Harper (2020); Baumann and Rott (2021, 2022); Dang et al. (2023a), Cai and Rott (2024). Following the “what-if-not” strategy (includes selecting a starting point, listing attributes, applying the ‘What-if-not?’ strategy, asking problems, and analyzing the problems) (Brown and Walter, 2005), Silver et al. surveyed 81 teachers who worked either individually or in pairs using the billiard task and found that the teachers posed problems using not only by generating goal statements while keeping problem constraints fixed but also by manipulating (Silver et al. 1996). In addition, they also found that the most prominent of the related problems posed by subjects were chaining and systematic variation in the clusters of posed problems. However, Silver et al. did not specifically examine MPP strategies, and the participants are not junior high school students. Koichu & Kontorovich conducted a case study on two students and obtained the following strategies for problem-posing: warming up, searching for an interesting mathematical phenomenon, hiding the problem-posing process in the problem formulation, and reviewing (Koichu and Kontorovich, 2013). Cruz developed a framework for the mathematical problem–posing strategy: object selection, classification of components, object transformation, an association of concepts, searching for dependencies, and posing of the question (Cruz, 2006). Weiss et al. proposed generative pathways for problem-posing on authentic mathematics, containing five tips: strengthening/weakening the hypothesis, strengthening/weakening the conclusion, generalizing, specializing, and considering the converse (Weiss et al. 2009). However, the research of Weiss et al. concentrates on analyzing a collection of narratives written by and about research mathematicians and applies to mathematical sciences research, not suitable for junior school students. One quite recent literature examines what strategies mathematicians often use when posing mathematical problems (or even mathematical conjectures), but it also does not involve the strategies that junior school students choose when posing mathematical problems (Dang et al. 2023a). There has also been little research addressing the selection of strategies for mathematical problems posing in large samples of participants.

Processes of problem-posing

The strategies and processes of MPP are used for analyzing the mechanisms of the problem posing in the problem-posing task (Baumanns and Rott, 2021). Many studies investigated the processes of mathematical problem posing. Cai and Cifarelli determined the cognitive process of college students’ mathematical problems posed in billiards tasks and then derived two strategies: data-driven reasoning and hypothesis-driven reasoning (Cai and Cifarelli, 2005). Christou et al. describe four thinking processes in problem-posing: editing, selecting, comprehending/organizing, and translating quantitative information (Christou et al. 2005). Baumanns and Rott introduced a descriptive phase model for problem-posing based on structured situations (situation analysis—the problem posers capture single or multiple conditions of the initial task; variation—changing or omitting single or multiple conditions; generation—constructing single or multiple new conditions; generation; problem-solving; and evaluation) (Baumanns and Rott, 2022). The model provides a better understanding of problem-posing processes and also provides additional insights compared to existing models (e.g., Cruz, 2006; Pelczer and Gamboa, 2009), distinguishes the variation and generation of the active types, encompasses non-content-related episodes, the model can also be used to characterize the different degrees of quality of the problem-posing process. Cai and Cai et al. developed a problem-posing-based learning instructional model containing four steps that are being used as teaching ways in mathematical classes for more than one problem-posing task or combination tasks of problem-solving and problem-posing. The model reflects the processes and strategies of problem posing from the perspective of applied problem posing (Cai, 2022; Cai et al. 2022). The three steps (analyze, select, and sequence) therein provide constructive advice on the research of processes and strategies for problem posing. Further, Cai and Rott constructed a general descriptive problem-posing process model which includes four phases of orientation, connection, generation, and reflection (Cai and Rott, 2024). In general, some of the problem-posing strategies and processes mentioned above stem directly from based on the situations and pose new problems based on given problems, and are consistent with the definition of Silver. However, these previous studies lack a complete framework of problem-posing strategies that start from the given situation and build on the problems that have been posed.

Differences in problem posing

Different mathematical problem posers will give different solutions or pose different problems when faced with the same problem-solving task or problem posing task. Research on problem-posing variabilities and differences is a new research direction in the study of variables of problem posing. Cai et al. (2022) gave brief instruction on variables in mathematical problem-posing tasks, such as the type of problem situation (real-life, mathematical), problem-posing prompts, educational level of the problem poser (primary school student, middle school student, high school student, college student, etc.), and size (e.g., individual, group, class). Cai explored the mathematical thinking of Singaporean students in problem-posing and problem-solving and found that there were significant differences between fourth- and fifth-grade students (Cai, 2003). Guo et al. investigated the performance of MPP in different situations of Chinese junior high school students and found that there were irregular changes in MPP as the grade level up and students had difficulty in posing extended mathematical problems (Guo et al. 2021). However, what mathematics problem-posing strategies students would prefer to choose (Cai and Leikin, 2020) and how students pose mathematical problems in a given situation need further study intensively (Cai et al. 2022).

Kontorovich et al. designed a framework for handling the complexity of MPP in small groups with five steps: task organization, knowledge base, problem-posing heuristics and schemes, group dynamics and interactions, and individual considerations of aptness (Kontorovich et al. 2012). Baumanns and Rott developed a three-dimension analysis framework to assess the problem-posing: generating and reformulating, routine and non-routine problems, and metacognitive behavior (Baumanns and Rott, 2021). The three dimensions are conceptualized to develop analytic tools for assessing problem-posing activities. To evaluate the problems posed by students, researchers always use the three indexes: the numbers, novelty, and profundity of the posed problems. Different from above, we will use statistics to analyze the performance and difference of problems posed by junior high school students.

The literature on the research of strategies and processes of problem posing is very abundant, but the literature on differences in problem posing is lacking. However, the processes of strategy selection and the developmental patterns of problem-posing are not clearly understood and need further investigation. In particular, how junior high school students choose various strategies in problem-posing tasks and how to analyze and assess their product of problem posing remain two critical aspects in the area of problem posing.

Theoretical framework

Mathematical thinking in problem-posing is divided into three stages: the input stage, the information-processing stage, and the output stage. In the input stage, problem posers need to understand the problem situation (Zhang et al. 2022). Lv and Wang showed that problems originate from the cognitive conflicts that arise for problem posers to understand the problem situation (Lv and Wang, 2006). After understanding the situation, the poser will attempt to pose problems. Processing the information in the initial situation in the problem-posing tasks is a kind of way for problem-posing, for instance, applying the strategies of “what-if-not”, constraint manipulation, goal manipulation, adding, modifying, and changing (Gonzales, 1996; Silver et al. 1996) and other operations (e.g., see Dang et al. 2023a). In the output stage, the posers write down their problems.

From the definition by Silver, the problem-posing strategy can be considered in two aspects: posing problems directly from the situation (category A) and posing further problems based on existing problems (category B).

In category A, pose mathematical problems by using the given situation. Therefore, this requires a good understanding of the situation (Crespo and Sinclair, 2008). For example, for the semi-structured mathematics situation of \({x}^{2}+{y}^{2}={z}^{2}\), Brown and Walter developed two types of strategies for generating problems from the situation (Brown and Walter, 2005). One needs to accept the given, e.g., by posing the problem “What is the geometric meaning of \({x}^{2}+{y}^{2}={z}^{2}\)?” The second needs to challenge the given, e.g., changing the equation to \({x}^{2}+{y}^{2}={1+z}^{2}\) or \({x}^{2}+{y}^{2}{ < z}^{2}\), and then problems can be posed based on the new expressions. The classification is based on whether the information in the situation has changed. Silver et al. subdivided the strategy of changing the information in the situation into changing the initial conditions and changing implicit assumptions (Silver et al. 1996). Thus, Silver et al. focused not only on whether the information was changed but also on what the changed information was. Furthermore, Gonzalez investigated the methods used by the posers and found that they used strategies such as adding data, changing values, changing conditions, and changing backgrounds when they directly posed problems in a given situation (Gonzales, 1996, 1998).

In category B, a new problem usually comes from other problems that are familiar to the posers. So, how do students pose a series of problems? Schoenfeld gave some suggestions on how to pose new problems by applying heuristics in different ways, such as considering special cases, changing the given numbers, or adding additional restrictions (Schoenfeld, 1985). Silver and Cai studied 509 high school students and confirmed that they could generate a series of related problems from the existing problems (Silver and Cai, 1996). Stoyanova analyzed the responses of eighth and ninth-grade students who posed problems based on a given computational problem and classified three strategies from the students’ problems posing: reformulation (reformulating a specific problem in their own words without changing the mathematical nature of the problem), reconstruction (vary and reorganize different levels of activities), imitation (problem-posing product is obtained from the given problem or situation) and invention (create new problems which do not know how to solve) (Stoyanova, 1997).

Common to the early studies was the attempt to change the scope of a problem, the known conditions, the relevant variables, and the structure of the problem. Silver et al. found that the most explicit relationships between the problems were chaining, systematic variation, and symmetry (Silver et al. 1996). These relationships reflect the specific ways of thinking of the posers when they pose new problems from existing ones.

According to the results of Silver et al. (1996) and Kontorovich et al. (2012), when the objectives and conditions of one problem are exchanged in another problem, the relationship between the two problems is called symmetry.

Systematic variation refers to a critical aspect of a problem that is held constant, while other critical aspects are varied systematically (Silver et al. 1996).

Chaining refers to the relationship in which later problems are generalizations of earlier problems or in which earlier problems provide direct conditions or help for thinking about and answering later problems (Silver et al. 1996), and the difference from systematic variation is that the problems are not parallel but recursive. In the billiard task of problem-posing, “What is the relation of the table dimensions to the final pocket?” and “What is the relation of the table dimensions to the number of hits?” are systematic variations. The essence of the problem remains unchanged, i.e., the relationship between the two variables is found, and a new mathematical problem is formed by changing the word “pocket” to “number of hits”; “Calculate the sum of consecutive odd numbers from 1 to 5,” “Calculate the sum of consecutive odd numbers from 1 to 100,” and “Calculate the sum of consecutive odd numbers from 1 to 2n+l” are a set of chain problems.

Now we wish to construct a novel analytical framework of students’ problem-posing strategies based on categories A and B, as shown in Fig. 1 and Table 1, which consists of posing problems directly from the situation and posing further problems based on existing problems. Category A includes A1 accepting the given information in the situation and A2 changing the given information in the situation, among which A2 is divided into A21 changing the initial information (adding additional information and changing the information) and A22 changing the implicit assumptions. Category B includes B1 symmetry, B2 systematic variation, and B3 chaining.

Fig. 1
figure 1

The framework of strategies of MPP.

Full size image
Table 1 Description of the framework of strategies of MPP.
Full size table

In our analytical framework, the participants are Chinese junior high school students who were not trained in mathematical problem posing before. Therefore, although several literatures describe many strategies for mathematical problem posing, such as Brown and Walter (2005), Silver et al. (1996), and Dang et al. (2023a), we have followed the definition of mathematical problem posing by Silver (Silver, 1994) and therefore select the strategies of category A (posing problems directly from the situation) and category B (posing further problems based on existing problems) to investigate the samples of junior high school students’ responses.

Methodology

An empirical study to reveal the selections and differences in mathematical problem-posing strategies of some Chinese junior high school students was conducted. The main research instrument is a paper-and-pencil test with three mathematical problem-posing situations, and the statistical methods used here are one-way ANOVA, multiple comparisons, and path analysis.

Sample

The sample for this study consisted of 1653 grades 7 to 9 from three junior high schools in Kunming, Lanzhou, and Beijing in China. The participants are with average academic levels in each grade. The sample statistics appear in Table 2.

Table 2 Sample statistics.
Full size table

Research design

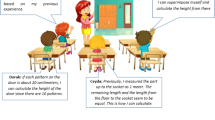
We aim to apply the same test questions to examine the strategies used by students when posing mathematical problems to reflect whether and what differences exist in students’ strategy choices and developmental characteristics. Three different problem-posing tasks are presented in Fig. 2, requiring students to pose as many different mathematical problems as possible according to the given situation within 30 min (Guo et al. 2021). All three tasks started from non-goal-specific situations, and students have opportunities to pose arbitrary mathematical problems and involve more exploratory and generative thinking (Silver, 1990; English, 1998), and the tasks are all open-ended, and the students at each grade level could pose mathematical problems. Three different problem-posing tasks shown in Fig. 2 are well-designed for junior high school students in each grade. As the participants go through the three problem-posing tasks, they will pose diverse problems whatever. Researchers do not require students to pose mathematical problems related to what they have learned about mathematics.

Fig. 2
figure 2

Three tasks of problem posing.

Full size image
Fig. 3
figure 3

The analysis and classification of a sample of problems.

Full size image
Fig. 4
figure 4

Two examples of students’ problem posing in the medical situation and real-life situation.

Full size image

Data encoding and reliability

Before coding the data, we first screened the students’ responses, and if there were two mathematical problems in one sentence, they were recorded as two different problems; if problems had the same meaning but were expressed differently, they were recorded as the same problem. Then, we coded the students’ responses in the following steps:

  1. (1)

    Identifying the classification of each Problem Cluster (PC). Summing up the variety of problems posed by students in three tasks in Fig. 2, one type is the problems posed directly from the given situations, that is, the initial problems in Fig. 1, and the other type is the related problems posed based on the initial problems, using symmetry, chaining, and systematic variation. Accordingly, we first divided the classification of problem clusters consisting of the initial problem and related problem. If using symmetry (or systematic variation; or chaining) to pose a related problem based on the initial problem, we noted Problem Cluster 1 for short PC 1 (or Problem Cluster 2 for short PC2; or Problem Cluster 3 for short PC3). When students did not use the symmetry, chaining, and systematic variation strategies, all problems posed were initial problems and belonged only to category A.

  2. (2)

    Determining the strategies used in each classification of PC. The strategies used by the students were determined according to Table 1. The initial problem-posing involved category A and the related problems posed involved category B. Figure 3 shows a student’s problem-posing responses in a real-life situation task; the performance in each PC and strategy/sub-strategy is also described.

  3. (3)

    Scoring of the strategies used. The score of the problem-posing strategy is based on the number of times the strategy is used. Specifically, no use of the strategy is scored as 0 points, and n times is scored as n points. Taking the scores of PC 1 in Fig. 3 as an example, the student’s strategy use was as follows: posing the initial question from the situation, using A211 in strategy A; posing the related problems based on the initial problem, using B1 in strategy B. Therefore, the student’s problem-posing strategy was scored as follows. Scoring for category A: Score(A1) = 0, Score(A2) = 1, then Score(A) = 1. Scoring for category B: Score(B1) = 1, Score(B2) = 0, Score(B3) = 0, then Score(B) = 1. The scoring for PC 2 or PC 3 is the same. It is important to note that the use of chaining may involve multiple related problems. Figure 4a and Table 3 below show another example of coding and scoring in a medical situation.

Table 3 Encoding and scoring of a sample of problems posed in the medical situation.
Full size table

We randomly sampled the responses of 165 students. These samples were then independently coded by two researchers, and the coding consistency was about 90 percent. Therefore, the coding consistency was available. The inconsistencies will be discussed and agreed upon by the two researchers. Formal coding will be carried out afterward.

Results

The main results concerning the two research questions are as follows.

What MPP strategies would junior high school students prefer to use?

The data in Fig. 5 provide a good illustration of the applicability and appropriateness of this framework. For example, students were able to pose problems by category A or category B, they could pose problems by accepting or changing the given information or assumptions in the situation, and the different problems they posed showed characteristics of symmetry, systematic variation, or chaining.

Fig. 5
figure 5

Data statistics of students’ strategies.

Full size image

The data revealed that concerning the selection of strategies for posing problems based on the situation, the students were most likely to accept the given information in the situation (A1), followed by changing the information in the situation (A2) to pose mathematical problems and adding information (A211) was the primary strategy for changing the initial information (A21) in the situation. Interestingly, the study found that a few students (13.49%) were able to pose new problems using the change implicit assumption strategy (A22). Regarding the selection of a strategy to present related problems based on initial problems, the students were more inclined to use chaining (B3) than symmetric (B1) and systematic variation (B2).

For category A in Fig. 5, of the 1,653 students, 94.68% used A1, while 84.27% used A2 (A21 or A22) to pose problems. Further sorting out the data found that 81.06% were able to use both A1 and A2 to pose problems. Among the A2 strategies used, the largest number of students (83.63%) posed problems by A21, and only a small number (13.49%) focused on A22. Moreover, in terms of the average number of times the strategy was used per student, not only did the majority of students choose the strategy of A1, but the average number of times the strategy was used per student was also the highest (M = 3.09). Among the strategies for A2 (M = 2.07), A211 was used the most (M = 1.47), while A212 was used only 0.43 times per student, and the least used strategy was A22 (M = 0.17). Therefore, the study further tested the significant difference between the use of A1 and A2 and found that there was a significant difference in the number of times students used A1 and A2 to pose mathematical problems (t = 15.775, p <0.001,2-tailed).

The data showed that more than three-quarters of the students (77.56%) were able to use Category B to pose further mathematical problems based on the problems posed by Category A. For category B in Fig. 5, 64.31% of students used B3, followed by B2, and finally, B1. For the number of times per student used, the most frequently used was B3 (M = 1.17), followed by B2 (M = 0.66), and finally B1 (M = 0.29). The significance difference test by multiple comparisons showed that there was a significant difference in the number of times used between B1 and B2 (t = −11.11, p < 0.001, 2-tailed, and a significant difference in the number of times used between B1 and B3 (t = −25.163, p < 0.001, 2-tailed), together with a significant difference in the number of times used between B2 and B3 (t = −11.591, p < 0.001, 2 -tailed). Therefore, when junior high school students choose to apply strategies B1, B2, and B3 for mathematical problem posing, there is a significant difference between the three.

Figure 4b shows the problems in Task 1, which was posed by a grade 8 student A (female, 13 years old).

P1: If one buys ￥300 costume, which is more economical, option A or option B?

P2: If one buys ￥500 costume, which option is more economical?

P3: At what price range is option A the most economical? At what price range is option B the most economical?

P4: Write down the functions for options A and B in turn and find the range of the independent variable x.

P5: Draw the graphs of the linear functions of options A and B.

In the student’s responses, we can see all the five posed problems belong to A1 accepting the given information. Also, her responses used the strategies of A21 changing the initial information, B3 chaining, and B2 systematic variation (changed ￥300 into ￥500 or unknown) in problems P1, P2, and P3. The posed problems P4 and P5 are a chain of problems that start and are generalized from the problems P1, P2, and P3, indicating that students can pose a series of different problems at different levels of difficulty. Problems P4 and P5 were posed because the participant had just learned about linear functions and therefore related their knowledge of mathematics to the mathematical problems posed. This phenomenon shows that students may use mathematical knowledge and concepts they have already learned when forming their mathematical problems. The mathematical contents in problems P4 and P5 are related to the linear functions, which can be interpreted as students using what they know about mathematics to form the content of new problems. However specific mathematical content is not associated with strategy use, choice, and tendency. This characteristic is also consistent with the three problem situations designed for this study: each junior high school student, regardless of grade level, was able to formulate problem posing based on the problem situation, either for linear functions or for whatever other content they what.

How do MPP strategies develop for junior high school students as grades up?

Differences in strategy selection

The analysis of the data in Table 4 revealed that there were significant grade-level differences in the choice of problem-posing strategies among students in the seventh, eighth, and ninth grades. Ninth-grade students tended to accept the given information from the situation and use chaining when posing related problems. In seventh-grade students, the mean number for used strategies of changing the implicit assumptions, symmetry, and systematic variation are the most among the three grades. Eighth-grade students tended to use the strategy of changing the given information (or changing the initial information) and the mean was bigger than seventh and ninth-grades. Reversely, for eighth-grade, the mean of strategies of changing the implicit assumptions and symmetry are the lowest among the three grades. Regardless of the grade level held, accepting the given information and chaining strategies were the most frequently used. Therefore, there was a more concentrated tendency in the selection of MPP strategies for students of different grades. The selection of MPP strategies is characterized by grades. The selection of strategies is diverse rather than linearly evolving.

  1. (1)

    Regarding the selection of problem-posing strategies at different grade levels, Table 4 presents the highest mean found for the total number of problems posed in ninth grade (M = 7.66, SD = 16.599), and the lowest mean and the highest dispersion was found for the total number of problems posed in eighth grade (M = 7.16, SD = 19.709), while the lowest dispersion was in seventh (M = 7.36, SD = 13.832).

  2. (2)

    Table 5 shows the result of the one-way ANOVA on the strategies used by the three grades. For category A, the one-way ANOVA indicated that there was no significant difference in the overall number of times students used strategies across the three grades (A: F (2,1650) = 1.773, p > 0.05). For A1 in category A, as the data presented in Table 4, the mean for the ninth grade (M = 3.25, SD = 3.512) was the biggest, followed by eighth grade (M = 3.08, SD = 5.628), seventh grade (M = 2.96, SD = 2.333) was the least. The one-way ANOVA found significant differences in the distribution of the number of times in the three grades (A1: F(2,1650) = 3.043, p < 0.05, η2 = 0.004, 90% CI[0,0.009]). On A1, the multiple comparisons (see Table 6) found significant differences between seventh and ninth grades, no statistically significant differences were found between seventh and eighth grades, eighth and ninth grades on the number of strategies they used.

Table 4 Statistics of the problem-posing for the three grades.
Full size table
Table 5 Results of the one-way ANOVA on the strategies used by the three grades.
Full size table

Similarly, the data illustrated there was a significant difference in the distribution of changing the initial information strategy (A21) between the three grades (A21: F (2,1650) = 9.730, p < 0.05, \({\eta }^{2}=0.012\),\(90 \% {\rm{CI}}\left[0.004,0.021\right]\)), with the differences mainly between seventh and eighth graders and eighth and ninth graders. For changing implicit assumptions strategy (A22), there were significant differences in the distribution of the number of times the students used changing the implicit assumptions in the three grades (A22: F (2,1650) = 31.121, p < 0.05, \({\eta }^{2}=0.037\), \(90 \% {\rm{CI}}\left[0.022,0.052\right]\)), with a significant difference in the number of times students used the strategy between the seventh and eighth grades and between the seventh and ninth grades (see Table 6).

Table 6 Multiple comparisons between grades for categories A and B.
Full size table

(2) For category B, in the distribution of the number of times used, there was a significant difference in the three grades (B: F (2,1650) = 15.913, p < 0.001, \({\eta }^{2}\) = 0.019, 90% CI [0.009, 0.031]), with the significant differences between seventh and eighth grades (p < 0.001) and eighth and ninth grades (p < 0.001), while the difference between seventh grade and ninth grade was not statistically significant. For B1, the mean for seventh grade (M = 0.37, SD = 0.355) was the biggest, followed by ninth grade (M = 0.26, SD = 0.292) and finally, eighth grade (M = 0.24, SD = 0.294), and there was a significant difference in the three grades (B1: F (2,1650) = 8.638, p < 0.001, \({\eta }^{2}\) = 0.010, 90% CI [0.003,0.019]), among which the significant differences between seventh and eighth grades (p <0.001) and seventh and ninth grades while between eighth grade and ninth grade was not statistically significant. For B2, there was a significant difference in the number of times used in the three grades (B2: F (2,1650) = 4.761, p < 0.05, \({\eta }^{2}\) = 0.006, 90% CI [001,0.013]), and significant differences between seventh grade and eighth grade and eighth grade and ninth grade, while there was no statistically significant distribution between seventh grade and ninth grade. For B3, a significant difference in the number of times in the three grades (B3: F (2,1650) = 14.948, p < 0.001, \({\eta }^{2}\) = 0.018, 90% CI [0.009, 0.031]), and significant differences between seventh grade and eighth grade, eighth grade and ninth grade, and seventh grade and ninth grade (see Table 6).

Dynamics of strategy selection

A confirmatory path analysis is conducted on the collected data using the structural equation models (SEM) through the software AMOS. Figure 6 shows the SEMs of the evolved strategies of problem posing of participating junior high school students and reflects the assumed framework of strategies of MPP we built in Fig. 1.

Fig. 6
figure 6

The SEMs of the evolved strategies of problem posing of junior high school students.

Full size image

Figure 6a depicts the SEM about the evolved strategies of problem posing on all the participants of grades 7, 8, and 9 which we investigated. As shown in Fig. 6a, we can derive the selection path of problem-posing strategies when students in junior high school experience one task of problem posing with the given situation in Fig. 2. After the students finish understanding the contents of the given situation, they always use A1 (accepting the given information) first to pose new mathematical problems, and then use strategy A2 (changing the given information) and then the path has ramified B3 (chaining) or B1 (symmetry) to pose new mathematical problems. One of the paths also shows that the problem-posing strategies used by students will transition directly from A1 (accepting the given information) to B3 (chaining). After using B1(symmetry), the students will always use B2 (systematic variation) to pose further mathematical problems. The path analysis shows that students generate new mathematical problems as they gain a full understanding of the given mathematical problem situations. At the same time, students are further confronted with new mathematical problems and then go on to pose new mathematical problems using various mathematical problem-posing strategies. This pathway is very much in line with our proposed problem-posing framework (Fig. 1).

Figure 6b–d depict the selections or evolutionary pathways of mathematical problem-posing strategies for junior high school students of grades 7, 8, and 9 respectively. There are differences in pathway selection and strategy evolution through the three grades. Figure 6a and b have almost the same pathways as the SEM. It shows that the pathways of the selection of problem posing strategies for grade 7 students followed well the path of selection of strategies for all students in the three grades.

Figure 6c and d show there are two separate pathways in the use of strategies for mathematical problems posed by students of grades 8 and 9: one is to pose problems by using A1 (accepting the given information), A2 (changing the given information), and B3 (chaining); another is to pose further problems by B1 (symmetry) and B2 (systematic variation) sequentially.

In conclusion, Fig. 6 demonstrates the dynamics of strategy selection and usage when students are engaging in the tasks of mathematical problem posing. From Fig. 6, we verified that our preconceived theoretical framework (Fig. 1) was largely consistent with the trends in strategy selection and use demonstrated by junior high school students during mathematical problem posing according to the given situations. The general trend in the selection of problem-posing strategies is from category A to category B. From A2 (changing the given information), the pathways will be facing the branches to B1 (symmetry) or B3 (systematic variation).

Path analysis of the selection of strategies for mathematical problem posing by grade 7 students revealed a diversity in the selectivity and dynamics of strategies used by them when posing mathematical problems, comparing the other grades. In Fig. 6b, for the students of grade 7, correlations are established between almost any two strategies when they are engaging in mathematical problem-posing tasks.

We have analyzed the findings using one-way ANOVA, multiple comparisons as well as path analysis. First, we should emphasize that the study is more comprehensive in its approaches to data analysis and is very much at the front line in the process of path analysis to investigate the pathways of evolution, selectivity, and diversity of mathematical problem-posing strategies among Chinese junior high school students at different grade level. Secondly, the pathway presented in Fig. 6 can be a good illustration of the fact that when junior high school students are engaging in the tasks of mathematical problem posing, they prioritize the use of accepting the given information to formulate new problems, followed by the use of strategies such as changing the given information to formulate new problems and symmetry/systematic variation/chaining for further problem posing. Therefore, we reveal the pattern of students’ choices in applying different mathematical problem-posing strategies under our analysis framework of the strategies of MPP.

Discussions and conclusions

There are abundant results on the framework or phase (process or stage) of MPP (e.g., Kontorovich et al. 2012; Baumanns and Rott, 2021; Leavy and Hourigan, 2022; Cai, 2022; Cai et al. 2022; Cai and Rott, 2024). Our investigation focuses on which strategies would junior high school students prefer to use in problem-posing tasks with specific situations and their differences in the performance of problem posing and applying the analytical framework to evaluate the responses of students’ MPP, and try to track pathways and trends in the development of student strategies. For instance, (1) The framework provides students an effective pathway to pose a series of mathematics from different perspectives starting from the given situation, which specifically explains the meaning of “variation” in the stage model of problem-posing activity proposed by Baumann and Rott, and extends the structured situation in their model to the general situation (Baumann and Rott, 2022). (2) Categories A and B, including sub-categories in the framework, help reveal the process of students’ MPP, and the specific MPP strategies also provide targeted guidance in teaching practice. (3) The existing problem-posing strategies in the open literature seem dispersed, while this study provides a more comprehensive framework for the analysis of problem-posing strategies and has been successfully used in the survey to analyze the differences in strategies of MPP. (4) The results of the pathway analysis show the effectiveness of our theoretical framework of strategies of MPP in reflecting students’ usage of strategies in mathematical problem-posing tasks, especially selectivity, diversity, and evolving character.

At the stage of problem-posing according to the given situation, 94.68% of students first chose to explore new mathematical problems in the situation of existing information, 84.27% of students posed new mathematical problems by “changing” and the “changing” strategy that students preferred to use was adding information, with 1.47 times per participant, which was much higher than changing data or conditions. This demonstrates that students often make connections with knowledge and experience outside the situation to pose new problems when they are unable to organize and pose well-structured mathematical problems given the available information, which is inextricably related to the point mentioned by Kilpatrick that one of the basic cognitive processes involved in posing problems is an association (Kilpatrick, 1987). Cai and Hwang investigated cognitive differences in problem-posing between sixth-grade students in China and the United States by classifying the problems posed by students into extended (beyond a given initial figure or quantity) and non-extended problems and found that Chinese students posed problems in a sequence from non-extended to extended problems (Cai and Hwang, 2002), which is consistent with the chaining strategy in this study. Figure 5 also shows this trend.

Cai compared grade level differences, which explored the mathematical thinking exhibited by Singaporean students in problem-posing (Cai, 2003), and another study had similar findings (Guo et al. 2021). In our study, we found significant differences in the use of problem-posing strategies among seventh, eighth, and ninth grades, mainly in that ninth graders were more likely to accept information from the situation to pose problems and were more likely to use chaining strategies. Changing initial conditional strategies was more popular among eighth graders, while seventh graders’ performance by changing assumptions and using symmetric strategies was the best. It is evident that there is a greater concentration of tendencies at each stage, and thus the use of problem-posing strategies is stage-specific. Through our survey data, we found that of the 1653 students who participated in the study,34 did not use any strategies (the number of students in grades 7, 8, and 9 is 8, 16 and 10 respectively), 35 did not use any category A strategies (the number of students in grades 7, 8, and 9 is 9, 16, and 10 respectively), and 371 did not use any category B strategies (the number of students in grades 7, 8, and 9 is 93, 159, and 119 respectively). This shows that students have more difficulty in using strategies of category B than in using strategies of category A. Further, the mean number of strategies students of the ninth grade used (M = 7.58) is a bit bigger than the seventh grade (M = 7.26) and eighth grade (M = 7.05).

We focused on the developmental differences and selections in students’ MPP strategies. In the opening literature, some studies focus on students’ MPP performance from the perspective of learning progression. Si investigated the learning development process of problem-posing competency to examine how high school students’ MPP competency develops gradually over time with appropriate instruction (Si, 2014). Guo et al. emphasize that studying students’ ability to pose mathematical problems from a learning progression perspective is a very new topic (Guo et al. 2021). Therefore, comparing studies at different grade levels is of great value to research.

On the aspect of how the impact of prompts on MPP, Possamai, and Allevato investigated how situations and problem-posing prompts affect teaching through problem posing (Possamai and Allevato, 2024); Cai et al. examined the impact of different prompts on students’ problem posing (Cai et al. 2023). A limitation of this study is that it does not consider the effect of prompts on student responses. Therefore, how prompt influence the strategies selection by junior high school students, and the differences therein, require further research.

In conclusion, the findings from this study contribute to the understanding of problem-posing processes and problem posing strategies. Based on the constructed framework, we conducted an empirical study to reveal the differences and selections in students’ usage of strategies for MPP and the characteristics of grade development. The study also provides a systematic analysis of MPP strategies and to offer the actual data for large-scale sample students’ strategies status. It is hoped that the study could serve as a stepping stone in the quest to systematically and deeply understand MPP strategies. Moreover, the Chinese mathematics curriculum standards require a stage and developmental goal for MPP (Guo et al. 2021). Therefore, the theoretical framework of strategies of MPP and the findings here are also a scientific response to the curriculum standards.

Limitations and further work

Our sample was selected from China only, hence, subsequent studies may consider collecting samples from other countries. This study only reflects the selection and use of students’ problem-posing strategies based on their responses and then lacks the use of students’ voiced thinking to reflect their problem-posing process, and the selection of strategies. In addition, the framework of mathematical problem posing strategies in this study is only given based on Silver’s definition of mathematical problem posing, which is the shortcomings of this study and will be further improved in the follow-up.