Introduction

20-inch Large area photomultiplier tubes (PMTs) with photon counting capability1,2,3,4,5,6 are widely used in large scale neutrino and cosmic ray experiments. There are generally two types of large area PMTs: existing Dynode-PMTs and newly developed PMTs based on microchannel plate (MCP-PMTs)6 which was developed for Jiangmen Underground Neutrino Observatory (JUNO)7. JUNO proposed in 2012 is a multipurpose neutrino experiment designed to determine neutrino mass hierarchy and precisely measure oscillation parameters by detecting reactor neutrinos from the Yangjiang and Taishan Nuclear Power Plants, observe supernova neutrinos, study the atmospheric, solar neutrinos and geo-neutrinos, and perform exotic searches. The energy resolution was required to be \(3\%\sqrt{E(\mathrm{MeV})}\), which means that the detection efficiency (DE) of the large area photomultiplier tube (PMT) should be above 25%. At that time, DE of R3600, Hamamatsu 20-in. PMT applied in Daya Bay experiment, was just 15.4%. None of the 20-in. Dynode chain PMT product could meet this criterion. In this situation, a 20-in. large area MCP-PMT was proposed and developed by the MCP-PMT collaboration formed by the scientists from Institute of High Energy Physics (IHEP) of the Chinese Academy of Sciences, Northern Night Vision Technology Co., LTD (NNVT) and Xi’an Institute of Optics and Precision Mechanics (XIOPM) of the Chinese Academy of Sciences.

Compared with the typical dynode PMT (R12860 from Hamamatsu)8, the MCP-PMT (P6201 from NNVT)9 performs well in the rise time, collection efficiency (CE), peak to valley ratio and applied voltage for typical Gain, but in the transit time and transit time spread (TTS), it shows poor performances.

According to the shortcoming of the 20-in. large area MCP-PMT, a good time performance large area MCP-PMT design accompanied with high CE is proposed in this work. Simulations are conducted to systematically investigate CE and time performance for various operating and geometry parameters including the size and bias voltage of the two focusing electrodes and MCP. Based on the simulation results, a set of operating and geometry parameters are chosen.

Concept design and simulation

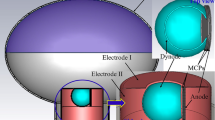
To obtain a good time performance, a new large area MCP-PMT with Ф 460 mm photocathode diameter is proposed in this paper. The schematic diagram is exhibited in Fig. 1 (right side). Compared to the existing MCP-PMT (left side), the structure of the new design has been greatly changed. Generally, in the PMT cavity, the curved equipotential surface shows better focusing characteristic, and the planar equipotential surface benefits the consistency of the transit time. To obtain both high CE and short TTS, the focusing system of the new design includes a cylindrical barrel (Electrode I, designed for short TTS) and a conical barrel (Electrode II, designed for high CE). A pair of MCPs are placed at the top opening of the conical barrel. Implementing millions of MCP channels in the three-dimensional model is impossible. Hence, a simplified model based on two MCPs without channels is adopted in our simulation. The glass envelope handle cooperates with the Electrode I, Electrode II and MCPs to generate the accelerating and focusing electric field which benefits CE and time performances.

Figure 1
figure 1

Schematic diagrams of the existing (left side) and new (right side) large area MCP-PMTs.

Full size image

Simulations are conducted to validate the feasibility. The new MCP-PMT model is simulated in CST Studio Suite10. The electric field, electron trajectories, energies and velocities are calculated based on the Finite Integral Technique and Monte Carlo method. The feasibility and effectiveness of this simulation approach has already been validated11,12,13.

Photoelectron trajectories from the photocathode to MCP are well simulated. 2000 photoelectrons uniformly distributed from 28.5° (corresponding to the photocathode edge) to 90°on photocathode are sampled by Monte Carlo method. The initial energy of electrons exiting the photocathode obeys β(1,4) distribution with mean value 0.15 eV in the range 0.0–0.6 eV. The emitted azimuth is uniform distributed over the range of 0–2π. Initial elevation follows Lambert cosine distribution from 0° to 90°. Owing to the short distance and high potential difference between the first MCP-in and anode, the electron transit time through the MCP is around several hundred picoseconds and TTS is just tens of picoseconds which thus are negligible. In our simulation, the transit time distribution between the photocathode and the first MCP is evaluated.

CE is defined as a ratio of the number of photoelectrons from the photocathode collected by MCP channels to the total number. Large area MCP-PMT employs coated MCP which is coated with high secondary electron yield (SEY) material on the flat inter-channel area and electrode penetrating in channels area, to obtain high CE11,14. A great deal of secondaries can be excited in the high SEY area and finally be collected by the MCP channels, which makes the acceptance fraction of the impinging photoelectrons close to 100%11. In our simulation, it is impossible to obtain the exact CE value attributing to the simplified MCP model approximated to a flat surface without channels. Thus, only the ratio of photoelectrons landing on the simplified MCP input flat surface (active area, CEa) is evaluated.

The dependence of CEa and time performance on the bias voltage and size of the two focusing electrodes and MCP is systematically investigated. Photocathode voltage is 0 V. Only one parameter is varied at a time, while the others are kept constant, with values listed in Table 1.

Table 1 Fixed parameters of the new MCP-PMT.
Full size table

Simulation results and discussions

Electrode I

The dependence of CEa and time performance on the applied voltage (UI), diameter (DI) and height (HI) of the electrode I is investigated. UI, HI and DI are varied from 0 to 800 V, 20 mm to 170 mm and 240 mm to 400 mm, respectively. For each computing, only one parameter is varied at a time, while the others are kept constant, with values listed in Table 1. Sample results with values of mean ± SD are graphically represented in Figs. 2, 4 and 5.

Figure 2
figure 2

CEa and TTS versus UI over the range of 0 V ≤ UI ≤ 800 V.

Full size image

In Fig. 2, decreasing CEa and TTS are observed as results of increasing UI. Figure 3 shows the electric field distributions in the PMT cavity for UI = 0 V (a) and 800 V (b). For UI = 0 V the electric field shows better focusing characteristic. It is helpful to obtain a high CEa. For UI = 800 V, the electric field between the photocathode and the top opening of electrode I is more uniform, which benefits the consistency of transit time which means short TTS. The CEa at UI = 0 V and 50 V is 100%. The shortest mean TTS is 0.93 ns at UI = 800 V.

Figure 3
figure 3

Electric field distributions in the PMT cavity for UI = 0 V (a) and 800 V (b).

Full size image

It is obvious in Fig. 4 that CEa gradually increases to a maximum of 100% at DI = 360 mm and then reduces to some extent with increasing DI. Besides, a decreased TTS by increasing DI is observed. The shortest mean TTS is 1.79 ns at DI = 400 mm. For smaller DI, the electric field shows better focusing property. Larger DI is benefit for the uniformity of electric field, and finally TTS.

Figure 4
figure 4

CEa and TTS versus DI over the range of 240 mm ≤ DI ≤ 400 mm.

Full size image

Figure 5 exhibits the simulated CEa and TTS, which result from the variation of HI over the range of 0–170 mm. CEa and TTS basically decrease with the increasing HI. From the visual electric distribution in the PMT cavity, it is observed that the electric field for lower HI shows better focusing property. Higher HI is benefit for the electric field uniformity. CEa is 100% for 0 mm ≤ HI ≤ 110 mm. The shortest mean TTS is 1.44 ns at HI = 170 mm.

Figure 5
figure 5

CEa and TTS versus HI over the range of 0 mm ≤ HI ≤ 170 mm.

Full size image

Electrode II

The applied voltage (UII), bottom diameter (DII-b) and height (HII) of the electrode II have significant impacts on CEa and time performance. UII, HII and DII-b are varied from 0 to 3500 V, 120–380 mm and 30–210 mm, respectively. For each computing, only one parameter is varied at a time, while the others are kept constant, with values listed in Table 1. Sample results with values of mean ± SD are graphically represented in Figs. 6, 7 and 8.

Figure 6
figure 6

CEa and TTS versus UII over the range of 0 V ≤ UII ≤ 3500 V.

Full size image
Figure 7
figure 7

CEa and TTS versus DII-b over the range of 120 mm ≤ DII-b ≤ 380 mm.

Full size image
Figure 8
figure 8

CEa versus HII over the range of 30 mm ≤ HII ≤ 210 mm.

Full size image

As can be seen in Fig. 6 that with the increasing UII, CEa increases to 100% at UII = 3300 V, and the mean TTS decreases until its minimum 1.73 ns at UII = 1900 V and then increases. With the increasement of UII, the electric field is divergent first, then approximately uniform (benefit for short TTS), finally focused (conducive to high CEa).

It is shown in Fig. 7 that increasing DII-b has positive effects on CEa and TTS. Electric field for smaller DII-b shows better focusing property. Larger DII-b is benefit for the field uniformity. DII-b = 380 mm is the optimum value, for which the mean CE = 96.8% and mean TTS = 1.7 ns.

Increasing HII has a slight negative effect on CEa (exhibited in Fig. 8) but no significant effect on TTS. The mean TTS changes from 1.74 to 1.85 ns over the range of 30 mm ≤ HII ≤ 210 mm. At HII (fixed value) = 150 mm, mean TTS is 1.79 ns. The highest mean CEa is 99.2% at HII = 30 mm.

MCP

Dependence of CEa and TTS on the input face of the top MCP applied voltage (UMCP) is well simulated. The total voltage applied on the two MCPs is 1000 V. Only UMCP is varied, while the others are kept constant, with values listed in Table 1. As is shown in Fig. 9 that with the increase of UMCP, CEa and TTS increase. Electric field for higher UMCP shows better focusing property but poorer uniformity. The highest mean CEa is 99.6% at UMCP = 3500 V. The shortest mean TTS is 1.54 ns at UMCP = 500 V.

Figure 9
figure 9

CEa versus UMCP over the range of 500 V ≤ UMCP ≤ 3500 V.

Full size image

Optimized model

Considering both high CEa and good time performance requirements, UI = 100 V, DI = 400 mm, HI = 130 mm, UII = 2000 V, DII-b = 380 mm, HII = 30 mm and UMCP = 2500 V are employed in the MCP-PMT model. Other parameter values are listed in Table 1. Simulation results show that the new design has a high CE and outstanding time performance.

Electron trajectories from the photocathode to the MCP input face is shown in Fig. 10. On the right side, the photoelectron trajectories from four points on the latitudes 30°, 45°, 60° and 90° with the mentioned initial angle spread are exhibited, and on the left side, photoelectron trajectories for such positions with initial angles of 30°, 45° and 60° (corresponding to the X–Z coordinates) are shown.

Figure 10
figure 10

Electron trajectories from the photocathode to the MCP input face.

Full size image

A sample transit time distribution result of 2000 photoelectrons from the whole photocathode is exhibited in Fig. 11a. The transit time and TTS are 40.5 and 1.48 ns, which are greatly improved than 120 and 15 ns of the existing MCP-PMT9 and 95 and 2.4 ns of the dynode PMT8. Transit time distributions of photoelectrons from latitudes 30°, 45°, 60° and 90° are shown in Fig. 11(b). Affected by the electric field in the PMT cavity, latitude 45° corresponds to the largest TTS which is 1.09 ns. Besides, results shows that the mean TTS is also 1.48 ns.

Figure 11
figure 11

Photoelectron transit time distributions. (a). Photoelectrons emitted from the whole photocathode. (b). Photoelectrons emitted from the latitudes 30°, 45°, 60° and 90° of the photocathode, respectively. FWHM is TTS.

Full size image

Photoelectrons incident positions on the MCP input face are well evaluated. Results are shown in Fig. 12. Photoelectrons from different latitudes land at different diameters on the MCP input face. With the increasing latitude, this effect become more obvious. For 30° and 45° Latitudes, the incident positions are indistinguishable. Simulation results show that the mean CEa of the photoelectrons from the whole photocathode is 97.5%, which mean that CE of the coated MCP-PMT is expected to be 100%.

Figure 12
figure 12

Incident photoelectron distribution on the MCP input face. 90° Latitude corresponding to the top point. Considering the symmetry of the MCP-PMT, photoelectrons are emitted from half of the photocathode. (a). Incident photoelectron position distribution on the MCP input face. (b). Incident radius distribution on the MCP input face.

Full size image

Conclusion

This work presents a new large area MCP-PMT design with good time performance. A novel focusing system with a cylindrical barrel electrode and a conical barrel electrode are designed. Three-dimensional models are developed in CST Studio Suite to validate the feasibility and effectiveness. Dependences of CE and time performance on the size and bias voltage of the focusing electrodes and MCP configuration are systematically investigated. Based on the simulation results, a set of operating and geometry parameters are chosen for the new MCP-PMT design considering both high CE and good time performance. Results show that the mean ratio of photoelectrons landing on the channelless MCP input flat surface is 97.5%. The mean TTS value of photoelectrons from the whole photocathode achieves 1.48 ns. It will be a good candidate for the detection experiments with high CE and high time resolution requirements.