Introduction

Higher-order topological insulators with robust unconventional states at their boundaries have been one of the most active research directions in condensed matter systems1,2,3,4,5,6,7,8,9 and have been rapidly extended to the classical systems10,11,12,13,14,15,16,17,18,19,20,21,22. An nth-order topological insulator in \(d\) dimensions protects topological states at its (\(d-n\))-dimensional boundaries, such as corners of two-dimensional (2D) systems and hinges of three-dimensional (3D) systems, in addition to the (\(d-1\))-dimensional topological boundary states. The reported works show that the hierarchical topological boundary states of higher-order topological insulators can be excited independently and selectively since the states are usually decoupled in both real and momentum spaces and belong to different energy ranges. The higher-order topological boundary states (e.g., corner and hinge states) have been used to design peculiar devices, such as topological lasing23,24 and interferometer25,26.

Adiabatic quantum pump, proposed in the dynamically periodic systems in one dimension by Thouless firstly, is a quantized transport process linked to the Chern numbers27. Subsequently, such topological pumps have been investigated in various systems28,29,30,31,32,33,34,35,36,37,38, such as ultracold atom29,30,31, photonic32,33, and acoustic systems34. Based on the topological pumps of bulk states, a variety of nontrivial physical effects have been observed, such as spin pumping35, nonlinear Thouless pumping36, and non-Abelian Thouless pumping37,38. In addition to the quantized topological bulk pumps, a generalization of adiabatic pump physics to the topological insulators gives the topological pumps of edge states, which have been realized in diverse platforms39,40,41,42,43,44,45,46.

Most recently, a higher-order topological pump, which is a combination of adiabatic pump physics and higher-order topology, has opened a new direction for topological phases28,47,48,49,50,51,52,53. Essentially, the higher-order topological pump is a dynamical realization of the higher-order topology1,2. Based on higher-order topological pumps, various interesting higher-order topological transport phenomena, e.g., corner-bulk-corner transport, which cannot be implemented in the conventional higher-order topological insulators, have been observed47,48,51,52,53. Note that the reported higher-order topological pumps are protected by bulk topologies, such as the bulk Chern number47,48.

In this work, we propose a periodically evolved tight-binding model (TBM) to implement the higher-order topological pump of corner states protected by the boundary Chern number, which is related to the adiabatic evolution of the bulk quadrupole moment. The higher-order topological pump indicates that corner states, crossing the edge band gap, can be used to adiabatically transport energy from one corner of the structure to its opposite corner through the edge states. We implement this model in phononic crystals modulated in their parameter dimensions and use it to demonstrate in an experiment that sound is transported as TBM predicted. The robustness of topological corner-edge-corner sound transport is identified. Furthermore, we have shown that the evolution path can be arbitrarily designed. As such, we can realize some interesting topological sound transports, e.g., topological splitting effects of sound, which are conclusively identified by our acoustic experiments.

Results

Tight-binding models

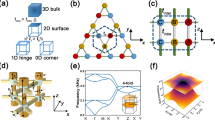
We first present a TBM for a 2D insulator whose properties are modulated in parameter dimension, as shown in Fig. 1a. Each unit cell includes four spinless orbitals (labeled as 1-4) with intra-cell couplings \({t}_{x}\left({\theta }_{z}\right)=0.5-0.3\cos {\theta }_{z}\), \({t}_{y}=0.2\), inter-cell couplings \({w}_{x}\left({\theta }_{z}\right)=0.5+0.3\cos {\theta }_{z}\), \({w}_{y}=0.8\), and on-site energies \({V}_{a}\left({\theta }_{z}\right)=-{V}_{b}\left({\theta }_{z}\right)=-0.1\sin {\theta }_{z}\). Note that the parameter \({\theta }_{z}\), ranging from \(0\) to \(2\pi\), is a closed one-dimensional parameter space. The Hamiltonian of TBM can be described by

$$H\left({k}_{x},\,{k}_{y},\,{\theta }_{z}\right)= \, {w}_{x}\sin {k}_{x}{\Gamma }_{4}+\left({{t}_{x}+w}_{x}\cos {k}_{x}\right){\Gamma }_{3}+{w}_{y}\sin {k}_{y}{\Gamma }_{2} \\ +\left({{t}_{y}+w}_{y}\cos {k}_{y}\right){\Gamma }_{1}-{V}_{a}{\Gamma }_{0},$$
(1)

where \({\Gamma }_{0}\), \({\Gamma }_{1,2,3}\), and \({\Gamma }_{4}\) are the direct product of two Pauli matrices \(\hat{\tau }\) and \(\hat{\sigma }\), i.e., \({\Gamma }_{0}={\tau }_{0}{\sigma }_{z}\), \({\Gamma }_{1,2,3}={\tau }_{x,y,z}{\sigma }_{x}\), and \({\Gamma }_{4}={\tau }_{0}{\sigma }_{y}\). Obviously, at \({\theta }_{z}=0\), the 2D system exhibits a topological insulator with bulk quadrupole moment \({q}_{{xy}}=0.5\). Modulated by \({\theta }_{z}\), the bulk quadrupole moment has the quantized value of \(0.5\) (\(0\)) at \({\theta }_{z}=0,\,2\pi\) (\({\theta }_{z}=\pi\)) and loses its quantization away from those \({\theta }_{z}\) values, see the data shown in Supplementary Fig. 1. Naturally, as \({\theta }_{z}\) goes from \(0\) to \(2\pi\), the 2D system changes from the quadrupole topological insulator to topological trivial insulator and back to quadrupole topological insulator, which is accompanied by no bulk band gap closure (see Supplementary Fig. 1). It is worth pointing out that the parameter \({\theta }_{z}\) together with the wave vectors \({k}_{x}\) and \({k}_{y}\) form a synthetic 3D parameter space, indicating that the model can be viewed as a synthetic 3D system. We have checked that this model carries zero bulk Chern number in the synthetic 3D parameter space (see Supplementary Note 1).

Fig. 1: Tight-binding models (TBMs).
figure 1

a, b Sketch of the TBM for phases I and II, respectively. c Top: \({\theta }_{z}\) evolution of the projected dispersion for a supercell of phase I that is periodic in the \(y\) direction but has \(15\) unit cells in the \(x\) direction, simulated at \({k}_{y}={{{{{\rm{\pi }}}}}}\). Bottom: The same as top panel, but for a supercell of phase I that is periodic in the \(x\) direction but has \(15\) unit cells in the \(y\) direction, simulated at \({k}_{x}={{{{{\rm{\pi }}}}}}\). d \({\theta }_{z}\) evolution of the projected dispersion for a 2D finite system of phase I that has \(15\) unit cells in both \(x\) and \(y\) directions, where gapless corner states (red and magenta dots, black and green stars) appear in the common band gap of the bulk and edge states. In c and d, the cyan (blue) dots are the twofold degenerate dots, indicating the left and right (top and bottom) edge states, and the olive dots represent the bulk states. e Typical eigenfields of the corner states in d. f, g are the same as c and d, respectively, but for phase II. h 2D finite system constructed by placing phases I and II together. i The same as d, but for the structure shown in h. j 2D structure constructed by cutting the structure shown in h along the red dashed line. k The same as i, but for the structure in j.

Full size image

Then we consider the \({\theta }_{z}\) evolution of edge properties of 2D system. The strips in the consideration contain finite complete unit cells, where their \({\theta }_{z}\)-dependent projected dispersions simulated at \({k}_{y}={{{{{\rm{\pi }}}}}}\) and \({k}_{x}={{{{{\rm{\pi }}}}}}\) are shown in Fig. 1c. It can be observed that the edges of both \(x\) and \(y\) directions present gapped states in \({\theta }_{z}\) space, see Supplementary Fig. 1 for more data. Note that the evolutions of \(y\) directional edge states in \({\theta }_{z}\) space exhibit nontrivial Chern number \({C}_{{{{{{\rm{E}}}}}}}=-1\) (see Supplementary Note 1), referred to as boundary Chern numbers. Essentially, the non-zero boundary Chern number originates from the quantized edge dipole pumping due to the adiabatic evolution of the bulk quadrupole moment, see Supplementary Fig. 2 for more details. The above analysis demonstrates that our system is a higher-order topological insulator with a boundary Chern number in the synthetic 3D parameter space.

When the system is applied with the open boundaries in both \(x\) and \(y\) directions, the nonzero boundary Chern number guarantees the existence of gapless topological states (i.e., corner states). This is further confirmed by the \({\theta }_{z}\)-dependent projected dispersions of the finite 2D system, as shown in Fig. 1d. Clearly, the gapless corner states traverse the gap between the bands of the bottom and top edges. Considering a process in which \({\theta }_{z}\) continuously varies from \(0\) to \(2{{{{{\rm{\pi }}}}}}\) in a very slow evolution speed, a topological pump between corner states will be achieved. To be specific, as \({\theta }_{z}\) increases from \(0\) to \(2{{{{{\rm{\pi }}}}}}\), the corner state is transported from the right bottom (left top) corner to the left bottom (right top) corner and back to itself through the bottom (top) edge state. This higher-order topological pump indicates that corner states can be used to adiabatically transport energy from one corner of the structure to its opposite one. However, such topological pump is unfavorable for experimental observations, since it requires a long evolution path (i.e., varying \({\theta }_{z}\) from \(0\) to \(2{{{{{\rm{\pi }}}}}}\)) and then makes energy transmission not fast enough to overcome the dissipation before it is pumped from one corner to the other.

To achieve a topological corner pump in a short evolution path, we also consider a topological phase, which can be constructed by interchanging the sites of the couplings \({t}_{x}\) and \({w}_{x}\), and changing the on-site energies of four sites. The new unit cell is shown in Fig. 1b. Hereafter, we denote the topological phases in Fig. 1a, b as phases I and II, respectively. For the same \({\theta }_{z}\) evolution, the bulk quadrupole moment of phase II has the quantized value of \(0\) (\(0.5\)) at \({\theta }_{z}=0,\,2{{{{{\rm{\pi }}}}}}\) (\({\theta }_{z}={{{{{\rm{\pi }}}}}}\)) and loses its quantization away from those \({\theta }_{z}\) values (Supplementary Fig. 3). Similar to the phase I, the evolution of the bulk quadrupole moment of phase II also gives rise to a quantized edge dipole pumping captured by a nonzero Chern number \({C}_{{{{{{\rm{E}}}}}}}=-1\), see Supplementary Note 2. All of those lead to different band evolutions for phase II, as shown in Fig. 1f, g. Compared to the data shown in Fig. 1c, d, the gapped edge states of x direction and gapless corner states appear in the range of \({0.5{{{{{\rm{\pi }}}}}} < \theta }_{z} < 1.5{{{{{\rm{\pi }}}}}}\), while the gapped edge states of y direction appear in whole range of \({\theta }_{z}\). By placing these two phases together (Fig. 1h), a new type of the higher-order topological pump is achieved, where the couplings \({t}_{1}\) (red) and \({t}_{2}\) (magenta) at the boundary between the phases I and II are designed as \({t}_{1}={-t}_{2}={w}_{x}\). As shown in Fig. 1i, as \({\theta }_{z}\) progresses, the corner states are pumped from the right bottom (top) corner of phase I to the left bottom (top) corner of phase II and back to itself through the bottom (top) edge states. If we cut the finite 2D system along the red dashed line (Fig. 1h), higher-order topological pump between the top corner states of phases I and II vanishes, as demonstrated by the dispersion shown in Fig. 1k. A similar phenomenon can be observed for the bottom corner states by cutting the finite 2D system along the blue dashed line in Fig. 1h. With the dispersion shown in Fig. 1k, we can realize a higher-order topological corner transport in short evolution path, such as varying the parameter \({\theta }_{z}\) from \(0.25{{{{{\rm{\pi }}}}}}\) \({{{{{\rm{to}}}}}}\) \(0.75{{{{{\rm{\pi }}}}}}\), paving a way for high-efficiency energy transmission. Note that the evolution functions of the parameters and the couplings \({t}_{1}\) and \({t}_{2}\) of the system are not unique, and such higher-order topological pump occurs as long as the evolution path does not close the band gap, see Supplementary Note 3 and Supplementary Fig. 4 for more details.

Acoustic realizations

The above evolutions of the TBMs can be directly implemented in an acoustic system consisting of a cavity-tube structure. As sketched in Fig. 2a, each acoustic unit cell of phase I consists of four air-filled cavities (gray and olive) coupled with narrow tubes (colored). The acoustic system has a square lattice and its lattice constant is \(a=10{{{{{\rm{cm}}}}}}\). The \({\theta }_{z}\)-dependent physics discussed above is realized by the structure parameters \({l}_{x}\left({\theta }_{z}\right)={n}_{0}-{\delta }_{0}\cos {\theta }_{z}\), \({s}_{x}\left({\theta }_{z}\right)={n}_{0}+{\delta }_{0}\cos {\theta }_{z}\), \({w}_{a}\left({\theta }_{z}\right)={n}_{1}+{\delta }_{1}\sin {\theta }_{z}\), and \({w}_{b}\left({\theta }_{z}\right)={n}_{1}-{\delta }_{1}\sin {\theta }_{z}\), where \({n}_{0}=0.5\,{{{{{\rm{cm}}}}}}\), \({n}_{1}=0.4\,{{{{{\rm{cm}}}}}}\), \({\delta }_{0}=0.3\,{{{{{\rm{cm}}}}}}\), and \({\delta }_{1}=0.04\,{{{{{\rm{cm}}}}}}\), and other parameters can be found in Supplementary Note 4, Supplementary Figs. 5 and 6. Similarly, the unit cell of phase II can be constructed by interchanging the \({l}_{x}\) and \({s}_{x}\), and changing the sizes of four cavities. We have checked that the bulk and boundary properties of phases I and II are in good agreement with the TBM predictions, where topological gapless corner states appear in the band gaps of the corresponding systems, see Supplementary Fig. 5. To implement the topological corner pump shown in Fig. 1k, we consider a supercell formed by assembling acoustic phases I and II together with the same boundary truncations as those shown in Fig. 1j. The calculated \({\theta }_{z}\)-dependent band structure is shown in Fig. 2b (Methods). As expected, a topological pump between the bottom corner states of acoustic phases I and II appears. Note that the spectral spacings between the pumping (red and magenta dots connected by the green dots) and edge state (green dots) bands exhibit closures at \({\theta }_{z}=0.5{{{{{\rm{\pi }}}}}}\) and \(1.5{{{{{\rm{\pi }}}}}}\), which is unfavorable for accessing the adiabatic condition in the experiments54,55,56. This dilemma can be released by scaling the size of the finite 2D system, where the finite spectral spacings at \({\theta }_{z}=0.5{{{{{\rm{\pi }}}}}}\) and \(1.5{{{{{\rm{\pi }}}}}}\) increase with decreasing size and a large spectral spacing allows for a faster pumping process55,56, see Supplementary Note 5 for more details. In this context, we choose the 2D system with size of \(3.5a* 3.5a\) for the acoustic simulations and experimental observations below.

Fig. 2: Acoustic realizations.
figure 2

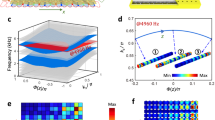
a Acoustic unit cell of phase I. b \({\theta }_{z}\) evolution of the projected dispersion for a supercell that has finite size of \(14.5a* 14.5a\) in \(x\)-\(y\) plane, where gapless corner states (red and magenta dots) appear in the common band gap of the bulk (olive dots) and edge states (green dots). The edge truncations of the 2D acoustic supercell are the same as those used in TBM (Fig. 1j). c The same as b, but for the acoustic supercell with interlayer couplers (purple in f), where supercell has the size of \(3.5a* 3.5a\) in \(x\)-\(y\) plane. During the calculation, the periodic Bloch boundary condition is applied in the \(z\) direction. The topological pump of corner states is represented by blue surfaces, whereas the bulk bands are labeled by olive surfaces. d The pumping curve of states at \(f=4.16\,{{{{{\rm{kHz}}}}}}\), corresponding to the intersection illustrated by the blue horizontal sheet in c. e Pressure field distributions of the topological states from right bottom corner to left bottom corner localization with the change of the pumping parameter \({\theta }_{z}\) from \(0.25{{{{{\rm{\pi }}}}}}\) to \(0.75{{{{{\rm{\pi }}}}}}\) along the \(z\) direction. f Numerical demonstration of topological corner-edge-corner transport at \(f=4.16\,{{{{{\rm{kHz}}}}}}\). Inset shows the details of the cavity with interlayer couplers (purple). g The same as f, but for the defect system. Inset presents the details of the defects. The cyan dots and black arrows in f, g represent the point sources and the propagations of sound, respectively.

Full size image

We now consider the higher-order sound transports based on the topological pumps between acoustic corner states. The topological pumps of corner states can be realized by stacking the \({\theta }_{z}\)-dependent 2D acoustic systems along its vertical dimension, i.e., the \(z\) direction, with interlayer couplings47. Here, the interlayer couplings in the \(z\) direction are realized by the uniform vertical tubes (purple in Fig. 2f), where the coupling strength can be tuned by the location and size of the tubes. Following the ref. 47, with such stacking procedure, the pumping curves of corner states are given by the spectrum of the collective states of stacked 3D crystal shown in Fig. 2c (Methods), which is a function of the pumping parameter \({\theta }_{z}\) and \({k}_{z}\). The spectrum reveals the existence of the gapped edge states (green surfaces) inside the band gap of bulk states (olive surfaces) and the existence of the gapless corner states (red and magenta surfaces) within the gap of edge states. Figure 2d shows the pumping curve of states at \(f=4.16\,{{{{{\rm{kHz}}}}}}\), which is chosen for the intersection of the dispersion surface of corner states with the plane at frequency \(f=4.16\,{{{{{\rm{kHz}}}}}}\) (Fig. 2c). The spatial profile evolutions of the states along the pumping curve are shown in Fig. 2e, which confirm that sound is indeed pumped from one corner to the other. Concretely, as parameter \({\theta }_{z}\) increases from \(0.25{{{{{\rm{\pi }}}}}}\) to \(0.75{{{{{\rm{\pi }}}}}}\), the state localized at the right bottom corner becomes the edge state and is further transformed into a state localized at the left bottom corner.

To elucidate the topological pump-based corner-edge-corner sound transport, a 3D sample constructed by stacking the 2D systems with discrete \({\theta }_{z}\) values is needed. Naturally, a sample with more 2D layers (i.e., variation \({\Delta \theta }_{z}\) from one layer to another is in small values) will be closer to the adiabatic topological pump47,48. Here, we consider a \(13\)-layer sample (Fig. 2f) within the adiabatic regime (Supplementary Fig. 7) to demonstrate the topological corner transport. The 2D systems of the sample are in the range from \(0.25{{{{{\rm{\pi }}}}}}\) to \(0.75{{{{{\rm{\pi }}}}}}\) and the variation of \({\theta }_{z}\) is \({\Delta \theta }_{z}=0.042{{{{{\rm{\pi }}}}}}\), see Supplementary Fig. 6 for more details. As shown in Fig. 2f, the sound wave, excited by the sound source located at the site marked by a cyan dot, does evolve from the right bottom corner to the left bottom corner as one walks along the stacking direction. It is of interest to evaluate the extent of the topological robustness of the higher-order sound transports in such conditions. To evaluate that, four hard cylinders with length of \(l=2\,{{{{{\rm{cm}}}}}}\) and diameter of \(d=0.35\,{{{{{\rm{cm}}}}}}\) are inserted into the four cavities of the bottom edge of the seventh layer of the sample (inset of Fig. 2g) and the topological corner-edge-corner pump in the defected structure is simulated, as shown in Fig. 2g. Comparing performance with the system without defects (Fig. 2f), the corner states can be smoothly pumped in spite of the presence of defects. This confirms that the pump we designed is robust against the reflections from defects. We have checked that a similar fast pumping effect can be observed in a non-adiabatic sample, see Supplementary Fig. 8.

Experimental observations

Figure 3a presents the experimental sample which has the same structure in Fig. 2f. In the experiment, the acoustic wave is excited by a point sound source of \(f=4.16\,{{{{{\rm{kHz}}}}}}\) at the position marked by a cyan dot, and the pressure distributions are measured by the microphone, layer by layer along the stacking direction (Methods). Figure 3d presents the experimental data, which captures well the simulation results shown in Fig. 2f. It shows that the sound signal indeed emerges from the right bottom corner and turns to the left bottom corner through the edge of 2D layers, along which the pressure field is strongly localized. Now we turn to confirm the topological robustness of such sound transport against defects. The experimental sample has a geometry employed in Fig. 2g. As shown more clearly in Fig. 3c, the defect is constructed by inserting four hard cylinders into the four cavities of the bottom edge of the seventh layer of the sample. The topological corner-edge-corner transport in the defected structure is experimentally measured. As shown in Fig. 3e, the experimental data agree well with the simulation results (Fig. 2g). Compared with the performance in the system without defects (Fig. 3d), the corner states can be smoothly pumped despite the presence of defects. This confirms the weak influence of the defects on the topological pump of acoustic corner states.

Fig. 3: Experimental observations of topological corner-edge-corner transports.
figure 3

a An image of the experimental sample. Circular holes are perforated in cavities for inserting the sound probe or point sound source, which are sealed with plugs when not in use. b Zoom-in photograph for the area marked by the red box in a. c The same as b, but for the sample with defects (green dots). Insets give the details of the normal plug (orange box) and plug (green box) with the hard cylinder. The hard cylinder (as a defect) has the same size as that in Fig. 2g, where \(l=2\,{{{{{\rm{cm}}}}}}\) and \(d=0.35\,{{{{{\rm{cm}}}}}}\). d Measured pressure fields (\(f=4.16\,{{{{{\rm{kHz}}}}}}\)) of the sample. Note that the sound signal attenuates as its propagation due to the inevitable absorption. For the clarity of demonstration, the data of each layer are normalized by the corresponding maximum value. e The same as d, but for the sample with defects. The 2D presentations of the data of d and e can be found in Supplementary Fig. 9. The cyan circles and black arrows in d and e represent the point sources and the propagations of sound, respectively.

Full size image

Based on the basic topological corner-edge-corner transport demonstrated above, we can realize some intriguing sound transports, such as topological splitting effects and topological abnormal reflections of sound. Here, the sample in Fig. 3a is referred to as \(\theta\) block. To implement the sound splitting effects, we construct a \(25\)-layer sample by mirror stacking two \(\theta\) blocks in the \(z\) direction, as shown in Fig. 4a, b. To map out pressure distributions of the sound split, we place a point source at the site marked by the green dot. As shown in Fig. 4d, the measured data exhibit that the sound signal splits into two directions and eventually reaches two-end corners, showing a perfect symmetric splitting effect and agreeing well with the simulated results in Fig. 4c (see also Supplementary Movie 1 for the beam splitting effect). However, if we put the point source at the site marked by a cyan dot (Fig. 4b), a topological abnormal reflection of sound is observed, as demonstrated by the numerical data shown in Supplementary Fig. 10 and Supplementary Movie 2. Similar beam splitting and abnormal reflection effects can also be observed in a \(9\)-layer non-adiabatic sample, as shown in Supplementary Fig. 8 and Supplementary Movies 3 and 4. Moreover, by modulating the evolution trajectory, other interesting topological sound transports can be observed, such as asymmetric topological sound splitting effect and chiral sound transmission (see Supplementary Note 6). Thus, our design, based on the higher-order topological pumps, provides a unique avenue for the manipulation of acoustic waves.

Fig. 4: Topological acoustic beam splitter.
figure 4

a Configuration of the \(25\)-layer sample. b An image of the \(25\)-layer experimental sample. c Simulated topological splitting effect of sound at \(f=4.16\,{{{{{\rm{kHz}}}}}}\). d The same as c, but for measured results. Again, the measured data of each layer are normalized by the corresponding maximum value. The 2D presentations of the data can be found in Supplementary Fig. 9. In b–d the cyan dot and green dots/circle label the point sources, and the black arrows represent the propagations of sound.

Full size image

Conclusions

In summary, we have experimentally demonstrated higher-order topological sound transports in modulated acoustic crystals through topological corner-edge-corner pumps. The topological corner pump is protected by the nonzero boundary Chern number, which originates from the quantized edge dipole pumping induced by the adiabatic evolution of the bulk quadrupole moment. Hence, the higher-order topological corner pump is fundamentally different from those reported previously, which are typically protected by bulk Chern numbers or bulk dipole moment47,48,49,50,51,52,53. Based on the higher-order topological pump, we have demonstrated that sound waves can be guided along an arbitrarily designed evolution path in 3D space, forming interesting transport phenomena, such as topological splitting effects. Physically, by dimensionally extending the proposed system from two spatial and one parameter dimensions to three spatial dimensions, our system is a synthetic 3D higher-order topological insulator with a boundary Chern number. The corner states during the topological pump now map to the chiral hinge states. Such chiral hinge states have not yet been directly observed in any artificial systems, although the theoretical realizations of chiral hinge states were proposed2,3,57,58. Thus, our results are dimensionally equivalent to the observation of chiral hinge states in a synthetic 3D higher-order topological insulator. Our findings pave the way for the study of higher-order topological physics and have potential applications in flexible energy transport and wave manipulation.

Methods

Simulations

All numerical simulations are performed by COMSOL Multiphysics, a commercial finite-element solver package. The resin used for sample fabrication is modeled as acoustically rigid for the airborne sound. The simulated band structure in Fig. 2b is calculated by a \({\theta }_{z}\) 2D finite acoustic supercell of size \(14.5a* 14.5a\). The acoustic supercell used to calculate the dispersion in Fig. 2c has the size of \(3.5a* 3.5a\) in \(x\)-\(y\) plane and interlayer couplers (purple in Fig. 2f and Supplementary Fig. 6), where the periodic Bloch boundary condition is applied in the \(z\) direction. The pumping curve in Fig. 2d is obtained by intersecting the dispersion surface of corner modes with the blue plane at frequency \(f=4.16\,{{{{{\rm{kHz}}}}}}\) in Fig. 2c. The pressure field distributions in Figs. 2f, g, and 4c are simulated for finite-sized samples.

Experiments

Experimental samples are fabricated by 3D printing with a fabrication error of ~\(0.1\,{{{{{\rm{mm}}}}}}\). The circular holes are perforated on cavities for inserting the point sound sources or sound probes. In the experiment, all the samples are surrounded by absorbers to eliminate boundary reflections. To obtain the measured pressure field distributions in Figs. 3d, e and 4d, sound waves are launched from a point source and detected hole-by-hole through a microphone of diameter ~\(1.0\,{{{{{\rm{mm}}}}}}\) (B&K Type 4182). The amplitudes of the pressure fields are recorded and frequency-resolved by a multi-analyzer system (B&K Type 3560B).