Introduction

Diabetes is one of the early diseases linked to an excessive chance of COVID-19 infection in society. According to the WHO, \(18.3\%\) of all deaths among people aged COVID-19 in Africa are attributable to diabetes. In recent years, based on WHO examination of data from 13 countries, the prevalence of diseases or coexisting conditions among those who tested positive for COVID-19 from Africa was compared to that of diabetes worldwide. The death rate was 10.2% per 1,000 people, or 2.5% per person1. One or more of the underlying mechanisms for the link between diabetes and COVID-19, including long-lasting redness, elevated coagulation enterprise, impaired unsusceptible reaction, and possibly direct injury by SARS-CoV-2, are studied2. We also discovered that individuals with comorbidities such as hypertension, interstitial lung disease, cardiovascular disease, and diabetes had greater odds of mortality, which was consistent with other investigations of COVID-19 in various populations3. Diabetes was more prevalent (32%) in instances that led to ICU hospitalizations than it was in non-hospitalized patients (6%) or non-ICU admission cases (24%)4. Similarly, early studies from Wuhan, China, revealed that patients with diabetes were overrepresented among COVID-19 fatalities. Also, the English data, which examined records of more than 17 million persons connected to 10,926 COVID-19-related fatalities, was the first research demonstrating an independent influence of diabetes status on COVID-19-related mortality5. This finding underscores the importance of monitoring and managing diabetes as a comorbidity in COVID-19 patients. It is observed from all the above reports that the risk of dying from COVID-19 infection is increased by some underlying diseases, especially diabetes6. Several mathematical models have been proposed to examine the transmission dynamics of COVID-19 in individuals with diabetes as an underlying condition7,8. Many scientific and engineering domains, including biological systems, make use of stochastic modeling. In these domains, adding stochastic noise to internal links facilitates auditory connections and a state of balance9.

Mathematical models are investigated with fractional order models for continuous monitoring instead of integer order nowadays. These fractional order models are based on fractional calculus, which deals with the integral and derivation for complex or real orders. An example of a fractional model is the extension of the dynamics of breast cancer cells to a system of fractal fractional partial differential equations, which was done to describe the dynamics of lethal breast cancer resulting from the combination of two medicines10. Some different fractional operator like caputo, CF, and ABC studied in11,12,13 and some applications of fractional also studied in14,15. For COVID-19 epidemic modeling, the SEIAQRDT model was transformed to fractional order, which improved its advantages16. The Laplace transform for the CF derivative was used to ascertain the global stability of the COVID-free equilibrium. Sensitivity analysis showed that in order to control epidemics, parameters with negative partial derivatives had to be maximized. In a nonlinear neutral stochastic fractional differential system, researchers17 investigated the existence and stability of solutions, demonstrating their existence and uniqueness through the use of fixed point theorems and the Banach contraction principle. The research18 used the CF derivative to model hearing loss in children caused by mumps, while the Euler approach used the CF derivative for approximation and fixed point theory for unique solutions. Nonlocal fractional differential equations of the Sobolev type with impulsive circumstances are studied in the work19. It takes a series of approximate integral equations and derives an associated integral equation.

More complex mathematical operators of differentiation are required for more complicated physical problems. Fractal function analysis combines the ideas of fractional calculus with the complexities of fractal geometry, and is studied by mathematicians who specialize in fractional calculus. In this domain, the power rule, the exponential decay rule, and the generalized Mittag-Leffler rule are considered to be the three basic laws. Power rule, exponential purpose, or Mittag-Leffler purpose are examples of local derivatives that are necessary in Caputo-type situations; earlier work20 introduced fractal–fractional operators, which combine fractal and fractional calculus. When describing real-world data and modeling mathematical concepts, fractal–fractional operators work better21,22,23,24,25,26,27. Using power law kernels and fractal–fractional operators, a new model was created28 for a particular type of influenza virus. Leray-Schauder theorem and special mappings were used to analyze solutions. The numerical solutions were approximated using the Adams-Bashforth technique. In29, the presence of unique solutions for the fractional-fractal operator for diabetes mellitus model is investigated. First, the constitutive equations were used to formulate the classical model, which was subsequently generalized using the fractal–fractional derivative operator. Many researchers and scientists use different numerical tools to solve fractional differential equations. Few techniques are used to solve these different types of fractional differential equations representing different physical phenomena. The Atangana-Baleanu fractional operator was used to assess and research the polio model and its related work30. The Picard-Lindelöf theorem was used to establish the prerequisites for the suggested model’s existence of a singular solution. The fractional-order system was numerically solved using a unique approximation strategy based on the Adams-Bashforth method. Researchers proposed a novel fractional order measles model in31, which utilized a constant proportional (CP) Caputo operator to explore and observe the dynamic transmission of the disease under the influence of vaccination. They numerically modeled a set of fractional differential equations using the Laplace with the Adomian decomposition technique.

The objective of this study is to create a fractal–fractional model utilizing the Mittag-Leffler kernel to elucidate COVID-19 transmission among a population with diabetes as an underlying condition. The model focuses on the transmission of COVID-19 solely between humans in a community where diabetes is a prevalent underlying disease.

Section (1) consists of the introduction and literature review to see the historical background as well as applications. The basic preliminaries are given in Section (2), which will help find reliable solutions to the fractional order system. Mathematical fractional order models with analysis like positivity and quantitative and qualitative analysis are studied in Section (3), including stability analysis. The fractional-fractional operator is used to find the reliable solution in Section (4). The results and discussion of the simulation and its physical interpretation are verified in Section (5). The paper’s overall conclusion is provided in Section (6).

Basic definitions

Definition 2.1

20,21,24 For a power law kernel, the fractal–fractional derivative in the Riemann-Liouville sense with order \(0 \le \alpha , \beta \le 1\) is defined as:

$$\begin{aligned} {}_0^{FFP} {D}_t^{\alpha , \beta } y(t) = \frac{1}{\Gamma (1-\alpha )} \frac{d}{dt^\beta } \int _0^t y(\tau ) (t-\tau )^{-\alpha } d\tau , \end{aligned}$$
(1)

where

$$\begin{aligned} \frac{dy(t)}{dt^{\beta }} = \lim _{t \rightarrow t_1} \frac{y(t) - D(t_1)}{t^{2-\beta }-{t_1}^{2-\beta }}. \end{aligned}$$
(2)

The associated fractal–fractional integral is expressed as follows:

$$\begin{aligned} _0^{FFP} I ^{\alpha ,\beta } y(t)= \frac{1}{\Gamma (\alpha )} \int ^t_0 (t-\tau )^{\alpha -1} \tau ^{1-\beta }y(\tau ) d\tau . \end{aligned}$$
(3)

Definition 2.2

20,21,24 For an exponential decay kernel, the fractal–fractional derivative in the Riemann-Liouville sense with order \(0 \le \alpha , \beta \le 1\) is defined as:

$$\begin{aligned} {}_{0}^{FFE}{D}_{t}^{\alpha ,\beta } y(t) = \frac{M(\alpha )}{\Gamma (1-\alpha )} \frac{d}{dt^\beta }\int ^{t}_0 \exp \Big [-\frac{\alpha }{1-\alpha } (t-\tau )^{-\alpha }\Big ] y(\tau )d\tau , \end{aligned}$$
(4)

where \(\alpha >0, \beta \le n \in N\), and \(M(0)=1=M(1)\).

The associated integral is given by

$$\begin{aligned} _0^{FFE} I ^{\alpha ,\beta } y(t)= \frac{\beta (1-\alpha ) t^{\beta -1} y(t)}{M(\alpha )}+\frac{\alpha \beta }{M(\alpha )} \int ^t_0 \tau ^{\alpha -1} y(\tau ) d\tau . \end{aligned}$$
(5)

Definition 2.3

20,21,24 For a Mittag-Leffler kernel, the fractal–fractional derivative in the Riemann-Liouville sense with order \(0 \le \alpha , \beta \le 1\) is defined as:

$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta } y(t) = \frac{AB(\alpha )}{1-\alpha } \frac{d}{dt^\beta } \int _0^t y(\tau ) E_{\alpha } \big [- \frac{\alpha }{1-\alpha }(t-\tau )^{\alpha } \big ] d\tau , \end{aligned}$$
(6)

where \(0 < \alpha , \beta \le 1\), \(E_\alpha\) is the Mittag-Leffler function and \(AB(\alpha )=1-\alpha +\frac{\alpha }{\Gamma (\alpha )}\) is a normalization function.

The corresponding integral is given by

$$\begin{aligned} {}_0^{FFM} {I}^{\alpha , \beta } y(t)= \frac{1-\alpha }{AB(\alpha )} t^{1-\beta } y(t) + \frac{\alpha }{AB(\alpha )\Gamma (\alpha )} \int _0^t (t-\tau )^{\alpha -1} \tau ^{1-\beta } y(\tau ) d\tau . \end{aligned}$$
(7)

COVID-19 model with diabetes with fractional operator

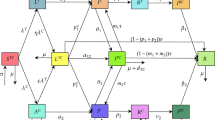
We will be discussing a model, which was introduced in7, that aims to elucidate COVID-19 transmission among a population with diabetes as an underlying condition. The entire community is classified into six distinct categories: S(t) represents susceptible individuals, D(t) denotes susceptible individuals with diabetes, E(t) represents individuals who have been exposed to COVID-19, I(t) represents individuals who have been infected with COVID-19, C(t) denotes COVID-19 cases with diabetes, and R(t) represents individuals who have recovered from COVID-19 or have been removed from the susceptible population.

Assumptions:

  • We suppose that there are no restrictions on age, mobility, or other social variables and that the population is evenly distributed.

  • Every infant is vulnerable.

  • When individuals classified as vulnerable come into contact with individuals in the (I) or (C) category, there is a possibility of infection. The infected person then transitions to the (E) category, representing exposure to the illness.

  • Those with diabetes who contract COVID-19 recover from it at a rate of \(\gamma _1\), while those without diabetes recover at a rate of \(\gamma\).

The fractal–fractional derivative is helpful in practical issues to improve memory effects system modeling. Hence, we provide an extension of the previous model7 utilizing the Mittag-Leffler core and the fractal–fractional function as follows:

$$\begin{aligned}{} & {} {}_0^{FFM} {D}_t^{\alpha , \beta } S(t) = \Omega - \beta \left( \frac{I+C}{N}\right) S - (\nu +\lambda )S, \nonumber \\{} & {} {}_0^{FFM} {D}_t^{\alpha , \beta } D(t) = \lambda S + \gamma _1 C - \beta \left( \frac{I+C}{N}\right) D - (\delta _2 + \nu )D, \nonumber \\{} & {} {}_0^{FFM} {D}_t^{\alpha , \beta } E(t) = \beta \left( \frac{I+C}{N}\right) S + \beta \left( \frac{I+C}{N}\right) D - (\phi +\nu )E, \nonumber \\{} & {} {}_0^{FFM} {D}_t^{\alpha , \beta } I(t) = \alpha \phi E - (\delta + \nu + \gamma ) I, \nonumber \\{} & {} {}_0^{FFM} {D}_t^{\alpha , \beta } C(t) = (1-\alpha ) \phi E - (\delta _1 + \nu ) C, \nonumber \\{} & {} {}_0^{FFM} {D}_t^{\alpha , \beta } R(t) = \gamma I - \nu R. \end{aligned}$$
(8)

Subjected to initial conditions:

$$\begin{aligned} S(0)\ge 0, \ \ D(0)\ge 0, \ \ E(0)\ge 0, \ \ I(0)\ge 0, \ \ C(0)\ge 0, \ \ R(0)\ge 0. \end{aligned}$$
(9)

where \(0 < \alpha , \beta \le 1\).

By using the substitute of fractal fractional operator (definition 2.3 equation number (7)), in which \(\alpha\) is the fractional derivative function while \(\beta\) represents its dimensions.

Non-negative bounded solutions

Theorem 3.1

32,33 In straight-line requirement, the proposed framework’ suggested solution is non-negative and restricted in \(R_{+}^{6}\).

Proof

It is necessary to demonstrate that there is a vector field point \(R_{+}^{6}\) on each hyper-plane bounded by the positive orthant in order to demonstrate that the model’s solution is nonnegative. We have got

$$\begin{aligned} {D}_t^{\alpha , \beta } S(t)\mid _{S=0}= & {} \Omega \ge 0,\nonumber \\ {D}_t^{\alpha , \beta } D(t)\mid _{D=0}= & {} \lambda S + \gamma _1 C \ge 0,\nonumber \\ {D}_t^{\alpha , \beta } E(t)\mid _{E=0}= & {} \beta \left( \frac{I+C}{N}\right) S + \beta \left( \frac{I+C}{N}\right) D \ge 0,\nonumber \\ {D}_t^{\alpha , \beta } I(t)\mid _{I=0}= & {} \alpha \phi E \ge 0,\nonumber \\ {D}_t^{\alpha , \beta } C(t)\mid _{C=0}= & {} (1-\alpha ) \phi E \ge 0,\nonumber \\ {D}_{t}^{\alpha , \beta } R(t)\mid _{R=0}= & {} \gamma I \ge 0. \end{aligned}$$
(10)

The solution is restricted to a hyperplane and will not be able to escape it if \((S(0), D(0), E(0), I(0), C(0), R(0)) \epsilon R_{+}^{6}\). The domain \(R_{+}^{6}\) refers to a positivity invariant set in which every hyperplane’s vector field constantly points in the direction of the non-negative orthant, encapsulating it inside its boundaries. \(\square\)

Effect of global derivative and existence of unique solutions

The Riemann-Stieltjes integral is a widely used type of integral that includes the classical integral as a specific example, which has been well-established in the literature. We’ll apply this concept to investigate its possible influence on the exogenous growth model in this section. To do this, we shall substitute the global derivative for the standard derivative. Let’s assume that function g is differentiable. Consequently,

$$\begin{aligned} S'= & {} g'\left[ \Omega - \beta (\frac{I+C}{N})S - (\nu +\lambda )S\right] = J_1(t,\xi ), \nonumber \\ D'= & {} g'\left[ \lambda S + \gamma _1 C - \beta \left( \frac{I+C}{N}\right) D - (\delta _2 + \nu )D\right] = J_2(t,\xi ), \nonumber \\ E'= & {} g'\left[ \beta \left( \frac{I+C}{N}\right) S + \beta \left( \frac{I+C}{N}\right) D - (\phi +\nu )E\right] = J_3(t,\xi ), \nonumber \\ I'= & {} g'\left[ \alpha \phi E - (\delta + \nu + \gamma ) I\right] = J_4(t,\xi ),\nonumber \\ C'= & {} g'\left[ (1-\alpha ) \phi E - (\delta _1 + \nu ) C\right] = J_5(t,\xi ), \nonumber \\ R'= & {} g'[\gamma I - \nu R] = J_6(t,\xi ). \end{aligned}$$
(11)

Where

$$\begin{aligned} \xi = S,D,E,I,C, R \end{aligned}$$
(12)

By selecting an appropriate function for g(t), a specific procedure can be established. For instance, choosing \(g(t) = t^{\alpha }\), where \(\alpha \in \mathbb {R}\), would result in a fractal behavior. However, this is subject to the following conditions:

$$\begin{aligned} \parallel {g'} \parallel _{\infty }= \sup _{t \in D^{'}_{g}} < N. \end{aligned}$$
(13)

From equation (13), it can be observed that the system of equations has a unique solution. However, this is subject to the verification of the following two conditions:

  • \(\mid J(t,S,D,E,I,C,R) < \kappa (1+|S|^2) \mid\)

  • \(\forall S_1, S_2\) we have \(\Vert J(t,S_1,D,E,I,C,R) - J(t,S_2,D,E,I,C,R) \Vert < {\kappa \Vert S_1 - S_2 \Vert ^{2}_{\infty }}\).

Initially,

$$\begin{aligned} |J_1(t,S_1,D,E,I,C,R)|^2= & {} |g'[\Omega - \beta (\frac{I+C}{N})S - (\mu +\lambda )S]|^2\nonumber \\\le & {} 2|g'|^2 \left[ |\Omega |^2 + |- \beta \left( \frac{I+C}{N}\right) - (\nu +\lambda )|^2 |S|^2 \right] \nonumber \\\le & {} 2|g'|^2\left( |\Omega |^2 + \left( |2 \frac{\beta ^2}{N^2} |{I+C}| + 2\left( \nu + \lambda \right) ^2\right) \right) |S|^2 \nonumber \\\le & {} 2|g'|^2 |\Omega |^2 (1 + \frac{(|2 \frac{\beta ^2}{N^2} |{I+C}| + 2( \nu + \lambda )^2))|S|^2}{\Omega ^2}) \nonumber \\< & {} \kappa _1 (1+|S|^2) \mid , \end{aligned}$$
(14)

under the condition

$$\begin{aligned} \frac{(|2 \frac{\beta ^2}{N^2} |{I+C}| + 2( \nu + \lambda )^2))|S|^2}{\Omega ^2} < 1, \end{aligned}$$
(15)

where

$$\begin{aligned} \kappa _1= & {} 2|g'|^2 |\Omega |^2. \end{aligned}$$
(16)
$$\begin{aligned} |J_2(t,S_1,D,E,I,C,R)|^2= & {} |g'[\lambda S + \gamma _1 C - \beta \left( \frac{I+C}{N}\right) D - (\delta _2 + \nu )D]|^2 \nonumber \\ {}\le & {} |g'|^2 [|\lambda S + \gamma _1 C - \beta (\frac{I+C}{N})D - (\delta _2 + \nu )|D]|^2 \nonumber \\ {}\le & {} |g'|^2 [ |(2\lambda S + \gamma _1 C)|^2 + |\left( \beta \left( \frac{I+C}{N}\right) - (\delta _2 + \nu )\right) |^2|D|^2] \nonumber \\ {}\le & {} |g'|^2 [ (\lambda ^2 |S|^2 + 2 \gamma _{1}^{2} |C|^2) + ( \frac{4\beta ^2}{N} |({I+C})|^2 + (2(\delta _2 + \nu )^2)|D|^2 \nonumber \\\le & {} |g'|^2 (\lambda ^2 |S|^2 + 2 \gamma _1^2 |C|^2)( 1 + \frac{( \frac{4\beta ^2}{N} |({I+C})|^2 + (2(\delta _2 + \nu )^2)|D|^2)}{(\lambda ^2 |S|^2 + 2 \gamma _1^2 |C|^2)} \nonumber \\< & {} \kappa _2 (1+|D|^2)) \mid , \end{aligned}$$
(17)

under the condition

$$\begin{aligned} \frac{( \frac{4\beta ^2}{N} |({I+C})|^2 + (2(\delta _2 + \nu )^2)|D|^2)}{(\lambda ^2 |S|^2 + 2 \gamma _1^2 |C|^2)} < 1, \end{aligned}$$
(18)

where

$$\begin{aligned} \kappa _2= & {} |g'|^2 (\lambda ^2 |S|^2 + 2 \gamma _1^2 |C|^2). \end{aligned}$$
(19)
$$\begin{aligned} \left| J_3(t,S_1,D,E,I,C,R)\right| ^2= & {} \left| g'\left[ \beta \left( \frac{I+C}{N}\right) S + \beta \left( \frac{I+C}{N}\right) D - (\phi + \mu )E\right] \right| ^2\nonumber \\\le & {} 2|g'|^2 \frac{\beta ^2}{N^2} |(I+C)|^2 |S+D|^2 + 2(\phi +\nu )^2|E|^2) \nonumber \\\le & {} 4|g'|^2 \frac{\beta ^2}{N^2} (|I|^2 + |C|^2) (|S|^2+ |D|^2) \left( 1 + \frac{2(\phi + \nu )^2|E|^2}{\frac{\beta ^2}{N^2} (|I|^2 + |C|^2) (|S|^2+ |D|^2)}\right) \nonumber \\< & {} \kappa _3 (1+|E|^2) \mid , \end{aligned}$$
(20)

under the condition

$$\begin{aligned} \frac{2(\phi +\nu )^2|E|^2}{\frac{\beta ^2}{N^2} (|I|^2 + |C|^2) (|S|^2+ |D|^2)} < 1, \end{aligned}$$
(21)

where

$$\begin{aligned} \kappa _3= & {} 4|g'|^2 \frac{\beta ^2}{N^2} (|I|^2 + |C|^2) (|S|^2+ |D|^2). \end{aligned}$$
(22)
$$\begin{aligned} |J_4(t,S_1,D,E,I,C,R)|^2= & {} {|g'[\alpha \phi E - (\delta + \nu + \gamma ) I]|}^2 \nonumber \\\le & {} |g'|^2 [(2\alpha ^2 \phi ^2 |E|^2)+ 2 (\delta + \nu + \gamma )^2 |I|^2 ] \nonumber \\\le & {} 2|g'|^2 \alpha ^2 \phi ^2 |E|^2) ( 1 + \frac{2 (\delta + \nu + \gamma )^2 |I|^2}{ \alpha ^2 \phi ^2 |E|^2)} \nonumber \\\le & {} \kappa _4 (1+|I|^2) \mid , \end{aligned}$$
(23)

under the condition

$$\begin{aligned} \frac{2 (\delta + \nu + \gamma )^2 |I|^2}{ \alpha ^2 \phi ^2 |E|^2)} < 1, \end{aligned}$$
(24)

where

$$\begin{aligned} \kappa _4= & {} 2|g'|^2 \alpha ^2 \phi ^2 |E|^2. \end{aligned}$$
(25)
$$\begin{aligned} |J_5(t,S_1,D,E,I,C,R)|^2= & {} {|g'[(1-\alpha ) \phi E - (\delta _1 + \nu ) C]}|^2 \nonumber \\ {}\le & {} g'|[((1-\alpha )^2 \phi ^2 |E|^2) + 2 (\delta _1 + \nu )^2 |C|^2 \nonumber \\\le & {} g'((1-\alpha )^2 \phi ^2 |E|^2)( 1 + \frac{2(\delta _1 + \nu )^2 |C|^2}{((1-\alpha )^2 \phi ^2 |E|^2)} \nonumber \\< & {} \kappa _1 (1+|C|^2) \mid , \end{aligned}$$
(26)

under the condition

$$\begin{aligned} \frac{2(\delta _1 + \nu )^2 |C|^2}{((1-\alpha )^2 \phi ^2 |E|^2)} < 1, \end{aligned}$$
(27)

where

$$\begin{aligned} \kappa _5= & {} g'((1-\alpha )^2 \phi ^2 |E|^2). \end{aligned}$$
(28)
$$\begin{aligned} |J_6(t,S_1,D,E,I,C,R)|^2= & {} |g'[\gamma I - \nu R]^2\nonumber \\\le & {} 2|g'|^2\left[ \gamma ^2 |I|^2 + 2 \mu ^2 |R|^2\right] \nonumber \\\le & {} 2|g'|^2\gamma ^2 |I|^2\left[ 1 + \frac{ 2 \nu ^2 |R|^2}{\gamma ^2 |I|^2}\right] \nonumber \\< & {} \kappa _6 (1+|R|^2) \mid , \end{aligned}$$
(29)

under the condition

$$\begin{aligned} \frac{2 \nu ^2 |R|^2}{\gamma ^2 |I|^2}] < 1, \end{aligned}$$
(30)

where

$$\begin{aligned} \kappa _6 = 2|g'|^2\gamma ^2 |I|^2. \end{aligned}$$
(31)

Hence it satisfies the linear growth condition. Additionally, we can verify the Lipschitz condition as follows:

$$\begin{aligned} |J_1(t,S_1,D,E,I,C,R)- J_1(t,S_2,D,E,I,C,R)|^2= & {} {\left| -\beta \frac{I+C}{N} - (\nu + \lambda )\right| }^2 {|(S_1-S_2)|}^2\nonumber \\\le & {} 2 {|\beta \frac{I+C}{N}|}^2 + 2 |(\nu + \lambda )|^2 |(S_1-S_2)|^2 \nonumber \\ {}\le & {} \frac{ 4 \beta ^2}{N^2}(|I|^2+|C|^2) + 4 (\nu ^2 + \lambda ^2) |(S_1-S_2)|^2 \nonumber \\\le & {} \frac{4 \beta ^2}{N^2}( \sup _{D \in I} |I|^2+ \sup _{t \in D_C}|C|^2) + 4 (\nu ^2 + \lambda ^2) \sup _{t \in D_S}|(S_1-S_2)|^2 \nonumber \\ {}\le & {} \frac{4 \beta ^2}{N^2} (\Vert I \Vert _{\infty }^{2} + \Vert C \Vert _{\infty }^{2} + 4 (\nu ^2 + \lambda ^2)) \Vert S_1 - S_2 \Vert ^{2}_{\infty } \nonumber \\\le & {} \bar{\kappa _1} \Vert S_1 - S_2 \Vert ^{2}_{\infty }, \end{aligned}$$
(32)

where

$$\begin{aligned} \bar{\kappa _1}= & {} \frac{4 \beta ^2}{N^2} (\Vert I \Vert _{\infty }^{2} + \Vert C \Vert _{\infty }^{2} + 4 (\nu ^2 + \lambda ^2)). \end{aligned}$$
(33)
$$\begin{aligned} |J_2(t,S,D_1,E,I,C,R)- J_2(t,S,D_2,E,I,C,R)|^2= & {} {\left| -\beta \frac{I+C}{N} - ( \delta _2 + \nu )\right| }^2 {|(D_1- D_2)|}^2 \nonumber \\\le & {} \frac{2 \beta ^2}{N^2} {|{I+C}|}^2 + 2 |(\delta _2 + \nu )|^2 |(D_1-D_2)|^2 \nonumber \\\le & {} \frac{ 4 \beta ^2}{N^2}(|I|^2+|C|^2) + 2 (\delta _2 + \nu )^2 |(D_1-D_2)|^2 \nonumber \\\le & {} (\frac{4 \beta ^2}{N^2}( \sup _{t \in D_I} |I|^2+ \sup _{t \in D_C}|C|^2) + 2 (\delta _2 + \nu )^2) \sup _{t \in D}|(D_1- D_2)|^2 \nonumber \\ {}\le & {} \frac{4 \beta ^2}{N^2} (\Vert I \Vert _{\infty }^{2} + \Vert C \Vert _{\infty }^{2} + 2 (\delta _2 + \nu )^2) \Vert D_1 - D_2 \Vert ^{2}_{\infty } \nonumber \\ {}\le & {} \bar{\kappa _2} \Vert D_1 - D_2 \Vert ^{2}_{\infty }, \end{aligned}$$
(34)

where

$$\begin{aligned} \bar{\kappa _2}= & {} \frac{4 \beta ^2}{N^2} (\Vert I \Vert _{\infty }^{2} + \Vert C \Vert _{\infty }^{2} + 2 (\delta _2 + \mu )^2). \end{aligned}$$
(35)
$$\begin{aligned} |J_3(t,S,D,E_1,I,C,R)- J_3(t,S,D,E_2,I,C,R)|^2= & {} {|- (\phi +\nu ) |}^2 {| E_1 - E_2 |}^{2} \nonumber \\ {}\le & {} ((\phi +\nu )^2 + \epsilon ) | E_1 - E_2 |^{2} \nonumber \\ {}\le & {} ((\phi + \nu )^2 + \epsilon ) \sup _{t \in D_E} {| E_1 - E_2 |}^{2} \nonumber \\ {}\le & {} ((\phi +\nu )^2 + \epsilon ) {\sup }_{t \in D_E} { \Vert {E_1 - E_2} \Vert }_{\infty }^{2} \nonumber \\ {}\le & {} \bar{\kappa _3} {\Vert E_1 - E_2 \Vert }^{2}_{\infty } \end{aligned}$$
(36)

, where

$$\begin{aligned} \bar{\kappa _3}= & {} ((\phi +\mu )^2 + \epsilon ). \end{aligned}$$
(37)
$$\begin{aligned} |J_4(t,S,D,E,I_1,C,R)- J_4(t,S,D,E,I_2,C,R)|^2= & {} |- (\delta + \nu + \gamma ) |^2 | I_1 - I_2 |^{2} \nonumber \\ {}\le & {} ((\delta + \nu + \gamma )^2 + \epsilon ) | I_1 - I_2 |^{2} \nonumber \\ {}\le & {} ((\delta + \nu + \gamma )^2 + \epsilon ) \sup _{t \in D_I} | I_1 - I_2 |^{2} \nonumber \\\le & {} ((\delta + \nu + \gamma )^2 + \epsilon ) \sup _{t \in D_I} \Vert I_1 - I_2 \Vert ^{2}_{\infty } \nonumber \\ {}\le & {} \bar{\kappa _4} \Vert I_1 - I_2 \Vert ^{2}_{\infty }, \end{aligned}$$
(38)

where

$$\begin{aligned} \bar{\kappa _4}= & {} ((\delta + \mu + \gamma )^2 + \epsilon ). \end{aligned}$$
(39)
$$\begin{aligned} |J_5(t,S,D,E,I,C_1,R)- J_5(t,S,D,E,I,C_2,R)|^2= & {} |- (\delta _1 +\nu ) |^2 | C_1 - C_2 |^{2}\nonumber \\ {}\le & {} ((\delta _1+ \nu )^2 + \epsilon ) | C_1 - C_2 |^{2} \nonumber \\ {}\le & {} ((\delta _1+\nu )^2 + \epsilon ) \sup _{t \in D_C} | C_1 - C_2 |^{2} \nonumber \\ {}\le & {} ((\delta _1+\nu )^2 + \epsilon ) \sup _{t \in D_C} \Vert C_1 - C_2 \Vert ^{2}_{\infty } \nonumber \\\le & {} \bar{\kappa _5} \Vert C_1 - C_2 \Vert ^{2}_{\infty }, \end{aligned}$$
(40)

where

$$\begin{aligned} \bar{\kappa _5}= & {} ((\delta _1+\mu )^2 + \epsilon ). \end{aligned}$$
(41)
$$\begin{aligned} |J_6(t,S,D,E,I,C,R_1)- J_6(t,S,D,E,I,C,R_2)|^2= & {} |- \nu |^2 | R_1 - R_2 |^{2} \nonumber \\ {}\le & {} ( \nu ^2 + \epsilon ) | R_1 - R_2 |^{2} \nonumber \\ {}\le & {} ( \nu ^2 + \epsilon ) \sup _{t \in D_R} | R_1 - R_2 |^{2} \nonumber \\ {}\le & {} ( \nu ^2 + \epsilon ) \sup _{t \in D_R} \Vert R_1 - R_2 \Vert ^{2}_{\infty } \nonumber \\ {}\le & {} \bar{\kappa _6} \Vert R_1 - R_2 \Vert ^{2}_{\infty }, \end{aligned}$$
(42)

where

$$\begin{aligned} \bar{\kappa _6} = ( \nu ^2 + \epsilon ). \end{aligned}$$
(43)

Hence, the singularity of the exact solution for each product, the corresponding linear growth, and the Lipschitz criteria are satisfied for the feasible solution of the model.

Equilibrium points analysis

In this subsection, the equilibrium points for endemic and disease-free conditions are identified. The right-hand side of the system is equal to zero, which yields the equilibrium point. Using system (8), the disease-free equilibrium point \((E_0)\) is

$$\begin{aligned} E_0 = (S^0, D^0, E^0, I^0, C^0, R^0) = \Big ( \frac{\Omega }{\nu +\lambda }, \frac{\Omega \lambda }{(\delta _2+\nu )(\nu +\lambda ))}, 0, 0, 0, 0 \Big ). \end{aligned}$$
(44)

The endemic equilibrium point \((E_1)\) is7:

$$\begin{aligned} E_1 = (S^*, D^*, E^*, I^*, C^*, R^*)= {\left\{ \begin{array}{ll} S^* = \frac{\Omega }{\beta (I^* + C^*)/(N+(\nu +\lambda )}, \\ D^* = \frac{\lambda S^* + \gamma _1 C^*}{\beta (I^* + C^*)/(N+(\nu +\delta _2)},\\ E^* = \frac{\beta }{(\phi +\nu )} \Big [ \frac{(I^* +C^*)(S^*+D^*)}{N} \Big ], \\ {I}^* = \frac{\alpha \phi E^*}{(\delta +\nu + \gamma )}, \\ {C}^* = \frac{(1-\alpha )\phi E^*}{(\delta _1+\nu +\gamma _1)}, \\ R^* = \frac{\gamma I^*}{\nu }. \end{array}\right. } \end{aligned}$$
(45)

Reproduction number

A key idea in epidemic models is the basic reproduction number, which represents the anticipated number of secondary infected cases that a primary infected case is predicted to create over the course of the whole infectiousness period. It facilitates the formulation of immunization programs and, in the event that the number of cases exceeds 1, can immediately put a stop to the epidemic. The reproductive number is derived using Next generation Matrix method34, which is the verge condition of the epidemic system from which we decide that our system is either in the disease-free state or in the endemic state depending on the value of \(R_{0}\).

  • If \(R_{0}<1\) the system is disease free whereas

  • if \(R_{0}>1\) then our proposed system is in endemic state.

As stated in7, we get the basic reproductive number \((R_{0})\):

$$\begin{aligned} R_0 = \sqrt{\beta \alpha \phi ( \phi + \nu ) (\delta + \nu + \gamma )\left( \frac{\Omega ( \lambda + \delta _2 + \mu )}{(\nu + \lambda )(\delta _2 + \nu )} \right) + (1-\alpha )\phi } \end{aligned}$$
(46)

Sensitivity analysis of model

This analysis aids in determining the sensitivity of the reproductive number, \(R_0\), by calculating the partial derivatives of the pertinent parameters that impact the threshold:

$$\begin{aligned} \frac{\partial R_0}{\partial \beta }= & {} \frac{\alpha \phi ( \phi + \nu ) (\delta +1 + \nu + \gamma )\left( \frac{\Omega ( \lambda + \delta _2 + \nu )}{(\nu + \lambda )(\delta _2 + \nu )} \right) }{ \Game } > 0, \end{aligned}$$
(47)
$$\begin{aligned} \frac{\partial R_0}{\partial \alpha }= & {} \frac{\beta \phi ( \phi + \nu ) (\delta + \nu + \gamma )\left( \frac{\Omega ( \lambda + \delta _2 + \nu )}{(\nu + \lambda )(\delta _2 + \nu )} \right) -\phi }{\Game } > 0, \end{aligned}$$
(48)
$$\begin{aligned} \frac{\partial R_0}{\partial \phi }= & {} \frac{\beta \alpha ( 2 \phi + \nu ) (\delta + \nu + \gamma )\left( \frac{\Omega ( \lambda + \delta _2 + \nu )}{(\nu + \lambda )(\delta _2 + \nu )} \right) + (1-\alpha )}{\Game } > 0, \end{aligned}$$
(49)
$$\begin{aligned} \frac{\partial R_0}{\partial \nu }= & {} \frac{ \nabla }{\Game } > 0, \end{aligned}$$
(50)
$$\begin{aligned} \frac{\partial R_0}{\partial \delta _1}= & {} \frac{\beta \alpha \phi ( \phi + \nu )\left( \frac{\Omega ( \lambda + \delta _2 + \nu )}{(\nu + \lambda )(\delta _2 + \nu )} \right) }{\Game } > 0, \end{aligned}$$
(51)
$$\begin{aligned} \frac{\partial R_0}{\partial \gamma }= & {} \frac{\beta \alpha \phi ( \phi + \nu )\left( \frac{\Omega ( \lambda + \delta _2 + \nu )}{(\nu + \lambda )(\delta _2 + \nu )} \right) }{\Game } > 0, \end{aligned}$$
(52)
$$\begin{aligned} \frac{\partial R_0}{\partial \Omega }= & {} \frac{\beta \alpha \phi ( \phi + \nu ) (\delta + \nu + \gamma )\left( \frac{( \lambda + \delta _2 + \nu )}{(\nu + \lambda )(\delta _2 + \mu )} \right) }{\Game } > 0, \end{aligned}$$
(53)
$$\begin{aligned} \frac{\partial R_0}{\partial \lambda }= & {} - \frac{\beta \alpha \phi ( \phi + \nu ) (\delta + \nu + \gamma )\left( \frac{\Omega }{(\nu + \lambda )^2(\delta _2 + \nu )}\right) }{\Game } < 0, \end{aligned}$$
(54)
$$\begin{aligned} \frac{\partial R_0}{\partial \delta _2}= & {} - \frac{\beta \alpha \phi ( \phi + \nu ) (\delta + \nu + \gamma )\left( \frac{\Omega }{(\nu + \lambda )(\delta _2 + \nu )^2} \right) }{\Game } < 0. \end{aligned}$$
(55)

Where

$$\begin{aligned} \Game= & {} 2\left[ \sqrt{\beta \alpha \phi ( \phi + \nu ) (\delta _1 + \nu + \gamma )( \frac{\Omega ( \lambda + \delta _2 + \nu )}{(\nu + \lambda )(\delta _2 + \nu )} )+ (1-\alpha )\phi }\right] , \end{aligned}$$
(56)
$$\begin{aligned} \nabla= & {} \frac{1}{(\nu + \lambda )^2(\delta _2 + \nu )^2} \Big [ \nu ^4 + 2\delta _2 \nu ^3 + 2 \lambda \nu ^3 + \delta _2^2 \nu ^2 + \lambda ^2 \nu ^2 + 5 \delta _2 \lambda \nu ^2 - \gamma \phi \nu ^2 - \delta _1 \phi \nu ^2 + 2 \delta _2 \lambda ^2 \nu + 2 \delta _2^2 \lambda \nu \nonumber \\{} & {} + 2 \gamma \lambda \delta _2 \nu + 2 \delta _2 \lambda \phi \nu + 2 \delta _1 \delta _2 \lambda \nu - 2 \gamma \delta _2 \phi \nu - 2 \gamma \lambda \phi \nu - 2 \delta _1 \lambda \phi \nu + \delta _1 \delta _2 \lambda ^2 + \delta _1 \delta _2^2 \lambda + \gamma \delta _2 \lambda ^2 + \gamma \delta _2^2 \lambda + \delta _2^2 \lambda \phi \nonumber \\{} & {} + \delta _2 \lambda ^2 \phi - \delta _1 \delta _2^2 \phi - \delta _1 \lambda ^2 \phi - \delta _1 \delta _2 \lambda \phi - \delta _1 \delta _2^2 \phi - \delta _1 \lambda ^2 \phi - \delta _1 \delta _2 \lambda \phi \Big ]. \end{aligned}$$
(57)

As we manipulate the parameters, it becomes apparent that \(R_0\) is highly sensitive. In this study, the parameters \(\beta\), \(\alpha\), \(\phi\), \(\nu\), \(\delta _1\), \(\gamma\), and \(\Omega\) increase, while \(\delta _2\) and \(\lambda\) decrease. Hence, it is advisable to prioritize preventive measures over treatment as a means of controlling the spread of infection.

Global stability analysis

Since differences in mathematical models can result in variability, stability is a critical component of dynamic systems and is necessary for both real-world control systems and physical application. Because stability qualities have so many potential uses, researchers are interested in studying them. In dynamical system stability and control theory, scalar functions known as Lyapunov functions are essential.

Lemma 3.2

35 Consider that the function \(\gamma (t)\in \mathbb {R}^{+}\) is differentiable. Then for \(\alpha ,\beta \in (0, 1)\),

$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta } \Big (\gamma -\gamma ^{*}-\gamma ^{*}\ln \frac{\gamma }{\gamma ^{*}}\Big ) \le \Big (1-\frac{\gamma ^{*}}{\gamma }\Big ) {}_0^{FFM} {D}_t^{\alpha , \beta }\gamma (t),~~~~~~~~\forall t\ge 0. \end{aligned}$$
(58)

Lyapunov’s first derivative for global stability

To establish the endemic Lyapunov function, we consider all the independent variables in our model, namely S, D, E, I, C, and R. For the harmful equilibrium \(E_1\), we set \(L<0\) to define the Lyapunov function.

Theorem 3.3

33 When the reproductive number \(R_0 > 1\), the harmful impact equilibrium points \(E_1\) (45) of the survival fractional calculus model exhibit global asymptotic stability. This indicates that the disease persists and does not lead to eradication.

Proof

We can express Lyapunov function as:

$$\begin{aligned} L\left( S^*,D^*,E^*,I^*,C^*,R^*\right)&= \left( S-S^*-S^* log \frac{S^*}{S}\right) +\left( D-D^*-D^* log \frac{D^*}{D}\right) +\left( E-E^*-E^* log \frac{E^*}{E}\right) \nonumber \\&\quad +\left( I^*-I^*-I^* log \frac{I^*}{I^*}\right) + \left( C^*-C^*-C^* log \frac{C^*}{C^*}\right) +\left( R-R^*-R^* log \frac{R^*}{R}\right) . \end{aligned}$$
(59)

Substituting equation (59) into system (8) and utilizing Lemma (3.2), we find

$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta }L\le & {} \left( \frac{S-S^*}{S}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }{S}+\left( \frac{D-D^*}{D}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }{D}+\left( \frac{E-E^*}{E}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }{E}\\{} & {} +\left( \frac{I-I^*}{I}\right) {{}_0^{FFM} {D}_t^{\alpha , \beta }{C}} + \left( \frac{C-C^*}{C}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }{C}+\left( \frac{R-R^*}{R}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }{R} \end{aligned}$$

writing their expressions for derivatives as follows;

$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta }L&\le \Big (\frac{S-S^*}{S}\Big ) \Big (\Omega - \beta \Big (\frac{I+C}{N}\Big )S - (\nu +\lambda )S\Big )+\Big (\frac{D-D^*}{D}\Big )\Big (\lambda S + \gamma _1 C - \beta (\frac{I+C}{N})D - (\delta _2 + \nu )D\Big )\nonumber \\&{}+(\frac{E-E^*}{E})\Big (\beta \Big (\frac{I+C}{N}\Big )S + \beta \Big (\frac{I+C}{N}\Big )D - (\phi +\nu )E\Big )+\Big (\frac{I-I^*}{I}\Big )\Big (\alpha \phi E - (\delta + \nu + \gamma ) I\Big )\nonumber \\&{}+ \Big (\frac{C-C^*}{C}\Big )\Big ((1-\alpha ) \phi E - (\delta _1 + \nu ) C\Big ) +\Big (\frac{R-R^*}{R}\Big )\Big (\gamma I - \nu R\Big ). \end{aligned}$$
(60)

Putting \(S=S-S^*\), \(D=D-D^*\), \(E=E-E^*\), \(I=I-I^*\), \(C=C-C^*\), \(R=R-R^*\), we find

$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta }L&\le \left( \frac{S-S^*}{S}\right) ( \Omega - \beta \left( \frac{(I-I^*)+(C-C^*)}{N}\right) (S-S^*) - (\nu +\lambda )(S-S^*) )+(\frac{D-D^*}{D})(\lambda (S-S^*) \nonumber \\&\quad + \gamma _1 (C-C^*) - \beta \left( \frac{(I-I^*)+(C-C^*)}{N}\right) (D-D^*) - (\delta _2 + \nu )(D-D^*)) + \left( \frac{E-E^*}{E}\right) \nonumber \\&\quad (\beta (\frac{(I-I^*)+(C-C^*)}{N})(S-S^*) + \beta \left( \frac{(I-I^*)+(C-C^*)}{N}\right) (D-D^*) - (\phi +\nu )(E-E^*)) \nonumber \\&\quad + \left( \frac{I-I^*}{I}\right) (\alpha \phi (E-E^*) - (\delta + \nu + \gamma )(I-I^*)) + \left( \frac{C-C^*}{C}\right) ((1-\alpha ) \phi (E-E^*) \nonumber \\&\quad - (\delta _1 + \nu ) (C-C^*))+\left( \frac{R-R^*}{R}\right) (\gamma (I-I^*) - \nu (R-R^*)), \end{aligned}$$
(61)

which can be written as:

$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta } L \le \aleph - \Re . \end{aligned}$$
(62)

It can be easily seen that if \(\aleph < \Re\) this yields \({}_0^{FFM} {D}_t^{\alpha , \beta }L < 0\); however

$$0 = \aleph - \Re$$

implies \(\frac{dL}{dt} = 0\) if \(S=S^*\), \(D=D^*\), \(E=E^*\), \(I=I^*\), \(C=C^*\), \(R=R^*\), So

$$\begin{aligned} \Big \{(S^*, D^*, E^*, I^*, C^*, R^*)\in \Gamma \, {}_0^{FFM} {D}_t^{\alpha , \beta }L=0\Big \}. \end{aligned}$$
(63)

is the point \(E_1\) the endemic equilibrium of the considered model. From Lasalle’s invariance concept, we can conclude that \(E_1\) is globally asymptotically stable in if \(\aleph < \Re\). \(\square\)

Second derivative of Lyapunov function for wave analysis

Further observations on each of the variations’ specifications are required because the first derivative evaluation of an arbitrary function cannot serve as a fully functional resource in displaying its variants. Consequently, we analyze the second derivative of the Lyapunov function associated with the system.

$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta }[{}_0^{FFM} {D}_t^{\alpha , \beta }L]=\ddot{L}\le & {} \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }S}{S}\right) ^2 {S^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }D}{D}\right) ^2 {D^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }E}{E}\right) ^2 {E^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }I}{I}\right) ^2 {I^*} \nonumber \\{} & {} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }C}{C}\right) ^2 {C^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }R}{R}\right) ^2 {R^*} + (1- \frac{S^*}{S}){}_0^{FFM} {D}_t^{\alpha , \beta }[{}_0^{FFM} {D}_t^{\alpha , \beta }S] \nonumber \\{} & {} + \left( 1- \frac{D^*}{D}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }\left[ {}_0^{FFM} {D}_t^{\alpha , \beta }D\right] +\left( 1- \frac{E^*}{E}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }\left[ {}_0^{FFM} {D}_t^{\alpha , \beta }E\right] \nonumber \\{} & {} + \left( 1- \frac{I^*}{I}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }[{}_0^{FFM} {D}_t^{\alpha , \beta }I] + \left( 1- \frac{C^*}{C}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }[{}_0^{FFM} {D}_t^{\alpha , \beta }C] \nonumber \\{} & {} + \left( 1- \frac{R^*}{R}\right) {}_0^{FFM} {D}_t^{\alpha , \beta }[{}_0^{FFM} {D}_t^{\alpha , \beta }R]. \end{aligned}$$
(64)

Then

$$\begin{aligned} \ddot{L}\le & {} \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }S}{S}\right) ^2 {S^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }D}{D}\right) ^2 {D^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }E}{E}\right) ^2 {E^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }I}{I}\right) ^2 {I^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }C}{C}\right) ^2 {C^*}\nonumber \\{} & {} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }R}{R}\right) ^2 {R^*} + \left( 1- \frac{S^*}{S}\right) \left( - \frac{\beta }{N}\left( \left( {}_0^{FFM} {D}_t^{\alpha , \beta }I + {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) S + \left( I+C\right) {}_0^{FFM} {D}_t^{\alpha , \beta }S\right) \right. \nonumber \\{} & {} \left. - \frac{\beta }{N}\left( \left( {}_0^{FFM} {D}_t^{\alpha , \beta }I + {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) D + \left( I+C\right) {}_0^{FFM} {D}_t^{\alpha , \beta } D\right) - \left( \delta _2 + \nu \right) {}_0^{FFM} {D}_t^{\alpha , \beta }D\right) + \left( 1- \frac{E^*}{E}\right) \nonumber \\{} & {} \left( \frac{\beta }{N}\left( \left( {}_0^{FFM} {D}_t^{\alpha , \beta }I + {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) S +\left( I+C\right) {}_0^{FFM} {D}_t^{\alpha , \beta }S\right) + \frac{\beta }{N}\left( \left( {}_0^{FFM} {D}_t^{\alpha , \beta }I+ {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) D \right. \right. \nonumber \\{} & {} \left. \left. + \left( I+C\right) {}_0^{FFM} {D}_t^{\alpha , \beta }D\right) - \left( \phi +\nu \right) {}_0^{FFM} {D}_t^{\alpha , \beta }E\right) + \left( 1- \frac{I^*}{I}\right) \left( \alpha \phi {}_0^{FFM} {D}_t^{\alpha , \beta }E - \left( \delta + \nu + \gamma \right) {}_0^{FFM} {D}_t^{\alpha , \beta }I \right) \nonumber \\{} & {} + \left( 1- \frac{C^*}{C}\right) \left( \left( 1-\alpha \right) \phi {}_0^{FFM} {D}_t^{\alpha , \beta }E- \left( \delta _1 + \nu \right) {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) + \left( 1- \frac{R^*}{R}\right) \left( \gamma {}_0^{FFM} {D}_t^{\alpha , \beta }I - \nu {}_0^{FFM} {D}_t^{\alpha , \beta }R\right) . \end{aligned}$$
(65)

Now let us consider that

$$\begin{aligned} {\dot{\Lambda }}\left( S,D,E,I,C,R\right)= & {} \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }S}{S}\right) ^2 {S^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }D}{D}\right) ^2 {D^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }E}{E}\right) ^2 {E^*} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }I}{I}\right) ^2 {I^*} \nonumber \\{} & {} + \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }C}{C}\right) ^2 {C^*}+ \left( \frac{{}_0^{FFM} {D}_t^{\alpha , \beta }R}{R}\right) ^2 {R^*}. \end{aligned}$$
(66)

Then

$$\begin{aligned} \ddot{L}\le & {} {\dot{\Lambda }}\left( S,D,E,I,C,R\right) + \left( 1- \frac{S^*}{S}\right) \left( - \frac{\beta }{N}\left( \left( {}_0^{FFM} {D}_t^{\alpha , \beta }I + {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) S + \left( I+C\right) {}_0^{FFM} {D}_t^{\alpha , \beta }S\right) \right. \nonumber \\{} & {} \left. - \frac{\beta }{N}\left( \left( {}_0^{FFM} {D}_t^{\alpha , \beta }I + {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) D + \left( I+C\right) {}_0^{FFM} {D}_t^{\alpha , \beta } D\right) - \left( \delta _2 + \nu \right) {}_0^{FFM} {D}_t^{\alpha , \beta }D\right) + \left( 1- \frac{E^*}{E}\right) \nonumber \\{} & {} \left( \frac{\beta }{N}\left( \left( {}_0^{FFM} {D}_t^{\alpha , \beta }I + {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) S +\left( I+C\right) {}_0^{FFM} {D}_t^{\alpha , \beta }S\right) + \frac{\beta }{N}\left( \left( {}_0^{FFM} {D}_t^{\alpha , \beta }I+ {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) D \right. \right. \nonumber \\{} & {} \left. \left. + \left( I+C\right) {}_0^{FFM} {D}_t^{\alpha , \beta }D\right) - \left( \phi +\nu \right) {}_0^{FFM} {D}_t^{\alpha , \beta }E\right) + \left( 1- \frac{I^*}{I}\right) \left( \alpha \phi {}_0^{FFM} {D}_t^{\alpha , \beta }E - \left( \delta + \nu + \gamma \right) {}_0^{FFM} {D}_t^{\alpha , \beta }I \right) \nonumber \\{} & {} + \left( 1- \frac{C^*}{C}\right) \left( \left( 1-\alpha \right) \phi {}_0^{FFM} {D}_t^{\alpha , \beta }E- \left( \delta _1 + \nu \right) {}_0^{FFM} {D}_t^{\alpha , \beta }C\right) + \left( 1- \frac{R^*}{R}\right) \left( \gamma {}_0^{FFM} {D}_t^{\alpha , \beta }I - \nu {}_0^{FFM} {D}_t^{\alpha , \beta }R\right) . \end{aligned}$$
(67)

After replacing the values of first derivatives we get

$$\begin{aligned} \ddot{L}&\le {\dot{\Lambda }}(S,D,E,I,C,R) + \left( 1- \frac{S^*}{S}\right) \left( - \frac{\beta }{N}( ( (\alpha \phi E - (\delta + \nu + \gamma ) I) + ( (1-\alpha ) \phi E - (\delta _1 + \nu ) C))S + (I+C)\right. \nonumber \\&\left. (\Omega - \beta \left( \frac{I+C}{N}\right) S - (\nu +\lambda )S)) - (\nu +\lambda ) \left( \Omega - \beta \left( \frac{I+C}{N}\right) S - (\nu +\lambda )S\right) \right) + (1- \frac{D^*}{D})\left( \lambda (\Omega - \beta \left( \frac{I+C}{N}\right) S\right. \nonumber \\&\left. - (\nu +\lambda )S) + \gamma _1 ( (1-\alpha ) \phi E - (\delta _1 + \nu ) C) - \frac{\beta }{N}( ( (\alpha \phi E - (\delta + \nu + \gamma ) I) + ( (1-\alpha ) \phi E - (\delta _1 + \mu ) C))D \right. \nonumber \\&\left. + (I+C) (\lambda S + \gamma _1 C - \beta \left( \frac{I+C}{N}\right) D - (\delta _2 + \nu )D) ) - (\delta _2 + \nu ) (\lambda S + \gamma _1 C - \beta \left( \frac{I+C}{N}\right) D - (\delta _2 + \mu )D) \right) \nonumber \\&+ (1- \frac{E^*}{E})\left( \frac{\beta }{N}( ( (\alpha \phi E - (\delta + \nu + \gamma ) I) + ( (1-\alpha ) \phi E - (\delta _1 + \nu ) C))S + (I+C) (\Omega - \beta (\frac{I+C}{N})S ) \right. \nonumber \\&\left. - (\nu +\lambda )S)+\frac{\beta }{N}( ( (\alpha \phi E - (\delta + \nu + \gamma ) I) + ( (1-\alpha ) \phi E - (\delta _1 + \nu ) C))D + (I+C) (\lambda S + \gamma _1 C \right. \nonumber \\&\left. - \beta (\frac{I+C}{N})D - (\delta _2 + \mu )D) )-(\phi +\nu ) (\beta (\frac{I+C}{N})S + \beta (\frac{I+C}{N})D - (\phi +\nu )E)\right) + (1- \frac{I^*}{I})\left( \alpha \phi (\beta (\frac{I+C}{N})S\right. \nonumber \\&\left. + \beta (\frac{I+C}{N})D - (\phi +\nu )E ) - (\delta + \nu + \gamma ) (\alpha \phi E - (\delta + \nu + \gamma ) I) \right) + \left( 1- \frac{C^*}{C}\right) ((1-\alpha ) \phi (\beta (\frac{I+C}{N})S \nonumber \\&+ \beta (\frac{I+C}{N})D - (\phi +\nu )E) - (\delta _1 + \nu )( (1-\alpha ) \phi E - (\delta _1 + \nu ) C)) + (1- \frac{R^*}{R})(\gamma (\alpha \phi E - (\delta + \nu + \gamma ) I)\nonumber \\&- \mu (\gamma I - \nu R)) \end{aligned}$$
(68)

Which can be written as

$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta }[{}_0^{FFM} {D}_t^{\alpha , \beta }L]=\ddot{L}\le & {} \wp _1 - \wp _2 \end{aligned}$$
(69)

Where \(\wp _1\) and \(\wp _2\) represent the positive and negative terms respectively, in Equation (68).

It can be seen that

  • If \(\wp _1 > \wp _2\) then \(\ddot{L} > 0.\)

  • If \(\wp _1 < \wp _2\) then \(\ddot{L} < 0.\)

  • If If \(\wp _1 = \wp _2\) then \(\ddot{L} = 0.\)

Algorithmic evaluation with fractal fractional purpose

In this part, the proposed numerical COVID-19 representation, incorporating diabetes, is implemented using novel distinctive and innate operator. Instead of the traditional differential operator, the Mittag-Leffler core operator will be utilized. Additionally, the version with flexible order will be employed in the model.

We can write the system (8) as:

$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta } S(t)= & {} S_1(t,\xi ), \end{aligned}$$
(70)
$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta } D(t)= & {} D_1(t,\xi ),\end{aligned}$$
(71)
$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta } E(t)= & {} E_1(t,\xi ),\end{aligned}$$
(72)
$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta } I(t)= & {} I_1(t,\xi ),\end{aligned}$$
(73)
$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta } C(t)= & {} C_1(t,\xi ),\end{aligned}$$
(74)
$$\begin{aligned} {}_0^{FFM} {D}_t^{\alpha , \beta } R(t)= & {} R_1(t,\xi ). \end{aligned}$$
(75)

We have

$$\begin{aligned} S(t_{\delta +1})= & {} S_0 + \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } S_1(t_{\delta }, S(t_{\delta }), D(t_{\delta }), E(t_{\delta }), I(t_{\delta }), C(t_{\delta }), R(t_{\delta })) \nonumber \\ {}{} & {} + \hbar \sum _{\mu =2}^{\delta } \int _{t_{\mu }}^{t_{\mu +1}} S_1(\tau ,\xi ) \tau ^{1-\beta } (t_{\delta +1}-\tau )^{\alpha -1} d\tau , \end{aligned}$$
(76)
$$\begin{aligned} D(t_{\delta +1})= & {} D_0 + \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } D_1(t_{\delta }, S(t_{\delta }), D(t_{\delta }), E(t_{\delta }), I(t_{\delta }), C(t_{\delta }), R(t_{\delta })) \nonumber \\ {}{} & {} + \hbar \sum _{\mu =2}^{\delta } \int _{t_{\mu }}^{t_{\mu +1}} D_1(\tau ,\xi ) \tau ^{1-\beta } (t_{\delta +1}-\tau )^{\alpha -1} d\tau , \end{aligned}$$
(77)
$$\begin{aligned} E(t_{\delta +1})= & {} E_0 + \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } E_1(t_{\delta }, S(t_{\delta }), D(t_{\delta }), E(t_{\delta }), I(t_{\delta }), C(t_{\delta }), R(t_{\delta })) \nonumber \\ {}{} & {} + \hbar \sum _{\mu =2}^{\delta } \int _{t_{\mu }}^{t_{\mu +1}} E_1(\tau ,\xi ) \tau ^{1-\beta } (t_{\delta +1}-\tau )^{\alpha -1} d\tau , \end{aligned}$$
(78)
$$\begin{aligned} I(t_{\delta +1})= & {} I_0 + \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } I_1(t_{\delta }, S(t_{\delta }), D(t_{\delta }), E(t_{\delta }), I(t_{\delta }), C(t_{\delta }), R(t_{\delta })) \nonumber \\ {}{} & {} + \hbar \sum _{\mu =2}^{\delta } \int _{t_{mu}}^{t_{\mu +1}} I_1(\tau ,\xi ) \tau ^{1-\beta } (t_{\delta +1}-\tau )^{\alpha -1} d\tau , \end{aligned}$$
(79)
$$\begin{aligned} C(t_{\delta +1})= & {} C_0 + \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } C_1(t_{\delta }, S(t_{\delta }), D(t_{\delta }), E(t_{\delta }), I(t_{\delta }), C(t_{\delta }), R(t_{\delta })) \nonumber \\ {}{} & {} + \hbar \sum _{\mu =2}^{\delta } \int _{t_{\mu }}^{t_{\mu +1}} C_1(\tau ,\xi ) \tau ^{1-\beta } (t_{\delta +1}-\tau )^{\alpha -1} d\tau , \end{aligned}$$
(80)
$$\begin{aligned} R(t_{\delta +1})= & {} R_0 + \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } R_1(t_{\delta }, S(t_{\delta }), D(t_{\delta }), E(t_{\delta }), I(t_{\delta }), C(t_{\delta }), R(t_{\delta }))\nonumber \\{} & {} + \hbar \sum _{\mu =2}^{\delta } \int _{t_{\mu }}^{t_{\mu +1}} R_1(\tau ,\xi ) \tau ^{1-\beta } (t_{\delta +1}-\tau )^{\alpha -1} d\tau . \end{aligned}$$
(81)

Where \(\xi = S,D,E,I,C,R\) and \(\hbar = \frac{\alpha }{AB(\alpha )\Gamma (\alpha )}\). we get,

$$\begin{aligned}{} & {} S^{\delta +1} = \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } S_1 (t_{\delta }, S^{\delta }, D^{^\delta }, E^{\delta }, I^{\delta }, C^{\delta }, R^{\delta })+ \frac{\alpha (\Delta t)^\mu }{AB(\alpha ) \Gamma (\alpha +1)} \nonumber \\{} & {} \quad \sum _{\mu =2}^{\delta } t_{\mu -2}^{1-\beta } S_1 (\Theta ) \times \Psi + \frac{\alpha (\Delta t)^\alpha }{AB(\alpha ) \Gamma (\alpha +2)} \sum _{\mu =2}^{\delta } \Big [ t_{\mu -1}^{1-\beta } S_1 (\mho ) - t_{\mu -2}^{1-\beta } S_1 (\theta ) \Big ] \times \Phi \nonumber \\{} & {} \quad + \frac{\alpha (\Delta t)^\alpha }{2AB(\alpha ) \Gamma (\alpha +3)} \sum _{\mu =2}^{\delta } [ t_{\mu }^{1-\beta } S_1 (t_{\mu }, S^{\mu }, D^{\mu }, E^{\mu }, I^{\mu }, C^{\mu }, R^{\mu })- 2t_{\mu -1}^{1-\beta } S_1 (\mho ) \nonumber \\{} & {} \quad - t_{\mu -2}^{1-\beta } S_1 (\Theta ) ] \times \zeta , \end{aligned}$$
(82)
$$\begin{aligned}{} & {} D^{\delta +1} = \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } D_1 (t_{\delta }, S^{\delta }, D^{^\delta }, E^{\delta }, I^{\delta }, C^{\delta }, R^{\delta })+ \frac{\alpha (\Delta t)^\mu }{AB(\alpha ) \Gamma (\alpha +1)} \nonumber \\{} & {} \quad \sum _{\mu =2}^{\delta } t_{\mu -2}^{1-\beta } D_1 (\Theta ) \times \Psi + \frac{\alpha (\Delta t)^\alpha }{AB(\alpha ) \Gamma (\alpha +2)} \sum _{\mu =2}^{\delta } \Big [ t_{\mu -1}^{1-\beta } D_1 (\mho ) - t_{\mu -2}^{1-\beta } D_1 (\theta ) \Big ] \times \Phi \nonumber \\{} & {} \quad + \frac{\alpha (\Delta t)^\alpha }{2AB(\alpha ) \Gamma (\alpha +3)} \sum _{\mu =2}^{\delta } [ t_{\mu }^{1-\beta } D_1 (t_{\mu }, S^{\mu }, D^{\mu }, E^{\mu }, I^{\mu }, C^{\mu }, R^{\mu })- 2t_{\mu -1}^{1-\beta } D_1 (\mho ) \nonumber \\{} & {} \quad - t_{\mu -2}^{1-\beta } D_1 (\Theta ) ] \times \zeta , \end{aligned}$$
(83)
$$\begin{aligned}{} & {} E^{\delta +1} = \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } E_1 (t_{\delta }, S^{\delta }, D^{^\delta }, E^{\delta }, I^{\delta }, C^{\delta }, R^{\delta })+ \frac{\alpha (\Delta t)^\mu }{AB(\alpha ) \Gamma (\alpha +1)} \nonumber \\{} & {} \quad \sum _{\mu =2}^{\delta } t_{\mu -2}^{1-\beta } E_1 (\Theta ) \times \Psi + \frac{\alpha (\Delta t)^\alpha }{AB(\alpha ) \Gamma (\alpha +2)} \sum _{\mu =2}^{\delta } \Big [ t_{\mu -1}^{1-\beta } E_1 (\mho ) - t_{\mu -2}^{1-\beta } E_1 (\theta ) \Big ] \times \Phi \nonumber \\{} & {} \quad + \frac{\alpha (\Delta t)^\alpha }{2AB(\alpha ) \Gamma (\alpha +3)} \sum _{\mu =2}^{\delta } [ t_{\mu }^{1-\beta } E_1 (t_{\mu }, S^{\mu }, D^{\mu }, E^{\mu }, I^{\mu }, C^{\mu }, R^{\mu })- 2t_{\mu -1}^{1-\beta } E_1 (\mho ) \nonumber \\{} & {} \quad - t_{\mu -2}^{1-\beta } E_1 (\Theta ) ] \times \zeta , \end{aligned}$$
(84)
$$\begin{aligned}{} & {} I^{\delta +1} = \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } I_1 (t_{\delta }, S^{\delta }, D^{^\delta }, E^{\delta }, I^{\delta }, C^{\delta }, R^{\delta })+ \frac{\alpha (\Delta t)^\mu }{AB(\alpha ) \Gamma (\alpha +1)} \nonumber \\{} & {} \quad \sum _{\mu =2}^{\delta } t_{\mu -2}^{1-\beta } I_1 (\Theta ) \times \Psi + \frac{\alpha (\Delta t)^\alpha }{AB(\alpha ) \Gamma (\alpha +2)} \sum _{\mu =2}^{\delta } \Big [ t_{\mu -1}^{1-\beta } I_1 (\mho ) - t_{\mu -2}^{1-\beta } I_1 (\theta ) \Big ] \times \Phi \nonumber \\{} & {} \quad + \frac{\alpha (\Delta t)^\alpha }{2AB(\alpha ) \Gamma (\alpha +3)} \sum _{\mu =2}^{\delta } [ t_{\mu }^{1-\beta } I_1 (t_{\mu }, S^{\mu }, D^{\mu }, E^{\mu }, I^{\mu }, C^{\mu }, R^{\mu })- 2t_{\mu -1}^{1-\beta } I_1 (\mho ) \nonumber \\{} & {} \quad - t_{\mu -2}^{1-\beta } I_1 (\Theta ) ] \times \zeta , \end{aligned}$$
(85)
$$\begin{aligned}{} & {} C^{\delta +1} = \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } C_1 (t_{\delta }, S^{\delta }, D^{^\delta }, E^{\delta }, I^{\delta }, C^{\delta }, R^{\delta })+ \frac{\alpha (\Delta t)^\mu }{AB(\alpha ) \Gamma (\alpha +1)} \nonumber \\{} & {} \quad \sum _{\mu =2}^{\delta } t_{\mu -2}^{1-\beta } C_1 (\Theta ) \times \Psi + \frac{\alpha (\Delta t)^\alpha }{AB(\alpha ) \Gamma (\alpha +2)} \sum _{\mu =2}^{\delta } \Big [ t_{\mu -1}^{1-\beta } C_1 (\mho ) - t_{\mu -2}^{1-\beta } C_1 (\theta ) \Big ] \times \Phi \nonumber \\{} & {} \quad + \frac{\alpha (\Delta t)^\alpha }{2AB(\alpha ) \Gamma (\alpha +3)} \sum _{\mu =2}^{\delta } [ t_{\mu }^{1-\beta } C_1 (t_{\mu }, S^{\mu }, D^{\mu }, E^{\mu }, I^{\mu }, C^{\mu }, R^{\mu })- 2t_{\mu -1}^{1-\beta } C_1 (\mho ) \nonumber \\{} & {} \quad - t_{\mu -2}^{1-\beta } C_1 (\Theta ) ] \times \zeta , \end{aligned}$$
(86)
$$\begin{aligned}{} & {} R^{\delta +1} = \frac{1-\alpha }{AB(\alpha )} t_{\delta }^{1-\beta } R_1 (t_{\delta }, S^{\delta }, D^{^\delta }, E^{\delta }, I^{\delta }, C^{\delta }, R^{\delta })+ \frac{\alpha (\Delta t)^\mu }{AB(\alpha ) \Gamma (\alpha +1)} \nonumber \\{} & {} \quad \sum _{\mu =2}^{\delta } t_{\mu -2}^{1-\beta } R_1 (\Theta ) \times \Psi + \frac{\alpha (\Delta t)^\alpha }{AB(\alpha ) \Gamma (\alpha +2)} \sum _{\mu =2}^{\delta } \Big [ t_{\mu -1}^{1-\beta } R_1 (\mho ) - t_{\mu -2}^{1-\beta } R_1 (\theta ) \Big ] \times \Phi \nonumber \\{} & {} \quad + \frac{\alpha (\Delta t)^\alpha }{2AB(\alpha ) \Gamma (\alpha +3)} \sum _{\mu =2}^{\delta } [ t_{\mu }^{1-\beta } R_1 (t_{\mu }, S^{\mu }, D^{\mu }, E^{\mu }, I^{\mu }, C^{\mu }, R^{\mu })- 2t_{\mu -1}^{1-\beta } R_1 (\mho ) \nonumber \\{} & {} \quad - t_{\mu -2}^{1-\beta } R_1 (\Theta ) ] \times \zeta . \end{aligned}$$
(87)

Where

$$\begin{aligned} \Psi= & {} [(\delta - \nu +1 )^\alpha -(\delta -\nu )^\alpha ]. \end{aligned}$$
(88)
$$\begin{aligned} \Theta= & {} t_{\nu -2}, S^{\nu -2}, D^{\nu -2}, E^{\nu -2}, I^{\nu -2}, C^{\nu -2}, R^{\nu -2}. \end{aligned}$$
(89)
$$\begin{aligned} \mho= & {} t_{\mu -1}, S^{\nu -1}, D^{\nu -1}, E^{\nu -1}, I^{\nu -1}, C^{\nu -1}, R^{\nu -1}. \end{aligned}$$
(90)
$$\begin{aligned} \Phi= & {} \Big [(\delta - \nu +1 )^\alpha (\delta -\nu +3+2\alpha ) - (\delta -\nu )^\alpha (\delta -\nu +3+3\alpha ) \Big ]. \end{aligned}$$
(91)
$$\begin{aligned} \zeta= & {} \Big [(\delta - \nu +1 )^\alpha \Big ( 2(\delta -\nu )^2 + (3\alpha +10)(\delta -\nu ) + 2\alpha ^2 +9\alpha +12 \Big )\nonumber \\{} & {} - (\delta -\nu )^\alpha \Big ( 2(\delta -\nu )^2+ (5\alpha +10)(\delta -\nu ) + 6\alpha ^2 +18\alpha +12 \Big ) \Big ]. \end{aligned}$$
(92)

Findings and results

Here is the numerical simulation of an advanced strategy for representing the coexistence of COVID-19 and diabetes, using a fractal fractional approach. Our approach combines the COVID-19 model with the Diabetes model, incorporating fractal–fractional derivatives with Mittag-Leffler kernels, while considering specific initial conditions. To validate the model, we utilized confirmed case data from the Ghana Health Service for March and September 2020. The parameter values and starting values from a previous study7 were employed. By solving a nonlinear system of fractional differential equations, we obtained simulation results for different fractional orders a, which are depicted in Figs. 1, 2, 3, 4, 5, 6. These figures showcase the COVID-19 model with diabetes, comparing the outcomes of fractal–fractional orders with those obtained using integer order. All trajectories exhibit consistent patterns and are ultimately connected to the true belonging equilibrium site. The trajectories in Figs. 1, 2, 3, 4, 5, 6 correspond to specific values of the fractional order variable a, with respective fractal dimensions of \(\beta =1\) and \(\beta =0.8\). These figures provide insights into the dynamics of the disease among the susceptible population (S), susceptible individuals with diabetes (D), individuals exposed to COVID-19 (E), cases of COVID-19 with diabetes (C), and the recovered population (R). It is apparent that each graph in Fig. 1 has a distinct convergence rate (depending on \(\alpha\)), but they all eventually converge towards the steady state. In Fig. 1, it is evident that increasing the value of \(\alpha\) leads to a decrease in the susceptible population. This trend is consistent across different fractal dimensions, i.e., \(\beta =1\) and \(\beta =0.8\). In Fig. 2, it is observed that an increase in the fractional order variable \(\alpha\) results in a corresponding increase in the susceptible population with diabetes. Similarly class E, I, C and R exhibit an increase with respect to larger fractional order \(\alpha\) as seen in Figs. 3, 4, 5, 6. A susceptible individual without diabetes decreases strictly while the susceptible class with diabetes patient rises strictly and comes to a stable position due to recovered individuals as can be seen in Fig. 1 and 2 respectively. Infected class without diabetes as well as with diabetes patients decreases by decreasing fractional value with the minor effect of dimension due to the same recovery rate as can be seen in Figs. 4 and 5 respectively. The influence of fractional and fractal elements on the dynamics of the model under study is evident. Through simulations of the proposed design, the total density of all compartments, reflecting internal behavior, is observed to vary between 0 and 1. For improvement of results can be observed easily at fractal dimension 0.6 in Figs. 1c,2s,3c,4c,5c and 6c for all commeasurement here is more bounded to steady state point with feasible regions.

The graphical results vividly demonstrate the successful accomplishment of the intended objective. Furthermore, extending the clause will importantly enhance the effectiveness of the procedure. Enhanced precision and dependability of solutions across all sections are achieved by reducing fractional values. The graphical solutions vividly depict the propagation dynamics of the virus, highlighting the influence of diabetes, and showcasing the memory effect attributed. The proposed model offers greater flexibility than conventional derivatives. Fractional order derivations, surpassing classical order in terms of accuracy and reliability, proved to be more effective in elucidating physical processes. These operators hold greater value compared to the existing non-integer order types. The presented numerical conclusions illustrate the behavior of dynamics within the distinct fractal orders, providing valuable insights.

Figure 1
figure 1

S(t) using fractal–fractional operator.

Full size image
Figure 2
figure 2

D(t) using fractal–fractional operator.

Full size image
Figure 3
figure 3

E(t) using fractal–fractional operator.

Full size image
Figure 4
figure 4

I(t) using fractal–fractional operator.

Full size image
Figure 5
figure 5

C(t) using fractal–fractional operator.

Full size image
Figure 6
figure 6

R(t) using fractal–fractional operator.

Full size image

Conclusion

Throughout history, the spread of illnesses has had a disastrous impact on communities, and managing and minimizing this impact has been greatly aided by the numerical pattern. We want to determine the stable position and effectiveness of the suggested strategy by exposing it to both qualitative and quantitative criticisms. To determine how sensitive each parameter is, the sensitivity of every parameter in the suggested system is confirmed. An extended analysis of fractal fractional operators is presented, emphasizing the application of the Mittag-Leffler kernel. To observe the importance of high fractional order conduct, we executed simulations using Matlab. When the fractional contractor is applied to the mathematical modeling of the COVID-19 with diabetes model, it yields remarkably good results. Through simulations, we have managed to clarify the complex interplay between fractal and fractional orders by seeing how changing the fractional order affects the behavior of the suggested model. The proposed model is a helpful tool for simulating COVID-19 dynamics in patients with diabetes, providing information on the course of the disease from the beginning to the end. Fractional operators are useful for analyzing the course of an illness. The numerical simulation’s findings showed that a higher death toll happened in cases when the infected person had diabetes as an underlying condition; as a result, these individuals need special treatment. Policymakers and public health experts can use the validated data to gain important insights that will help them put policies in place to stop the development of COVID-19 among people with diabetes. With time-dependent. control measures, the dynamics of the suggested model can be investigated further by utilizing generalized fractional operators with nonlocal and nonsingular kernels.