Abstract
Hippocampal representations that underlie spatial memory undergo continuous refinement following formation1. Here, to track the spatial tuning of neurons dynamically during offline states, we used a new Bayesian learning approach based on the spike-triggered average decoded position in ensemble recordings from freely moving rats. Measuring these tunings, we found spatial representations within hippocampal sharp-wave ripples that were stable for hours during sleep and were strongly aligned with place fields initially observed during maze exploration. These representations were explained by a combination of factors that included preconfigured structure before maze exposure and representations that emerged during θ-oscillations and awake sharp-wave ripples while on the maze, revealing the contribution of these events in forming ensembles. Strikingly, the ripple representations during sleep predicted the future place fields of neurons during re-exposure to the maze, even when those fields deviated from previous place preferences. By contrast, we observed tunings with poor alignment to maze place fields during sleep and rest before maze exposure and in the later stages of sleep. In sum, the new decoding approach allowed us to infer and characterize the stability and retuning of place fields during offline periods, revealing the rapid emergence of representations following new exploration and the role of sleep in the representational dynamics of the hippocampus.
Similar content being viewed by others
Main
Memories are continuously refined after they form. Different stages of sleep have important roles in the transformations that memories undergo, but many aspects of these offline processes remain unknown. Memories that involve the hippocampus are particularly affected by sleep, which alters molecular signalling, excitability and synaptic connectivity of hippocampal neurons2,3. Memories are considered to be represented by the activity of ensembles of neurons that form during experience4. In the rat hippocampus, these ensembles are tuned to locations in a maze environment5. Indeed, an animal’s position can be decoded from the spike trains recorded from a population of neurons6 (Fig. 1a). Spatial representations, however, do not remain stationary following initial formation. In many cases, the place fields (PFs) of hippocampal neurons develop and shift during traversals of an environment7,8, remap upon exposure to different arenas9 and reset or remap even with repeated exposure to the same place1,10. This presents a challenge to traditional decoding approaches that rely on the assumption that hippocampal neurons always represent the same maze positions as they do in a specific behavioural session11, including mazes that the animal has yet to experience12.
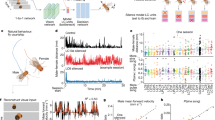
a, Hippocampal place cells show tuning to specific locations (PFs) on a linear track maze. When animals sleep or rest outside the maze, the spiking of these neurons is no longer driven by maze locations, x, but may represent internally generated simulations of x or other locations. b, We used Bayesian learning to assess each neuron’s tuning \({p}^{{\prime} }({\rm{spike}}| x)\) for internally generated cognitive space, x, using the PFs of all other neurons recorded on the maze, under the assumption of conditional independence among Poisson spiking neurons conditioned on space (Methods). Top left: sample spike raster during an example maze traversal. Top right: spiking patterns of the same cells during a brief window in sleep. For each iteration, one cell is selected as the learning neuron. Bottom left: population activity extracted for time bins in which the learning neuron spikes. Bottom middle: next, posterior probability (prob.) distributions are constructed using the spikes and track tunings of the other neurons during these time bins. Max., maximum. Bottom right: the Bayesian LT \({p}^{{\prime} }({\rm{spike}}| x)\) is equal to the summation of the posterior distributions over these time bins (\(\sum p(x| {\rm{spike}})\)), normalized by the overall likelihood of each track location (\(\sum p(x)\)) obtained across the entire offline period. c, Example tunings derived from single ripple events recorded during rest and sleep in the home cage following maze exposure. For each offline ripple event, shown are the spike raster (left) with ripple band signal above, tunings learned for each unit from the raster (middle) and the PFs on the maze (right). Although, in principle, tunings can be derived from individual events, in practice they are best evaluated by combining across multiple ripple events (Extended Data Fig. 1). Scale bars, 50 cm (a) and 1 s (b). Drawings of rats in a by E. Ackermann, reproduced from https://github.com/kemerelab/ratpack/ under a Creative Commons licence CC BY-SA 4.0.
We conjectured that modifications of spatial representations would take place during sleep when connections between some neurons are strengthened while those between other neurons are weakened2,13. Consistent with this conjecture, cells that become active in a new environment continue to reactivate for hours during sharp-wave ripples in sleep14, suggesting that offline processes during sleep involve the spatial representations of hippocampal neurons. Moreover, the collective hippocampal map of space shows changes following sleep15 and some cells express immediate early genes during this period that can mark them for sleep-dependent processing16. However, although spatial representations are readily measured from the spiking activities of neurons when animals explore a maze environment, access to these non-stationary representations is lost when animals cease exploring, making it challenging to evaluate how spatial representations are shaped over time.
To evaluate and track the spatial preferences of a neuron across online and offline periods, we developed a new method based on Bayesian learning17 (Fig. 1b,c). Under the assumption of conditional independence of Poisson spike counts from hippocampal neurons conditioned on location, we derived the Bayesian learned tuning (LT) of a neuron from the spike-triggered average of the posterior probability distribution of position determined from the simultaneous spiking patterns of all other neurons in the recorded ensemble, including for time periods when animals were remote from the maze locations for which position was specified. In this formalism, the internally generated preference of a neuron for a location is revealed through its consistent coactivity with other neurons in the ensemble associated with that position. These Bayesian LTs allowed us to track the place preferences of neurons as they evolved in exceptionally long-duration (up to 14 h) hippocampal unit recordings, enabling us to identify those periods and events in which the firing activities of neurons were consistent or inconsistent with PFs on the maze and to characterize the plastic offline changes in tuning relative to the broader ensemble.
Spatial tunings post maze align with maze PFs
We first examined how tuning curves are affected by an animal’s experience on a maze by characterizing the representations of neurons from spike trains recorded from the rat hippocampus in experiments in which rest and sleep in a home cage both preceded (PRE) and followed (POST) exposure to a new track (MAZE), in which rats ran for water reward. To examine spatial tunings in each brain state separately, we first separated unit and local field potential data recorded from hippocampal region CA1 into different states using general criteria (Methods) for rapid eye movement (REM) sleep (sleep featuring prominent hippocampal θ-oscillations), ripple periods during rest and sleep (150–250 Hz band power accompanied by high multi-unit firing rates), slow-wave sleep (SWS) periods exclusive of ripples and active wake (with prominent θ-oscillations). We calculated PFs and the LTs for each epoch for all pyramidal units with peak spatial firing rates >1 Hz on the maze (Fig. 2a–c). We limited the initial analysis to the first 4 h of POST, during which we expect greater similarity to maze firing patterns14. LTs showed a wide distribution of fidelity to PFs from PRE to POST depending on brain state. Population vector correlations between spatial bins in PFs and LTs (Fig. 2b) and LT–PF Pearson correlation coefficients (Fig. 2c) demonstrated that the highest fidelities to PFs were observed in spatial representations during θ-oscillations and ripples on the maze, as expected18,19,20. However, among offline periods only spatial tunings evidenced during POST, particularly those during ripples, showed significant correlations with unit PFs in MAZE, and notably not those during PRE. LTs that exhibited fidelity to MAZE PFs could be composed from individual ripple events (Fig. 1c) but improved by averaging over multiple events (Extended Data Fig. 1). These differences were not due to differences in the proportion of time in rest versus sleep or in the number of active firing bins (Extended Data Fig. 1c). The fidelity of LTs further varied during SWS; tunings derived from ripples during periods of high δ-oscillation (0.5–4 Hz) and high spindle (8–16 Hz) power exhibited higher PF fidelities compared to those from periods with low power (Extended Data Fig. 2a–c). Notably, we observed weak but significantly aligned representations consistent with the maze during POST REM sleep, when vivid dream episodes are frequently experienced21. These representations were best aligned at the trough and descending phase of REM θ-oscillations (Extended Data Fig. 2f), which may reflect that only specific time windows during REM sleep correspond to previous experience22. Overall, these findings provide a measurement of the temporal variations in hippocampal ensemble firing patterns and indicate that neurons maintain internal tunings consistent with their PFs on the maze primarily during ripples in POST SWS.
a, PFs of hippocampal units pooled across sessions (n = 660 units from 15 sessions and 11 rats) alongside Bayesian LTs calculated separately for each behavioural epoch (PRE, MAZE and POST) and brain state (ripples in SWS and quiet wake (QW), non-ripple SWS, REM and active home cage). Blanks reflect instances without neuronal firing for the specified state and epoch (for example, no REM activity in PRE). Only tunings learned on the MAZE and POST bear a visual resemblance to PFs, particularly those during ripples. b, The LT–PF correlations of the population vectors (PVs) across space calculated between PFs and each set of LTs in a. c, Cumulative distributions of PF fidelity for each set of LTs in a, defined as Pearson correlation coefficients between the LTs and PFs (LT–PF fidelity), compared to null distributions obtained from unit-identity shuffles (grey, but occluded in many instances). Individual session medians (dots) and corresponding interquartile range (horizontal lines) are overlaid and colour-coded by dataset (Grosmark, Giri, and Miyawaki). Only tunings learned on the MAZE and POST exhibited significant median fidelities compared (one-sided) to null distributions obtained from 104 unit-identity shuffles (PRE: SWS ripples P = 0.24, quiet wake ripples P = 0.93, non-ripple SWS P = 0.17, REM P = 0.53, active home cage P = 0.21; MAZE: θ-oscillations P < 10−4, quiet wake ripples P < 10−4; POST: SWS ripples P < 10−4, quiet wake ripples P < 10−4, non-ripple SWS P = 0.04, REM P = 0.02, active home cage P = 0.12; see also Extended Data Fig. 2). *P < 0.05, ***P < 0.001.
Spatial representations are more stable post maze
We next tracked the LTs of neurons over time and examined the consistency of their place preferences in different epochs. We calculated LTs from all ripple events in 15-min windows sliding in 5-min steps during each session, from PRE through MAZE and the first 4 h of POST. Sample unit tunings from a recording session are shown in Fig. 3a (additional examples are provided in Extended Data Fig. 3). These examples show stable LTs for successive time windows during POST, and in some instances also during PRE. To quantify the overall stability of LTs for each unit, we used Pearson correlation coefficients to assess the consistency of the LTs across time windows within and between behavioural epochs (Fig. 3b). High off-diagonal values in the correlation matrices within an epoch indicated that the LT remained stable during that epoch. For the example units in Fig. 3a, we compared the median LT stability values from each epoch against shuffle distributions generated by randomizing the unit identities of the LTs at each time window (Fig. 3c). This z-scored LT stability was >0 in both PRE and POST in this session (Fig. 3d) and for data pooled across all sessions (Fig. 3e), but it was significantly higher in POST compared to PRE, revealing that POST sleep representations were more stable than those in PRE. When we measured the LT stability across time windows from PRE and POST epochs, to examine their consistency from before to after the new maze exposure when PFs first form, the PRE with POST LT stability was not significantly greater than 0 in the example session (median = 0.65, P = 0.16), rose to significance in the pooled data (P < 10−4, Wilcoxon signed rank test (WSRT, n = 660)), but remained significantly lower than the stabilities observed within PRE and POST (PRE versus PRE with POST: P < 10−4; POST versus PRE with POST: P < 10−4, WSRT (n = 660)), thus signalling that only a small minority of units maintained the same consistent spatial tuning from before to after maze exposure.
a, Heat maps of LTs exclusively during ripples for sample units in sliding 15-min windows (hypnogram on top left indicates quiet wake, active wake (AW), REM sleep and SWS states) from PRE to POST (maze PFs in grey, vertical on right) show stable LTs during POST. Units 5 and 6 show stable tunings during PRE ripples that do not align with their maze PFs. b, The matrix of LT correlation coefficients across time for units in a. c, Stability of the LTs (black) for units in a, defined as the median of the correlation coefficient between LTs from non-overlapping 15-min windows. Violin plots (grey) show chance distributions obtained from non-identical units randomly scrambled across windows (1,000×). Although LTs of units 5 and 6 were stable in PRE and POST, they were not consistent across these epochs. d,e, Unit LT stabilities z-scored against unit-identity shuffles were significantly greater than 0 for the sample session (PRE: median = 2.51, P = 3.9 × 10−9; POST: median = 13.78, P = 2.8 × 10−14; PRE with POST: median = 0.65, P = 0.16; two-sided WSRT (n = 77)) with individual units shown as dots (d), and all sessions pooled together (PRE: median = 2.47, P = 4.4 × 10−67; POST: median = 3.10, P = 4.6 × 10−79; PRE with POST: median = 0.95, P = 1.1 × 10−13; two-sided WSRT (n = 660); e). Overall, LT stability was higher in POST than in PRE (P = 0.02) or between PRE with POST (P ≤ 1.9 × 10−70; two-sided WSRT (n = 660)). Median values from individual sessions overlaid and colour-coded by dataset. f, Distributions of PF fidelity (r(LT, PF)) for units with stable (z > 2) versus unstable (z < 2) LTs showed no difference in PRE (P = 0.29) but were higher for stable units in POST (P = 2.1 × 10−11; two-sided Mann–Whitney U-test (n = 660)). NS, not significant; *P < 0.05; ***P < 0.001.
A subset of units showed remarkably stable LTs during PRE, which compelled us to consider whether the LTs of those units might show higher fidelity with maze PFs. To test this conjecture, we divided units into ‘stable’ and ‘unstable’ on the basis of whether their z-scored LT stability was greater or less than 2 (PRE: 371 stable versus 289 unstable; POST: 454 stable versus 206 unstable), respectively, in both PRE and POST (Fig. 3f). In POST, units with both stable and unstable LTs showed significant PF fidelity (P < 10−4, comparison against 104 unit-identity shuffles). However, the PF fidelity of units with stable LTs was significantly higher compared to that of units with unstable LTs in POST. By contrast, in PRE there was no significant difference between PF fidelities of stable and unstable units, and neither of these subsets showed significantly greater PF fidelity compared to a surrogate distribution obtained by shuffling unit identities (PRE stable LTs: P = 0.06; PRE unstable LTs: P = 0.35; POST stable LTs: P < 1 × 10−4; POST unstable LTs: P = 2 × 10−4). Next we tested whether the subset of ripple events in PRE that featured high replay scores (Extended Data Fig. 4 and Supplementary Information) might show better PF fidelity. Even so, we found little alignment between maze PFs and LTs constructed from these events. These findings demonstrate that although some units in PRE exhibit stable learned spatial tunings, these tunings do not typically anticipate their future PFs, but rather show a broad distribution of alignments with the maze place preferences. By contrast, LTs constructed from low-replay-score events from POST showed strong fidelity to maze PFs, despite the absence of sequential trajectories in low-score events (Supplementary Information and Extended Data Fig. 4). Thus, events that would typically be classified as non-replays in POST maintain representations that are faithful to the maze PFs.
Although the stability and fidelity of spatial tunings were significantly greater in POST, these features did not last indefinitely. In our data that involved several hours of POST, we observed decreases in both the fidelity and stability of Bayesian LTs over the course of sleep (Fig. 4). The similarity of sleep representations to maze PFs decreased progressively over POST, eventually reaching levels similar to those in PRE. The stability of spatial tunings also decreased over this period, indicating that at the ensemble level these representations become less coherent in later periods of sleep. The dissolution of representational alignment with the maze over the course of sleep may reflect an additional important aspect of sleep, distinct from that of reactivation and replay23,24.
a, Heat maps of ripple LTs for sample units in sliding 15-min windows throughout a sample long-duration session show gradual decreases in LT stability over time. A matrix of correlation coefficients between LTs from different time windows is provided on the right for each unit. b, PF fidelity (correlation coefficient between LTs and PFs) shows a gradual decrease over time in POST. The colour traces show median values across units in each session. The black trace and grey shade depict the median and interquartile range of the pooled data. PRE and MAZE epochs of differing durations were aligned to the onset of MAZE, and POST epochs were aligned to the end of MAZE. c, Top panels: LT stability correlation matrices averaged over all recorded units, shown separately for each dataset. Here, the matrix for each unit was z-scored against unit-identity shuffles before averaging. Bottom panels: the distribution of z-scored LT stability in overlapping 2-h blocks during POST, separately for each dataset. Comparisons across consecutive blocks were carried out using two-sided Mann–Whitney U-tests with no correction for multiple comparisons (Grosmark dataset: P < 10−4, P = 0.75, P < 10−4; Giri dataset: P = 0.81, P < 10−4, P < 10−4, P < 10−4, P = 0.04, P = 0.08, P = 0.77, P = 0.005; Miyawaki dataset; P = 0.47, P = 2 × 10−4). NS, not significant; *P < 0.05; ***P < 0.001.
Stability and retuning during sharp-wave ripples
Recent studies report that PFs drift and frequently remap with repeat exposures to the same environment1,10,15,25,26,27 although it is unclear when and how these representational changes emerge. Given that the tunings learned during POST ripples exhibit a diversity of PF fidelities, some aligned but others misaligned with maze PFs, we investigated whether these representations relate to the future spatial tunings of the cells. In three recording sessions from two animals, we re-exposed rats back to the maze environment after about 9 h of POST rest and sleep (Fig. 5a). We labelled these epochs ‘reMAZE’ and compared the PFs across maze exposures with the ripple LTs from the intervening POST period (Fig. 5b–d). POST ripple LTs showed significant correlations with PFs from both maze exposures, indicating a continuity of representations across these periods. However, PFs were not identical between MAZE and reMAZE (Fig. 5b), illustrating that neuronal representations drift and remap in the rat hippocampus1 (see also Extended Data Fig. 5). Consistent with our hypothesis that representational remapping in POST could account for PF deviations across repeated maze exposures, in instances in which we saw reMAZE PFs congruent with MAZE PFs (Fig. 5e, top), the POST LTs for those cells showed strong fidelity with the maze period. Yet, in instances in which reMAZE PFs deviated from the MAZE PFs (Fig. 5e, bottom, and time-evolved examples in Fig. 5h and Extended Data Fig. 6), the POST LTs for those units predicted the PFs observed during maze re-exposure. Likewise, we observed a significant correlation between PF fidelities in POST and the reMAZE–MAZE similarity (Fig. 5f). These correlations were significant for cells with both weak and strong PF stability on the MAZE (Extended Data Fig. 5e,f) and were stronger for tunings learned from SWS than from quiet wake (Extended Data Fig. 5g,h). To better examine whether ripple representations during POST can presage representational changes across maze exposures, we carried out a multiple regression analysis to test the extent to which reMAZE PFs are explained by MAZE PFs and LTs from PRE or POST (first 4 h). We also included the average LTs (over PRE and POST) to control for the general deviations of LTs that were not specific to any unit, as well as ‘latePOST’ LTs constructed from the last 4 h of POST before reMAZE (Fig. 5g). This regression demonstrated a significant contribution (β-coefficient) for MAZE PFs, as expected, indicating that there is significant continuity in PFs across maze exposures. However, it also revealed that POST LTs, but not PRE LTs, affect the PF locations in maze re-exposure. Remarkably, we found no significant contribution from the latePOST LTs, indicating that our observations do not simply arise from temporal proximity between POST sleep and the maze re-exposure, or from general dissolution and instability of LTs in time (see also Extended Data Fig. 5i), but rather reflect rapid changes in representations that are manifested in the initial hours of sleep. Inspection of individual LTs (Fig. 5h; see also Extended Data Fig. 6) showed multiple instances in which LTs from early POST periods showed spatial preferences that shifted away from MAZE PFs but were better aligned with their future reMAZE tunings. Overall, these results demonstrate the critical role of POST sleep in stabilizing and reconfiguring the spatial representations of hippocampal neurons across exposures to an environment.
a, Timeline for sessions (n = 3) in which the animal was re-exposed to the same maze track (reMAZE) after >9 h from initial exposure (MAZE). We used the first 4 h of POST to calculate LTs. ZT, zeitgeber time. b, Cumulative distribution of PF similarity between MAZE and reMAZE, compared (one-sided) to null distributions obtained from unit-identity shuffles (grey; P < 10−4). c, Cumulative distribution of POST PF fidelity (correlation coefficient between POST LTs and MAZE PFs; P < 10−4). d, Cumulative distribution of correlation coefficient between POST LTs and reMAZE PFs (P < 10−4). In b–d, P values were obtained by comparing the median (one-sided) against those from surrogate distributions from 104 unit-identity shuffles. e, Example units with high MAZE–reMAZE similarity and high POST PF fidelity (top row), or low MAZE–reMAZE similarity and low POST PF fidelity (bottom row). The rightmost column shows the degree of similarity between the reMAZE PFs and POST LTs for each unit. f, MAZE–reMAZE similarity correlated with POST PF fidelity. The best linear fit and 95% confidence intervals are overlaid with a black line and shaded grey, respectively. g, Multiple regression analysis for modelling reMAZE PFs using PRE LTs, MAZE PFs, POST LTs and latePOST LTs (beyond first 4 h) as regressors (R2 = 0.19, P < 10−4, c0 = 0, c1 = 0.13, β1 = −0.02, P = 0.77, β2 = 0.31, P < 10−4, β3 = 0.14, P < 10−4, β4 = −0.01, P = 0.58; P values were obtained by comparing the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of reMAZE PFs). The overlaid circular markers depict regression coefficients obtained by leaving out one session at a time. h, Heat maps of ripple LTs for sample units in sliding 15-min windows from different sessions (session hypnograms on top, as in Fig. 3; MAZE and reMAZE PFs and LTs during PRE, POST and latePOST on the right). Note the rapid emergence of LTs during POST that showed alignment with their future PFs during reMAZE. ***P <0.001. Drawings of rats in a by E. Ackermann, reproduced from https://github.com/kemerelab/ratpack/ under a Creative Commons licence CC BY-SA 4.0.
Awake ripples and θ-oscillations direct post-maze tunings
Our findings thus far indicate that the neuronal firing patterns during POST ripples reflect both stable and retuned PF representations following the maze. We next investigated the factors that conspire to establish these patterns. Two recent studies28,29 indicate that, more so than PF activity, the spike patterns of neurons during waking θ-oscillations provide the necessary conditions for establishing the firing patterns observed during POST sleep. Other studies, however, suggest that awake ripples are a primary mechanistic candidate for generating stable representations30,31. Adding further complication, several studies have indicated that PRE and POST ripples share overlapping activity structure14,32,33, suggesting limits on the flexibility of sleep representations. To better understand the respective contributions of these different factors on the representations in POST sleep, we carried out a multiple regression to test the extent to which POST LTs are explained by PRE LTs, MAZE PFs, LTs of MAZE θ-oscillation periods and LTs of MAZE ripples (Fig. 6a). Remarkably, we found that the β-coefficients for all of these regressors were significant. The β-coefficient for MAZE θ-oscillation LTs was significant, indicating that waking θ-oscillations, particularly at the trough of θ-waves (Extended Data Fig. 7e,f), are important for the formation of ensemble representations28,29. Consistent with this, the stability of PFs on the MAZE was significantly predictive of the stability and fidelity of LTs during POST (Extended Data Figs. 7 and 8). However, overall, MAZE ripple LTs had the largest β-coefficient, indicating that firing patterns during wake ripples on the maze have the most lasting impact on POST ripple activity30,31. Remarkably, the second largest β-coefficients were observed for PRE ripple LTs, indicating that next to MAZE patterns, patterns configured in PRE also provide an important determinant of POST sleep activity32,33,34. Consistent with this, we observed a significant correlation between the PF fidelity in PRE and the PF fidelity in POST (Fig. 6b).
a, Multiple regression analysis for estimating the dependence of POST LTs on PRE LTs, MAZE PFs, MAZE θ-oscillation LTs and MAZE ripple LTs shows that POST LTs were most significantly affected by PRE LTs and MAZE ripple LTs (R2 = 0.51, P < 10−4, c0 = 0, c1 = 0.18, β1 = 0.29, P < 10−4, β2 = 0.06, P < 10−4, β3 = 0.13, P < 10−4, β4 = 0.32, P < 10−4; P values were obtained by comparing (one-sided) the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of POST LTs). The overlaid circles mark regression coefficients obtained by leaving out one session at a time. b, PF fidelity (correlation with MAZE PF) was significantly correlated between PRE and POST LTs. In b–f, the best linear fits and 95% confidence intervals are overlaid with a black line and shaded grey, respectively. c, Sleep similarity (correlation coefficient between PRE and POST LTs) was correlated with PRE PF fidelity, indicating that high-fidelity PRE LTs are preserved in POST. d, An overall negative correlation between sleep similarity and POST PF fidelity. e, When we split units into relatively PRE-tuned (PRE PF fidelity > median of shuffle distribution) and PRE-untuned units (PRE PF fidelity < median of shuffle distribution), sleep similarity (top histogram) and POST fidelity (right histogram) were both high for PRE-tuned cells, with a positive correlation (R2 = 0.50, P = 0.0004) for the subset of cells that were significantly PRE-tuned (white circles, 46 out of all 660 units). f, For PRE-untuned cells, a negative correlation between POST PF fidelity and sleep similarity indicates a continuum of flexible retuning to maze PF. ***P < 0.001.
These observations suggest that despite the absence of maze tuning in PRE sleep, some cells maintain similar representations between PRE and POST. Sleep similarity, which measures the consistency of LTs across PRE and POST by assessing the correlation between PRE LTs and POST LTs, was significantly correlated with PF fidelity in PRE (Fig. 6c); thus, PRE LTs that aligned with maze PFs, presumably by chance, maintained those LTs in POST (see also individual examples in Extended Data Fig. 3, such as in rat N). By contrast, sleep similarity showed a weak negative correlation with the PF fidelity in POST (Fig. 6d), consistent with the notion that these measures respectively reflect neuronal rigidity and flexibility. To better understand the difference between PRE and POST LTs, we separated units into relatively ‘PRE-tuned’ (PRE PF fidelity > median of shuffles) and ‘PRE-untuned’ (PRE PF fidelity < median of shuffles) cells. PRE-tuned cells showed generally high POST PF fidelity along with high sleep similarity (Fig. 6e), with a positive correlation in these variables in the further subset of cells that were significantly PRE-tuned cells relative to unit-identity shuffles. By contrast, PRE-untuned cells showed a significant negative correlation between sleep similarity and POST fidelity (Fig. 6f); those with high sleep similarity were poorly tuned in POST, whereas those that reconfigured from PRE to POST showed better fidelity to maze PFs. These analyses therefore reveal the contribution of PRE sleep to maze representations and POST activities; cells whose representations are already aligned with maze PFs in PRE maintain those same representations in POST, but other neurons exhibit a broad range of flexible reconfiguration that is inversely proportional to their rigidity34 across PRE and POST.
Discussion
The observations of dynamic representations in offline states made possible by Bayesian learning have important implications for our understanding of how learning and sleep affect the PF representations of hippocampal neurons. First, we found that neural patterns occurring in PRE reconfigure during exposure to a new environment. Although ripple events during pre-exposure occasionally scored highly for replays, spatial representations were not coherent among active neurons during these periods, as cells with very divergent PFs often fire within the same time bins (for example, Extended Data Fig. 4d,e). These observations suggest that continuous patterns in the decoded posteriors of spike trains could emerge spuriously. Consistent with this notion, it has been noted that the measures and shuffles used to quantify replays inevitably introduce unsupported assumptions about the nature of spontaneous activity11,33,35,36. We propose that only for those periods and events in which there is strong correspondence between Bayesian LTs and neurons’ PFs, can it be considered valid to apply Bayesian decoding to offline spike trains11.
Among the brain states we examined, sharp-wave ripples in early sleep offered the representations that best aligned with the PFs on the maze. These early-sleep representations emerged from a confluence of factors, including carryover of firing patterns from pre-maze sleep (in both relatively PRE-tuned and PRE-untuned units)33. Most notably, however, our analysis revealed a key role in awake activity patterns during θ-oscillations, particularly at the trough of θ-waves, which corresponds to the encoding phase37,38 (whereas the peak of θ-waves corresponds to greater dispersion and prospective exploration39,40), and more prominently, those during sharp-wave ripples, in generating the ensemble coordination that underlies spatial representations during sleep. This may indicate a greater similarity in co-firing across awake and sleep ripples, compared to that for awake θ-oscillations18 and sleep ripples, although we note that θ-oscillation and ripple LTs both provide strong PF fidelity (Fig. 2). These observations are consistent with the hypothesis that an initial cognitive map of space is first laid down during θ-oscillations19,28,29,41, and then stabilized and continuously updated by replays during awake ripples based on the animal’s (rewarded and/or aversive) experiences on the maze30,31,42,43,44. Once ensembles are established, they reactivate during the early part of sleep14,45. However, sleep representations were not always mirror images of the maze PFs, and our Bayesian learning approach allowed us to measure those deviations for individual neurons. Remarkably, we found that these early-sleep ripple representations proved predictive of PFs on re-exposure to the maze. On the basis of these observations, we propose that representational drift in fact arises rapidly from retuning that takes place during early-sleep sharp-wave ripples rather than noisy deviations that develop spontaneously over time. This could reflect the possibility that single-trial plasticity rules that give rise to new PFs46,47,48 are also at work when animals go to sleep. Furthermore, we conjecture that hippocampal reactivation during sleep does not have a passive role in simply recapitulating the patterns already seen during learning, but represents a key optimization process generating and integrating new spatial tunings with recently formed spatial maps.
Overall, representations remained stable and consistent with the maze for hours of sleep in POST, despite the absence of strong sequential replay trajectories during ripples in POST sleep. Reconciling observations based on studies that measure neuronal reactivation using pairwise or ensemble measures with those that focus on trajectory replays has until now represented a challenge to the field49. Our study consolidates these views by demonstrating that faithful representations, which are consistent with pairwise and ensemble measures of reactivation, persist for hour-long durations. However, the trajectories produced by these cell ensembles do not necessarily provide continuous high-momentum sweeps through the maze environment50,51, as we found high-fidelity spatial tunings even among low-replay-score ripple events in post-maze sleep. Instead, trajectories simulated by the hippocampus during sleep ripples may explore pathways that were not directly experienced during waking but can serve to better consolidate a cognitive map of space42,52. Additionally, we found increasing instability and drift in the spatial representations of neurons over the course of sleep, indicating that late sleep, like PRE, features more randomized activity patterns23,53. It is also worth noting that we found weak alignment between maze PFs and learned spatial tunings during REM sleep, but that this alignment was best at the trough of θ-waves54,55. It may be that under a different behavioural paradigm such as with frequently repeated maze exposures56 or salient fear memories57, we might have uncovered tunings more generally consistent with dream-like replays of maze PFs58. Nevertheless, it is also worth noting that most dreams do not simply reprise awake experiences22. The randomization of representations, as we see during the bulk of REM and late stages of SWS, may reflect an important function of sleep, driving activity patterns from highly correlated ensembles to those with greater independence23,24,59, which may be important for resetting the brain in preparation for new experiences13.
In sum, the Bayesian learning approach provides a powerful means of tracking the stability and plasticity of representational tuning curves of neurons over time, which provides insights into how ensemble patterns form and reconfigure during offline states. Provided a sufficient number of units are sampled (Extended Data Fig. 1), a similar approach can be readily extended to investigate the dynamics of internally generated representations in other neural systems during both sleep and awake states, including in rehearsal, rumination or episodic simulation52,60.
Methods
Behavioural task and data acquisition
We trained four water-deprived rats to alternate between two water wells in a home box to which they had previously been habituated. Owing to the large number of recorded units obtained from each animal, such sample sizes were chosen as typical for demonstrating consistency among subjects. The selections of animals and recorded hippocampal units were essentially random, and analyses and data collection were performed by different personnel. The custom analyses and sequential design prevented investigators from remaining blind to the group allocations. Water rewards during the alternation were delivered through water pumps interfaced with custom-built Arduino hardware. After the animals learned the alternation task, they were surgically implanted under deep isoflurane anaesthesia with 128-channel silicon probes (eight shanks, Diagnostic Biochips) either unilaterally (one rat) or bilaterally (three rats) over the dorsal hippocampal CA1 subregions (anterior–posterior: −3.36 mm, medial–lateral: ±2.2 mm). Following recovery of the rats from surgery, the probes were gradually lowered over a week to the CA1 pyramidal layer, which was identified by sharp-wave-ripple polarity reversals and frequent neuronal firing. After recording stability was ensured, the animals were exposed to new linear tracks during one (three rats) or two (one rat) behavioural sessions (in total five sessions from the four rats). During each session, the implanted animal was first placed in the home box (PRE, about 3 h) with ad libitum sleep (during the dark cycle). Then the animal was transferred to a new linear track with two water wells that were mounted on platforms at either end of the track (MAZE, about 1 h). After running on the linear track for multiple laps for water rewards, the animal was returned to the home box (aligned with the start of the light cycle) for another ≈10 h of ad libitum sleep (POST). In four of these sessions, following POST the rats were re-exposed to the same linear track for another ≈1 h of running for reward (reMAZE).
Wideband extracellular signals were recorded at 30 kHz using an Open Ephys board61 or an Intan RHD recording controller during each session. The wideband activity was high-pass-filtered with a cutoff frequency of 500 Hz and thresholded at five standard deviations above the mean to extract putative spikes. The extracted spikes were first sorted automatically using SpykingCircus62, followed by a manual pass-through using Phy63 (https://github.com/cortex-lab/phy/). Only units with less than 1% of the total number of spikes in their refractory period (on the basis of the units’ autocorrelograms) were included in further analysis. Putative neurons were classified into pyramidal and interneurons on the basis of peak waveform shape, firing rate and interspike intervals64,65. For analysis of local field potentials (LFPs, 0.5–600 Hz), signals were filtered and downsampled to 1,250 Hz.
The animal’s position was tracked using an Optitrack infrared camera system (NaturalPoint) with infrared-reflective markers mounted on a plastic rigid body that was secured to the recording headstage. Three-dimensional position data were extracted online using the Motive software (version 2.1.1), sampled at either 60 Hz or 120 Hz, and later interpolated for aligning with the Ephys data. Although we attempted to track the animal’s position during each entire session, including in the home cage, the cage limited visual access from our fixed cameras. Additionally, in one session the position data for reMAZE was lost during the recording. All animal procedures followed protocols approved by the Institutional Animal Care and Use Committees at the University of Michigan and conformed to guidelines established by the United States National Institutes of Health.
These data constituted the Giri dataset used in our study. We also took advantage of previously published data described in detail in a previous report14. These data consisted of recordings of unit activity and LFPs from the rat hippocampus CA1 region carried out using Cheetah software (version 5.6.0) on a Neuralynx DigitalLynx SX data-acquisition system, with PRE rest and sleep, exposure to a new MAZE, and POST rest and sleep: the Miyawaki dataset (three rats, five sessions; PRE, MAZE, POST, each about 3 h)14,23 and the Grosmark dataset (four rats, five sessions; PRE, and POST, each about 4 h and MAZE, about 45 min)34,66. Vectorized rat images used in the manuscript were provided by E. Ackermann (https://github.com/kemerelab/ratpack/).
Units
In all of these data, we quantified the stability of units across sleep epochs; PRE and POST in Miyawaki and Grosmark sessions, and PRE, POST and latePOST in the Giri dataset (Extended Data Fig. 8). Consistency in isolation distance and firing rate over the sleep epochs were used as stability measures23. Units with isolation distance >15 and firing rate that remained above 33% of the overall session mean during all epochs were considered stable. For all of the analyses in the paper, we required stability during PRE and POST, but for reMAZE prediction analyses (Fig. 5 and Extended Data Fig. 5), we required stability across PRE, POST and latePOST. See Supplementary Tables 1–3 for further details of each session. These data are available upon request from the corresponding author.
PF calculations
To calculate PFs, we first linearized the position by projecting each two-dimensional track position onto a line that best fitted the average trajectories taken by the animal over all traversals within each session. The entire span of the linearized position was divided into 2-cm position bins and the spatial tuning curve of each unit was calculated as occupancy-normalized spike counts across the linearized position bins. We considered only pyramidal units with MAZE PF peak firing rate > 1 Hz for further analyses, except for those in Fig. 5h and Extended Data Fig. 3, in which all stable pyramidal units were included.
PF stability
In each session, the MAZE epoch was divided into six blocks with matching number of laps and then the PFs were separately calculated for each block. Each unit’s PF stability was defined as the median correlation coefficient of PFs across every pair of blocks.
Spatial information
The spatial information67 was calculated as the information content (in bits) that each unit’s firing provides regarding the animal’s location:
in which \({R}_{i}\) is the unit’s firing rate in position bin i, R is the unit’s overall mean firing rate, and Pi is the probability of occupancy of bin i.
LFP analysis and brain state detection
We estimated a broadband slow-wave metric using the irregular-resampling auto-spectral analysis approach68, following code shared by D. Levenstein and the Buzsaki Lab (https://github.com/buzsakilab/buzcode). This procedure allows calculation of the slope of the power spectrum that was used to detect slow-wave activity. The slow-wave metric for each session followed a bimodal distribution with a dip that provided a threshold to distinguish SWS from other periods. A time–frequency map of the LFP was also calculated in sliding 1-s windows, step size of 0.25 s, using the Chronux toolbox (version 2.12)69. To identify high θ-oscillation periods, such as during active wake or REM sleep23,70, the θ-oscillation/non-θ-oscillation ratio was estimated at each time point as the ratio of power in θ-oscillations (4–9 Hz in home cage and 6–11 Hz on the linear track, as we typically observe a small shift in θ-oscillations between these periods70) to a summation of power in the δ-oscillation frequency band (1–4 Hz) and the frequency gap between the first and second harmonics of θ-oscillations (10–12 Hz during home cage awake and REM epochs and 11–15 Hz during MAZE). To calculate the ripple power, multichannel LFP signals were filtered in the range of 150–250 Hz. The envelope of the ripple LFP was calculated using the Hilbert transform, z-scored and averaged across the channels. Only channels with the highest ripple power from each electrode shank were used in the averaging.
Detection of ripple events
For each recording session, multi-unit firing rates (MUA) were calculated by binning the spikes across all recorded single units and multi-units in 1-ms time bins. Smoothed MUA was obtained by convolving the MUA with a Gaussian kernel with σ = 10 ms and z-scoring against the distribution of firing rates over the entire session. Ripple events were first marked by increased MUA that crossed 2z and the boundaries were then extended to the nearest zero-crossing time points on each side. The ripple events that satisfied the following criteria were considered for further analysis: duration between 40 and 600 ms; occurrence during SWS with a θ-oscillation/δ-oscillation ratio < 1 and ripple power > 1.s.d. or during quiet wake with ripple power > 3 s.d. of the mean; and concurrent speed of the animal below 10 cm s−1 (when available). All ripple events were subsequently divided into 20-ms time bins. The onsets and offsets of the events were adjusted to the first time bins with at least two pyramidal units firing. We split ripples with silent periods >40 ms into two or more events. Histograms of ripple durations are reported in Extended Data Fig. 2d.
Bayesian LTs
Consider the following. We recorded from a set of n independent neurons during a maze session and parametrized their spatial tuning curves \({f}_{1}(x)\ldots {f}_{n}(x)\) for positions x on the maze. However, subsequent to the session, we lose the tuning curve for one of the neurons, neuron i. Alternatively, maybe this neuron was inaccessible during the maze session, because of faulty electronics, but we regain access to it in sleep after the maze. We consider whether there is any way that we can learn the tuning curve \(p({{\rm{spikes}}}_{i}| x)\) of neuron i, using information gleaned from firing activity of the other neurons over some period of time T.
Although this may initially seem impossible, if the neurons are all indeed conditionally dependent on position x, and if some internal estimate, thought or imagination of x continues to drive the spiking activity of these neurons, then with enough observation it should be possible to extract the tuning curve through Bayesian learning. Intuitively, if neuron i, has a preference for some position x, then whenever the animal is thinking of x, even if it is no longer on the maze, the neuron i should fire alongside all of the other neurons that have a similar preference for x. However, if neuron i fires randomly with different neurons, then it cannot be said to have any particular spatial tuning for x.
In this paper, we are concerned with estimating tuning curves on the basis of internal representations of position, rather than an external marker. Our motivating hypothesis is that during the periods of estimation, even though some neurons may change their tuning functions, if the ensemble largely maintains its internal consistency then it is informative to measure the tuning curves of individual neurons during these periods. Bayesian decoding has been often used to analyse the position information encoded by the ensemble during offline periods. However, it relies on the assumption that the position preference of neurons does not change over time and experience, which is known to be false for hippocampal neurons.
We model hippocampal neurons as conditionally independent Poisson random variables with firing rates that vary over discretized spatial bins. When an animal explores the maze the firing rate parameters (that is, tuning curves) of observed neurons, \({f}_{\forall j\ne i}(x)\), are typically calculated using the occupancy-normalized spike-triggered average position:
in which the indicator function \({\mathbb{1}}\)\((x={x}_{k})=1\) during periods in which the animal is in position bin \({x}_{k}\) and \({\mathbb{1}}(x\ne {x}_{k})=0\) otherwise. In this work, we also account for directional tuning curves, as discussed below. We define the LT curve for neuron i as \(g\left(x={x}_{k}\right)\), which is the rate parameter of the distribution \(p\left({s}_{i}| x={x}_{k}\right)\), for which we may have some prior beliefs \({p}_{g(x)}\).
The likelihood of the observed data during the LT period can be described as
in which we have taken the tuning curves of the other neurons as known parameters. Using the Bayes rule, we can directly formulate the likelihood of \(g(x)\) from this equation, and then calculate a maximum-likelihood estimate. Note that because the position is considered unobserved during our period of interest, it does not enter into this equation. However, we can introduce it:
in which, in the last line, we have taken advantage of the independence of the position and the activity of the other neurons on the parameters. In Bayesian estimation, the prior, \({p}_{g\left(x\right)}\), allows for the integration of other information into the estimate. For example, we could assume a bias towards a previous measurement that is refined over time or choose a prior such that the shape of g(x) reflects general previous observations of the tuning curves of neurons during behaviour, or more generally one that enforces smoothness over position71. In this work, we assume a general uninformative prior. In such a case, it can be shown (see the section entitled Bayesian LT with uninformative prior) that the maximizing values for the tuning curve are:
Examining this equation, we see that it is quite similar to the normal occupancy-normalized tuning curve estimate, except that we now have the posterior distribution of x rather than binarized counts of occupancy. Moreover, note that this is not actually a closed-form solution, as the parameters appear on both sides of the equality. To avoid an iterative solution, we approximate \(p({x}^{t}={x}_{k}| {s}_{i},{{s}_{\forall j\ne i}}^{t},g(x))\approx p({x}^{t}={x}_{k}| {{s}_{\forall j\ne i}}^{t})\), which is sensible in the case of large numbers of neurons, as the position dependency on any single neuron is small. Thus, we arrive at our estimator for the LT of neuron i.
Finally, note that the denominator here represents the estimated average occupancy during the period in which we are calculating LTs. For the illustrations and analyses in which LTs are evolved over very short time windows (for example, for 15-min sliding windows in Fig. 4 and elsewhere, defined as \(t\in \mathop{T}\limits^{ \sim }\)), we used the estimated average occupancy over the entirety of such periods in the recording (for example, ripples over all of POST in Fig. 4) in the denominator. Thus, for these short windows:
For the tuning curves of the observed neurons, as most of the sessions (16 out of 17) consisted of two running directions on the track, we first calculated the posterior joint probability of position and travel direction and then marginalized the joint probability distribution over travel direction72:
in which \(d\) signifies the travel direction. With the assumption of independent Poisson-distributed firings of individual units conditioned on maze position and direction6,72, we have:
In equation (9), \({f}_{j}(x,d)\) characterizes the mean firing rate of unit \(j\) at position bin \(x\) and direction \(d\) and \(\tau \) is the bin duration used for decoding, which was chosen to be 20 ms in our analyses. By marginalizing the left-hand side of equation (9) over direction \(d\), we obtain
which we have used above to calculate \(p({x}^{t}={x}_{k}| {{s}_{\forall j\ne i}}^{t})\) in each time bin.
We note that though this approach relies on the PFs of neurons measured on the maze to calculate the posterior probability of x, a given neuron’s LT does not depend on its own PF but is learned on the basis of the coherence of its firing with the other neurons in the ensemble. A neuron that fires mostly randomly with other neurons in a sample epoch will produce a spatial LT that will be diffuse across locations, whereas a neuron that fires only with neurons that encode a specific segment of the maze will produce an LT that represents that same segment. Critically, if the LT curve of a neuron learned from activity during an epoch does not match its maze place preference, then it cannot reasonably be said to ‘encode’ that same location during this epoch. The LT therefore allows us to examine for which time periods and which neurons we can use Bayesian decoding following more standard methods11,72.
This approach can be readily generalized to other neural systems for which tuning curves have been recorded, provided a sufficiently large number of units are recorded to sample the stimulus space. In the case of one-dimensional MAZE locations and PFs, we find that >40 simultaneously recorded units are needed to reliably obtain high-fidelity PFs (Extended Data Fig. 1). For larger or multiple environments, a greater number of units may be needed, as insufficient neuronal sampling or inherent preferences in the dataset (for example, for reward locations) may result in some biases across the stimulus space. Significance testing should therefore be carried out against unit-identity shuffles across available units. Before evaluating offline LTs, validation can be carried out against online data to confirm adequate sampling resolution.
Additional restrictions to avoid potential confounds from unit waveform clustering
To avoid potential confounds from spike misclassification of units detected on the same shank73, we applied additional inclusion requirements for LT calculations. We determined the L ratios74 between unit \(i\) and each other unit recorded on the same shank, yielding the cumulative probability of the other units’ spikes belonging to unit \(i\). As the range of L ratio depends on the number of included channels, to provide a consistent threshold for all datasets, the L ratio for each pair was calculated using the four channels that featured the highest spike amplitude difference between each pair of units. Only units with L ratio > 10−3 (Extended Data Fig. 3) were used to calculate LTs for each cell.
Fidelity of the LTs across epochs
To quantify the degree to which tuning curves in LTs or PFs relate across epochs, we used a simple Pearson correlation coefficient across position bins. We obtained consistent results with the Kullback–Leibler divergence (not shown). The median for each epoch was compared against a surrogate distribution of such median values obtained by shuffling (104 times) the unit identities of the PFs within each session. Thus, we tested against the null hypothesis that LTs in each session may have trivial non-zero correlations with PFs. For each epoch we obtained P values based on the number of such surrogate median values that were greater than or equal to those in the original data. With the exception of the analysis in Fig. 2, only units that participated in >100 ripple events in PRE or POST were included in the analysis.
LT stability and dynamics
We further evaluated the dynamics of LTs across time in non-overlapping 15-min windows (except for illustration purposes alone, in time-evolved LTs in Figs. 3a, 4a and 5h and Extended Data Fig. 3, in which we used overlapping 15-min windows with a 5-min step size). A unit’s LT stability was defined as the median Pearson correlation coefficient between that unit’s LTs in all different pairs of time windows within a given epoch. Thus, units that had stable and consistent LTs across an epoch yield higher correlations in these comparisons than those with unstable LTs. These unit LT stability values were z-scored against a null distribution of median correlation coefficients based on randomizing the LTs’ unit identities within each 15-min time window (1,000 shuffles). Normalized stability correlation matrices in Fig. 4c were calculated by z-scoring each correlation coefficient against a surrogate distribution based on shuffling the LTs’ unit identities. To investigate the changes in POST LT stability over time in Fig. 4c, we calculated LT stability within overlapping 2-h blocks with a step size of 1 h.
Ripple event replay scores
The posterior probability matrix (\(P\)) for each ripple event was calculated on the basis of previously published methods. Replays were scored using the absolute weighted correlation between decoded position (\(x\)) and time bin (\(t\))36:
in which \(i\) and \(j\) are time bin and position bin indices, respectively, and
Each replay score was further quantified as a percentile relative to surrogate distributions obtained by shuffling the data according to the commonly used within-event time swap, in which time bins are randomized within each ripple event72. We preferred this method over the circular spatial bin shuffle (or column-cycle shuffle72) as it preserves the distribution of peak locations across time bins within each event (see also related discussion in ref. 33). Each ripple event was assigned to one of four quartiles on the basis of the percentile score of the corresponding replay relative to shuffles.
PF overlap with decoded posterior
For the analysis displayed in Extended Data Fig. 4, a Pearson correlation coefficient was calculated between the PF of each unit firing (participating) in a time bin and the posterior probability distribution for that bin based on the firings of all units. The mean posterior correlation of PFs was calculated over all participating units. As this mean posterior correlation might be inflated when there is a low number of active units, for each time bin with \(n\) participating units we generated a surrogate distribution of mean posterior correlation by randomly selecting \(n\) units from the population recorded in that session. Then, the mean posterior correlation in the original data was z-scored against the corresponding surrogate distribution for \(n\).
θ-oscillation LT variations with oscillation characteristics
We investigated how LTs during periods dominated by θ-oscillations, such as MAZE active running periods and REM periods, were influenced by oscillation characteristics, such as power, phase and frequency. θ-oscillation power was determined by computing the power spectrum of the LFP recorded from the channel exhibiting maximum ripple power (typically in the pyramidal layer) in 2-s windows with 1-s overlap, using the Chronux toolbox (version 2.12) and averaging the power within the θ-oscillation frequency range (5–10 Hz). θ-oscillation frequency within each window was identified as the frequency exhibiting peak power within the θ-oscillation frequency range. θ-oscillation phase was obtained by band-pass filtering the LFP within θ-oscillation frequency range and computing the phase of the analytic signal derived from the Hilbert transform of the θ-filtered LPF. θ-oscillation periods were divided into 20-ms time bins, and θ-oscillation power, frequency and phase were calculated within each bin using linear interpolation. Time bins were then categorized into low versus high θ-oscillation power or frequency according to the medians of the corresponding distributions across all time bins within each session. To compensate for potential misalignment between unit and LFP signals, we first aligned the instantaneous phase signal such that the θ-oscillation trough corresponded with maximum population firing across all units. Subsequently, time bins were divided into trough (−π/4–π/4), ascending (π/4–3π/4), peak (3π/4–5π/4) and descending (5π/4–7π/4) θ-phases. The LTs were calculated separately for each subset of phases, as depicted in Extended Data Figs. 2f and 7e. REM periods were restricted to intervals lasting at least 6 s to minimize false positives. For analyses of MAZE active running periods, θ-oscillation periods were restricted to intervals in which the animal’s velocity exceeded 10 cm s−1 and we matched the number of firing bins for each unit across all data splits to control for possible differences. LT variations with respect to animal’s velocity during MAZE periods were determined by calculating LTs for distinct subsets of time bins, divided according to the median of the velocity distribution across all MAZE θ-oscillation time bins within each session.
Multiple regression analyses
To examine the extent to which a spatial tuning curve (LT or PF) within a given epoch was affected by the tuning curves in other epochs, we carried out multiple regression analyses. For example, we modelled POST LTs using:
and reMAZE PFs using
The dependent variables and regressors were calculated over all position bins from all units. The average LT in the analyses was calculated by averaging all unit LTs over PRE and POST. The c-terms and β-terms are the regression coefficients.
To test the statistical significance of the regression \({R}^{2}\) values and each regression \(\beta \)-coefficient, we compared these against distributions of surrogates (104 shuffles) calculated by randomizing the unit identities of the dependent variable’s tuning curves. For each coefficient and \({R}^{2}\) value, we obtained a P value based on the number of surrogates that were greater than or equal to those in the original data.
Bayesian LT with uninformative prior
We will define \({s}_{\forall j\ne i}\) as the vector of spike observations for all neurons except the ith, and \({{s}_{\forall j\ne i}}^{t}\) is the observation at time \(t\). \(p(x| {s}_{\forall j\ne i})\) is the posterior probability distribution of positions as already defined (calculated using the firing rate estimates from PFs using a uniform prior over position).
Define our observations at time t, \({D}^{t}=[{{s}_{\forall j\ne i}}^{t}\,;{s}_{i}^{t}]\). Assume that the neuron of interest exhibits Poisson spiking over the spatial bins \({x}_{m}\), with parameter \({g}_{m}\); in other words, \(p({s}_{i}|x={x}_{m}) \sim {\rm{P}}{\rm{o}}{\rm{i}}{\rm{s}}{\rm{s}}{\rm{o}}{\rm{n}}({g}_{m})\), where ~ indicates ‘distributed as’. Thus, our estimation problem is specifically to find the best estimates of the m parameters, \(g=\{\,{g}_{m}\}\).
In general, the Bayesian data likelihood is found using the Bayes rule:
Thus, for all of our observations, we can write:
in which, in the last line, we have taken advantage of the conditional independence of the spiking \({s}_{1},\ldots ,{s}_{n}\,\) of the neurons in each time bin conditioned on the position \({x}^{t}\) in that bin, and the activity of the other neurons, on the parameters.
To find the best parameters, we will maximize the logarithm of this quantity by taking the derivative with respect to each \(g=\{\,{g}_{k}\}\) and setting it equal to zero.
We will assume that our neurons are Poisson distributed; that is:
Note that the derivative with respect to the parameter \({g}_{k}\) can be expressed as
Thus, we have:
To bias the results as little as possible, we will use a flat prior \(p\left({g}_{k}\right)=1\) for \({g}_{k} > 0\) (note that this is an ‘improper’ prior as it does not integrate to 1, but the posterior is still proper75). Another alternative might be to shape the parameter distribution using a conjugate prior with parameters determined using information from the behavioural period or from the statistics of the other neurons. With an uninformative prior,
Rearranging this, we write:
This can be interpreted as a normalized spike-triggered average posterior probability distribution over space, triggered on the spikes of the neuron whose LT we are calculating.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The Grosmark dataset is publicly available at https://doi.org/10.6080/K0862DC5. The Miyawaki and Giri datasets are available upon request from the corresponding author.
Code availability
Custom-written MATLAB and python code supporting this study is available at https://github.com/diba-lab/Maboudi_et_al_2022.
References
Mankin, E. A. et al. Neuronal code for extended time in the hippocampus. Proc. Natl Acad. Sci. USA 109, 19462–19467 (2012).
Klinzing, J. G., Niethard, N. & Born, J. Mechanisms of systems memory consolidation during sleep. Nat. Neurosci. 22, 1598–1610 (2019).
Havekes, R. & Abel, T. The tired hippocampus: the molecular impact of sleep deprivation on hippocampal function. Curr. Opin. Neurobiol. 44, 13–19 (2017).
Hebb, D. O. The Organization of Behavior (Wiley, 1949).
O’Keefe, J. & Dostrovsky, J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 34, 171–175 (1971).
Zhang, K., Ginzburg, I., McNaughton, B. L. & Sejnowski, T. J. Interpreting neuronal population activity by reconstruction: unified framework with application to hippocampal place cells. J. Neurophysiol. 79, 1017–1044 (1998).
Frank, L. M., Stanley, G. B. & Brown, E. N. Hippocampal plasticity across multiple days of exposure to novel environments. J. Neurosci. 24, 7681–7689 (2004).
Dong, C., Madar, A. D. & Sheffield, M. E. J. Distinct place cell dynamics in CA1 and CA3 encode experience in new environments. Nat. Commun. 12, 2977 (2021).
Alme, C. B. et al. Place cells in the hippocampus: eleven maps for eleven rooms. Proc. Natl Acad. Sci. USA 111, 18428–18435 (2014).
Ziv, Y. et al. Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 16, 264–266 (2013).
van der Meer, M. A. A., Kemere, C. & Diba, K. Progress and issues in second-order analysis of hippocampal replay. Philos. Trans. R. Soc. B 375, 20190238 (2020).
Dragoi, G. & Tonegawa, S. Preplay of future place cell sequences by hippocampal cellular assemblies. Nature 469, 397–401 (2011).
Cirelli, C. & Tononi, G. The why and how of sleep-dependent synaptic down-selection. Semin. Cell Dev. Biol. 125, 91–100 (2022).
Giri, B., Miyawaki, H., Mizuseki, K., Cheng, S. & Diba, K. Hippocampal reactivation extends for several hours following novel experience. J. Neurosci. 39, 866–875 (2019).
Grosmark, A. D., Sparks, F. T., Davis, M. J. & Losonczy, A. Reactivation predicts the consolidation of unbiased long-term cognitive maps. Nat. Neurosci. 24, 1574–1585 (2021).
Pettit, N. L., Yap, E. L., Greenberg, M. E. & Harvey, C. D. Fos ensembles encode and shape stable spatial maps in the hippocampus. Nature 609, 327–334 (2022).
Wiskott, L. Lecture Notes on Bayesian Theory and Graphical Models. Institut für Neuroinformatik https://www.ini.rub.de/PEOPLE/wiskott/Teaching/Material/Bayes-LectureNotesPublicVideoAnnotated.pdf (2013).
Diba, K. & Buzsaki, G. Forward and reverse hippocampal place-cell sequences during ripples. Nat. Neurosci. 10, 1241–1242 (2007).
Dragoi, G. & Buzsaki, G. Temporal encoding of place sequences by hippocampal cell assemblies. Neuron 50, 145–157 (2006).
Tirole, M., Huelin Gorriz, M., Takigawa, M., Kukovska, L. & Bendor, D. Experience-driven rate modulation is reinstated during hippocampal replay. eLife 11, e79031 (2022).
Siclari, F. et al. The neural correlates of dreaming. Nat. Neurosci. 20, 872–878 (2017).
Vertes, R. P. Memory consolidation in sleep; dream or reality. Neuron 44, 135–148 (2004).
Miyawaki, H. & Diba, K. Regulation of hippocampal firing by network oscillations during sleep. Curr. Biol. 26, 893–902 (2016).
Norimoto, H. et al. Hippocampal ripples down-regulate synapses. Science 359, 1524–1527 (2018).
Kinsky, N. R., Sullivan, D. W., Mau, W., Hasselmo, M. E. & Eichenbaum, H. B. Hippocampal place fields maintain a coherent and flexible map across long timescales. Curr. Biol. 28, 3578–3588 (2018).
Geva, N., Deitch, D., Rubin, A. & Ziv, Y. Time and experience differentially affect distinct aspects of hippocampal representational drift. Neuron 111, 2357–2366 (2023).
Khatib, D. et al. Active experience, not time, determines within-day representational drift in dorsal CA1. Neuron 111, 2348–2356 (2023).
Drieu, C., Todorova, R. & Zugaro, M. Nested sequences of hippocampal assemblies during behavior support subsequent sleep replay. Science 362, 675–679 (2018).
Liu, C., Todorova, R., Tang, W., Oliva, A. & Fernandez-Ruiz, A. Associative and predictive hippocampal codes support memory-guided behaviors. Science 382, eadi8237 (2023).
Roux, L., Hu, B., Eichler, R., Stark, E. & Buzsaki, G. Sharp wave ripples during learning stabilize the hippocampal spatial map. Nat. Neurosci. 20, 845–853 (2017).
Yagi, S., Igata, H., Ikegaya, Y. & Sasaki, T. Awake hippocampal synchronous events are incorporated into offline neuronal reactivation. Cell Rep. 42, 112871 (2023).
Liu, K., Sibille, J. & Dragoi, G. Preconfigured patterns are the primary driver of offline multi-neuronal sequence replay. Hippocampus 29, 275–283 (2019).
Farooq, U., Sibille, J., Liu, K. & Dragoi, G. Strengthened temporal coordination within pre-existing sequential cell assemblies supports trajectory replay. Neuron 103, 719–733 (2019).
Grosmark, A. D. & Buzsaki, G. Diversity in neural firing dynamics supports both rigid and learned hippocampal sequences. Science 351, 1440–1443 (2016).
Foster, D. J. Replay comes of age. Annu. Rev. Neurosci. 40, 581–602 (2017).
Silva, D., Feng, T. & Foster, D. J. Trajectory events across hippocampal place cells require previous experience. Nat. Neurosci. 18, 1772–1779 (2015).
Hasselmo, M. E. What is the function of hippocampal theta rhythm?–Linking behavioral data to phasic properties of field potential and unit recording data. Hippocampus 15, 936–949 (2005).
Siegle, J. H. & Wilson, M. A. Enhancement of encoding and retrieval functions through theta phase-specific manipulation of hippocampus. eLife 3, e03061 (2014).
Ujfalussy, B. B. & Orban, G. Sampling motion trajectories during hippocampal theta sequences. eLife 11, e74058 (2022).
Olypher, A. V., Lansky, P. & Fenton, A. A. Properties of the extra-positional signal in hippocampal place cell discharge derived from the overdispersion in location-specific firing. Neuroscience 111, 553–566 (2002).
Monaco, J. D., Rao, G., Roth, E. D. & Knierim, J. J. Attentive scanning behavior drives one-trial potentiation of hippocampal place fields. Nat. Neurosci. 17, 725–731 (2014).
Gupta, A. S., van der Meer, M. A., Touretzky, D. S. & Redish, A. D. Hippocampal replay is not a simple function of experience. Neuron 65, 695–705 (2010).
Mattar, M. G. & Daw, N. D. Prioritized memory access explains planning and hippocampal replay. Nat. Neurosci. 21, 1609–1617 (2018).
Cheng, S. & Frank, L. M. New experiences enhance coordinated neural activity in the hippocampus. Neuron 57, 303–313 (2008).
Wilson, M. A. & McNaughton, B. L. Reactivation of hippocampal ensemble memories during sleep. Science 265, 676–679 (1994).
Bittner, K. C., Milstein, A. D., Grienberger, C., Romani, S. & Magee, J. C. Behavioral time scale synaptic plasticity underlies CA1 place fields. Science 357, 1033–1036 (2017).
Geiller, T. et al. Local circuit amplification of spatial selectivity in the hippocampus. Nature 601, 105–109 (2022).
Vaidya, S. P., Chitwood, R. A. & Magee, J. C. The formation of an expanding memory representation in the hippocampus. Preprint at bioRxiv https://www.biorxiv.org/content/10.1101/2023.02.01.526663v1 (2023).
Tingley, D. & Peyrache, A. On the methods for reactivation and replay analysis. Philos. Trans. R. Soc. B 375, 20190231 (2020).
Krause, E. L. & Drugowitsch, J. A large majority of awake hippocampal sharp-wave ripples feature spatial trajectories with momentum. Neuron 110, 722–733 (2022).
Stella, F., Baracskay, P., O’Neill, J. & Csicsvari, J. Hippocampal reactivation of random trajectories resembling Brownian diffusion. Neuron 102, 450–461 (2019).
Diba, K. Hippocampal sharp-wave ripples in cognitive map maintenance versus episodic simulation. Neuron 109, 3071–3074 (2021).
Genzel, L., Kroes, M. C., Dresler, M. & Battaglia, F. P. Light sleep versus slow wave sleep in memory consolidation: a question of global versus local processes? Trends Neurosci. 37, 10–19 (2014).
Poe, G. R., Nitz, D. A., McNaughton, B. L. & Barnes, C. A. Experience-dependent phase-reversal of hippocampal neuron firing during REM sleep. Brain Res. 855, 176–180 (2000).
Zielinski, M. C., Shin, J. D. & Jadhav, S. P. Hippocampal theta sequences in REM sleep during spatial learning. Preprint at bioRxiv https://www.biorxiv.org/content/10.1101/2021.04.15.439854v1.full (2021).
Louie, K. & Wilson, M. A. Temporally structured replay of awake hippocampal ensemble activity during rapid eye movement sleep. Neuron 29, 145–156 (2001).
Boyce, R., Glasgow, S. D., Williams, S. & Adamantidis, A. Causal evidence for the role of REM sleep theta rhythm in contextual memory consolidation. Science 352, 812–816 (2016).
Hobson, J. A. REM sleep and dreaming: towards a theory of protoconsciousness. Nat. Rev. Neurosci. 10, 803–813 (2009).
Colgin, L. L., Kubota, D., Jia, Y., Rex, C. S. & Lynch, G. Long-term potentiation is impaired in rat hippocampal slices that produce spontaneous sharp waves. J. Physiol. 558, 953–961 (2004).
Schacter, D. L., Addis, D. R. & Buckner, R. L. Episodic simulation of future events: concepts, data, and applications. Ann. N. Y. Acad. Sci. 1124, 39–60 (2008).
Siegle, J. H. et al. Open Ephys: an open-source, plugin-based platform for multichannel electrophysiology. J. Neural Eng. 14, 045003 (2017).
Yger, P. et al. A spike sorting toolbox for up to thousands of electrodes validated with ground truth recordings in vitro and in vivo. eLife 7, e34518 (2018).
Rossant, C. et al. Spike sorting for large, dense electrode arrays. Nat. Neurosci. 19, 634–641 (2016).
Bartho, P. et al. Characterization of neocortical principal cells and interneurons by network interactions and extracellular features. J. Neurophysiol. 92, 600–608 (2004).
Petersen, P. C., Siegle, J. H., Steinmetz, N. A., Mahallati, S. & Buzsaki, G. CellExplorer: a framework for visualizing and characterizing single neurons. Neuron 109, 3594–3608 (2021).
Grosmark, A. D., Long, J. D. & Buzsáki, G. Recordings from hippocampal area CA1, PRE, during and POST novel spatial learning. CRCNS.org https://doi.org/10.6080/K0862DC5 (2016).
Skaggs, W., McNaughton, B. & Gothard, K. An information-theoretic approach to deciphering the hippocampal code. In Advances in Neural Information Processing Systems 5 (eds Hanson, S., Cowan, J. & Giles, C.) 1030–1037 (Morgan Kaufmann Publishers Inc., 1992).
Wen, H. & Liu, Z. Separating fractal and oscillatory components in the power spectrum of neurophysiological signal. Brain Topogr. 29, 13–26 (2016).
Bokil, H., Andrews, P., Kulkarni, J. E., Mehta, S. & Mitra, P. P. Chronux: a platform for analyzing neural signals. J. Neurosci. Methods 192, 146–151 (2010).
Buzsaki, G. Theta oscillations in the hippocampus. Neuron 33, 325–340 (2002).
Park, M., Weller, J. P., Horwitz, G. D. & Pillow, J. W. Bayesian active learning of neural firing rate maps with transformed Gaussian process priors. Neural Comput. 26, 1519–1541 (2014).
Davidson, T. J., Kloosterman, F. & Wilson, M. A. Hippocampal replay of extended experience. Neuron 63, 497–507 (2009).
Quirk, M. C. & Wilson, M. A. Interaction between spike waveform classification and temporal sequence detection. J. Neurosci. Methods 94, 41–52 (1999).
Schmitzer-Torbert, N., Jackson, J., Henze, D., Harris, K. & Redish, A. D. Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience 131, 1–11 (2005).
Murphy, K. P. Machine Learning: a Probabilistic Perspective (MIT Press, 2012).
Acknowledgements
We thank A. Amarasingham, T. Abel, G. Mashour, M. van der Meer, N. Kinsky, P. Hale and R. Wahlberg for comments on the manuscript. This work was financed by the US National Institute of Neurological Disorders and Stroke (R01NS115233) and the US National Institute of Mental Health (R01MH117964).
Author information
Authors and Affiliations
Contributions
K.D. and K.M. conceived the analytical approach. B.G. conceived and carried out sleep and reMAZE experiments for the Giri dataset. H.M. carried out maze and sleep recordings for the Miyawaki dataset. K.M. carried out all analyses. K.D. supervised the research with input from C.K. K.D. and K.M. wrote the manuscript with input from C.K. and H.M.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Antonio Fernandez-Ruiz, John Widloski and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 The factors that impact learned tunings.
In three sample maze sessions we calculated LTs by (a) randomly varying the number and subset of awake ripple events, or (b), varying the number of units included, and tested the effects on the quality of LTs, as reflected by PF fidelity. Samples that yielded with significant median LT fidelities (r(LT, PF), p < 0.01 relative to unit ID shuffle) are represented in gray dots, whereas non-significant samples are indicated by empty circular markers. The median LT fidelity increases as more ripples and units are incorporated. Based on these results, we estimate that approximately 40 simultaneously recorded units are needed to obtain quality LTs, whereas the minimum number of ripples could vary across sessions, with as few as five ripples needed to generate LTs with significant PF fidelities in some cases. (c) The distribution of PF fidelities corresponding to quiet wake (QW), or slow-wave sleep (SWS), when the number of firing time bins utilized for calculation of each unit’s LT were matched between PRE and POST via subsampling the firing time bins, indicated significant difference between PRE and POST within each event category (QW: P = 2.0 × 10−35; SWS: P = 2.7 × 10−43, two-sided Wilcoxon signed-rank tests with no correction for multiple comparisons). (d) Left, the distribution of the mean sharpness of the posterior probability distribution over position (quantified by the Gini coefficient, see Methods) used in LT calculations for units in each event category. There was a significant effect of event category (p = 1.5 × 10−151, Friedman’s test) with both QW and SWS had higher median Gini coefficients (i.e. sharper posteriors) than REM (QW versus REM: P < 4.3 × 10−98; SWS versus REM: P = 3.8 × 10−97, two-sided WSRT with no correction for multiple comparisons). The overlaid lines (dots for sessions with no REM in PRE) connect median values corresponding to individual sessions. PRE and POST also exhibited slightly different Gini coefficients during QW (P = 5.0 × 10−11) or REM (P = 8.6 × 10−11) but not during SWS (P = 0.95), though the effect sizes of the difference were small (QW: 0.20; SWS: 0.04; REM: −0.29). Right, the correlation between the PF fidelity and posterior Gini coefficient for PRE (top) and POST (bottom) by pooling across all event categories (best linear fits in black with 95% confidence intervals in shaded gray) was weak in both PRE and POST, and significant during POST (P = 0.004) but not PRE (P = 0.72), indicating that the sharpness of posteriors was not a major driver of differences between PRE and POST LTs. (e) The distributions of the number of bins with spikes used to calculate LTs in QW ripples, SWS ripples, and REM sleep during PRE or POST epochs in Fig. 2a. The overlaid lines (dots for sessions with no REM in PRE) connect median values corresponding to individual sessions. (f) The distributions of the average number of units that cofired with the learning unit when calculating LTs during each epoch. (g) Population vector correlation matrices (top) and cumulative distributions of PF fidelity (bottom) for SWS and QW LTs during POST, recalculated following subsampling of each unit’s SWS and QW firing bins to match the number of firing bins during the corresponding REM periods.
Extended Data Fig. 2 The impact of sleep oscillations on LT quality.
(a) Top row, the fraction of each sleep state in 2-minute sliding windows during POST from a sample session. Middle row, the power of δ-oscillations (1–4 Hz) in 2-second sliding windows (gray) across POST. Filled and empty dots indicating SWS ripple events with high (≥ median) or low (< median) δ-oscillation power for that session. Bottom row, similar to the middle panel, but for spindle power (9–18 Hz) calculated in 500 ms sliding windows (gray). (b) In POST, but not PRE, SWS ripples separated into those occurring during high vs. low δ-oscillation power (left) and high vs. low spindle power (middle) resulted in higher fidelity when the oscillations were present at higher power. When we split each 2-s δ-oscillation window into two 500 ms windows with higher and two 500 ms windows with lower spindle power, to isolate the impact of spindles at each level of δ-oscillation power, we observed higher fidelity LTs for ripples that occurred during the high spindle power subset. (c) LTs calculated based on events with high (≥ median) ripple (120–250 Hz) amplitude, multi-unit firing rate, unit participation rate, or ripple event duration, all exhibited significantly higher PF fidelity compared to those with low (< median) values in POST. In all comparisons in (b) and (c), LTs were calculated based on matched number of bins and p-values (inset) were derived from Wilcoxon signed-rank tests. (d) Distributions of the duration of ripple events obtained from each session in each dataset. (e) The distribution of θ-oscillation amplitude (z-scored over REM, left) and frequency (right) during the REM periods in POST (n = 813613 20-ms time bins pooled across all sessions), with individual session medians (dots) and interquartile ranges (horizontal lines) superimposed. (f) PF fidelity of LTs in POST REM calculated based on distinct subsets of 20-ms time bins separated according to high and low θ-oscillation amplitude (left panel) or frequency (middle panel) separated by the median values in each session. There was a significant effect of frequency (p = 0.02, two-sided WSRT, n = 660). Similarly, REM LTs calculated based on separating windows according to θ phase (right panel) into trough (−π/4 – π/4), ascending (π/4 – 3π/4), peak (3π/4 – 5π/4) and descending (5π/4-7π/4) phase. Median PF fidelities significantly differed across θ phase (P = 0.0015, Friedman’s test, n = 660) (g) We tested the effect of different sized time bins on REM LT-PF fidelities in PRE (left) and POST (right). While the effect was subtle and not significantly different across different sized bins (Friedman’s test), LTs using 125 ms and 250 ms bin durations exhibited significantly aligned LT-PF fidelities (median fidelities compared (one-sided) to null distributions obtained from 104 unit identity shuffles without multiple comparison corrections). (h) The posteriors used to calculate LTs exhibit greater sparsity for larger bin sizes in both PRE and POST REM. This is because larger bins result in more active neurons within each bin, producing increasingly sharper posteriors (see equation (9), Methods).
Extended Data Fig. 3 Additional examples of the evolution of LTs from PRE to POST.
Similar to Fig. 3a, heat maps of ripple LTs in sliding 15 min windows from PRE through MAZE to POST (maze place fields in gray on right) for 6 sample units from each of 5 different sessions (hypnogram on top left indicating the brain state, quiet wake (QW), active wake (AW), rapid eye movement (REM) sleep, and slow-wave sleep (SWS) at each timepoint).
Extended Data Fig. 4 Place field fidelities do not strictly correlate with replay score.
(a) Distribution of replay scores in the different datasets calculating as percentile against time shuffled bins. Median scores for different epochs are shown with dashed lines (chance median score = 50; see Methods). (b) Ripple events were divided into quartiles according to replay score. Top panels show the place fields and sets of LTs calculated based on low and high quartile replay score events within PRE, MAZE, and POST. Bottom panels show population vector (PV) correlations between position bins in the PFs versus different sets of LTs. (c) Distribution of PF fidelity for each ripple subset. Median PF fidelities were significantly greater compared (one-sided) against surrogate distributions (from 104 unit identity shuffles, without multiple comparison corrections) in all subsets during MAZE and POST but not during PRE (PRE; P = 0.86, P = 0.67, P = 0.49, P = 0.06 for first to forth quartiles, respectively. MAZE and POST: P < 10−4 for all quartiles). (d) Place fields of participating units in replays show differing amounts of overlap with the decoded posteriors. Example events with high replay scores in PRE and POST, and low replay scores in POST showing posterior probability matrices and corresponding spike rasters of units sorted by place field order. The middle row depicts the mean correlation of the participating units’ place fields with the decoding posterior in each time bin. The bottom panels show the place fields and decoded positions of participating units for example time bins. Note that even bins with poor place-field coherence display sharp posteriors, because of the multiplication rule in Bayes formula, whereby spatial tunings of participating units are multiplied by each other. (e) Mean posterior correlation of PFs and decoded positions show increased place-field overlap in both low and high score replays in POST compared to PRE. Low and high replay score events in PRE did not differ significantly (PRE low versus high: P = 0.36; POST low versus high: P = 1.8 × 10−66; POST high versus PRE high: P = 1.1 × 10−282; POST low versus PRE high: P = 1.1 × 10−59; two-sided Mann Whitney U Test). ***P < 0.001.
Extended Data Fig. 5 Additional details and variations on MAZE/reMAZE analyses.
(a) Place fields (PFs) from MAZE and reMAZE for all units used for analyses in Fig. 5. (b) PF peak firing rates during MAZE and reMAZE and their marginal histograms. Despite an apparent modest decrease in peak firing rates during reMAZE and disappearance or appearance of a small subset of units (orange dots), peak firing rates in reMAZE and MAZE remained significantly correlated. In this and subsequent panels, best linear fit and 95% confidence intervals are overlaid with black line and shaded gray, respectively. (c) The same as (b) but for spatial information between MAZE and reMAZE spatial tunings across units. (d). POST LT fidelity to MAZE PFs (left) is correlated with the similarity to the reMAZE PF. Likewise, POST LT similarity to reMAZE PFs (right) is correlated with the similarity between MAZE and reMAZE PFs. (e) MAZE/reMAZE similarity correlation with POST PF fidelity (as in Fig. 5f) separately for units with lower (left) or higher (right) PF stabilities relative to each session’s median. Higher POST fidelity was predictive of greater MAZE/reMAZE similarity in both sets. (f) Multiple regression separately for each panel directly above in (e) The regressors were more predictive (higher R2) for units with more stable MAZE PFs, but POST LTs beta coefficients were similar between units with lower or higher PF stabilities (both p values = 0.02). P values were obtained by comparing (one-sided) the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of reMAZE PFs. (g) PF fidelities of POST LTs calculated exclusively based on slow-wave sleep (SWS; left) or quiet wake (QW; right) ripple events both predicted similarity between MAZE and reMAZE place fields. However, a stronger correlation was observed for SWS LTs. (h) The same multiple regression analysis for modeling reMAZE PFs as in Fig. 5g but with the inclusion of POST SWS LTs (left panel), POST QW LTs (middle panel), or both (right panel), as regressors. While both SWS and QW POST LTs were predictive of reMAZE (P < 10−4 and P < 0.01, P values obtained by comparing (one-sided) the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of reMAZE PFs), the POST SWS LTs offered the stronger prediction. (i) The Gini coefficients of POST LT’s (measuring sparsity, i.e. sharpness of tuning) were significantly correlated with their similarity to reMAZE place fields. This demonstrates that sparser (as opposed to more diffuse) POST LTs display higher similarity with the upcoming place fields during maze re-exposure. (j) Similar to Fig. 5f & 5g, but using tunings learned during θ-oscillations (active periods) on MAZE and reMAZE. This analysis also allowed us to add data from an additional session (from Rat S) for which video tracking was lost during the reMAZE epoch). Left panel, the similarity of POST LTs with MAZE θ-oscillation LTs predicted the similarity between MAZE and reMAZE θ-oscillation LTs. Right panel, POST LTs remained predictive of reMAZE θ-oscillation LTs in this control comparison. (k) The stability of POST LTs (z-scored against unit-id shuffles, as in Fig. 3d) for units with MAZE PF peak firing rate < 1 Hz (threshold used in this paper) were not significantly > 0. (l) In the same set of units, the POST LTs did not display a significant correlation with reMAZE PFs (left) but still showed a significant correlation with reMAZE θ-oscillation LTs (right). (m) The correlation with reMAZE θ-oscillation LT was absent for latePOST LTs. (n) Multiple regression analyses for modeling the reMAZE PFs (left) or reMAZE θ-oscillation LTs (right) for these low-firing units both resulted in significant regression coefficients for POST LTs. *P < 0.05, **P < 0.01, ***P < 0.001.
Extended Data Fig. 6 Additional examples of the evolution of LTs from PRE to reMAZE.
Similar to Fig. 5h, heat maps of ripple LTs in sliding 15 min windows from PRE through MAZE, POST, and latePOST for sample units from 4 different sessions (hypnogram on top left indicate the brain state, quiet wake (QW), active wake (AW), rapid eye movement (REM) sleep, and slow-wave sleep (SWS) at each timepoint). MAZE and reMAZE place fields and LTs during PRE, POST, and latePOST are plotted on the right of each panel, except for Rat S for which we plot reMAZE θ-oscillation LTs (rather than reMAZE PFs) because video tracking was lost during reMAZE for this session.
Extended Data Fig. 7 The correlation between the learned tuning of units and their intrinsic and MAZE tuning properties.
(a) Left, the distribution of locations of peak tuning across POST ripple LTs and maze place field (PFs; best linear fit in black with 95% confidence intervals in shaded gray). Right, the marginal distributions of peak locations relative to the center of the track show similar distributions between POST LTs (top) and PFs (bottom). (b) Relationship between PF features and stability and fidelity of the POST LTs. First row, distribution of each MAZE spatial tuning metric by pooling units across all sessions (n = 660 units). The median and interquartile ranges corresponding to individual sessions are depicted using overlaid lines. To analyze the connection between the POST stability and fidelity with each MAZE spatial tuning metric, the set of units within each session was divided into low or high categories according to the median. Among the spatial tuning metrics, peak place field firing rate (peak PF FR), and PF stability were predictive of the POST LT fidelity and stability. We saw no effect from metrics such as spatial information or PF distance from the track center. Cross-group comparisons used two-sided Mann Whitney U Tests. (c) Similar analysis on unit firing characteristics indicates that firing burstiness is not a factor driving LT stability or fidelity. Additionally, higher firing rates during the POST ripples affected the stability of POST LTs but not their fidelity. Median and interquartile ranges corresponding to individual sessions are superimposed with colored dots and lines. Cross-group comparisons used two-sided Mann Whitney U Tests. (d) The distribution of θ-oscillation amplitude (z-scored), frequency, and velocity of the animal observed during MAZE theta periods for a sample session (top row) and for overall distributions (bottom row) by pooling over all sessions (n = 2250347 20-ms time bins). Median and interquartile ranges corresponding to individual sessions are superimposed with colored dots and lines. (e) From left to right, PF fidelity of MAZE θ-oscillation LTs calculated based on distinct subsets of 20-ms time bins into Low/High relative to session medians showed significant effects for theta amplitude (1st column) (P = 0.01) or frequency (2nd column) (P = 7.9 × 10−16). The impact of θ phase (3rd column) on MAZE θ-oscillation LTs was investigated by calculating the LTs based on distinct set of 20-ms time bins according to θ-oscillation phase: Trough (−π/4 to π/4), Ascend (π/4 to 3π/4), Peak (3π/4 to 5π/4), Descend (5π/4 to 7π/4). LTs associated with the trough and descending phase of theta displayed higher PF fidelity than other theta phases (cross-group comparison using Friedman’s test; P = 2.2 × 10−13 with post hoc comparisons within each pair; Trough vs. Ascend: P = 2.1 × 10−5; Trough vs. Peak: P = 2.2 × 10−12; Trough vs. Descend: P = 0.002; Ascend vs. Peak: P = 3.6 × 10−5; Ascend vs. Descend: P = 0.12; Peak vs. Descend: P = 9.2 × 10−8). θ-oscillation periods split according to the animal’s velocity (4th column) during the θ-oscillation periods (p = 6.7 × 10−18). These panels indicate significant differences compared to chance levels (vs. unit-ID shuffle surrogates) within each group, as well as comparisons across groups (two-sided Wilcoxon Signed-Rank Tests). (f) Multiple regression analysis revealed that learned tunings calculated based on firing during MAZE θ-wave trough, but not θ-wave peak, strongly predict POST learned tunings, along with MAZE ripple LTs (θ-wave peak LTs: P = 0.35; θ-wave trough, PRE, ripple LTs, and MAZE PFs: P < 10−4). P values were obtained by comparing (one-sided) the R2 and each coefficient against surrogate distributions from 104 unit-identity shuffles of POST LTs. Results obtained by leaving out individual sessions are superimposed with dots. *P < 0.05, **P < 0.01, ***P < 0.001.
Extended Data Fig. 8 Unit stability and isolation.
(a) Sample units (from Rat U) depicting mean spike waveform and unit stability assessed by spike amplitude, isolation distance, and firing rate over three sleep epochs (PRE, POST, and latePOST). Inclusion thresholds for isolation distance and firing rates are shown with dashed lines. (b) The distribution of unit stability measures by pooling across all units in sessions shown for each dataset. See Methods for further details on unit inclusion criteria. Within-group comparisons used two-sided Wilcoxon Signed Rank Tests. (c) The L-ratio was used to quantify the degree of overlap in the spike feature space between each pair of units. Each scatterplot (top row) shows the spikes of the reference unit #20 (black) and other units (colored) recorded on the same shank in an example recording session from the Giri dataset. The axes in each scatterplot correspond to the spike amplitude on two channels with maximal distinction between the pairs, showing a range of overlap with unit #20. For example, unit #30 on the leftmost inset showed almost no overlap, whereas unit 19 on the rightmost inset significantly overlapped. The L ratio (e.g. between unit #20 and the other units) was obtained by calculating the probability of spikes from the second unit belonging to the reference unit. An L ratio threshold of 10−3 was applied to include only isolated units for determining the LTs of each reference cell. Corresponding mean spike waveforms (bottom row) provided for each pair of units across recording electrodes. (d) The cumulative distributions of L ratios for this example session and across all sessions (top) (n = 40207 unit pairs). The L-ratios for each individual session (bottom), showing mean (dots), the full range (whiskers) and interquartile range (boxes).
Supplementary information
Supplementary Information
Supplementary text regarding representations during high-score preplays that do not align with maze PFs, Supplementary References and Tables 1–3.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Maboudi, K., Giri, B., Miyawaki, H. et al. Retuning of hippocampal representations during sleep. Nature 629, 630–638 (2024). https://doi.org/10.1038/s41586-024-07397-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-024-07397-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.